2019年高考全国Ⅰ卷理科第12题的解法分析及其题型归类

广东省湛江一中培才学校(524037) 魏 欣

2018年1月《普通高中数学课程标准(2017年版)》出版,正式公布了数学学科六大核心素养：数学抽象、逻辑推理、数学建模、直观想象、数学运算、数据分析.数学大师史宁中提出数学学科核心素养的本质就是“三会”：会用数学的眼光观察世界,会用数学的思维思考世界,会用数学的语言表达世界.

球相关的切、接问题,是近几年高考命题的热点,从“几何作图”和“分析图形”两个角度考查直观想象核心素养,考察考生的空间想象能力和逻辑思维能力,同时考查数学抽象、逻辑推理、数学建模、直观想象、数学运算的核心素养,也是考生的难点、易失分点.要解决这一难点,关键是找到反映“切、接”的几何量集中的一个截面,并找到这些几何量所满足的关系式.下面就2019年高考全国Ⅰ卷理科第12题进行详细分析、探究其规律,归类了近几年高考多面体与球的切接的问题,并给出其解题通法.

一、题目展示与分析

题目(2019年全国Ⅰ卷理科第12题)已知三棱锥P-ABC的四个顶点在球O的球面上,PA=PB=PC,△ABC是边长为2的正三角形,E,F分别是PA,AB的中点,∠CEF=90°,则球O的体积为( ).

图1

图2

分析本题以三棱锥与球的位置关系为问题背景,考查三棱锥的外接球的问题.利用相应线段的长度与角度的关系,确定三棱锥的准确信息,为进一步求解与应用提供条件.而结合两空间几何体的位置关系,可将此三棱锥不形成长方体入手,可以有效解决问题.

解析由题意,三棱锥P-ABC为正三棱锥.如图1,取AC中点D,连接PD,BD,则AC⊥PD,AC⊥BD,故AC⊥平面PBD,AC⊥PB.又 ∠CEF=90°,而PB//EF,故PB⊥CE.所以,PB⊥平面PAC,PB⊥PA,PB⊥PC.

由此可知,正三棱锥P-ABC的侧面为等腰直角三角形,且故此正三棱锥可视为棱长为的正方体的一角,如图2所示.设球O的半径为R,则,故球O的体积为

点评本题求解的关键步骤有二：一是认清三棱锥P-ABC的结构特征(也可以由cos∠AEC=-cos∠PEC及余弦定理列式计算得到侧棱长为故侧面为等腰直角三角形),二是通过构造正方体来求取外接球问题.事实上,当三棱锥某一顶点处的三条棱两两垂直时,可将此三棱锥补形成长方体,进而借助长方体的外接球来简化求解过程.

二、高考题分析

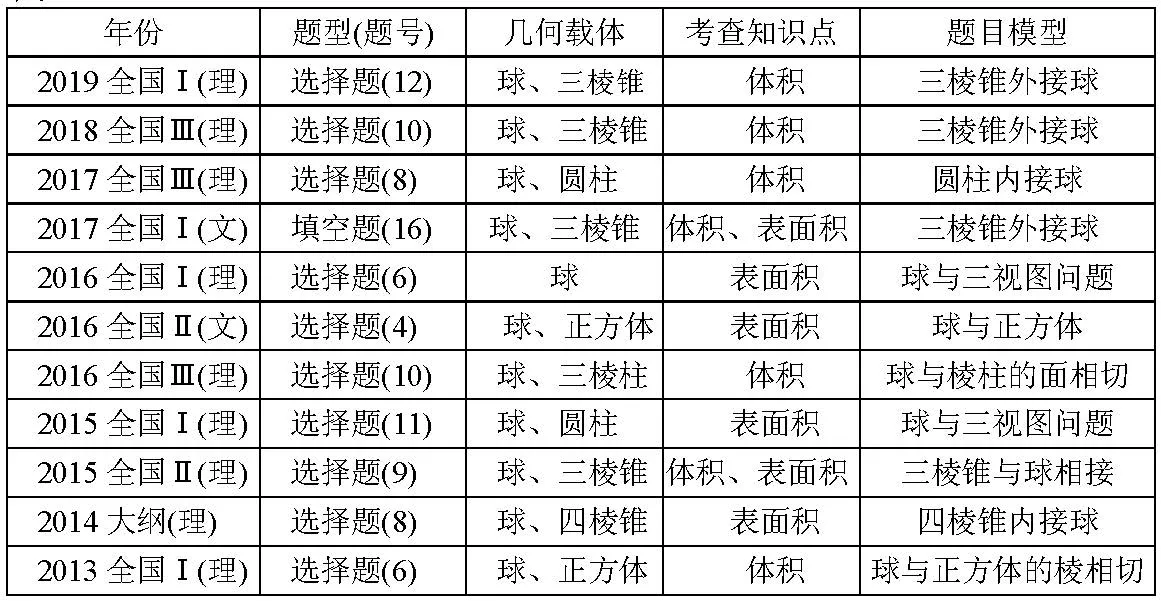
表1

与球相关的切、接问题,是近几年高考命题的热点,考察考生的空间想象能力和逻辑思维能力,也是考生的难点、易失分点,下面就近几年高考题对球与几何体的切接作深入的探究,从中掌握高考命题的趋势和高考的出题思路,使学生在这部分内容不失分.从近几年全国新课标高考命题来看,这部分内容主要出选择、填空题,命题角度多变,归纳起来常见的命题角度如表1.

从以上真题考查以下方面知识和能力：(1)与球相关的题目侧重考查学生的空间想象能力,对作图能力要求较高,要求学生必须能够作出直观图,然后利用直观图分析问题,学生要有较强的几何作图能力;(2)以截面问题为主,需选择恰当的截面解决问题,考查平面化的方法,考查化归与转化能力;(3)几何载体多变,以体积或表面积的计算为主,考查运算求解能力.下面就通过几个实例加以总结.

三、高考题型归类

题型一 正棱锥与球

性质正棱锥的外接球球心在正棱锥的高所在的直线上.

当棱锥的侧棱长相等时,棱锥顶点在底面上的射影是底面多边形的外心,而外接球球心与底面多边形外心的连线也与底面垂直,故外接球球心恰好在棱锥的高所在的直线上.

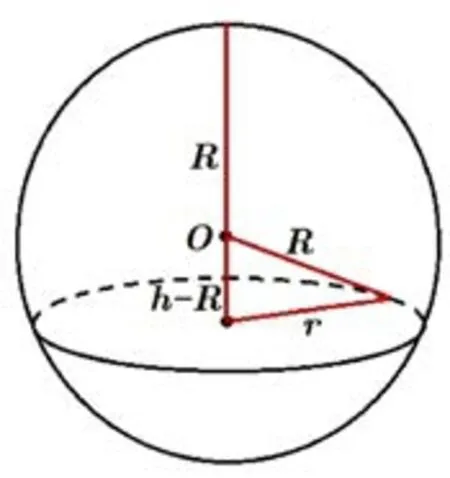
图3

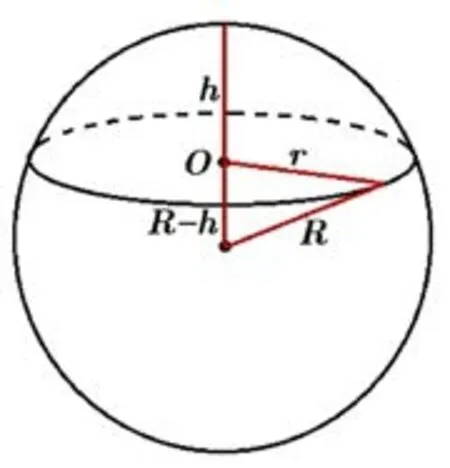
图4

如图3所示,若棱锥的侧棱长相等,且其高为h,底面外接圆半径为r,设其外接球半径为R(h≥R),根据勾股定理得同理,如下图4所示,当h＜R时,R2=(R-h)2+r2,也可得到所以,不论h与R的大小关系如何,总有

下面以正四面体为例说明.

正四面体放入正方体中,正方体的外接球的球心在其体对角线的中点上.设正四面体的棱长为a,正四面体的内切球、棱切球、外接球的半径分别为r1、r2、r3.过正四面体的一条棱及其对棱的中点可作包含各球基本量的截面,如图5所示,可知

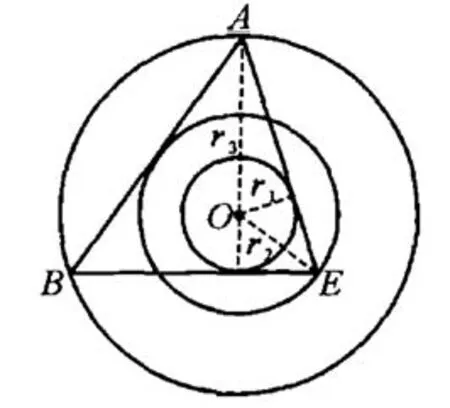
图5

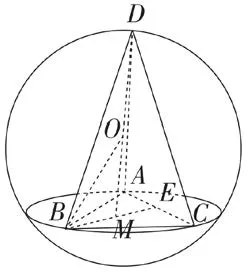
图6

例1(2018年全国ⅠⅠⅠ卷理科第10题)设A、B、C、D是同一个半径为4的球的球面上四点,△ABC为等边三角形且其面积为则三棱锥D-ABC体积的最大值为( ).

解析作图,D为MO与球的交点,点M为△ABC的重心.判断出当DM⊥平面ABC时,三棱锥D-ABC的体积最大,然后进行计算可得.

如图6所示,点M为△ABC的重心,E为AC的中点,当DM⊥平面ABC时,三棱锥D-ABC的体积最大,此时,OD=OB=R=4.因为所以AB=6.因为点M为△ABC的重心,所以所以在Rt△ABC中,有设球的半径为R,球心到等边△ABC的外接圆圆心的距离为d,则即OM=2.所以三棱锥D-ABC高的最大值为DM=OD+OM=4+2=6.所以所以三棱锥D-ABC体积的最大值为故选B.

题型二 正棱柱与球

性质正棱柱的上、下底面外心连线段的中点即为外接球球心.

下面以正三棱柱为例说明.

如图7所示,正三棱柱上、下底面外心连线段的中点即为外接球球心.在正三棱柱ABCA1B1C1中,设正三棱柱的高为h,底面外接圆半径为r,设其外接球半径为R(h≥R),根据勾股定理得,故外接球的半径

图7

例2(2019年大连一模理科第11题)已知三棱柱ABC-A1B1C1的六个顶点都在球O的球面上.若AB=3,AC=4,AB⊥AC,AA1=12,则球O的半径为( )

解析如图8,由球心作平面ABC的垂线,则垂足为BC的中点M.又所以球O的半径.故选C.

图8

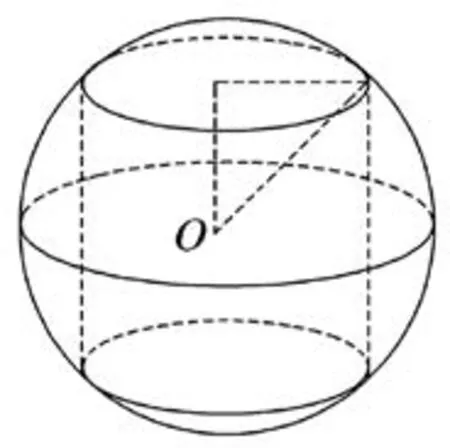
图9

例3(2017年高考全国ⅠⅠⅠ卷理科第8题)已知圆柱的高为1,它的两个底面的圆周在直径为2的同一个球的球面上,则该圆柱的体积为( ).

A.πB.C.D.

解析球与圆柱均是旋转体,由旋转体本身固有的对称性,我们重点研究轴截面,发现球的直径是圆柱轴截面矩形的对角线,由球心、底面圆心及底面圆上任意点构成的直角三角形,设底面圆半径为r,球的半径为,圆柱的高为h=1,如图9所示,由勾股定理得圆柱底面半径为

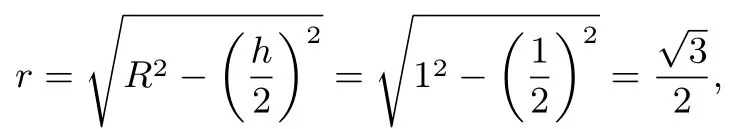
题型三 对棱相等模型

对棱相等模型采用的方法是补形为长方体.

例4(2016年高考全国ⅠⅠ卷文科第14题改编)正四面体的各条棱长都为则该正4面体外接球的体积为____.

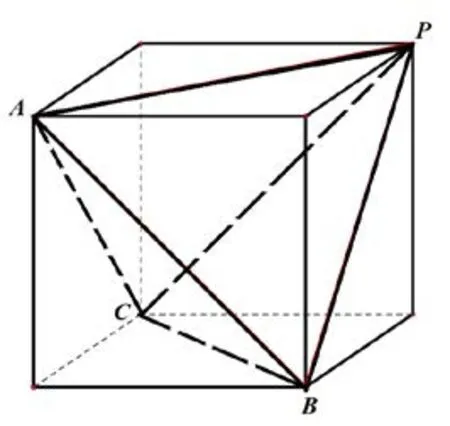
图10

解析如图10所示,正四面体对棱相等的模式,放入正方体中,正方体的外接球的球心与其体对角线的中点重合,所以.故填

题型四 折叠模型

例5(2019年厦门市一模)如图11,将边长为2的正△ABC沿着高AD,使∠BDC=60°,若折起后A、B、C、D四点都在球O的表面上,则球O的表面积为____.

图11

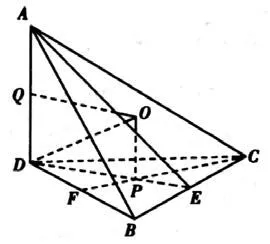
图12

解析折起后的几何体是如图12所示的三棱锥A-BCD,底面BCD是边长为1的正三角形,因为AD⊥DC,AD⊥DB,DC∩DB=D,DC、DB⊂底面BCD,所以AD⊥底面BCD.取棱BC、BD的中点E、F,连接DE、CF,交于点P,则点P为底面BCD的中心,过点P作底面BCD的垂线OP,取AD的中点Q,在平面ADE中作AD的垂直平分线交PO于点O,则点O为三棱锥外接球的球心,OD为半径,四边形POQD为矩形,且所以所以球O的表面积为.故填.

题型五 柱体的内切球问题

例6(2016年高考全国ⅠⅠⅠ卷文科第11题)在封闭的直三棱柱ABC-A1B1C1内有一个体积为V的球.若AB⊥BC,AB=6,BC=8,AA1=3,则V的最大值是( ).

A.4πB.C.6πD.

图13

解析根据题中的数据求半径,就转化成求三角形的内切圆的半径,如图13所示,这是初中的内容,运用等面积法可以求出其半径为2.这一问题有一易错点是求半径时还要考虑高,就是直径不能大于3,故直三棱柱ABC-A1B1C1的内切球的半径为,此时V的最大值是故选B.

四、备考建议

从上面的高考题型归类可以看处,球切接问题包含几种核心素养,下图是其对应的关系.

?

与球相关的题目在高考中主要以填选题的形式出现,侧重于考查学生的空间想象能力,要求颇高,从“分析图形”和“几何作图”两个不同的角度考查学生的核心素养.

在教学实践中,应注重多采用“举例”、“建模”、“类比”等方式对知识进一步整合,要强调经历从实际物体中抽象出空间几何体的过程,了解一些空间几何体和常见的平面图形;感受平移、旋转、轴对称图形还原等现象.在运用数及适当的度量单位描述现实生活中的空间几何体现象,以及对运算结果进行估计的过程中,发展数感;在从物体中抽象出几何图形、想象图形的运动和位置的过程中,发展空间观念.探索一些图形的形状、大小和位置关系,了解一些空间几何体和平面图形的基本特征;掌握识图、画图和求量的基本方法;形成数感和空间观念,感受符号和几何直观的作用.熟练掌握“补体法”、“分割法”、“等体积法”、“平面化方法”、添加各种辅助线等立体几何中的方法.从而提升学生的数学抽象、直观想象、数学建模、逻辑推理和数学运算的核心素养.