爆炸荷载在圆截面桥梁墩柱上的分布规律*

彭玉林，吴 昊，方 秦

（1. 陆军工程大学爆炸冲击防灾减灾国家重点实验室，江苏 南京 210007；2. 同济大学结构工程与防灾研究所，上海 200092）

随着全球地区冲突和恐怖主义事件不断加剧，大型标志性桥梁成为军事打击和恐怖袭击的潜在目标。据统计，在1980～2006 年之间全世界至少发生了53 起针对桥梁的恐怖袭击，其中60%为爆炸袭击[1]。图1 给出了爆炸荷载作用下由于墩柱丧失承载力而导致整个桥梁结构倒塌的事件[2-3]。现行桥梁设计考虑了车辆、地震、风荷载以及船舶撞击的偶然作用，然而未对桥梁结构在爆炸作用下的动力灾变能力和防护措施作出明确规定[4]。美国国家高速公路与交通运输协会发布了高速公路桥梁抗爆设计细则(NCHRP645)[5]，而国内对桥梁抗爆及防护的研究仍处于起步阶段。墩柱作为桥梁结构的主要受力构件，其在爆炸荷载作用下的损伤破坏直接影响到桥梁结构的稳定与安全。因此，本文选取桥梁墩柱作为桥梁抗爆研究的对象。

对于桥梁墩柱在爆炸荷载作用下的动态响应与破坏研究，Tang 等[6]和Hao 等[7]利用LS-DYNA 软件对斜拉桥桥墩等构件在不同位置爆炸荷载作用下的动力响应进行了数值模拟，分析了斜拉桥在爆炸作用下的破坏形态，并对CFRP 的加固效能进行了评价。Islam 等[8]通过数值计算分析了爆炸荷载下典型梁式桥桥墩的受力情况，并计算了不同桥梁构件(桥墩、桥面板等)破坏的最小TNT 当量。Winget 等[9]基于数值计算和单自由度理论模型分析指出，桥墩处爆炸时桥墩和桥面组合构成的密闭环境对爆炸冲击波具有增强效果。Williams 等[10]基于AASHTO LRFD 标准[11]设计了10 根不同构造的1/2 缩比钢筋混凝土桥梁墩柱模型，并开展了近距离(比例距离小于1.1 m/kg1/3)爆炸试验和数值模拟，分析了混凝土墩柱的破坏模式以及箍筋对核心混凝土的约束作用。Bruneau 等[12]考虑汽车炸弹的威胁，对带排架的1/4 缩比钢管混凝土墩柱模型进行了爆炸试验，结果表明钢管混凝土墩柱具有优异的抗爆炸性能。Qasrawi 等[13]进一步基于数值仿真验证了FRP 包裹对钢管混凝土柱抗爆性能具有改善作用。Li 等[14]基于接触爆炸试验和数值模拟，分析了复式钢管混凝土墩柱在接触爆炸作用下的局部损伤破坏情况及其抗爆性能。

图1 爆炸荷载作用下倒塌的桥梁[2-3]Fig.1 Collapse of bridges under blast loading[2-3]

对于桥梁墩柱上爆炸荷载的分布规律研究方面，Williamson 等[3]指出在地面爆炸时，远距离爆炸条件下作用在桥墩上的爆炸荷载可以近似成均布荷载，而近距离爆炸条件下桥墩上的爆炸荷载可以近似为三角形荷载。Williams 等[15]基于墩柱抗爆试验和数值模拟，得到了在地面爆炸时，作用在圆形和方形截面墩柱表面的爆炸荷载冲量分布，认为在横截面上其分布仅与爆炸距离和墩柱尺寸有关，并进一步提出了墩柱上的荷载预测方法。Fujikura 等[16]基于Bruneau 等[12]的试验，研究了爆炸作用下桥梁墩柱上的超压峰值和冲量沿墩柱高度的分布，指出了爆炸荷载在圆截面墩柱上存在衰减，但并未展开讨论其影响因素。Qasrawi 等[17]基于数值模拟，通过改变圆截面墩柱的直径和TNT 爆炸的比例距离，提出了爆炸荷载在墩柱横截面上的反射超压峰值的计算公式。

可以看出，已有大部分桥梁墩柱抗爆研究工作主要集中在桥梁墩柱在爆炸荷载作用下的动态响应与破坏研究，而对于桥梁墩柱上爆炸荷载的分布规律研究相对较少，缺乏综合考虑爆心高度、炸药当量、爆炸距离和墩柱直径等因素影响的爆炸荷载沿墩柱高度和横截面方向分布规律的研究。此外，已有的爆炸荷载计算方法通常假定结构反射面无限大[18]，不适用于桥梁墩柱等细长构件。与爆炸荷载在建筑柱上作用分布[18-19]不同，桥梁墩柱常以独立形式存在，爆炸荷载在其表面会发生绕射作用。本文采用显式动力有限元程序LS-DYNA，基于已有钢管混凝土墩柱的野外爆炸试验[20]，通过对比数值模拟和试验量测得到的柱迎爆面和背爆面不同位置的冲击波超压时程曲线，验证数值模型中炸药和空气的有限元模型、材料参数和数值算法的正确性；分析比例距离为0.5～2.1 m/kg1/3、爆心高度为0～0.3 倍墩柱高度以及墩柱直径为0.15～1 m 时，爆炸荷载沿墩柱高度和横截面方向上的分布规律；探讨爆炸荷载作用在桥梁墩柱上总净冲量的简化计算方法。

1 钢管混凝土墩柱爆炸试验[20]

孙珊珊[20]共开展了三炮次(SC-1，SC-2，SC-3)圆形截面钢管混凝土墩柱的TNT 装药爆炸试验。本文选取SC-1 墩柱爆炸试验，如图2 所示。该试验炸药当量W=3 kg，炸药中心距柱前表面距离(爆炸距离)R=1.6 m，比例距离Z=R/W1/3=1.1 m/kg1/3，炸药中心距地面高度(爆心高度)hb=0.9 m。钢管混凝土柱高度Hm=1.8 m，采用外径0.27 m、壁厚7 mm 的Q235 热轧无缝钢管，内浇C40 混凝土。通过在墩柱前表面(测点1#，2#和3#)和后表面(测点4#，5#和6#)柱底、柱中、柱顶以及炸药另一侧相同爆炸距离处(测点7#)布置超压传感器测量爆炸冲击波超压荷载时程(见图2)。

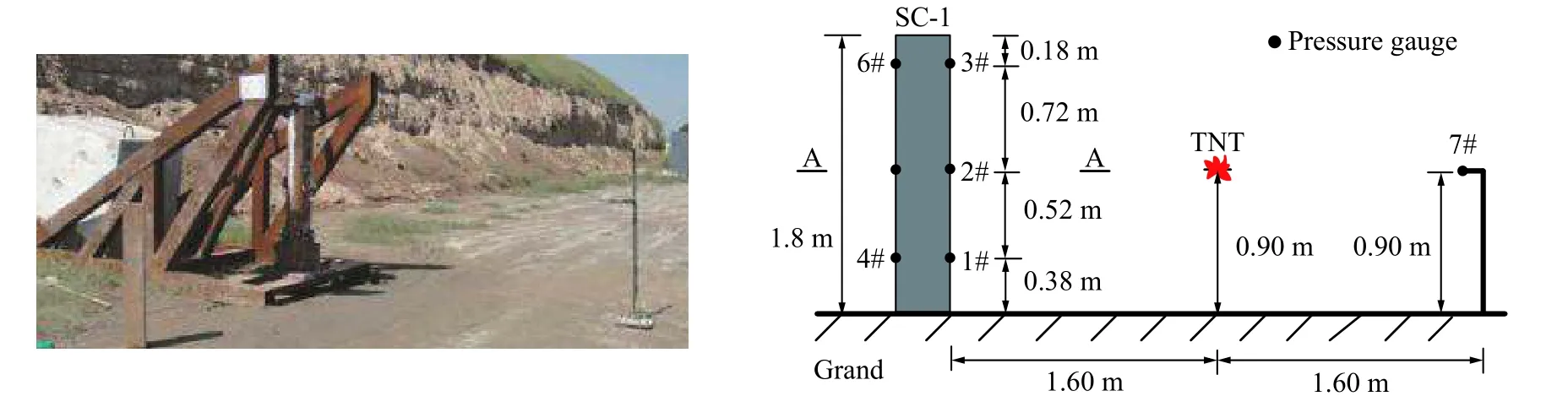
图2 SC-1 墩柱爆炸试验布置[20]Fig.2 SC-1 bridge column blast test setup[20]

2 数值模拟

2.1 有限元模型

SC-1 墩柱爆炸试验有限元模型如图3 所示。该模型由TNT 炸药、空气、钢管混凝土墩柱和刚性地面组成。刚性地面通过关键字*RIGIDWALL_PLANAR 实现，其余部分采用八节点六面体单元建模。钢管混凝土墩柱采用Lagrange 网格描述(*SECTION_SOLID)，炸药与空气采用ALE 网格描述(*SECTION_SOLID_ALE)。炸药与空气设置为共节点连接以便爆炸冲击波能够在空气中传播。采用多物质流固耦合算法(*CONSTRAINED_LAGRANGE_ IN_SOLID)定义ALE 网格与Lagrange 网格(即炸药、空气与柱)之间的相互作用。根据实际工况，将钢管混凝土墩柱边界条件设为底端固定、顶端铰接，将空气边界设为无反射边界(*BOUNDARY_NON_REFLECTING)。基于网格收敛性分析确定炸药与空气网格尺寸为20 mm，圆形钢管混凝土墩柱边缘网格尺寸为23.5 mm。计算模型共759 570 个单元。

图3 有限元模型Fig.3 Finite element model

2.2 材料本构模型

由于本文研究墩柱上爆炸荷载的分布情况，并不关注结构响应，而且试验中墩柱无明显变形。因此在有限元模型中，钢管混凝土墩柱可以采用刚体材料模型(*MAT_RIGID)模拟。刚体材料模型参数见表1，需要指出的是，表中的弹性模量E与泊松比v，并非刚体的实际值，而是为了在数值模拟中的接触分析而设定的一个合理值[21]。

表1 刚体材料模型参数Table 1 Parameters for rigid material model

空气视为无黏性理想气体，采用*MAT_NULL 材料模型模拟，其状态方程采用线性多项式方程(*EOS_LINEAR_POLYNOMIAL)描述[21]：

式中：p为压力，c0～c6为状态方程系数，µ=1/(V−1)，V为相对体积，E0为初始单位体积内能。空气材料的参数取值见表2。

表2 空气材料模型及状态方程参数Table 2 Parameters for air material model and equation of state

TNT 炸药的爆轰过程采用高能炸药燃烧模型(*MAT_HIGH_EXPLOSIVE_BURN)模拟，该模型需要给出TNT 炸药材料的密度ρ、爆轰速度D和爆轰波波阵面压力(C-J 压力)pCJ等参数。状态方程采用Jones-Wilkins-Lee 方程(*EOS_JWL)描述[21]：

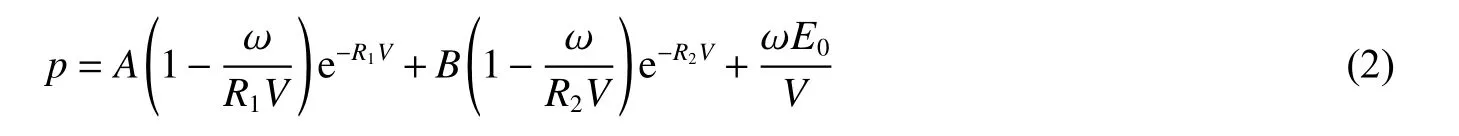
式中：V为相对体积，E0为初始单位体积内能，A、B、R1、R2和ω 为材料常数。本文TNT 炸药材料模型及状态方程的参数取值见表3。

表3 TNT 炸药材料模型及状态方程参数Table 3 Parameters for TNT material model and equation of state

2.3 模型验证

图4 给出了炸药起爆后不同时刻的爆炸冲击波传播的侧视和柱中横截面(A-A 截面)俯视云图，可以看出爆炸冲击波经历了起爆、到达地面、发生地面反射和到达墩柱并发生反射和绕射的典型传播过程。图5 进一步给出了图2 中7 个测点的爆炸冲击波反射超压时程实测曲线和数值模拟结果(采用40 mm 边长的单个单元代替钢管混凝土柱建模即可得到7#的数值模拟结果)。可以看出背爆面的反射超压吻合较好，迎爆面上各测点的超压到达时间比实测结果滞后约0.3 ms，柱底(1#)和柱顶(3#)超压峰值的数值模拟结果相对大2 MPa 左右。由于爆炸试验中对于超压的影响因素有很多，数值模拟中存在一些没有考虑的复杂因素，可能会导致出现上述偏差。例如，文献[20]指出本试验中柱顶位置设置有反力架和抱箍等其他构件对柱顶的爆炸超压存在影响，在数值模拟中，这些因素均没有充分考虑。此外，在迎爆面上，由于未完全燃烧的炸药颗粒以及其他碎屑飞溅物导致试验中柱中传感器安装板上出现密密麻麻的凹点，数值模拟中也无法模拟该过程，因此导致迎爆面上超压的数值模拟结果与实测结果存在一定偏差。而背爆面上的超压主要是爆炸波绕射产生，不存在爆炸飞溅物等的影响，因此其超压影响因素较少，所以背爆面上的数值模拟结果与实测结果吻合较好。综上所述，可认为本文的数值模型、参数及其算法对于预测墩柱上的压力是有效的。

图4 爆炸冲击波传播云图Fig.4 Blast wave propagation contour

3 荷载分布规律

爆炸荷载冲量是研究爆炸冲击波对目标破坏作用的重要参数之一，其大小直接决定了爆炸冲击波的破坏程度[22]，因此本文将爆炸荷载冲量作为研究爆炸荷载分布规律的特征量。考虑到实际工况中桥梁墩柱较高，可能发生的爆炸袭击主要来自于桥墩底部，因此本节以第1 节墩柱为例，分别选取hb/Hm为0(地面爆炸)、0.1、0.2 和0.3 四种爆炸工况，基于第2 节验证过的数值模拟模型与方法，分析爆炸荷载冲量沿墩柱高度和横截面方向的分布规律。参考Williams 等[10,15]的处理方法并考虑精度要求，数值模型中沿墩柱高度方向每隔20 mm、沿墩柱横截面表面圆周方向每隔0.1 倍直径各布置一个测点，共1 800 个测点，如图6 所示。并根据图6(b)中横截面的测点编号，可以得到墩柱任意高度h处横截面上的平均净冲量Ina(h)表达式[15]：

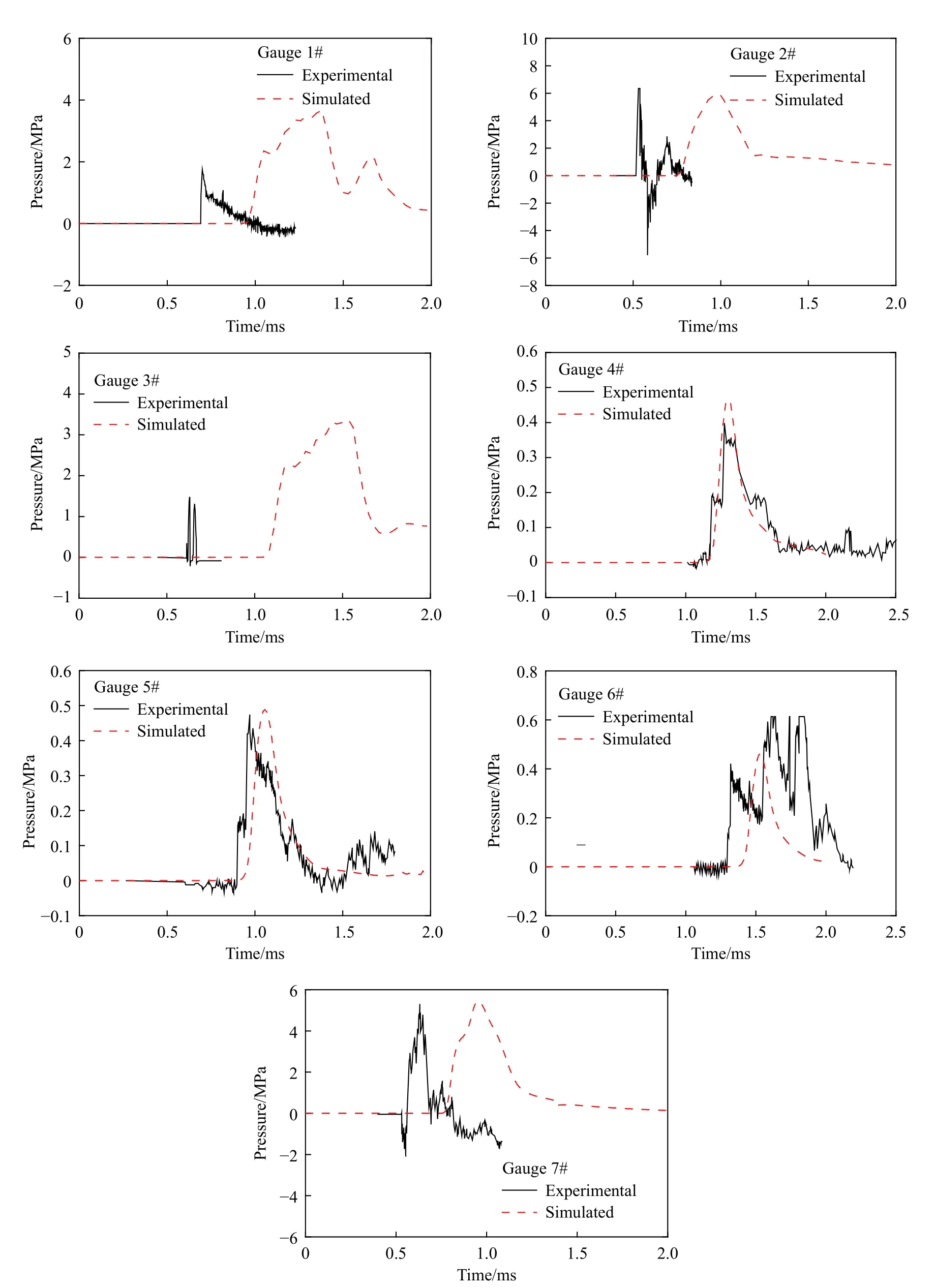
图5 各测点反射超压时程曲线的试验和数值模拟结果对比Fig.5 Comparisons of the experimental and numerical simulated reflected overpressure time-history for each gauge

式中：If(h)为墩柱任意高度h处横截面上测点1 处冲量，称为柱前表面冲量；Ib(h)为该截面测点11 处冲量，称为柱后表面冲量；Ii′ (h)=Ii(h) cosθi，为该截面上各测点冲量沿爆炸冲击波传播方向的分量，Ii(h)为测点i的冲量值，θi为Ii(h)与爆炸冲击波传播方向的夹角，如图6(b)所示。

图6 数值模拟中墩柱表面测点分布[10, 15]Fig.6 Gauging points in numerical simulation[10, 15]

基于第1 节试验，以3 kg TNT 装药、爆炸距离1.6 m(即比例距离为1.1 m/kg1/3)为例，图7 给出了爆心高度分别为hb/Hm为0～0.3 时，柱前表面无量纲冲量If(h)/If(0)(实线)和基于式(3)得到的平均无量纲净冲量Ina(h)/If(0)(点划线)随墩柱无量纲高度h/Hm的变化曲线(左图)。同时，取柱前表面无量纲冲量If(h)/If(0)达到最大值的横截面，给出了该截面爆炸冲量Ii(h)的分布情况(右图)。

图7 不同爆心高度时爆炸荷载冲量沿墩柱高度和横截面方向的分布(Z=1.1 m/kg1/3)Fig.7 Blast loading impulse distributions along column height and cross-section directions for different heights of burst (Z=1.1 m/kg1/3)

3.1 沿墩柱高度方向分布

图7 所示的爆炸冲量沿墩柱高度方向的分布规律并非完全的线性分布，但出于工程应用的简化考虑，本文采用了线性近似，简化了爆炸冲量沿墩柱高度方向的分布特征。从图7 可以看出，当hb/Hm为0 和0.1 时，柱前表面冲量If(h)沿墩柱高度方向从柱前表面底部冲量If(0)线性减小至柱前表面顶部冲量，记为If(Hm)，可认为其满足“单线性”模型，如图8(a)所示。相应的，当hb/Hm为0.2 和0.3 时，If(h)沿墩柱高度方向先从柱前表面底部冲量If(0) 近似线性增大到最大值If(hm)，然后近似线性减小至柱前表面顶部冲量If(Hm)，可认为其满足“双线性”模型，如图8(b)所示。图8(a)“单线性”模型中荷载最不利位置出现在柱底，因此在按该模型进行墩柱抗爆设计时，需对墩柱底部进行加固处理。图8(b)“双线性”模型中荷载最不利位置出现在距地面高度hm处，因此需要对墩柱高度hm处进行加固处理。

图8 柱前表面冲量分布的简化模型Fig.8 Simplified models for blast loading impulse distributions on the column front surface

上述荷载分布模型需要先确定hm、If(0)、If(hm)及If(Hm)值。其中If(0)可根据式(4)得到[23-24]，其余参数通过不同比例距离的数值模拟结果拟合得到，下文逐一进行讨论。

(1)hb/Hm=0

图9(a)给出了不同比例距离(0.5～2.1 m/kg1/3)下无量纲冲量If(h)/If(0)沿无量纲高度h/Hm的分布。图9(b)给出了相应的无量纲冲量If(Hm)/If(0)与比例距离Z的关系，通过拟合得到：

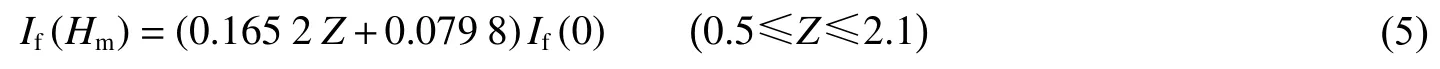
进一步基于“单线性”模型，得到在地面爆炸时，任意柱高位置If(h)的表达式：

图9 不同比例距离下的柱前表面冲量(hb/Hm=0)Fig.9 Blast loading impulses on the column front surface for different scaled distances (hb/Hm=0)

(2)hb/Hm=0.1

图10(a)给出了不同比例距离下If(h)/If(0)沿h/Hm的分布。同样基于拟合图10(b)中If(Hm)/If(0)与Z的关系，并基于“单线性”模型，得到：

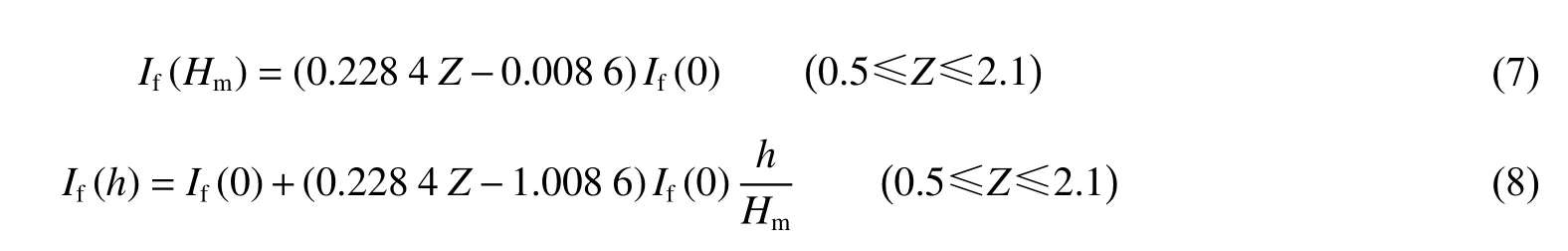
图10 不同比例距离下的柱前表面冲量(hb/Hm=0.1)Fig.10 Blast loading impulses on the column front surface for different scaled distances (hb/Hm=0.1)

(3)hb/Hm=0.2

图11(a)给出了不同比例距离下的If(h)/If(0)沿h/Hm的分布。图11(b)进一步给出了无量纲hm/Hm、If(hm)/If(0)和If(Hm)/If(0)与Z的关系，通过拟合得到：

进一步基于“双线性”模型，得到If(h)的表达式：

图11 不同比例距离下的柱前表面冲量(hb/Hm=0.2)Fig.11 Blast loading impulses on the column front surface for different scaled distances (hb/Hm=0.2)

(4)hb/Hm=0.3

图12(a)给出了不同比例距离下If(h)/If(0)沿h/Hm的分布。图12(b)给出了hm/Hm、If(hm)/If(0)和If(Hm)/If(0)与Z的关系，通过拟合得到：

进一步基于“双线性”模型，得到If(h)的表达式：

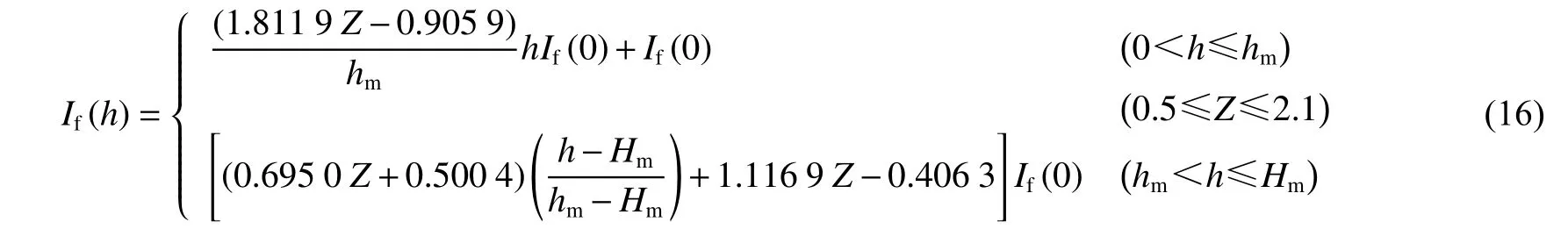
图12 不同比例距离下的柱前表面冲量(hb/Hm=0.3)Fig.12 Blast loading impulses on the column front surface for different scaled distances (hb/Hm=0.3)

上述分析在Williams 等[15]的基础上，进一步讨论了非地面爆炸时，爆炸荷载沿墩柱高度方向的分布规律。但需要指出的是，上述结论的适用范围为0.5 m/kg1/3≤Z≤2.1 m/kg1/3，若比例距离超过此范围，其分布规律可能发生改变。如图10(a)、图11(a)和图12(a)所示，当比例距离接近这一范围的边界时(即比例距离为0.5 或2.1 m/kg1/3)，冲量分布规律的特征开始变得难以近似为线性分布。这一现象说明，除爆心高度外，比例距离也对If(h)沿墩柱高度的分布规律有所影响。同时，从图11(b)可以看出，hm/Hm随Z的增大而增大，说明比例距离越大时，地面反射对爆炸冲击波在墩柱上分布的影响程度愈发显著。

以小汽车后备箱装药为例分析桥梁墩柱的抗爆加固设计。后备箱的一般离地高度约为600 mm，取0.1 倍墩柱高作为“单线性”和“双线性”模型的分界爆心高度，当桥梁墩柱高度大于6 m 时，需按照“单线性”模型分析结果对墩柱底部进行加固，根据本文中hb/Hm为0 和0.1 时的If(h)/If(0)数值模拟结果，发现If(h)/If(0)在0.3 倍墩柱高度以上时已经衰减至80%以下，因此可大致选择对0.3 倍墩柱高度以下的范围进行加固；当桥梁墩柱高度小于6 m 时，可能需要按照“双线性”模型的分析结果对墩柱离地面一定高度处位置进行加固，该高度等于hm，对于不同工况，本文采用不同的hm计算公式，同样根据hb/Hm为0.2 和0.3 时If(h)/If(0)数值模拟结果对于3～6 m 高度的桥梁墩柱，考虑0.5～1.5 m/kg−1/3的比例距离，hm在0～1.7 m 范围内。

3.2 沿墩柱横截面方向分布

图7 给出了爆炸冲量在柱前表面冲量最大值If(hm)所在横截面上的分布。可以看出，墩柱迎爆面上冲量在柱前表面处最大，沿两侧逐渐减小；背爆面上冲量总体很小，各处冲量大小基本相同。同时，在任意高度h截面处，平均净冲量Ina(h)与前表面冲量If(h)存在固定的比例关系，可表示为：

式中：α 为绕射衰减系数，反映了爆炸冲量在绕射过程中的衰减情况，α 越大表明爆炸冲量沿墩柱横截面衰减得越多。α 可能与爆心高度、比例距离和墩柱直径有关，下面进行讨论。

综合考虑比例距离Z和墩柱直径D对α 的影响，图13 给出了地面爆炸时不同墩柱直径(0.15 m≤D≤1 m)和比例距离(0.5 m/kg1/3≤Z≤2.1 m/kg1/3)下的α。由图13 可以看出：(1) 当墩柱直径一定时，α 随比例距离Z的增大而减小，说明比例距离越大时，作用在柱上的爆炸冲量沿墩柱横截面衰减得越少；(2) 当比例距离一定时，α 随墩柱尺寸增大而增大。关于上述结论可做如下解释：比例距离越大说明爆炸作用越弱，爆炸波的传播速度相对较慢，因此衰减效果相对较弱；而当比例距离一定时，墩柱尺寸越大，爆炸波在墩柱表面上传播的距离就越远，意味着爆炸冲量在墩柱横截面上的衰减越多。通过线性拟合，得到α 的表达式：

图13 α 随Z 和D 的变化曲线Fig.13 Variation of α with Z and D

需要指出的是，与Williams 等[15]以及Fujikura 等[16]的研究相比，式(18)表明爆炸荷载沿墩柱横截面方向的分布同时依赖于墩柱直径和比例距离；此外，α 为无量纲量，故该式只需按国际单位制将Z与D的数值代入计算，其适用范围为0.5 m/kg1/3≤Z≤2.1 m/kg1/3和0.15 m≤D≤1 m。

4 总净冲量计算

在桥梁墩柱设计过程中，往往将墩柱简化成一维杆件进行分析，并仅关注作用在其上的总净荷载。基于前文分析得到的爆炸冲击波荷载冲量在圆截面桥梁墩柱上的分布规律，将作用在墩柱上的爆炸荷载冲量转化为作用在一维杆件上的总净冲量In(h)。计算流程为：在讨论范围内(0≤hb/Hm≤0.3，0.5 m/kg1/3≤Z≤2.1 m/kg1/3及0.15 m≤D≤1 m)，由式(4)计算出柱前表面底部冲量If(0)并根据炸药爆心高度在3.1 节中选择对应的公式计算出墩柱任意高度处的柱前表面冲量If(h)，如图14(a)所示；然后，根据比例距离Z和墩柱直径D由式(18)得到绕射衰减系数α，再根据式(17)和已经求得的If(h)计算墩柱任意高度横截面处的平均净冲量Ina(h)，如图14(b)所示；最后，根据In(h)=DIna(h)计算出墩柱任意高度处的总净冲量In(h)，用于桥梁墩柱的抗爆设计，如图14(c)所示。

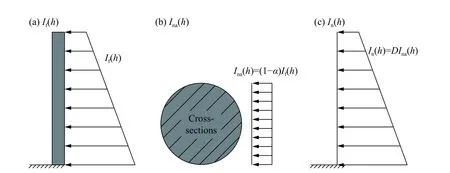
图14 净冲量的一般计算流程Fig.14 General calculation process of the net impulse

5 结 论

本文首先基于LS-DYNA 程序对钢管混凝土墩柱爆炸试验中墩柱迎爆面和背爆面不同位置的冲击波超压开展数值模拟，并与试验量测结果进行了对比，验证了数值模型、参数及其算法的正确性。然后，综合考虑了爆心高度、炸药当量、爆炸距离和墩柱直径等因素，对圆截面桥梁墩柱在承受较低爆心高度爆炸时墩柱上爆炸荷载冲量的分布规律进行了分析，主要结论有：（1）沿墩柱高度方向，柱前表面冲量在地面爆炸以及爆心高度距地面0.1 倍柱高时，可近似为“单线性”分布，在爆心高度距地面0.2 倍柱高或0.3 倍柱高时可近似为“双线性”分布；进一步提出爆心高度低于0.3 倍墩柱高度条件下墩柱前表面冲量的计算公式；（2）沿墩柱横截面方向，爆炸冲击波在墩柱横截面上的绕射衰减随比例距离减小而增大，随墩柱直径增大而增大；进一步给出了圆截面桥梁墩柱任意高度横截面的平均净冲量与柱前表面冲量的关系表达式；（3）提出了TNT 爆炸比例距离为0.5～2.1 m/kg1/3，圆截面桥梁墩柱直径为0.15～1 m，爆心高度低于0.3 倍墩柱高度条件下，墩柱所受到的总净冲量的简化计算方法。