超大直径泥水盾构软土地层推力、转矩分析与计算

王 凯, 孙振川， 牛紫龙， 王国安， 李凤远， 张 兵

(1. 盾构及掘进技术国家重点实验室， 河南 郑州 450001； 2. 中铁隧道局集团有限公司， 广东 广州 511458； 3. 汕头市苏埃通道建设投资发展有限公司, 广东 汕头 515000)

0 引言

伴随城市化进程推进，我国成为地下空间开发利用需求与规模最大的国家，“十二五”期间我国城市地下空间建设量年均增速20%以上[1]。隧道掘进机被广泛应用在地下工程中，目前全国设备保有量近3 000台，具有代表性的泥水盾构正向高水压、大直径、智能化方向发展[2-3]。大直径盾构断面内涉及多种地层，对转矩、推力确定以经验为主，缺乏有效的计算模型。在Krause模型中，总推力F=βD2，总转矩T=αD3(D为盾构或开挖面直径)，其中系数α、β依经验确定，可操作性较差。U.Ates等[4]以262台盾构/TBM推力、转矩数据为样本，拟合不同类型掘进机的推力、转矩与直径、刀具数量等的规律，用于界定载荷范围。盾构推力及转矩由设备、地层、掘进参数多因素共同决定，比TBM更复杂，仅依靠已有统计经验、数据已无法适应盾构发展的需要。相关文献对土压盾构载荷研究较多，并取得了丰富的成果。管会生等[5]对刀盘转矩进行全面分析，推导了转矩分量的计算公式; 施虎等[6]提出土压盾构掘进中总阻力分项组成及各项阻力计算公式，为土压盾构单一地层下掘进提供了载荷预测模型； 徐前卫等[7]以土压平衡盾构为例，研究刀盘转矩的理论计算方法及其与其他参数之间的相互关系并开展了模型试验，对理论研究成果加以验证； 吴起星等[8]在软硬岩交互条件下对刀盘的载荷变化规律进行了研究； ZHOU Xiaoping等[9]在考虑复合式土压盾构刀具配置特点前提下，研究了土岩互层条件下刀盘转矩的计算模型。相比土压盾构，相关文献对泥水盾构推力、转矩计算模型研究偏少。张志奇等[10]统计了不同地质分段的盾构掘进参数，开展针对盾构掘进速率与刀盘转矩的多元回归分析，得到适用于复杂地层的掘进参数回归模型； 杨志勇等[11]以常规刀盘泥水平衡盾构为例，推导出刀盘转矩计算公式，可对单一地层条件下盾构转矩进行预测。泥水盾构在泥浆支护下工作，刀盘与泥浆之间的摩擦阻力矩受尺寸效应影响不可忽略，但理论计算困难；超大直径盾构掌子面一般涉及多种地层且力学性质差异大，不适宜将地层简化为单一地层。为解决上述问题，本文结合某泥水平衡盾构特点，分析超大直径泥水盾构在软土地层下推力、转矩组成项； 利用盾构空转转矩反算流体阻力矩，提出在多层软土地层下泥水盾构推力、转矩的计算模型； 利用地层力学参数对模型进行仿真验证，分析影响盾构推力、转矩的主要因素。利用该模型对软土地层盾构推力、转矩开展预测，可指导掘进参数选取及对应预警阈值设定。

1 盾构特点及总推力、转矩的组成

为加快区域经济发展，沿海某地规划了海湾通道工程，该通道全长6.68 km，其中盾构段长3.05 km，依线路特点可划分为全断面软土段、含孤石的软土段及基岩突起段，其中3段海域基岩突起段侵入隧道范围，极大地增加了工程难度。隧道底部位于平均潮水位以下23.0～36.0 m，最大水压近0.4 MPa。工程采用超大直径泥水盾构施工(主机结构见图1)，盾构采用常压刀盘及伸缩摆动式主驱动设计。常压刀盘上配置滚刀及软土类切削刀具，主驱动通过摆动以扩挖。伸缩借助主驱动后部设计的主驱动油缸牵拉作用，用主驱动油缸压力可推算出主驱动处的推力。基于在泥浆支护下掌子面保持稳定的前提下，盾构总推力F主要由刀具切削阻力F1、刀盘泥水阻力F2、刀盘侧面与地层摩阻力F3、盾体泥水阻力F4、盾壳摩阻力F5、盾尾与管片摩阻力F6及后配套摩阻力F7组成；盾构转矩T由切削转矩T1、刀盘侧面与土层阻力矩T2、轴承摩擦阻力矩T3、主轴密封阻力矩T4、刀盘在流体中摩擦阻力矩T5组成。

F=F1+F2+F3+F4+F5+F6+F7。

(1)

T=T1+T2+T3+T4+T5。

(2)

图1 泥水盾构主机结构图

2 盾构推力、转矩分项载荷的计算

2.1 刀具与土体作用载荷

刀盘配置的滚刀刀高为225 mm，切刀布置高度为185 mm，刀高差为40 mm。处于软土地层时，滚刀挤压土体，切刀切削土体。投影面示意图如图2所示。滚刀与土体接触区域向掌子面投影面积为So、向垂直掌子面方向投影面积为Sh，滚刀与软土作用垂向力为F11，滚刀与软土挤压过程中的阻力矩为T11。

(3)

(4)

式(3)—(4)中：So、Sh与滚刀结构及刀高差相关；σxi为滚刀i所处位置侧向土压力；ri为滚刀i到刀盘中心距离；n为滚刀数目。

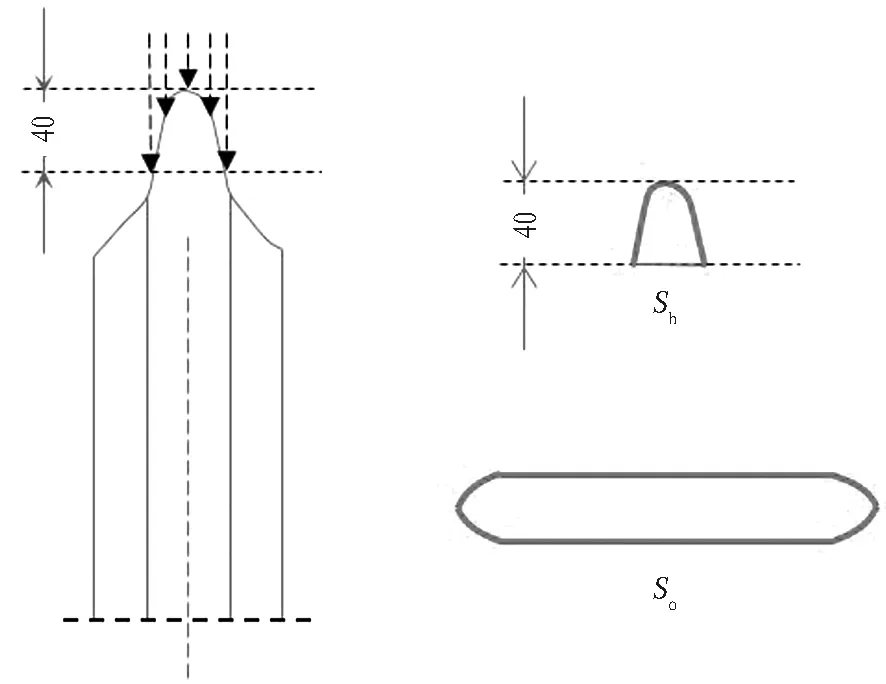
图2 投影面示意图 (单位： mm)

切刀切削载荷计算中切深是关键参数之一，其不但与贯入度Pr有关，还与切刀布置方式有关(示意见图3)。考虑切刀轨迹重合性，提出切深计算方法，将切刀划分为k个切削单元[12]，wj、βwj为第j组的切削宽度和对应角度，子切削单元切深

(5)

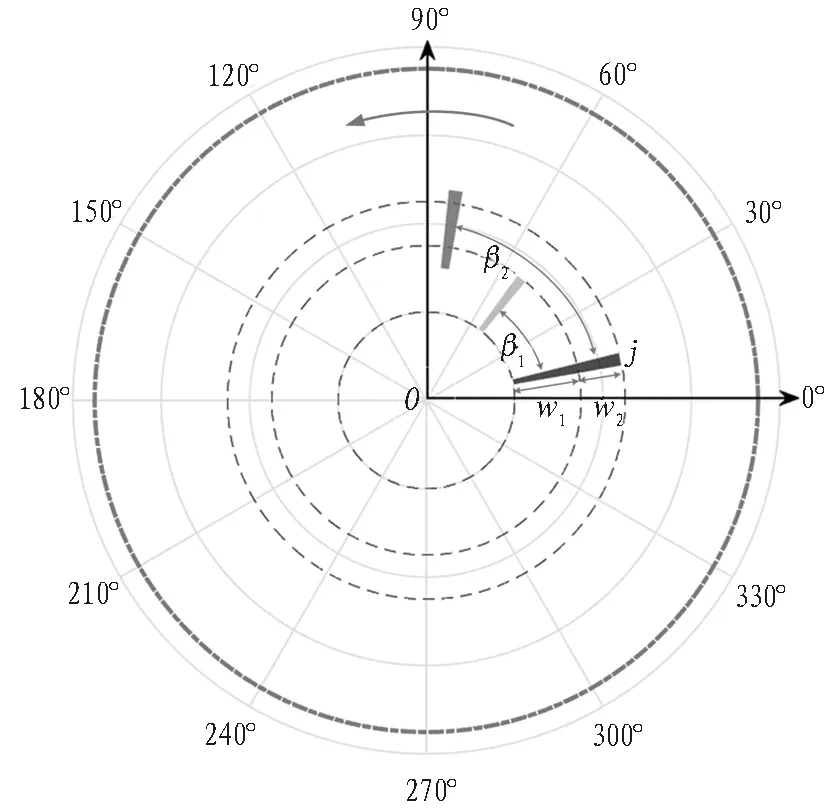
图3 切刀轨迹分布图(以某切刀单元数是2为例)

Fig. 3 Cutter path distribution on cutterhead (with unit cutter of 2)

切削单元j平行于掌子面方向受力Fvj、垂直掌子面方向受力Fhj计算如下[13]：

Fvj=(γhN1+cN2)[L1(1+tanφ1tanη1)+L2(1+tanφ1tanη2)]b-pcos(δ+φ1)-cabh。

(6)

Fhj=(γhN1+cN2)[L1(tanφ1-tanη1)+L2·(tanφ1-tanη2)]b+psin(δ+φ1)+cabhcotδ。

(7)

式(6)—(7)中：N1=eπtan φ2+tan2(45°+φ2/2)；N2=(N1-1)cotφ2；γ为土体重度；h为切深；L1、L2、η1、η2为刀具几何参数；φ1为土体与切刀内摩擦角；φ2为土体内摩擦角；δ为切削土体与水平面的夹角；b为切刀宽度；c为土体黏聚力；ca为土体与切刀黏聚力；p为切刀对切削土体的作用力。

通过对切削单元Fvj、Fhj求和，分别得到单把切刀平行方向受力Fv、垂直方向受力Fh，进而求得切刀与软土作用垂向力F12与软土切削力矩T12。

F1=F11+F12。

(8)

T1=T11+T12。

(9)

2.2 泥水对刀盘的挤压力

受净挤压面积Sthrust和面板中心泥水压力pslurry影响，泥水对刀盘面板的挤压力

F2=pslurry·Sthrust=pslurry·πRb2。

(10)

式中Rb为主轴承外圈半径，取3.8 m。

2.3 刀盘与地层侧面载荷

刀盘与掌子面地层几何关系如图4所示(假设分3种地层)。p11为刀盘圆周位置垂直土压力，p12为刀盘圆周位置侧向土压力，μc为刀盘侧面与泥皮之间摩擦因数，Lc1为刀盘侧面与土体接触部分长度，取0.5 m。某点x(对应角度θ)受到土体对其垂向接触压力

pθ=p11sinθ+p12cosθ。

(11)

图4 刀盘与开挖地层几何关系图

Fig. 4 Geometrical relationship between cutterhead and strata

盾构掘进时，刀盘由平动和转动2个分运动组成，图5所示点x速度v由转动线速度v1和掘进速度v2合成，摩阻力f与v方向相反，f可分解为转动方向阻力f1和掘进方向阻力f2，进而计算刀盘侧面在掘进方向摩擦阻力和转动摩擦阻力矩。

(12)

(13)

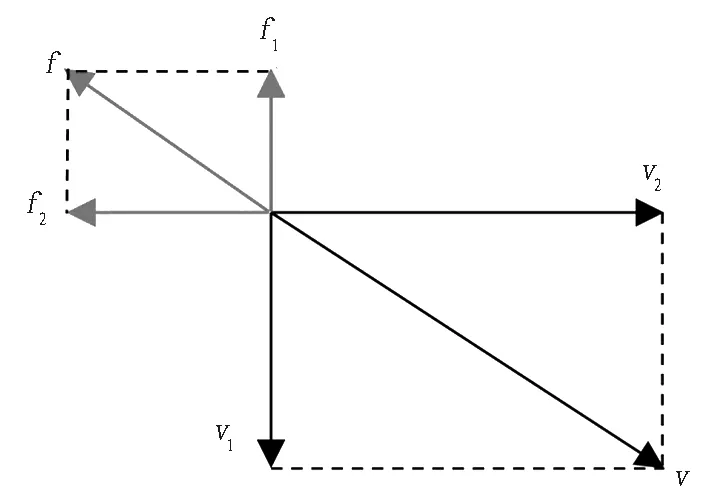
图5 摩阻力分解图

(14)

同理，刀盘侧面的摩擦阻力矩

(15)

2.4 轴承摩擦及密封阻力矩

盾构使用三滚子轴承可承受轴向、径向及转矩载荷，轴承摩擦阻力矩T3分2部分，即推力作用在轴向轴承上产生的阻力矩T31和刀盘作用在径向轴承上产生的阻力矩T32[14]。

T31=(F1+F2+F3)·μb·Rt。

(16)

T32=Wch·μb·Rr。

(17)

Wch=Wcg-γ泥水Vc。

(18)

式(16)—(18)中：μb为滚动摩擦因数，取0.004；Rt为推力滚子轴承接触处到盾构中心轴线距离，取3.658 m；Wch为泥水中刀盘的浮重；Wc为刀盘质量，取5.40×105kg；Vc为排水量，取340 m3；Rr为径向滚子轴承接触处到盾构中心轴线距离，取3.494 m。

为将泥水、渣土等隔离在主轴承外，主轴承设计多道密封进行防护。因刀盘旋转运动密封圈与金属表面间摩擦产生阻力矩T4，主轴承密封摩擦阻力矩与轴承结构、密封压力有关。

T4=2πRs2psnsμs。

(19)

式中：Rs为密封圈安装半径；ps为密封线压力，取1.0 kN/m；ns为密封圈数目；μs为金属与密封圈之间的摩擦因数，取0.2。

主轴承外密封4道，半径为3.60 m； 内密闭3道，半径为2.72 m。

2.5 刀盘在流体中摩擦阻力矩

刀盘旋转时刀盘与泥水的剪切作用产生剪切阻力矩T5。膨润土泥浆可通过Herschel-Bulkley描述来拟合[15]：

(20)

对于配比为50 kg/m3的膨润土、质量分数为2%CMC(相对膨润土)的泥浆，τ0=5.41 Pa,k=0.21,n=0.69。刀盘与泥浆接触面面积为S2，取微元dS2； 微元与回转中心距离为re；δe为微元至边界的距离；则流体阻力矩

(21)

T5=Ae+Beω1.69。

(22)

式(21)—(22)中：ω为旋转速度；Ae、Be为与刀盘结构相关的待定常数，可结合盾构空转时转矩参数来进行确定。

2.6 盾体泥水阻力

D为盾构直径，pslurry为泥水压力，泥水对盾体的挤压力

(23)

2.7 盾壳摩擦阻力

盾体与地层之间摩擦因数μ1=0.1，D=15.01 m，盾体长度L盾体=15 m，p11为垂向土压力，p12为侧向土压力，可通过积分计算盾壳与土层之间的摩阻力

(24)

2.8 盾尾与管片摩擦阻力、后配套阻力

盾尾与管片摩擦阻力

F6=μ2(Wsn4+πD1bTpTn5) 。

(25)

式中：μ2为盾尾与管片摩擦因数，取0.15；Ws为管片所受重力，取1 360 kN；n4为管片环数，取2；D1为管片外径，取14.5 m；bT为每道盾尾刷与管片接触长度，取0.3 m；pT为盾尾刷密封压强，取0.07 MPa；n5为盾尾密封道数，取5。

后配套摩擦阻力F7,主要由后配套设备所受重力Fback和后配套轮对与轨道之间摩擦阻力μback决定,后配套所受重力取19 600 kN,μback取0.15，则

F7=μback·Fback。

(26)

3 模型验证及影响因素分析

取全断面软土段进行验证。672环刀盘与地层位置图如图6所示。刀盘中心埋深h0=28.60 m，水层hw=2.89 m，刀盘面板内②1淤泥地层h2=6.48 m，②3淤泥混砂h3=1.48 m，③4中粗砂地层h4=7.05 m。地层详细参数如表1所示。

(a) 刀盘与地层位置关系

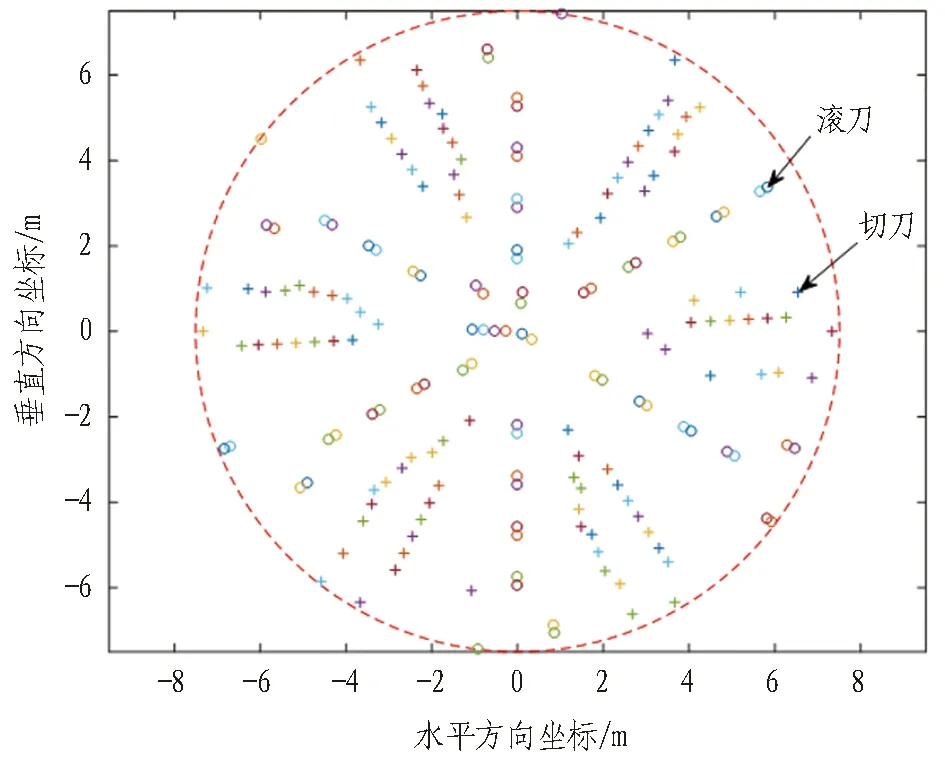
(b) 刀具位置

根据提出的模型，利用MATLAB编制掘进时总推力、转矩计算模型并与672环实际工况数据进行比对，实际掘进中pslurry=0.318 MPa，转速为1.0 r/min，贯入度Pr在28.4 mm/r左右波动。刀盘掘进工况转矩与理论预测转矩的对比如图7所示。可以看出： 实际转矩为2 300～3 200 kN·m(均值2 720.8 kN·m)，理论转矩为2 400～3 050 kN·m(均值2 608.7 kN·m)，实际转矩与理论转矩高度吻合，用均值进行比较，误差为-4.2%。

表1 地层力学性质参数

图7 刀盘实际转矩与理论转矩对比图

Fig. 7 Comparison betwee actual torque and theoretical torque of cutterhead

伸缩摆动式主驱动油缸推力及总推力2个重要指标的理论值和实际值的对比如图8所示。可以看出： 1)伸缩摆动式主驱动油缸实际推力围绕理论推力上下波动，波动的范围为±200 kN(误差控制为±3%)，对伸缩摆动式主驱动油缸推力预测精度很高； 2)对盾构总推力预测最大误差能达到4 000 kN，主要由于盾壳与土体摩擦阻力在总推力中占比很大，影响摩擦阻力的因素较多(比如摩擦因数难以准确取值)，但相对Krause模型或者Ugur Ates的回归模型，在精度上仍有很大优势。

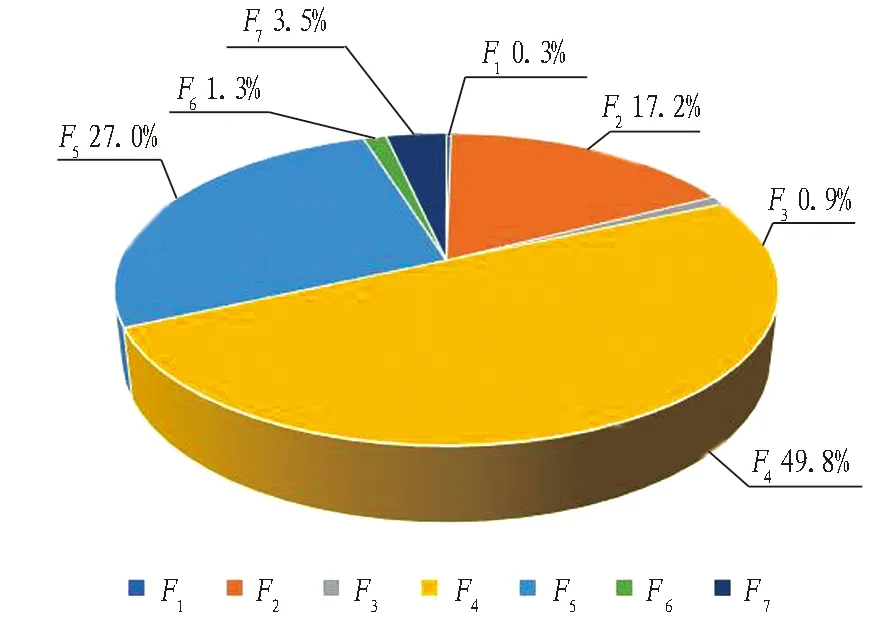
各分项阻力矩在刀盘总转矩中占比如图9所示。可以看出： 1)对转矩贡献量大的T1占比为60.0%，T5占比为26.7%，T3占比为9.6%，T4占比为3.6%； 2)在总推力中，F4占比为49.8%，F5占比为27.0%，F2占比为17.2%，F7占比为3.5%，F6占比为1.3%，其中F2和F4均由泥水压力作用形成，泥水阻力占总推力合计达到67%。由此可见，转矩主要消耗在刀具切削土体中，推力主要用于克服泥水阻力和摩擦阻力。

(a) 伸缩摆动式主驱动油缸推力

(b) 盾构总推力

Fig. 8 Comparison between theoretical thrust force and actual thrust force of shield

Krause模型中，统计数据认为α=9～23，β=500～1 200。以D取15.01 m为例，总推力为1.12×105～2.70×105kN，转矩为3.04×104～7.78×104kN·m。Ugur Ates通过对泥水盾构的推力、转矩进行统计，提出如下的拟合规律：

转矩yT=442.51e0.292 5x(R2=0.88)。

(27)

推力yF=10 269e0.199 7x(R2=0.61)。

(28)

式(27)—(28)中x为盾构直径。

令x=15.01 m，预测的推力为2.06×105kN，转矩为3.60×104kN·m。Krause模型、Ugur Ates回归与现场数据对比差距很大，主要原因是仅通过盾构推力、转矩与开挖直径的关系，忽视埋深、地层力学参数、装备特点等多因素，造成偏差较大，而本模型则克服了上述缺点，在预测精度上显著提升。

(a) 转矩中各分项占比

(b) 推力中各分项占比

4 结论与讨论

本文根据超大直径泥水盾构的特点，分析了泥水盾构推力、转矩的主要组成分项，结合地层特点提出推力、转矩的分项计算模型并编制计算程序，通过与现场掘进数据进行对比验证及分析，得出如下结论。

1)推力、转矩的现场实测值与理论计算值误差在±10%内，两者具有较高的吻合度，证明该模型准确有效。对比Krause模型、Ugur Ates回归，在预测精度上有较大提升，能够依据盾构的结构、地层等参数合理地估算出推力、转矩值，进而为盾构设计、施工提供指导。

2)通过验证段计算分析发现，盾构总转矩的60%用于切削土体，其次是刀盘在泥浆中转动克服流体摩擦阻力矩(约占26.7%)，最后是主轴承摩擦阻力矩、主轴承密封阻力矩。采用泥水盾构施工，盾构总推力中67%需要克服泥水对刀盘、盾体的压力，其次是盾壳与土层的摩擦阻力占比27%，盾构总推力受盾构直径、泥水压力(盾构埋深)影响很大，深埋盾构必须在设计时配备较大的推力，相反切削软土时垂向力对总推力影响可忽略不计，故转矩指标对地层变化更为敏感。

3)刀具的载荷对切削转矩计算至关重要，后续可通过在刀具上设计载荷测量装置，通过数据的聚类、拟合形成切削刀具在不同地层作用时基础数据库，提升计算模型在不同地层的适用性与计算精度。此外，海域基岩段推力、转矩计算相比软土段更加复杂，掌握推力、转矩受基岩起伏高度影响规律对施工指导意义更大，是进一步研究的重点。