基于现场实测的深埋风积沙隧道围岩压力计算方法研究

2020-01-01王志杰王如磊徐君祥李学广窦廷明

隧道建设(中英文) 2019年12期

王志杰, 王如磊, 徐君祥, 吴凡, 李学广, 窦廷明, 李炜, 张飞

(1. 西南交通大学交通隧道工程教育部重点实验室, 四川成都 610031；2. 中铁十八局集团第一工程有限公司，河北涿州 072750 )

0 引言

近年来，随着蒙华铁路的修建，在内蒙至陕西段大量隧道穿越风积沙地层。风积沙地层具有粒径小、黏聚力低、抗剪强度低、透水性强、自稳能力差等特点[1-3]。在该地层中修建隧道时，易发生大量诸如衬砌背后空洞、衬砌开裂、流沙、初期支护大变形、二次衬砌开裂等事故。诸多问题均反映出对作用在隧道结构上的风积沙地层压力认识不清的现状，风积沙围岩压力分布特征还有待更深入研究。

当前，作为学术界研究的重点问题，很多学者对不同地质条件下隧道围岩压力的作用模式与计算方法进行了研究，如黄土隧道[4-5]、软弱围岩隧道[6-7]等。李鹏飞等[8]对国内众多典型隧道围岩压力进行统计分析，研究隧道围岩压力的总体分布特征及其与围岩级别、隧道埋深的关系；房倩等[9]和于丽等[10]研究了高速铁路隧道围岩压力的变化规律和分布特征；卿伟宸等[11]针对多线铁路大跨隧道展开了围岩监测研究。目前，该方面研究极少涉及到风积沙地层，尤其是深埋条件下风积沙围岩压力大小和分布规律尚不明确。本文在前人研究的基础上，依托蒙华铁路王家湾隧道进行现场量测试验，分析初期支护受力特性，依据国内外广泛使用的3种深埋围岩荷载计算方法，得到理论计算值，与实测围岩压力值进行对比分析，得到适用于深埋条件下风积沙地层的围岩压力计算方法和分布特征；并结合数值计算手段，进一步分析在深埋风积沙地层中隧道结构受力特征。研究成果以期为大断面深埋风积沙隧道的支护设计提供参考。

1 工程概况

新建蒙华铁路王家湾隧道位于陕西省延安市安塞县境内，隧道最大埋深约220 m，进口里程DK266+945，出口里程DK274+233，全长7 288 m。隧道地处中朝古地台鄂尔多斯盆地伊陕斜坡区，区内地质构造相对简单。褶皱和断裂不发育，地势东高西低，总体上为倾向西—西北的单斜构造; 隧址区广布白垩系下统砂岩，斜层理极其发育; 区域上无大的构造活动，无大型褶皱和断层。

2 监测方案

为了明确风积沙隧道围岩荷载计算方法及衬砌受力状态，优化初期支护及二次衬砌结构设计，在隧道穿越风积沙Ⅵ级围岩段共布设8个监测断面，每个监测断面设置12个监测点。每个监测点测量包括初期支护及二次衬砌混凝土应变、钢架内力、围岩与初期支护之间接触压力、二次衬砌与初期支护之间接触压力。测点位置、编号如图1所示，压力盒现场安装如图2所示。

3 实测围岩压力分析

为研究深埋风积沙隧道围岩压力分布特征，在DK270+504、DK270+509等8个监测断面测得围岩与初期支护间围岩压力及其分布规律如图3所示。

图1 测点布置示意图

(a) 压力盒

由图3可知，不同断面深埋风积沙隧道围岩压力在全断面上分布形态具有较大的差异性，部分显示隧道上方存在脱空的情况，呈现出非均匀接触压力。究其原因，风积沙隧道属于一种特殊的砂性隧道，其上部围岩存在拱结构，如图4(a)所示。此种情况下，隧道上部荷载为拱内松散砂体压力，围岩荷载呈现如图3(d)所示。而根据测试结果分析，该复合拱结构[12]并不总是存在于隧道正上方，而可能出现隧道偏压的情况，如图4(b)所示，此时作用在隧道结构上的荷载如图3(a)、图3(c)所示。

各断面实测围岩压力的竖直方向分量与水平方向分量的最大值见表1，表中竖直方向分量值是1#—7#测点中分量的最大值，水平方向分量值是2#—11#测点中分量的最大值。

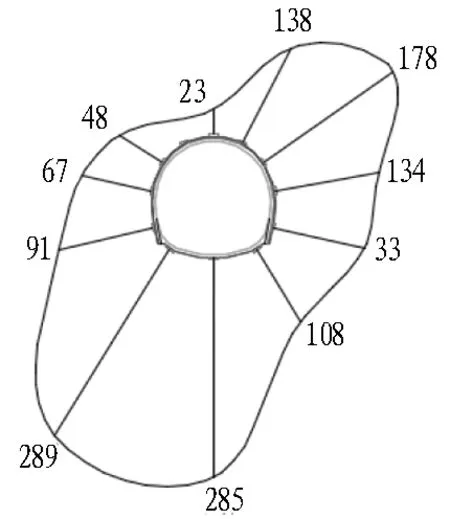
(a) DK270+504断面

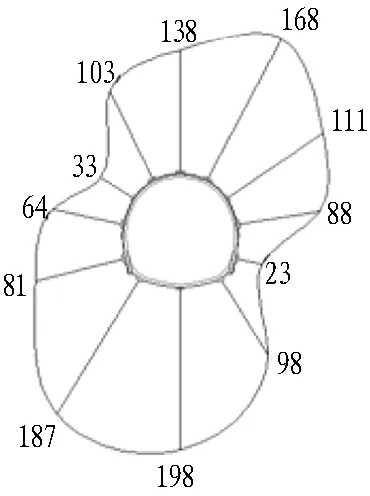
(b) DK270+509断面

(d) DK270+519断面

(e) DK270+524断面

(f) DK270+529断面

(g) DK270+534断面

(h) DK270+539断面

(a) 拱结构在正上方

(b) 拱结构不在正上方

表1实测围岩压力各方向分量最大值

Table 1 Measured maximum value of each direction component of surrounding rock pressure kPa

断面里程围岩压力分量最大值竖直方向分量水平方向分量DK270+504119.51204.35DK270+509145.49132.23DK270+514222.56220.59DK270+51949.36195.87DK270+52456.29170.41DK270+52998.00147.08DK270+534110.85142.13DK270+539129.04187.38

由图3、表1可知，大断面深埋风积沙隧道各断面围岩压力分布较为不均匀，但普遍拱部围岩压力竖直分量较小，拱腰与拱脚围岩压力水平分量较大。

4 深埋风积沙隧道围岩压力计算方法

4.1 计算参数确定

风积沙作为一种典型的砂性土，其黏聚力低、自稳能力差，物理力学特性与黏粒含量及含水率有明显关系。王家湾隧道所穿越风积沙地层夹杂少量黄土，含水量较地表、浅埋风积沙高。隧道风积沙段埋深60 m，洞身净跨度12 m，净高11.6 m。为了明确该种条件下围岩物理力学参数，据此计算隧道承压情况，在现场段取土进行室内物理力学试验，主要包括颗粒密度试验、固结试验，直剪试验等。试验过程如图5所示，所得王家湾隧道风积沙基本物理力学参数见表2。

表2 基本物理力学参数

4.2 围岩压力计算方法确定

目前，国内对于风积沙地层深埋围岩压力荷载计算方法的研究尚不充分，对该条件下计算理论的选择尚未有明确的定论。现以陕西王家湾大断面铁路隧道为例(风积沙段埋深约为60 m，覆跨比H/D=5)，根据已得到的室内物理力学参数，对比普氏理论、太沙基理论和现行TB 10003—2016《铁路隧道设计规范》[13]中深埋隧道围岩压力计算方法这3种主流深埋围岩压力计算方法。

1)普氏理论，公式见(1)—(3)。

q=γha；

(1)

(2)

p=γhatan2(45°-φ0/2)。

(3)

式中:q为竖向压力荷载;γ为地层重度;ha为自然平衡拱高度;bt为自然平衡拱半跨度;b为隧道净宽的1/2;H为隧道洞室高度;φ0为岩体内摩擦角;fm为岩体的坚固系数，fm≈tanφ0=0.35[14];p为水平压力荷载。

2)太沙基理论,公式见(4)—(6)。

q=(γbt-c)/(λtanφ0)(1-e-λntan φ0);

(4)

bt=b+Htan(45°-φ0/2);

(5)

p=qtan2(45°-φ0/2)。

(6)

式中:c为地层内黏聚力;λ为地层侧压力系数，一般取1.0;e为水平荷载计算值;n为相对埋深系数，n=h/bt。

3)TB 10003—2016《铁路隧道设计规范》，公式见(7)—(10)。

q=γh1；

(7)

h1=0.45×2s-1ω;

(8)

ω=1+i(B-5)；

(9)

p=λq。

(10)

式中:h1为围岩计算高度;s为围岩级别;ω为开挖宽度影响系数;B为隧道开挖宽度;i为B每增减1 m时围岩压力的增减率，当B<5，取i=0.2，当B>5，取i=0.1。

基于上述3种理论计算所得的围岩压力各分量与实测最大值对比结果见表3。

表3围岩压力理论值与实测值最大值对比

Table 3 Comparison between maximum theoretical and measured values of surrounding rock pressure

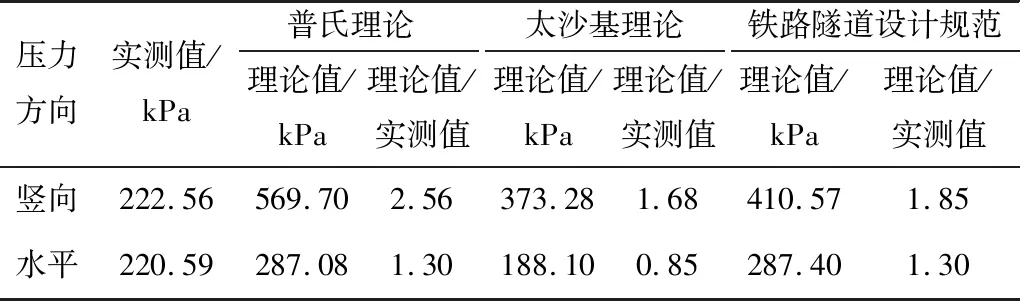
压力方向实测值/kPa普氏理论理论值/kPa理论值/实测值太沙基理论理论值/kPa理论值/实测值铁路隧道设计规范理论值/kPa理论值/实测值竖向222.56569.702.56373.281.68410.571.85水平220.59287.081.30188.100.85287.401.30

由表3可知，在不考虑地下水荷载作用的条件下，TB 10003—2016《铁路隧道设计规范》计算方法和普氏理论在竖直方向和水平方向都偏大；太沙基理论竖直方向理论值也比实测值大，但却是三者中最小的，水平方向理论值比实测最大值稍小，是因为隧道偏压造成一侧水平压力较大，所以相比较而言，太沙基理论计算值与实测最大值是最为接近的。因此，推荐采用太沙基理论计算大断面深埋风积沙隧道的围岩压力。

5 深埋风积沙隧道围岩压力分布规律

确定最大围岩压力计算方法后，还需进一步研究分析隧道围岩压力的分布规律。同时，为了使该分布规律更具有实际意义，需对分布规律进行简化，即需得到深埋风积沙隧道围岩压力的计算图示。

5.1 竖直方向围岩压力计算图式

将实测径向上的围岩压力向竖直方向分解，将各测点竖向分量与拱顶竖向压力进行对比，分析其分布规律。选取DK270+524作为典型断面，各测点围岩压力的竖向分量及其与拱顶竖向荷载的比例均值见表4。

表4DK270+524监测断面围岩压力竖向分量及比例均值

Table 4 Vertical components and proportion mean value of surrounding rock pressure at DK270+524

测点对应位置径向围岩压力/kPa竖向分量/kPa竖向围岩压力均值/kPa比例均值1拱顶43.0043.0043.001.002左30°85.0073.613右30°88.0076.214左60°124.0062.005右60°43.0021.506左80°108.0018.757右80°98.0017.0174.911.7441.750.9717.880.42

注：比例均值为各对称测点均值与拱顶竖向荷载之比。

由表4可知，围岩压力竖向分量最大值并非位于拱顶处，而是出现在隧道左右30°附近。

由于不同断面上各个测点围岩实测压力具有相当大的离散性，因此采用统计法分析其内在规律。将8个监测断面拱顶处压力作为隧道上部荷载计算基准，得到风积沙深埋隧道上部所受围岩竖向荷载及荷载计算比例均值见表5。

表58个监测断面围岩竖向荷载及比例均值统计

Table 5 Statistics of vertical load and proportion mean value of surrounding rock at 8 monitoring cross-sections

监测位置测点荷载均值/kPa比例均值拱顶163.00 1.00左右30°2、369.39 1.10左右60°4、535.19 0.56左右80°6、713.67 0.22

注: 比例均值为各对称测点均值与拱顶竖向荷载之比。

由表5可知，拱顶压力比两侧30°拱腰处压力偏小，但比左右两侧60°和80°处的竖向压力大。偏于安全考虑，建议深埋大断面风积沙隧道竖向围岩压力计算采用如图6所示计算图示，呈“双峰”形分布。荷载呈线性对称分布，拱顶处竖向压力为太沙基理论竖向荷载计算值q，左右30°处峰值推荐取1.0q～1.5q，60°～ 90°处推荐取0.8q。

图6 深埋大断面风积沙隧道竖向围岩压力计算图示

Fig. 6 Vertical surrounding rock pressure calculation sketch of deep large cross-section aeolian sand tunnel

5.2 水平方向围岩压力计算图式

将实测径向上围岩压力按水平方向分解。以断面DK270+524为例，按各测点的实测水平向荷载分量进行对比分析，得到各测点围岩压力分量及比例均值见表6。

表6DK270+524监测断面围岩压力水平分量及比例均值

Table 6 Horizontal components and proportion mean value of surrounding rock pressure at DK270+524

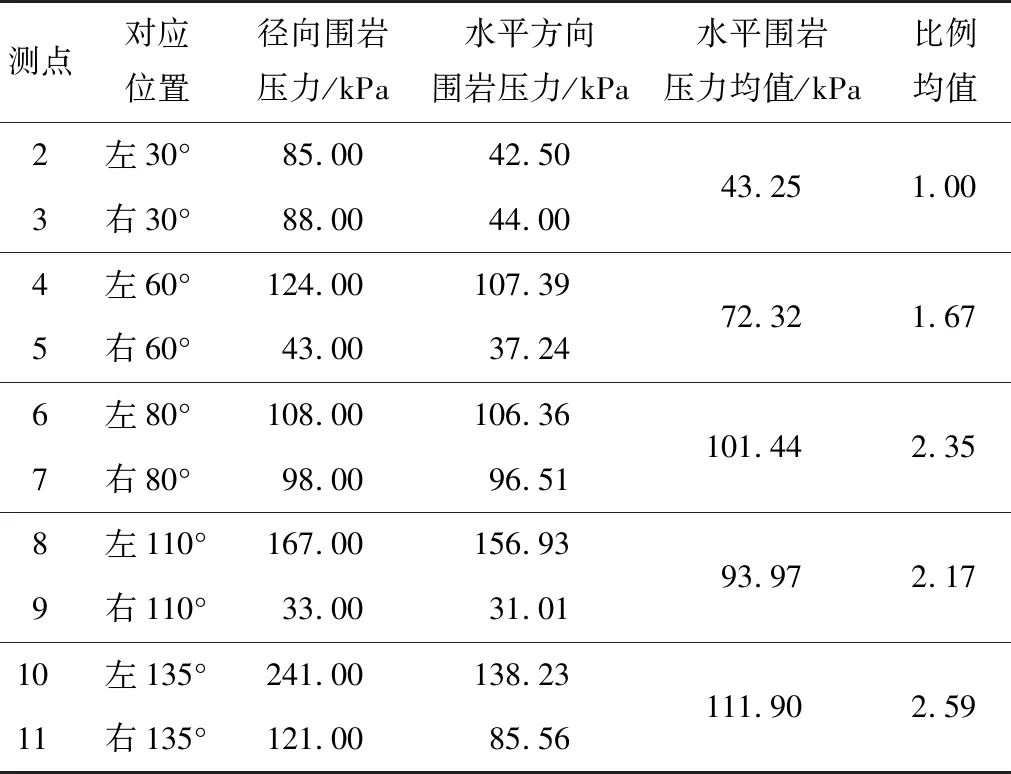
测点对应位置径向围岩压力/kPa水平方向围岩压力/kPa水平围岩压力均值/kPa比例均值2左30°85.0042.503右30°88.0044.004左60°124.00107.395右60°43.0037.246左80°108.00106.367右80°98.0096.518左110°167.00156.939右110°33.0031.0110左135°241.00138.2311右135°121.0085.5643.251.00 72.321.67 101.44 2.35 93.97 2.17 111.90 2.59

注: 比例均值为各对称测点均值与左右30°处荷载均值之比。

对其他监测断面水平分量进行相同计算，统计分析所有断面围岩压力水平分量比例均值见表7。

根据测量数据，得到深埋风积沙隧道围岩水平压力分布如图7虚线所示，呈“阶梯”形分布，与太沙基理论中推荐的侧压力梯形分布具有一定相似性，但在拱脚处水平围岩压力凸出。水平围岩压力最大值出现在拱脚部位，越靠近拱脚，水平压力越大。

表78个监测断面围岩水平荷载及比例均值统计

Table 7 Statistics of horizontal load and proportion mean value of surrounding rock at 8 monitored cross-sections

监测位置测点荷载均值/kPa比例均值左右30°2、342.471.00 左右60°4、566.901.58 左右80°6、783.77 1.97左右110°8、959.55 1.40左右135°10、11 119.77 2.82

注: 比例均值为各对称测点均值与左右30°处荷载均值之比。

偏于安全考虑，推荐深埋风积沙隧道围岩压力水平分量按照图7实线所示进行计算。拱顶处水平围岩压力为太沙基理论水平向荷载计算值e，隧道断面左右60°～110°推荐取值1.5e～2.0e，仰拱部位推荐取值2.5e～3.0e。

图7 深埋大断面风积沙隧道水平围岩压力分布图示

Fig. 7 Distribution sketch of horizontal surrounding rock pressure in deep large cross-section aeolian sand tunnel

6 初期支护受力分析

在得到深埋风积沙隧道围岩压力计算图示后，为验证其合理性，可通过计算现场量测的钢架内力、喷射混凝土内力，并与通过数值模拟得出的理论值对比分析，比较二者之间的大小和变化趋势，以此来验证所给出计算图示的合理性。

6.1 格栅钢架内力

选取监测断面中数据较为完整的4个断面，其格栅钢架内外侧应力分布如图8和图9所示,根据应力分布计算得到的轴力、弯矩见表8。量测数据表明: 各监测断面格栅钢架内外侧都是承受压应力的，拱顶和拱肩处压应力较大，边墙和仰拱中心处压应力较小；各断面格栅钢架应力表现出不对称性，大体分布具有“上大下小”的特点，格栅钢架所承受的轴力和弯矩都较小。

6.2 喷射混凝土内力

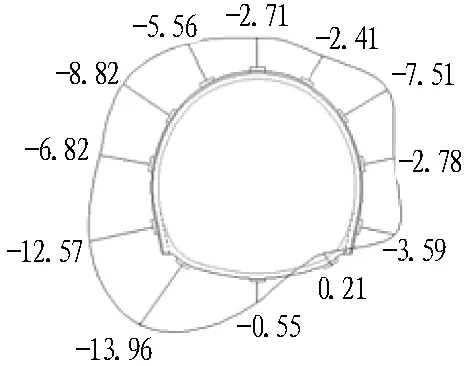
各断面喷射混凝土内外侧应力分布如图10和图11所示，根据应力分布计算得到的轴力、弯矩见表9。量测数据表明: 各量测断面喷射混凝土基本都承受压应力，有少部分区域承受拉应力，但值很小，分布在拱脚处；同样，各断面喷射混凝土内力分布表现出不对称性，喷射混凝土承受轴力较大，弯矩较小。

(a) DK270+504断面

(b) DK270+509断面

(d) DK270+524断面

图8格栅钢架外侧应力分布(单位: MPa)

Fig. 8 Stress distribution on outside of grid steel frame (unit: MPa)

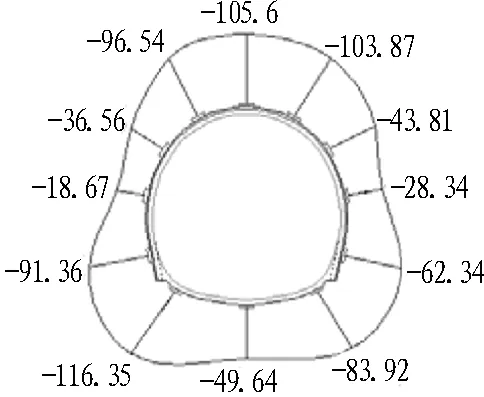
(a) DK270+504断面

(b) DK270+509断面

(d) DK270+524断面

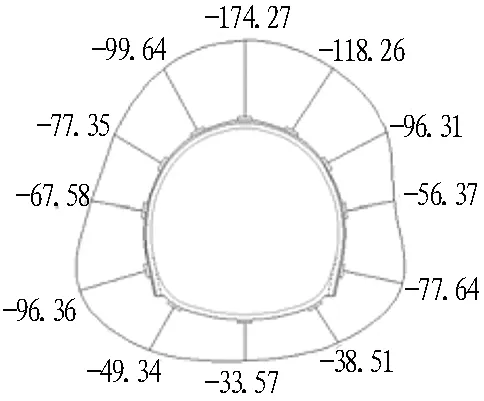
图9格栅钢架内侧应力分布(单位: MPa)

Fig. 9 Stress distribution on inside of grid steel frame (unit: MPa)

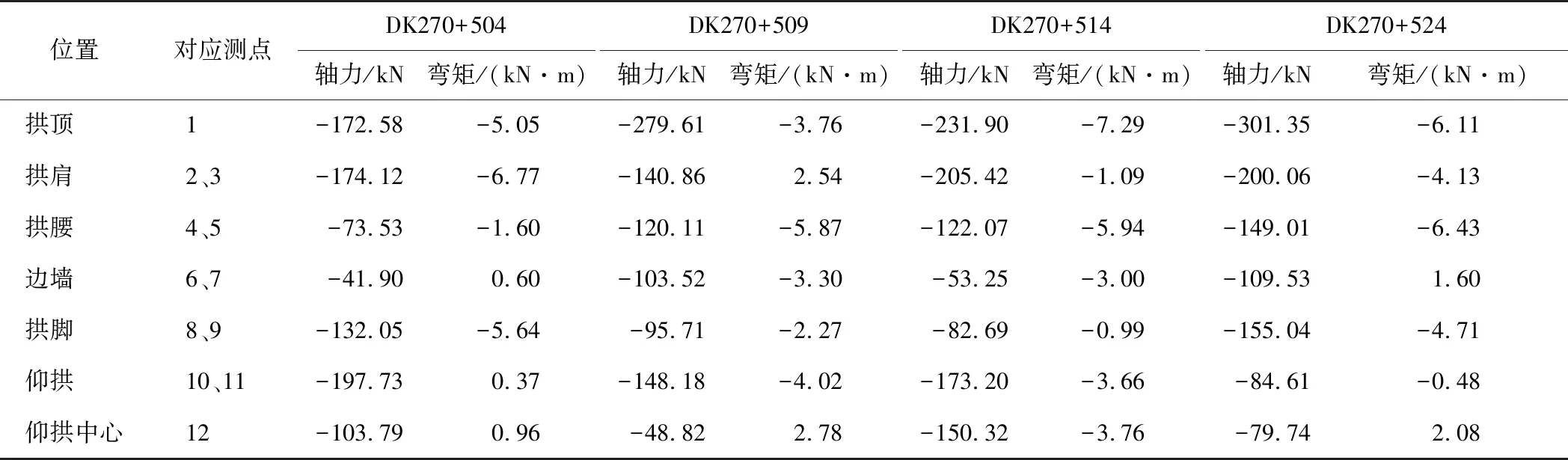
表8 格栅钢架轴力、弯矩汇总表

(a) DK270+504断面

(b) DK270+509断面

(d) DK270+524断面

6.3 实测数据与数值模拟值对比分析

通过对格栅钢架和喷射混凝土内力进行综合计算，得到各量测断面综合轴力、弯矩汇总见表10。

采用大型通用有限元软件ANSYS按照上述荷载计算图示对初期支护受力进行计算分析，竖向荷载q和水平荷载e取值为太沙基理论计算值，见表3；围岩计算参数采用室内试验所得数据，见表2; 初期支护参数见表11，格栅钢架强度折减至喷射混凝土。计算得到初期支护结构轴力、弯矩计算值见表12，轴力、弯矩受力云图如图12所示。

(a) DK270+504断面

(b) DK270+509断面

(d) DK270+524断面

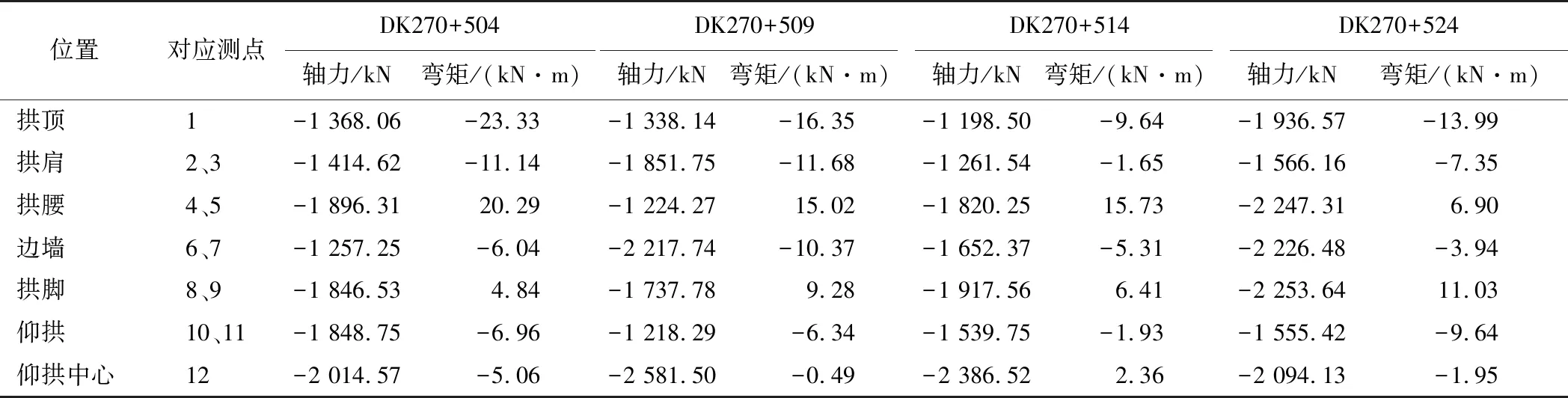
表9 喷射混凝土轴力、弯矩汇总表

表10 综合轴力、弯矩汇总表

表11 初期支护计算参数

表12 ANSYS计算所得内力

对比分析实测数据和依据所给计算图示计算所得内力，计算值最大轴力在仰拱中心，最小轴力在仰拱，最大正弯矩在拱腰，最大负弯矩在拱顶。与实测值虽然稍有出入，但总体上看，两者的轴力、弯矩变化趋势大致是相吻合的，计算值与实测值相比相对较大，具备安全储备空间，由此可以验证所给的计算图示是合理的。

7 二次衬砌结构强度验算分析

进一步对二次衬砌结构强度验算分析，通过数值计算软件对深埋风积沙隧道围岩压力作用模式下的隧道内力进行计算，对比采用太沙基理论计算方法下，隧道二次衬砌结构内力及安全系数的区别。二次衬砌参数见表13。

依据《铁路隧道设计规范》，结合对初期支护围岩接触压力、初期支护和二次衬砌接触压力的现场监测数据，从安全角度考虑，取二次衬砌荷载分担比例为60%。两者荷载结构模型如图13所示。

(a) 轴力(单位: N)

(b) 弯矩(单位: N·m)

表13 二次衬砌计算参数

(a) 深埋风积沙荷载模式

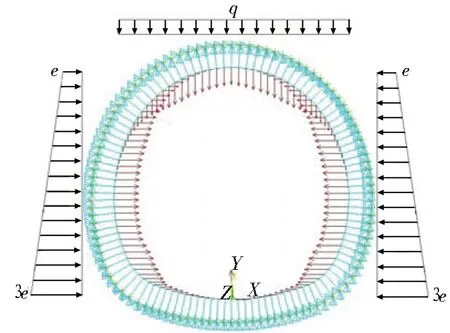
(b) 太沙基荷载模式

对比隧道二次衬砌在推荐深埋风积沙荷载计算模式下和太沙基计算模式下的结构内力，如图14所示。

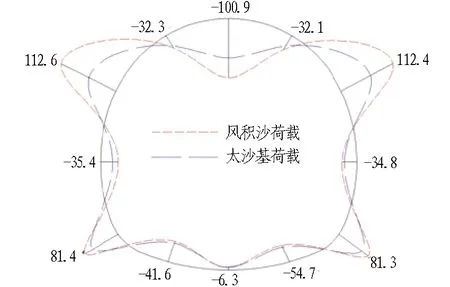
(a) 衬砌弯矩(单位: kN·m)

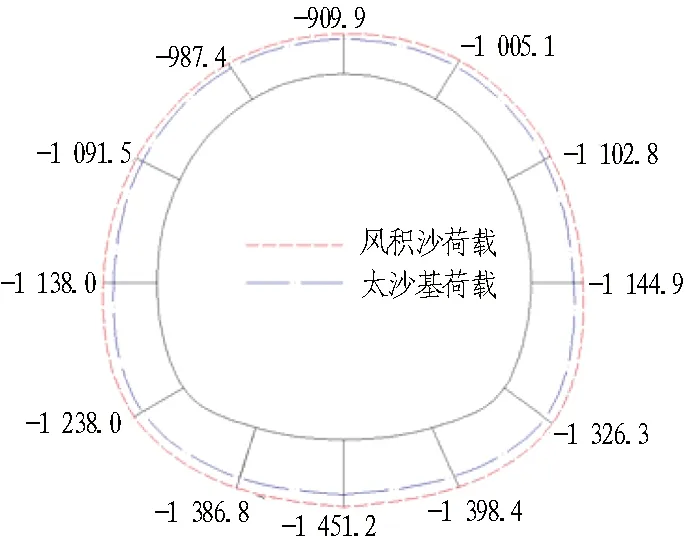
(b) 衬砌轴力(单位: kN)

推荐深埋风积沙隧道荷载计算模式下，二次衬砌所受最大正、负弯矩分别出现在左右拱腰30°处和拱顶处；而在太沙基计算模式下，在拱脚处也出现了最大正弯矩。2种计算方法得到的轴力和剪力分布基本一致。总体上，推荐深埋风积沙荷载计算模式与太沙基计算模式相比，轴力、剪力、弯矩都相对较大。衬砌实际受力状态具有较大的离散性，但通过与计算结果的对比可知，深埋风积沙荷载计算模式下衬砌的受力状态更贴近实际，采用深埋风积沙荷载计算模式是更为合理、安全的选择。

2种计算方法下，隧道二次衬砌安全系数见表14，最小安全系数均出现在拱顶。但相比太沙基理论，根据推荐深埋风积沙荷载计算模式所得安全系数较小，在拱顶和左右拱腰60°处安全系数下降最为明显。

表14不同荷载计算模式安全系数对比

Table 14 Comparison of safety coefficients of different load calculation modes