管道表面特性对流动摩阻系数的影响研究进展

矫 捷，吕宇玲，朱正南，牛振宇

（1.中国石油大学（华东）储运与建筑工程学院/山东省油气储运安全省级重点实验室，山东青岛266580；2.中国石化管道储运公司，江苏 徐州221000；3.西安长庆科技工程有限责任公司，陕西 西安710000）

现阶段集输工艺的发展及油田后期的开发与建设对输油管道的质量要求越来越高。传统的金属管道随着多年的研究及应用，技术已经成熟，但其弊端也日渐暴露。非金属管道因具有使用性能优异、安装及维修成本低的特点，逐渐被广泛应用于原油输送中。非金属输油管道单根管线较长，大大减少了弯头使用量和焊接量，铺设的速度远远高于传统的金属管线。目前对非金属管道摩阻系数的工艺计算还处于探索阶段。因此，需要对非金属管道的摩阻系数进行研究，给工程计算提供指导。基于前人研究，影响非金属管道摩阻系数工艺计算较金属管道不准确的主要因素有两点：非金属管壁内表面粗糙度明显小于金属管道；非金属材质的管道内壁对比金属管道明显更亲油也更疏水。

1 管壁粗糙度对摩阻系数的影响

1933 年，德国著名的水利科学家尼古拉兹基于他两年间所开展的人工粗糙圆管水流阻力实验，即著名的尼古拉兹实验，提出了圆管水流沿程阻力随管内流体雷诺数和管壁粗糙度的变化规律，奠定了水力学中的管流定量分析与计算的经典理论基础[1-7]。G. M. Mala 等[8]通过实验研究了流经不锈钢圆柱形微管和熔融石英的水的流动特性。实验发现，摩阻系数高于传统理论预测的摩阻系数并取决于雷诺数、管壁粗糙度、微管的材料及管径。提出从层流到湍流的早期过渡流态的存在是导致流动阻力较高的原因，并建立了粗糙度-黏度模型来解释微管中的流动特性。

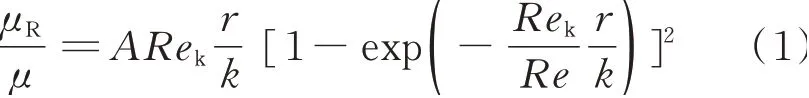
万军伟等[9]采用与尼古拉兹实验一样的对光滑圆管内壁进行人工粗糙化来制成不同相对粗糙度的人工粗糙圆管，但人工粗糙圆管的粗糙化工艺与尼古拉兹不同的是，使用一次涂胶后就可以保证沙粒紧密黏合在有机玻璃圆管内壁的氯仿，所以该实验可以不进行尼古拉兹实验中的二次刷胶工艺，从而避免了在二次刷胶工艺中相对粗糙度比实验设计的粗糙度小，这一改进使实验结果更符合实际的变化规律。在后续研究中[10-12]通过各种不同手段改变固体壁面的粗糙度来探索其对摩阻系数的影响关系，得到的结论是一致的，即摩阻系数会随粗糙度的增大而增大。邹江等[13]从理论出发研究了层流条件下管内壁粗糙度对流动摩阻的影响。研究发现，管内壁粗糙度从粗糙结构疏密、流动再附长度等几何特征及水力特征多方面对摩阻系数产生影响，并引入了修正系数。

其中，C 为摩阻偏差系数；f0为光滑圆管的摩擦阻力系数；A 表示粗糙元分布的影响，取值为0 到+∞。杜东兴[14]、S. G. Kandlikar 等[15]提出了将粗糙结构对摩阻系数的影响等效为管道内流通面积缩小产生的影响，在此基础上提出了相应模型并加以实验验证。

随着利用数值计算方法研究流体流动特性及流场结构的发展，周健等[16-19]通过细观数值模型对多孔介质流体流动现象进行了模拟并探究其微观机理，结果表明颗粒数值模型能较好地模拟流体和固体颗粒的相互作用，而此次模拟对流体在流场中的流速与压降的分布情况缺乏仔细的研究。李欢等[20]继承了尼古拉兹实验的基本思想，在对管道内壁粗糙度进行模拟时采用了颗粒流程序中的流体计算模块，证明了该模块不仅能对流体和固体颗粒的相互作用进行较好的模拟，而且可以较为真实地反映粗糙圆管模拟过程中流体在圆管中的流动状态。因此，管壁粗糙度对管内流动的摩阻系数影响只存在于流速较大的湍流区。

2 管壁润湿性及其对流动摩阻系数的影响

J. P. Rothstein 等[21-22]讨论了大量的实验数据、计算模型及理论分析的结果，发现在超疏水表面上，水的摩阻系数远低于在普通表面。C.Neto 等[23]评估了近年来关于牛顿流体在固体壁面上的流动情况，认为固体表面粗糙度和润湿性在无滑移边界条件下对流体的摩擦阻力起着主要的影响作用。鉴于上述发展现状，敬加强等[24]建立小型循环管路实验平台并进行了3 种液体分别在4 种不同内壁面材质的管道内层流流动的对比实验，以及使用接触角测定仪分别测量了表面的接触角。得到的结论表明，在液体与管道表面的接触角较大时会使所测液体（自来水、乙二醇、白油）在管道中流动产生的摩阻系数较小，并且在液体与管道内壁面的接触角大于90°；流动状态处于层流区的情况下，润湿性对摩阻系数的影响会更为显著。

2.1 流体与管内壁润湿特性及其影响因素

通常情况下，在液体与固体表面上的三相交点处分别做与气体及固体界面的切线，气液界面的切线与液固界面的切线在穿过液体的方向所夹的角，称为润湿角，也叫接触角，它是衡量固体对特定液体润湿特性的重要指标，主要有四种理论模型。

2.1.1 杨氏模型

其中,θs为静态接触角，也称为本征接触角，γsg为固气界面张力，γsl为固液界面张力，γgl为液气界面张力，J/m2或N/m。作为表面润湿现象的理论基础，杨氏模型通常适用于无限平坦且化学组成均匀的理想固体表面[25-29]。

2.1.2 Wenzel 模型 由于大多数设计用于改变表面粗糙度的表面改性方法也不可避免地改变润湿性。一般而言，表面粗糙度放大了表面的固有润湿性，增强了表面的亲溶性或疏溶性[30]，因此液体在粗糙表面的接触面积大于在理想光滑表面，Wenzel在杨氏模型的基础上引入了表面粗糙度的影响：

其中，θs为表观接触角；r 为表面粗糙度，即粗糙表面的实际面积与其水平投影面积之比。Wenzel 模型建立在液滴能完全浸润到固体表面上的粗糙结构中的假设基础上，并提出了表观接触角的概念。由此可以得到固体，说明表面与液体的润湿性强弱与固体表面的粗糙结构有关。

2.1.3 Cassie 模型 Cassie 模型兼顾了固体表面的疏水性和粗糙结构对液体浸润特性的双重影响，液滴会因为固体表面的较强疏水性而不能满足Wenzel 模型假设的完全浸润到固体表面上的粗糙结构中。因此，固液接触面上还存在着气液接触面，从热力学平衡的角度可以得到：

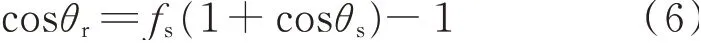
其中，fs为表面面积系数，即与液体接触的固体表面占投影面积的比例。

2.1.4 Wenzel-Cassie 模型 当处于Wenzel 模型及Cassie 模型的中间状态，也就是液体只浸润固体表面上的粗糙结构的一定深度时，则：

其中，x 为液体浸润到粗糙结构中的深度；d 为粗糙结构的凸起直径；b 为粗糙结构之间的间距。

蒋华义等[31]对具有不同粗糙度和表面能的固体壁面以及不同表面张力的液体进行了对比实验，经过线性分析，得出了如下结论：液体表面张力较大时，液体与固体壁面的接触角往往也比较大，而固体表面能的增大则会减小液体与其表面的接触角。与此同时，接触角与固体壁面粗糙度的关系在润湿与不润湿的情况下呈现两种截然不同的变化趋势：当液体与固体表面呈不浸润的关系时，接触角随粗糙度的增大而增大；而当液体润湿固体壁面时，接触角随粗糙度的增大而减小，并且液体表面张力对接触角的影响最显著，粗糙度对其影响最小。

2.2 流体与管壁的润湿性与摩阻系数的关系

研究表明[32-33]，黏附力反映了两相分子间的相互作用力，即固液界面分子的结合能力，表征的是固体和液体分子间的相互吸引力，可以表示为：

其中,γlg是液-气界面张力；Wa是黏附力；θ 是表观接触角。

内聚功Wc为能够在液体中产生界面并将它们分隔成两个独立表面以防止形成蒸气所需要的功，它表征的是液体分子之间相互的吸引力：

所以从微观角度来说，液体黏度及表面张力对其滑移特性的影响归因于液体与固体壁面的润湿特性，而液体与固体壁面的润湿特性取决于液体的内聚力和液体和固体壁面之间的附着力的差值。因此，当管道内流体的内聚力与其和管道表面的黏附力的差很小时，管道内的流体更容易黏附到管道表面，从而导致更大的摩擦损失。这些管道表面的润湿性对相对湿润的管道中的摩阻系数没有影响。而当管道内流体的内聚力与其和管道表面的黏附力的差很大时，此时由于表面接触角很大，流体与管道表面的黏附力很小，与其他管道相比，壁上的一部分液体明显滑动，从而导致较小的摩擦阻力。

结合前人研究，敬加强等[34]分别进行了4 种液体分别在PTFE 管中流动以及自来水在5 种管道中的管流对比实验。实验结果表明，表面润湿性对所研究的宏观管道内流体的摩阻系数有一定的影响，同一雷诺数下摩阻系数随着接触角的增大而减小，并在此基础上建立了两种不同流动情况的摩阻系数与其表面润湿性之间的修正模型：

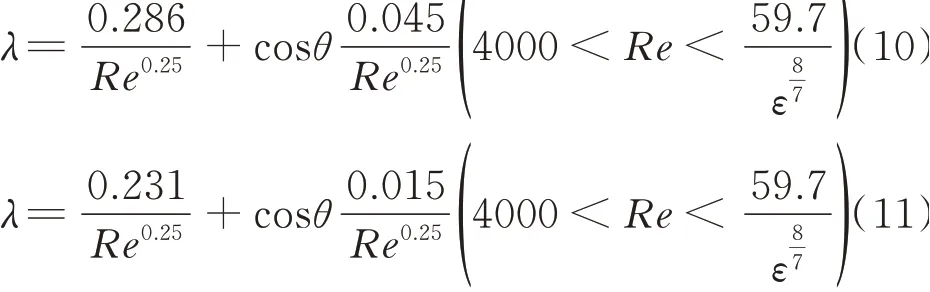
式（10）为自来水在5 种不同管壁材质的管道中流动产生的摩阻系数修正公式；式（11）为在PTFE管道中流动的四种不同流体的摩阻系数修正公式。经两种修正公式得到的摩阻系数与实验值的相对误差均控制在±10%以内。

3 表面滑移效应及其减阻性能的机理

边界滑移通常以滑移长度为特征，滑移长度定义为表面与流体的外推速度等于零的表面内部点之间的距离。因此，表面滑移长度可以用式（12）表示：

其中，us是固体表面上流体的滑动速度；Ls是滑移长度是垂直于表面的方向上的速度梯度。滑移长度一般在Ls=0 和Ls=∞这两种理想情况之间（见图1）。

图1 滑移长度的定义Fig.1 Definition of slip length

因为界面处的液气剪切取代了液固剪切，所以边界滑移归因于固液界面处存在的气体[35-36]。对于Couette 流动，空气层将液体与固体壁分开，这导致在固体表面上流动而几乎没有摩擦。由具有厚度h的纯空气层引起的滑移长度Ls可用式（13）表示[37]：

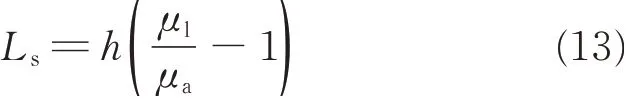
其中，μa是空气的黏度；μl是液体的黏度。从式（13）看出，Ls受液体黏度和表面上空气的影响。因此，超疏水表面上的空气部分对表面滑移效应也是有一定影响的。

由于大多数疏油表面处于亚稳态，故其表面润湿性容易发生改变，因此大多数先前的研究[38-40]使用水作为实验介质。为了构造具有锥形柱的坚固的全非疏水表面，考虑柱的高度b 和锥角2a[41]。基于Laplace-Young 方程，可以使用式（14）、（15）从简单的几何计算中获得表面锥形柱高度b 和插入间距d：

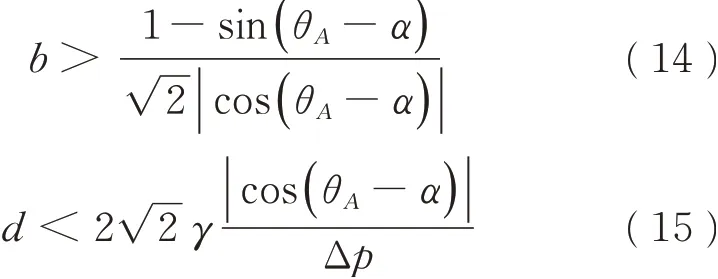
其中，Δp 是液体压力和大气压力的差值，γ 表示液体的表面张力，θA为液体与固体壁面的接触角。两个锥形柱的距离和高度必须满足能够支持液体不接触锥形柱之间底面的标准，也就是说，液体的下垂高度（h1）必须小于最大孔隙深度（h2）（见图2），才能发生边界滑移。C.Lee 等[42]发现液体在双结构硅表面的其微/纳米结构中可以达到98%的气体分数，测得的最大滑移长度远大于传统微光滑疏水硅表面。M. Zhou 等[43]对涂有碳纳米管（CNT）的超疏水表面进行了一系列流变学实验，揭示了表面形态对滑移长度的影响。A. V.Belyaev[44]使用疏水盘进行实验分析了具有较大有效滑移长度的结构化表面。结果表明，边界滑移和摩阻的降低在小间隙的表面结构中尤为明显，并且强烈依赖于气相分数和气体区域的局部滑移长度。基于上述现状，吴阳等[45]在坚固的超疏水阳极氧化铝板上研究了几种低表面张力液体的润湿性，然后通过流变学测量揭示液体和阳极氧化铝表面之间的滑移，得出了液体的黏度和表面张力是滑动长度的重要影响因子。滑移长度随液体黏度的增大而增大，而液体的表面张力越低，下垂高度越高，表面上液体的滑动长度也就越高。

图2 Couette 流动中疏油表面的滑移示意Fig.2 Schematic diagram of slippage of oleophobic surface in Couette flow

高锡祺等[46-47]提出增大流体与管内壁的接触角可以改变管壁处流体边界层的滑移情况，从而达到降低流体在管道内壁的摩阻系数的效果，并且通过不同流体和不同材质管道的对比实验证实了：管道内壁的表面特性改变，致使流体在管内壁上的接触角增大，从而使所输流体不润湿或基本不润湿管内壁。此时紧贴管内壁的位置上原本存在的流速为零的液体边层可能消失并以一定的速度随整个管道内的液体轴向运动。在此过程中，流体边层与管内壁之间会发生相对运动，从而产生额外的摩擦力，但由于液体边层以一定速度向前运动的过程依然会使流体径向流速梯度发生很大变化，从而达到减小沿程摩阻的效果，并且随着管径、液体流速及黏度逐渐增大，沿程摩阻的减小作用更加明显。

郭瑞生等[48]通过在金属表面修饰以可与水表现出不同润湿性的官能团组成的自组装分子为主要结构的涂层来实现不同的润湿特性，通过流变仪及水洞实验分别测量出样品的剪切应力及阻力系数，从而得出层流与湍流条件下的减阻性能，通过对比发现，层流与湍流条件下，润湿性对减阻性能均产生了积极的影响，即润湿角越大，减阻率越高。

经过上述讨论可知，滑移效应的产生与液体和固体材料表面的润湿特性密不可分。所以液、固界面滑移效应是非金属管道流动摩阻规律不同于金属管道的一个重要因素。传统的观点认为，由于液、固界面处的分子间存在非常强的范德华力，导致固液界面处液体分子紧紧黏附在固体壁面上，从而导致了液体与固体之间的无滑移现象。然而，由于液体对其表面的渗透性、范德华力和静电力的存在或者其他一些因素导致非金属管道与无滑移相比更可能存在滑移的情况[49]。

表面滑移现象很显然应该受到表面粗糙度的影响[50-53]，但截至目前，已发表的物理实验中测量滑动幅度的误差较大，使得能表达出两者之间关系的简单图像很难绘制出。但是相对较少的实验研究集中在仅研究粗糙度对边界滑移的影响。这些实验具有挑战性的原因有很多，大体来说可总结为以下几点：（1）难以控制生产合适的表面粗糙度而不会对其他界面性质，例如润湿性，产生预期外的变化，难以将粗糙度和润湿性对表面滑移现象的不同影响分离开来；（2）纳米尺度和微观尺度粗糙度可对表面滑移产生明显不同的影响，对实际表面粗糙度适当且完整的理论描述还尚未发现。然而这方面的模拟结果较为明确，可以帮助指导实验研究。与用于研究复杂表面流动的物理实验相比，模拟的主要优点在于表面的形貌和边界条件的变化是完全已知的。

4 结 论

针对非金属管道摩阻系数较金属管道有很大不同这一现状，从非金属管道管内壁粗糙度、流体与管壁润湿特性及其所引起的表面滑移特性对管内流动摩阻系数影响的研究现状进行总结，得出如下结论：

流体与管内壁之间处于不润湿或基本不润湿的状态时，管壁上不存在流速为零的边层，紧贴管壁的流体分子层以一定的速度沿管轴向运动，进而使流体径向流速梯度大大下降，所以摩阻也将大大下降。而表面滑移长度随液体黏度的增大而增大，与此同时，液体的表面张力越低，下垂高度越高，表面上液体的滑动长度也就越高。因此，在液体与管道内壁面的接触角较大时，液体的摩阻系数通常较小，并且液体不润湿管道内壁面以及雷诺数较小时，润湿性对摩阻系数的影响会更为明显。而管道内壁粗糙度对摩阻系数的影响是从微观粗糙结构、结构之间的疏密度以及由此和润湿性共同作用所引起的滑移效应等多个角度共同作用的。

以水为输送介质时，由于它的疏水性，非金属管道中水与固体壁面形成气体垫层从而引起滑移效应，最后导致摩阻系数的减小；以原油为输送介质时，壁面滑移效应的发生与流体的黏度及表面张力、固体壁面材质的表面能及润湿角是共同影响的，所以原油在非金属表面的状态与其在金属表面的状态相比较，相当于水在金属表面的状态与水在非金属表面的状态相比较，由此可知无滑移理论只是一种理想状态，真实状态下液体在固体壁面上的滑移程度可以通过量化更真实地反映流动状态，从而对摩阻系数做出更符合实际的预测。