变尺度网格法在典型焊接节点应力集中系数计算中的应用

(1.江苏科技大学 船舶与海洋工程学院， 江苏 镇江212003；2.中国船舶及海洋工程设计研究院， 上海200011； 3.上海船舶设计研究院， 上海 201203)

0 引 言

海洋平台是海洋资源开发的基础性设施，也是海上作业和生活的基地。半潜式海洋平台主要由上部平台、立柱和下浮体组成，在远海波浪的长期循环往复作用下，易发生疲劳损坏，尤其是下浮体与立柱相连接的部位焊缝密集，且直接承受波浪力。焊接接头焊趾处截面突变，结构形状不均匀而引起应力集中是导致结构断裂、疲劳损坏的重要原因，并且焊趾位置是疲劳裂纹最易产生的部位[1-2]。因此，对该区域应力集中情况的研究显得尤为重要。

在应力集中系数(Stress Concentration Factor，SCF)的研究中，平台结构较大，常用的计算方式是有限元数值模拟。在数值模拟中，综合运用多种手段建立高质量、高计算效率的模型是1个重要步骤。 网格划分的形式对计算精度和计算时间将产生直接影响。采用分区域多尺度网格法[3]既可保证研究对象的计算精度，又可缩小整个模型的网格规模、减少计算时间、提高效率。目前船舶行业对变尺度网格法的探究较少，可供行业应用的依据也较少，因此针对海洋平台十字节点应力集中处进行变尺度网格法的探究。

1 SCF计算原理

在焊接节点疲劳性能研究中，SCF是评价其疲劳寿命的重要参数。对于无限大平板来说，只要不存在载荷状态集中或形状畸变等部位，就不会产生明显的应力集中和应力峰值。然而，一旦出现破坏这种均匀性的凹洞、突起或材质不均等情况，就再也无法保持应力状态的均匀性，从而引起应力干扰，产生应力集中现象。

通常，用RSCF表示构件的应力集中程度。RSCF可由最大应力或峰值应力σm和基准应力σo的比值[4]表示，即

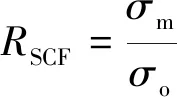
(1)

2 变尺度网格法

分区域变尺度网格法的基本原理是将不均匀网格模型按照网格密度不同划分为多个均匀的网格模型[3]。在决定网格疏密度时考虑计算数据的分布特点和工程需要：在计算数据变化梯度较大的部位(如应力集中处)，为了较好地反映数据变化规律，应加密网格；在计算数据变化梯度较小的部位，为了减少计算时间，则应疏减网格。本文针对十字焊接节点进行静力分析，计算SCF数值。

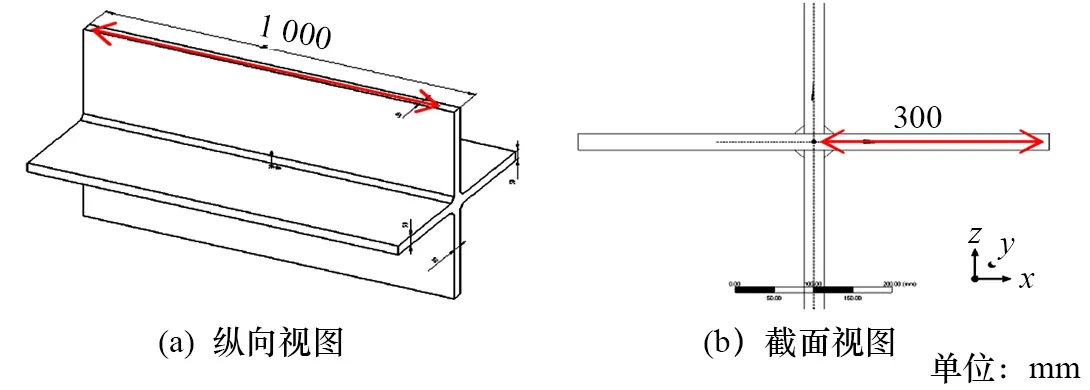
图1 体单元结构模型

2.1 有限元模型

基于ANSYS WorkBench(WB)软件建立体单元结构模型，模型尺寸板均为1 000 mm×300 mm，板厚均为25 mm，如图1所示。只对焊接结构形式的应力集中情况进行模拟研究，因此在建立有限元模型设置参数时，将焊缝与板设置成同一种材料属性，材料属性为弹性模量2.0 GPa、泊松比0.3、密度7 580 kg/m3，结构板厚T均取25 mm，长为1 000 mm。

针对图1所示模型，参考DNV-GL规范[5]，十字横向角焊焊接节点在焊趾处发生应力集中时的RSCF标定值为1.43。

2.2 网格划分方法

为得到具体的适合体单元模型计算SCF的网格密度过渡方法，将网格划分如下：首先利用WB软件对模型进行前处理，将焊缝区域分割出来，采用较密的网格密度；然后在焊缝的基础上，向外划分一段过渡区域，本文选择的两种过渡是2T和4T距离，此处的网格密度为过渡作用；最后将过渡区域以外的模型结构单独分割出来，划分为较粗的网格密度。需要注意的是，区域分割出来之后仍然要合成一个整体。

为了探究变尺度网格划分方法的优越性，采用常用的网格划分方法即全局网格划分和局部细化网格划分作对比。具体划分方式如表1所示。

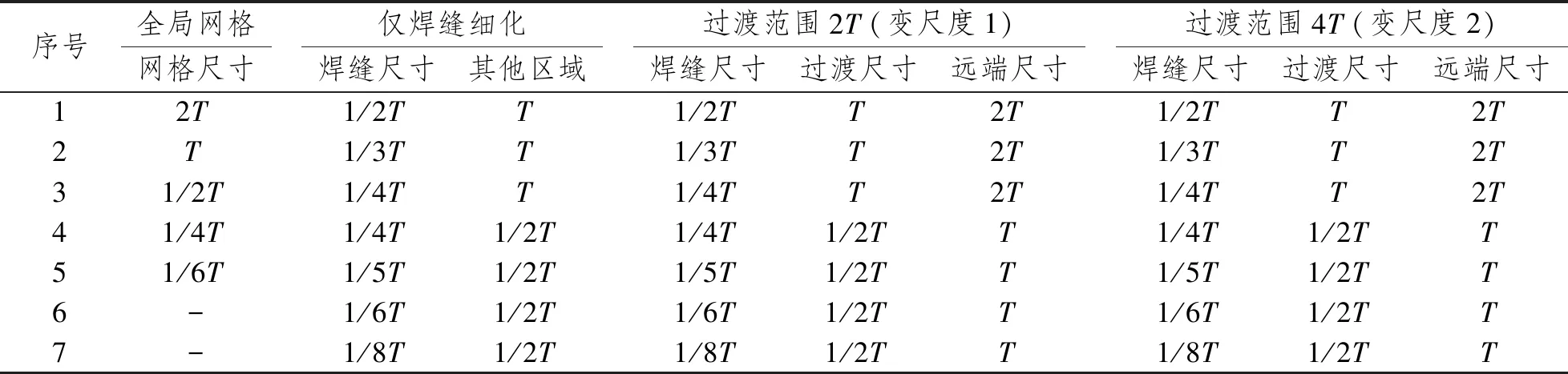
表1 多种网格的划分方式

2.3 计算结果初步对比

根据表1的划分方法进行网格划分，分别计算SCF，将计算结果初步进行统计对比。首先考虑计算结果稳定性，将全局网格法、仅焊缝细化法和变尺度1进行比较，如图2(a)所示。其次，考虑计算结果准确性，针对采用区域细化的3种方法，将计算结果与标定值进行对比，如图2(b)所示。

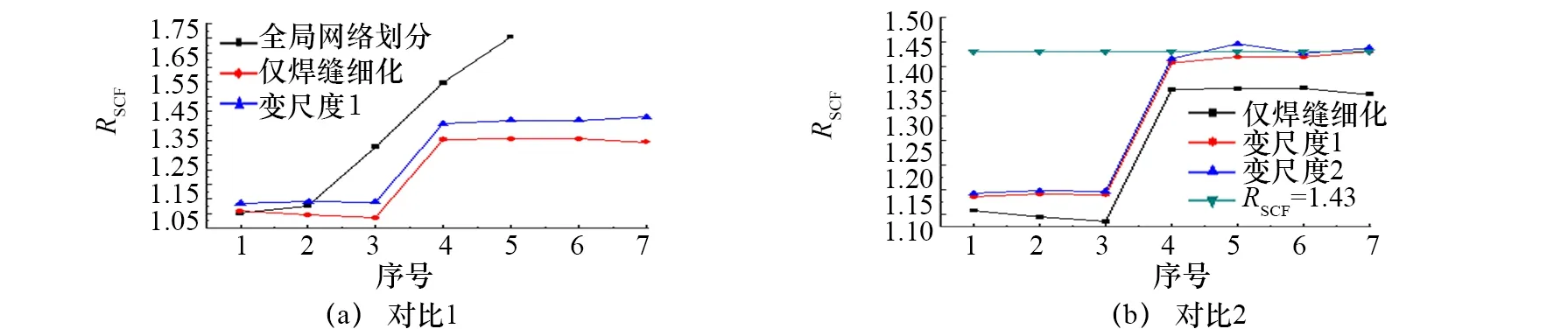
图2 多种网格划分方法计算结果对比

由图2(a)可知：网格密度对计算结果的影响十分显著，特别是全局网格划分方法存在着较大的弊端，随着网格密度的变化，计算结果之间差距很大。在应力集中现象的许多研究中，往往采用将应力集中区域进行细化的方法计算热点应力或SCF。仅焊缝细化网格和变尺度网格划分方法都是细化划分网格方法之一，从图2中可较明显地看出，细化之后计算结果在一部分过程中是趋于稳定的。由此可见，对热点区域细化是有效控制计算结果的一种方法。

图2(b)针对细化方法将计算结果进行对比，显然这3种细化方法都存在两个阶段，计算结果在每个阶段内趋于稳定，在阶段之间差距较大。同时，采用变尺度的两种方法在网格细密的第二阶段具有较为准确的计算结果，误差最大为1.59%，最小为0.04%，满足工程计算需要。

2.4 网格质量优化

根据图2(b)所示结果，3种细化方法的两个阶段可能是由网格质量引起的[6-7]，如图3所示。将区域划分方法进行调整，将焊缝包围区域作为1个梯形整体，按照表1焊缝网格密度进行划分。

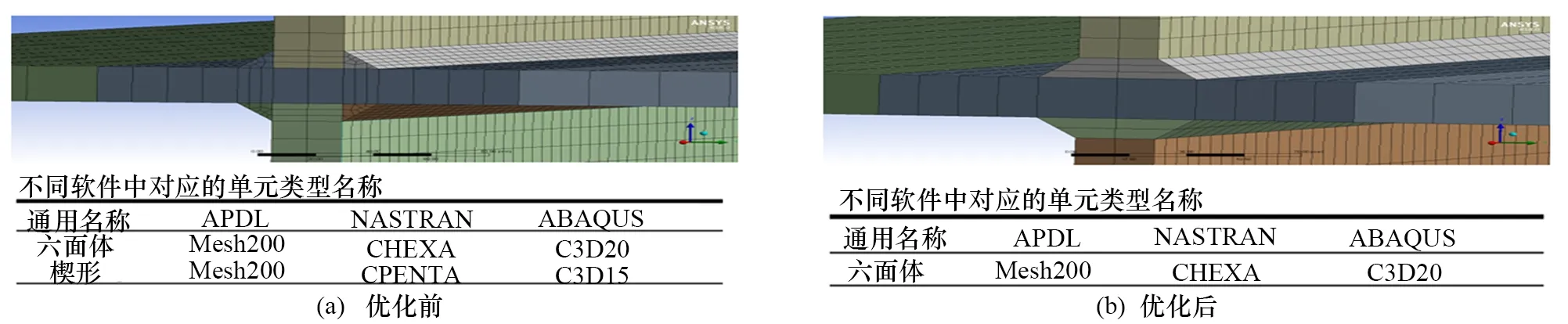
图3 3种细化方法优化前后网格划分情况

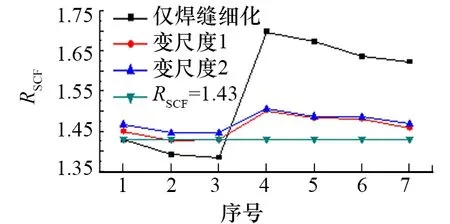
图4 网格质量优化后计算结果对比

优化前网格存在大量六面体单元和少量四面体单元，优化后所有网格均为六面体单元。网格质量优化后，计算结果有了显著变化，如图4所示。在优化后，3种细化方法的第一阶段计算值均变大，并接近标定值，但是仅采用焊缝细化的网格划分方法，计算结果的变化曲线依然呈现两个跳跃式阶段，说明这种划分方法计算结果的波动依然较大。采用变尺度网格法的两种方案的计算结果趋势基本一致，且与标定值的误差最大为5.21%，在7种设计方案中方案1、方案2、方案3的计算结果与标定值的最大误差为2.39%，满足工程计算的要求。由此可见，变尺度网格法不仅计算结果稳定性好，而且计算结果准确性更高。

2.5 计算结果对比

通过初步的计算结果对比和优化网格质量后的计算结果对比发现，变尺度网格法计算精度高、计算耗时短，而变尺度网格法的关键在于过渡阶段的网格密度以及过渡网格的范围大小的设置，其直接影响计算精度和计算时间。将变尺度方法计算结果进行统计对比，如表2所示。

表2 变尺度网格法计算结果对比

由表2中数据统计可知，在过渡网格密度和范围一定时，焊缝网格越细密，结果越准确。在过渡网格密度为1/2T+T时，两种变尺度法的计算结果趋势基本一致，呈收敛趋势，即将网格密度进一步减小时，计算结果应该更接近标准值。在过渡网格密度为T+2T时，计算结果已接近标定值，网格在此加密，结果已经呈现稳定状态；在过渡范围为2T时，计算最大误差为1.32%；在过渡范围4T时，最大误差为2.59%。因此，在十字焊接节点体单元模型计算SCF的分析中，采用从焊缝区域、过渡区域、远端依次按照0.25T，T，2T的网格密度进行网格划分，过渡范围为2T的方法进行计算，计算精度高且计算耗时少。

3 总 结

以第七代半潜式海洋平台设计制造为工程背景，为应对非连续变形结构分析中出现的计算精度和计算时间问题，探究变尺度网格法在计算SCF中应用的优越性，得出结论如下：

(1) 在十字焊接节点体单元模型计算SCF的分析中，采用从焊缝区域、过渡区域、远端依次使用0.25T，T，2T的网格密度进行网格划分，且过渡范围为2T的网格划分方法进行计算，计算精度高，且计算耗时少。

(2) 为计算一些细节应力集中问题，在有限元划分网格时，不必用密度特别小的网格，导致网格数量巨增、计算效率变低，且计算数据误差大。建议采用变尺度网格划分方法进行计算，计算效率高且计算结果较为准确。

(3) 网格质量也是影响计算结果的一个重要因素，网格质量的好坏决定了计算结果的准确性，从工程计算角度分析，网格质量优时计算出的结果具有较高的参考价值。