两种比较模型预测效果的评价指标及其R实现*

李彤阳，林卓琛，葛琪，陈雯，张晋昕

510080 广州，中山大学 公共卫生学院

在医学研究特别是临床医学研究中，Logistic回归是常见的分析方法[1-2]。以两分类logistic回归为例，模型的因变量为患病与否，自变量为一系列与该病相关的指标。通过建立Logistic回归模型我们可以通过每个观察对象的疾病相关指标，计算出其患病预测概率。目前，Logistic回归在临床肿瘤患病风险研究中应用广泛：如基因多态性与食管癌患病风险关系研究[3]，2型糖尿病并发恶性肿瘤风险研究[4]，以及卵巢肿瘤良恶性的鉴别诊断[5]，也有癌症术后不良反应发生率及其相关危险因素的研究等[6-7]。

在实际研究中，如果涉及到两个Logistic模型预测效果的比较，例如两种诊断试验的比较，或是在常规影响因素中添加某一新的生物标志物或感兴趣的危险因素，我们常比较两个模型的灵敏度、特异度、准确度、受试者工作特征(receiver operating characteristic，ROC)曲线[8]以及曲线下面积(area under curve，AUC)[9-10]。通常，Logistic回归会给出模型的分类表，据此可以看到两个模型各自的灵敏度、特异度、准确度等指标，若是想进一步整体比较两模型孰优孰劣，则需比较AUC。 AUC综合了ROC曲线上所有点作为诊断截点的情况，直观地反映试验的整体预测效果，在临床上尤其是诊断试验的比较中应用广泛。但在实际应用中，我们常常更关注某一诊断截点下两个模型对个体的分类能力，这时AUC就不那么好用了；此外，AUC的敏感性有时并不强，其增量并不明显，专业意义也不易理解[11-12]。如果我们关心新模型相比于旧模型，对于个体的预测概率改善了多少，或是判断新加入的生物标志物是否影响到临床决策，那么只采用常规的方法就不够了。近年来，其他比较新旧模型预测效果的方法相继提出，其中运用最多的是Pencina提出的净重新分类指数(net reclassification improvement，NRI)和整体鉴别指数(integrated discrimination improvement，IDI)[11,13-15]。NRI关注的是在诊断截点处，通过考察使用新模型后个体预测概率的变化情况，或个体被重新分类的情况，得出新模型比旧模型使得不同组别个体更有利于分到正确组的概率，并对两组预测概率的改善求和而IDI则是使用两个模型预测概率均值的差来整体评价新模型改善的程度，故NRI和IDI更贴合应用需求[11,13-14]。

1 NRI和IDI的意义与计算

1.1 常用的模型评价指标

在Logistic回归模型中，由自变量计算预测概率，当预测概率大于某截点值时，可认为该观察对象属于1组，否则属于0组。而根据课题研究背景，常以1代表患病(y=1)，0代表不患病(y=0)，此时我们就可以认为预测概率高于该截点时，该观察对象被预测为患病组(反之被预测为不患病组)。

通过诊断试验四格表可以计算出灵敏度、特异度、约登指数等一系列指标。灵敏度为患病组中个体被正确预测为患者的概率，特异度为不患病组中个体被正确预测为健康者的概率，约登指数为灵敏度与特异度之和减去1。

另外，根据连续型变量(如预测概率)截点大小的选取，得到的灵敏度和特异度也会相应地改变，这种变化通过连线的形式呈现出来就是ROC曲线，计算ROC曲线下面积则可以得到AUC值，它是对连续型变量无固定截点时预测能力的概括性刻画。

1.2 NRI指数

净重新分类指数NRI[11,13-15]，评价的是在两模型采用最优诊断截点进行预测时，与旧模型相比，使用新模型使得个体的预测结果得到改善的概率，包括事件发生组改善概率与不发生组改善概率两部分(在R中分别以NRI+和NRI-表示)。R中对于NRI指数的计算有两种不同的方式，一是将预测风险概率视为连续变量，对应于R中的diff方法；一是将风险概率划分为若干区间，对应于R中的category方法。

1.2.1 diff法NRI指数 diff法NRI指数以某一概率变化值(概率变化的大小，而非概率截点)作为判断新旧模型预测概率变化的依据，只要个体的预测概率变化超过了某一变化值，例如0.02，则认为该个体在新模型下预测的概率和旧模型的不同。相应的的计算公式如下：

NRI=P(up|event)-P(down|event)+
P(down|nonevent)-P(up|nonevent)

(1)

为了便于理解这个公式，我们以预测结局为患病、不患病两种情况的研究为例，其中up|event和down|event分别表示患病组中个体采用新模型后预测概率值上升和下降的情形(概率变化的幅度超过了设定值才认为是上升或下降)，down|nonevent和up|nonevent表示不患病组中，个体采用新模型后预测的概率值下降和上升的情形(上升和下降的定义同前)，并分别对应于各情形发生的概率。在实际计算中，可以使用以下公式计算NRI指数：

(2)

其中#up_event和 #down_event 分别表示患病组中新模型预测的患病概率上升和下降的人数(上升和下降的定义同前)，相应的，#up_nonevent和#down_nonevent分别表示不患病组中新模型预测的患病概率上升和下降的人数(上升和下降的定义同前)。#event表示患病组人数，#nonevent表示不患病组人数。

由上述公式可知，NRI指数越大，则与旧模型相比，在新模型中个体无论是本来属于患病组还是不患病组，均有更大机会被分至实际所属的组别，预测结果的正确率得以提高，使用新模型后患病组计算出来的预测概率(P(y=1))更高了，而不患病组计算出来的预测概率(P(y=1))更低了。

1.2.2 Category法NRI指数 Category法NRI指数是将预测风险概率以若干个概率截点划分为感兴趣的概率区间，并基于一个重新分类表，考察个体被新模型预测后重新分类到不同概率区间的情况，它不关注个体概率变化了多少，而是直接分析个体发生某事件的预测概率所属的区间类别得到优化的概率。仍以预测结局为患病和不患病的研究为例，当仅设置一个概率截点时，由于实际上是将概率区间二分类了，其重新分类表相当于一个患病组和不患病组分开统计的配对四格表(见表1)，可按公式(3)计算NRI指数：

(3)

表1 二分类category法NRI指数新旧模型预测结果的重新分类表

Table 1. Reclassification Table for Category-Based NRI with One Cut-off

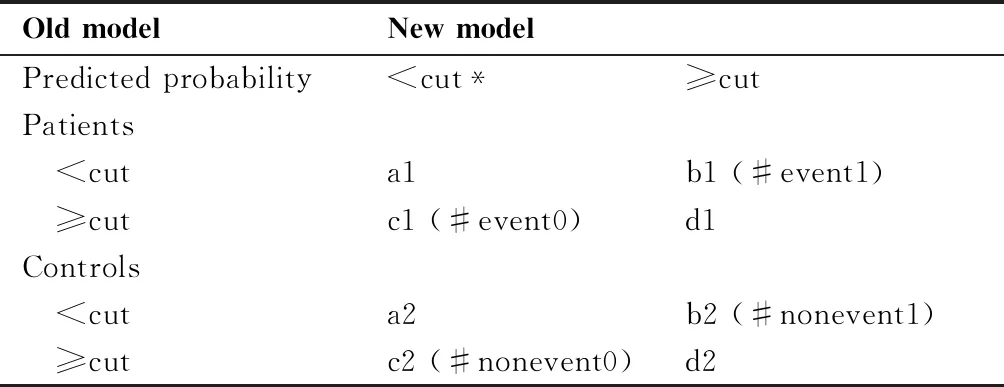
Old modelNew modelPredicted probability

*Cut: Probability cut-off.

结合公式(3)和表1，#event1和#nonevent0分别表示患病组和不患病组中新模型预测正确而旧模型预测错误的人数(b1和c2)，#event0和#nonevent1分别表示患病组和不患病组中新模型预测错误而旧模型预测正确的人数(c1和b2)。#event表示患病组人数，#nonevent表示不患病组人数。可见，由于a1，d1，a2，d2是两种模型预测的概率区间相同的情况，在计算NRI指数时并未用到。

同时不难发现，此时category法的NRI指数等于新模型灵敏度与特异度之和减去旧模型灵敏度与特异度之和，在数值上也相当于新模型的约登指数减去旧模型的约登指数。

当我们设置多个概率截点时，模型预测的风险概率就被划分成不同的概率区间(规定新旧模型的预测概率区间采用相同的划分方式)，此时我们认为患病组和不患病组个体患病风险概率的分布不同，理论上患病组的人更多地集中在风险概率高的区间，不患病组的人更多地集中在风险概率低的区间，因为模型计算出来的预测概率越大，越有利于该个体预测为患病，同理，模型预测的概率越小，越有利于个体被预测为不患病。此时NRI指数计算公式的形式与公式(2)相同，含义略有差别：

公式中#up_event和#down_event分别表示患者采用新模型预测后所属的概率区间比旧模型预测的概率区间等级升高和降低的人数， #up_nonevent 和#down_nonevent分别表示不患病者采用新模型预测后所属的概率区间比旧模型预测的概率区间等级升高和降低的人数，相应的重新分类表(以设定2个概率截点为例)见表2，其中x1，x5，x9；y1，y5，y9表示预测结果相同的情形。实际上，公式(2)用在此处，仅仅是升高和降低的含义发生了改变，在diff法中升高和降低的前提是个体预测概率的差值超过了设定的概率变化值，在category法中升高和降低的判断是依据个体所属概率区间等级的改变。另外，category法中只设定一个概率截点的情形也适用于公式(2)，相应含义与设定多个概率截点时相同。

表2 三分类category法NRI指数新旧模型预测结果的重新分类表

Table 2. Reclassification Table for Category-Based NRI with Two Cut-offs

Old modelNew modelPredicted probabili-ty

*Cut: Probability cut-off.

1.2.3 NRI指数的假设检验 对于Category法NRI指数，可以使用公式(4)计算其对应的z值，实施总体NRI指数是否等于0的假设检验[13]，其中#up_event、#down_event、#up_nonevent 和 #down_nonevent取category法使用公式(2)时对应的含义。

(4)

而对于diff法的NRI指数，可使用Bootstrap(自助)法算出其对应的置信区间和P值。

1.3 IDI指数

1.3.1 IDI指数的定义与计算 整体鉴别指数IDI[11,13-14]，或称综合判别改善指数，它考虑了不同诊断截点的情况，并且从平均概率的角度反映了模型的整体改善状况。计算公式如下：

(5)

由公式(5)可以发现，基于预测概率越高越可能为患病组的设定， IDI指数越大，说明新模型可使两组个体被判定为本应所属类别的指向性更明确，鉴别能力得以提高。

2 实例分析

本文采用《SPSS 8.0 for Windows统计软件使用指南》[16]中Logistic回归分析章节50例急性淋巴细胞白血病病人资料(文中例14.3)。数据共包含5个变量，其含义分别为：X1：入院治疗时取外周血中白细胞数(千个/mm3)；X2：浸润淋巴结分级(根据浸润程度分0，1，2 三级)；X3：治疗缓解后病人有无巩固治疗(有=1，无=0)；t：随访病人生存时间，按月计算；研究结局Y：病人生存时间是否小于1年(一年或以上=0，一年以下=1)。本次研究目的是建立合适的Logistic回归模型，对淋巴细胞白血病一年内是否死亡进行预测。现分别建立两个模型，其中模型1纳入自变量入院治疗时取外周血中白细胞数和浸润淋巴结分级，模型2在模型1自变量的基础上再加上治疗缓解后病人有无巩固治疗，模型建立后使用NRI与IDI对两模型预测效果进行评价。

在R中可使用nricens包和PredictABEL包进行指标的计算，相应的R代码如下：

#读入需要使用的包

#install.packages("PredictABEL")

# install.packages("nricens")

library(PredictABEL)

library(nricens)

#建立计算最佳截点函数

opt.cut=function(perf, pred){

cut.ind=mapply(FUN=function(x, y, p){

d=(x-0)^2+(y-1)^2

ind=which(d==min(d))

c(sensitivity=y[[ind]],specificity=1-x[[ind]],cutoff=p[[ind]])

}, perf@x.values, perf@y.values, pred@cutoffs)

}

#读取数据

setwd("D:data")

dat<-read.csv("data.csv",na.strings="#NULL!")

#拟合模型

mod1<-glm(y～X1+X2,family=binomial(link=′logit′),data=dat)

mod2<-glm(y～X1+X2+X3,family=binomial(link='logit'),data=dat)

pre1<-predict(mod1,newdata=dat,type='response')

pre2<-predict(mod2,newdata=dat,type='response')

pred1<-prediction(pre1,daty);pref1<-performance(pred1,"tpr","fpr")

pred2<-prediction(pre2,daty);pref2<-performance(pred2,"tpr","fpr")

cutpoint1<-opt.cut(pref1,pred1)[3];cutpoint2<-opt.cut(pref2,pred2)[3]

pre_case1<-pre1>cutpoint1;pre_case2=pre2>cutpoint1

table(daty,pre_case1);table(daty,pre_case2)

#使用nricens包计算NRI指数

updown="category",cut=cutpoint2,niter=10000,alpha=0.05)

updown="diff",cut=0,niter=10000,alpha=0.05)

#使用PredictABEL包计算NRI指数和IDI指数

reclassification(data=dat,cOutcome=5,predrisk1=pre1,

predrisk2=pre2,cutoff=c(0,cutpoint2,1))

结果如表3和表4：

表3 基于是否考虑“有无巩固治疗”所得两模型预测概率的重新分类表

Table 3. Predictive Probabilities of Two Models With or Without the Consolidation Therapy Variable

Model 1Model 2Predictive probability <0.825≥0.825Death within 1year (n=30) <0.825821 ≥0.82501Survival >1 year (n=20) <0.825182 ≥0.82500

本例中选取的概率截点0.825，是通过拟合模型预测概率的ROC曲线，并取约登指数最大值对应的概率确定的。如果已经确定好概率截点，可直接给出相应的赋值。表3相当于二分类category法NRI指数的重新分类表。读者也可据表3按公式(3)计算NRI(category)，结果与表4中软件计算的值相同。此外，结果报告时还应给出一年内死亡与未死亡组各自的概率的改善[15]，这与R输出组与NRI+和NRI-对应(此处以略)。

由表4可知，两个R软件包计算的NRI指数结果一致， nricens包没有提供IDI的计算结果；实际上两个软件包都会给出相应的置信区间，此处受篇幅限制未列出。由表4可知，模型2(包含“有无巩固治疗”的模型)与模型1(不包含“有无巩固治疗”的模型)相比，得到的NRI指数和IDI指数均为正数，即模型2的分类能力优于模型1，也即，包含“有无巩固治疗”的模型比不包含的模型分类能力好。具体好在何处？以category法NRI指数为例，值为0.600，说明使用模型2相对于模型1，使得一年内死亡和未死亡的患者更有利于得到正确分类的概率之和为0.600(注意，此处不可理解或表示为百分比或概率[15]),P<0.001，结果具有统计学意义；类似地，IDI指数是0.298，说明采用模型2相比于模型1，在一年内死亡组(Y=1)中预测患者一年内死亡的概率均值的提高量和在一年内未死亡组(Y=0)预测患者一年内死亡的概率均值的降低量之和为0.298，说明模型2预测能力比模型1要好，P<0.001，可见结果具有统计学意义。

表4 基于是否考虑“有无巩固治疗”所得两个统计模型的比较

Table 4. Two Statistical Models With or Without the Consolidation Therapy Variable

Software packageNRI (category)PNRI (diff)PIDIPnricens0.6002.00×10-81.1671.95×10-07———*———*PredictABEL0.6001.11×10-81.1671.39×10-070.2982.93×10-6

NRI: Net reclassification improvemen; IDI: Integrated discrimination improvement.

* No corresponding results provided.

3 讨 论

生物医学数据中经常用到Logistic回归模型来对疾病发生进行预测。除常见的灵敏度、特异度、约登指数、AUC等指标外，NRI指数和IDI指数也可用于评价模型预测的效果，且是全面的定量分析指标。R软件提供的nricens包和PredictABEL包能方便地实现计算。

ROC曲线与AUC值刻画了模型在选用不同诊断截点时的灵敏度和特异度，AUC的提高通常可作为模型预测能力改善的第一判断标准，然而实际应用中，当两个模型的AUC曲线存在交叉时，或AUC的增量极小时，仅仅采用AUC可能就很难说明问题了，此时NRI和IDI指数则是更好的选择。当设置了一至多个概率截点，关心截点处的分类情况时， category法的NRI指数就更合适，如果目前还无法确定明确的截点，或需整体评价两模型的预测能力，则IDI指数和AUC更适合[11]。

本文中虽然给出了两种计算NRI指数的方法，但是实际应用中通常采用category法，即给出概率截点划分预测概率区间，并以此作为个体分类的依据。由于category法NRI指数的计算与设定的概率截点有关，因此，预测概率区间的划分应该选择适宜的界值，需要结合临床专业的需求来确定。区间划分不恰当时，可能得不到统计上有意义的结论，或者所得结论缺少临床实践的指导意义[11];同时，由于计算时只考虑了已调变化，未考虑变化的等级数，因此可能存在信息缺失[12];这可能是NRI指数使用存在的缺陷。此外，在模型比较时，需注意概率截点选择的侧重点是否一致，比如有的模型以提升特异度为侧重点，有的模型以提升灵敏度为侧重点，这就需要在使用NRI和IDI指数的过程时考虑两个模型的“侧重类型”是否相同，侧重类型不同的模型间没有可比性。当前研究大多数研究考虑灵敏度和特异度各占一半的比重，但某些特殊的模型例如用于初筛的模型则偏重灵敏度，因此在模型的评价上需更加谨慎的应用NRI和IDI指数[17]。对于IDI指数来说，在计算总改善情况时，通常患病组和不患病组占有同等的比重，但对于侧重于灵敏度的模型，计算时应给予患病组概率改变量更多的权重。对此类模型，可以使用调整过权重后的IDI。有兴趣的读者可做进一步的研究[18]。

理论上，除了将NRI和IDI指数应用在Logistic回归模型外，也可应用于其他可以输出预测概率的模型，如决策树、随机森林、神经网络等。但是对于这两个指标在这些模型中的适用性，仍需进一步的研究与讨论。

综上，NRI和IDI指数是近年来新兴的模型比较评价指标，在模型比较中能够轻松处理AUC等不能解决的复杂情形，具有独特的优势，但二者在肿瘤流行病学研究中应用还较少。本文结合临床肿瘤风险预测实例，详细阐述了两种指标的计算原理和适用情况，以及使用R语言计算两种指标估计值及假设检验的方法，以期为临床肿瘤研究工作者提供更为详尽的参考。当涉及两模型优劣的比较，或考察某一因素的加入对模型预测效果的改善程度时，除了使用约登指数及AUC外，建议研究者不妨同时考虑NRI和IDI指数，以期更加全面地展示模型的改善情况。

作者声明：本文全部作者对于研究和撰写的论文出现的不端行为承担相应责任；并承诺论文中涉及的原始图片、数据资料等已按照有关规定保存，可接受核查。

学术不端：本文在初审、返修及出版前均通过中国知网(CNKI)科技期刊学术不端文献检测系统的学术不端检测。

同行评议：经同行专家双盲外审，达到刊发要求。

利益冲突：所有作者均声明不存在利益冲突。

文章版权：本文出版前已与全体作者签署了论文授权书等协议。