非配对设计二值资料多水平多重Logistic回归分析

刘红伟，张甜甜，李长平，2*，胡良平

（1. 天津医科大学公共卫生学院卫生统计学教研室，天津 300070；2. 世界中医药学会联合会临床科研统计学专业委员会，北京 100029；3. 军事科学院研究生院，北京 100850

*通信作者：李长平，E-mail：1067181059@qq.com）

1 基本概念

1.1 二值资料

结局变量只有两个取值的资料称为“二值资料”，例如，在表1多中心临床试验数据中，治疗结局取值为“成功”或“失败”。

1.2 多水平数据

多水平数据或具有多水平层次结构的数据是多水平统计模型发展和应用的基础。多水平数据也就是自然形成的层次数据，例如，在多中心临床试验中，每个中心是水平2 单位，受试者是水平1 单位；在动物试验中，小鼠是水平1单位，窝别是水平2单位。多水平数据具有非独立性，故无法采用广义线性模型进行分析，因此提出了能够处理多水平数据的多水平模型［1-2］。

与广义线性模型相比，多水平模型稍显复杂，因为它同时包含了多个水平的数据，从而在多个水平上都存在残差。总体来说，其建模的思想就是把高水平上的差异估计出来（传统的线性模型不考虑这一差异，将其放到了一个统一的残差中），就使得残差变小，估计的结果更可靠［3-4］。

虽然理论上多水平模型可以有多个层次，但实际中最常用的是二水平模型，因此这里主要通过一份二水平数据简要介绍多水平模型构建与求解的思路。

2 数据结构

【例1】某地区开展多中心临床试验，拟比较两种药物治疗某疾病的效果。数据见表1。

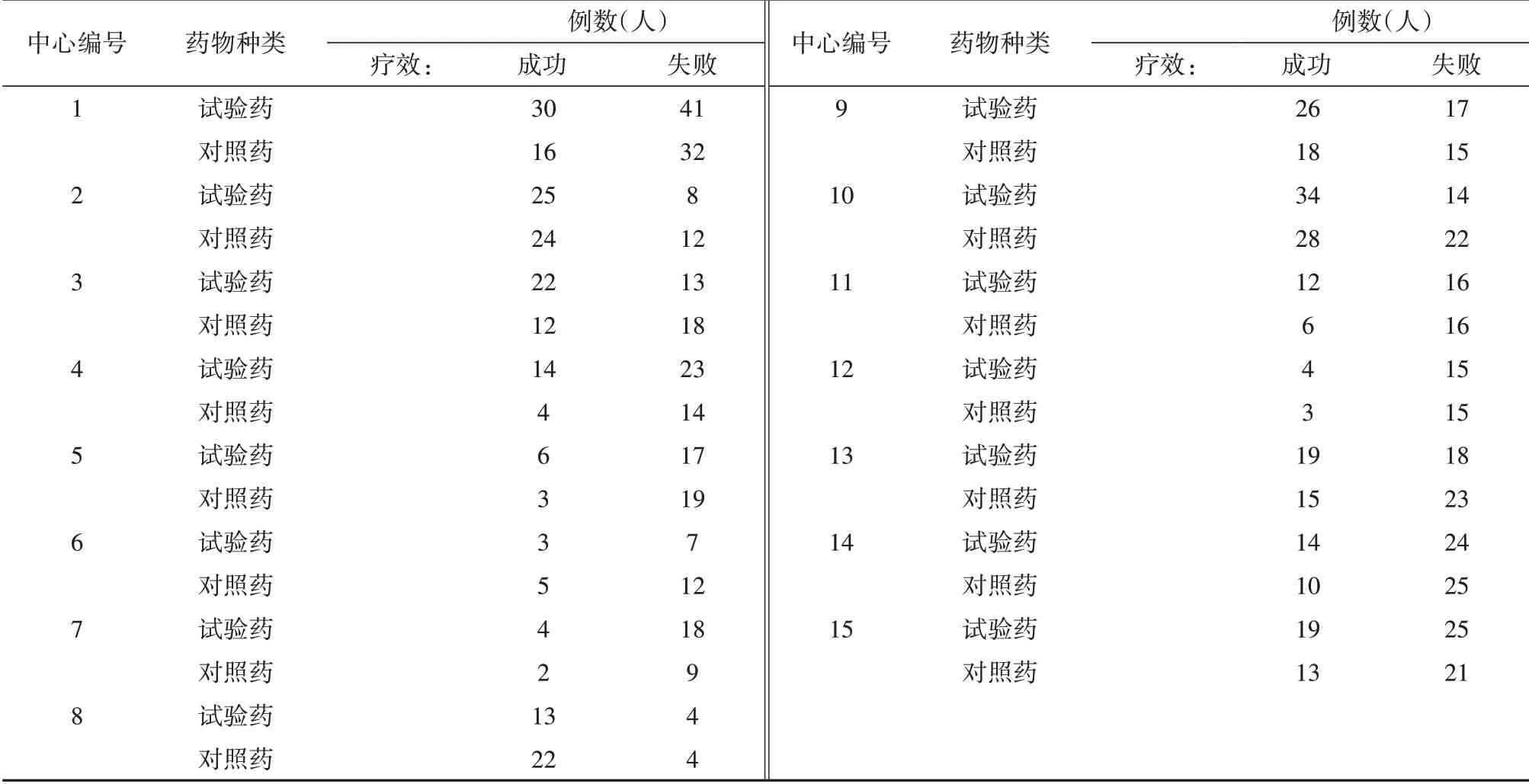
表1 多中心临床试验数据

3 非配对设计二值资料多水平多重logistic回归模型的构建原理

3.1 回归模型的表达式

对于响应变量为二值变量的非层级结构数据，一般采用普通logistic 回归模型分析，又称为固定效应logistic回归模型分析。设P（y=1|X）（简记为P）表示暴露因素为X 时个体发生阳性事件（以y=1 表示发生阳性事件）的概率，而阳性事件发生的概率P与阴性事件发生的概率（1-P）之比称为优势比。对优势比进行自然对数变换即为对P的logit变换，得：

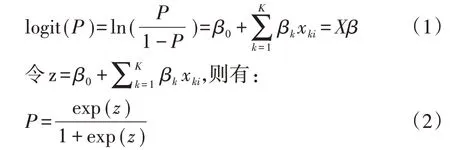
对于响应变量为二值变量的层级数据结构，可采用多水平logistic回归模型分析，其模型可表达为：

其中，U是随机回归系数向量，服从N(0，G)，G为协方差矩阵，β是水平1固定回归系数向量，X和Z分别是固定效应和随机效应的解释变量设计矩阵。

3.2 回归模型的构建

以例1 为例，以变量zhongxin 表示“中心”，以变量drug 表示“药物种类”，以变量y 表示疗效（y=0 表示治疗成功，y=1表示治疗失败），以Pij表示个体y=0发生的概率。建模过程如下：

第一步，建立空模型，计算组内相关系数ICC的值。空模型中仅有一个随机截距而不包含任何解释变量，其模型为：，上述模型可合并为：

其中，βo为y=0 的总平均logit 值，μ0j为组水平（本资料为中心）的平均logit 值的变异量，表示第j个组的平均logit值与总平均logit值之间的差异，且。多水平logistic 回归模型的组间变异也可用组内相关系数进行评估，因logistic 回归模型的残差方差为π2∕3，所以：

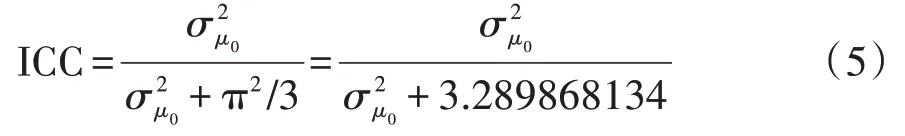
第二步，建立包含解释变量的随机截距模型，即在随机截距的基础上再考察变量drug 的固定效应。模型如下，上述模型可合并为：

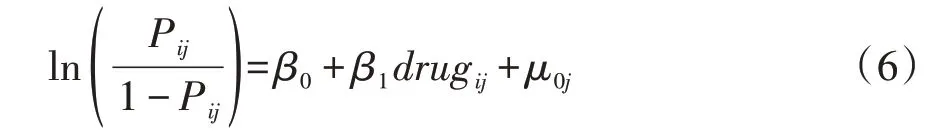
其中，β0j+β1drugij为固定效应，μ0j为随机效应，且。

第三步，建立包含解释变量的随机截距-斜率模型，即截距项和解释变量drug 的系数均为随机系

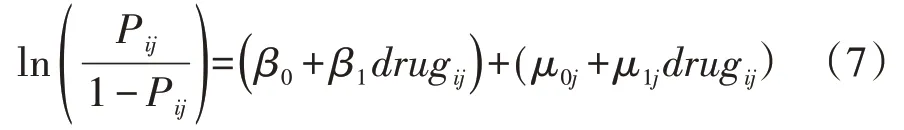
其中，β0+β1drugij为固定效应，μ0j+μ1jdrugij为随机效应，且，μ0j与μ1j之间的协方差可能有统计学意义；若无统计学意义，则将它们之间的协方差设为0。

例1较为特殊，其最终模型是包含解释变量drug的随机截距模型，但又与第二步所建模型略有不同，区别在于本资料截距项为0，即βo=0。例1 的最终模型中包含一个固定效应和一个随机效应，模型如下：

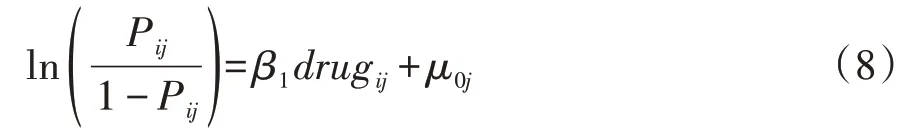
4 基于SAS分析实例

4.1 分析与解答

在例1中，研究者欲考察试验药与对照药治疗某种感染的效果。资料中涉及两个原因变量——中心和药物种类，响应变量为二值变量，由于不同医院对同一疾病的治疗效果可能有差异，而在同一医院中，相同疾病的治疗效果也并不完全独立。故可考虑采用多水平logistic回归模型分析，SAS程序如下：

【说明】程序共5步，包括1个数据步和4个过程步。程序第2 步、第3 步是建立不包含任何解释变量的空模型，以计算ICC 值。程序第4、5 步均是建立包含解释变量drug 的随机截距模型。GLIMMIX过程的计算结果与NLMIXED 过程的结果会略有差异，前者运算速度快、用法简单，但在评估模型拟合效果时使用虚拟的对数似然值，而非真实值，不能用于模型的比较，且SAS 9.4 的中GLIMMIX 过程没有提供随机效应的假设检验，其结果虽有随机系数方差的参数估计值及标准误，但两者的比值只能作为参考，不能采用t 检验计算相应的P 值。NLMIXED过程可以提供真实的对数似然值，并为随机效应提供假设检验的结果，也可以通过似然比检验对嵌套模型的拟合效果进行比较，但其用法较复杂，需设置模型和参数的初始值，不便于使用。因此一般以GLIMMIX 过程得到的参数估计值作为NLMIXED 过程的模型参数初始值，最后以NLMIXED 过程的结果为准。对于相对简单的模型而言，NLMIXED 过程对参数初始值并不敏感，此时采用其默认的初始值1 即可。调用NLMIXED 过程运行包含解释变量的随机截距-斜率模型，所用程序与本节程序第5 步有较大修改。参考程序如下：

其中，“b0”“b1””v_u0”“cov_u01”“v_u1”分别相当于公式（7）中β0、β1、μ0j的方差，μ0j与μ1j之间的协方差，μ1j的方差。

【主要输出结果及解释】以下是第一个过程步输出结果，即调用GLIMMIX过程运行空模型。模型构建是以”y=0”为基础的，即计算”y=0”发生的概率模型。

以上是模型拟合的有关信息，第一行即为-2 倍的限制性∕残差虚拟对数似然值，此统计量不能用于不同模型的比较。

以上是协方差参数估计的结果，给出了随机效应方差的估计值及相关假设检验的结果。可见随机截距方差（即σ2μ0）的估计值为0.5988，标准误为0.2686。但此处未给出随机截距方差是否为0的假设检验结果。故没有客观依据判定σ2μ0与0 之间的差异是否有统计学意义。

以上是固定效应的解。因为此过程步运行的是空模型，所以这里只有一个固定效应，即截距，其值为-0.3018，表示y=0的总平均logit值为-0.3018。

以下是模型拟合的有关信息，包括三种信息标准的估计值和-2 倍的对数似然值。这些统计量本身不能说明模型拟合的优劣，但可用于含相同自变量数目的不同模型的比较。

以上是模型中参数的估计结果，包括固定效应和随机效应的参数估计值及相应的假设检验结果。注意，随机效应假设检验给出的是双侧检验的结果，而实际上检验方差是否为0应采用单侧检验，故此处所得的P 值应除以2 才是正确的P 值，后同。“v_u0”对应的P值为0.0399∕2＜0.05，说明σ2μ0与0之间差异有统计学意义，分析时应采用多水平logistic回归模型分析。

以上是ICC的计算结果，其值为0.1487，对应的P值为0.0187＜0.05，说明数据存在一定的组内同质性，需采用多水平logistic模型分析该资料。

以下是第三个过程步的输出结果，即调用GLIMMIX 过程运行含解释变量drug的随机截距模型的结果，其截距项设定为0。可见，σ2μ0值为0.5984，解释变量系数为-0.4343。

以下是第四个过程步的输出结果，即调用NLMIXED 过程运行含解释变量drug 的随机截距模型的结果，其截距项设定为0。可见，解释变量 系 数 为-0.4409（P=0.0057＜0.05），σ2μ0值 为0.6221（P=0.0390＜0.05），二者与0 的差异均有统计学意义。另外，由“Fit Statistics”部分结果可知，-2 倍对数似然值为1225.1，略大于第四步构造的模型；但由“Parameter Estimates”部分结果可知，模型中共包含两个参数，参数个数较之前少了一个，且两个模型的拟合效果并无统计学差异（χ2=1225.1-1224.9=0.2，P＞0.05）。所以，使用此模型更合适。

解释变量drug的系数为-0.4409，且与0的差异有统计学意义（P=0.0057），说明试验药组与对照药组的疗效之差具有统计学意义。因exp（-0.4409）=0.6435，所以对照药组治疗成功率是试验药组治疗成功率的0.6435 倍。随机截距的方差“v_u0”估计值为0.6221，与0的差异有统计学意义（P=0.0390∕2＜0.05），说明水平1截距跨中心变异显著，即不同中心μ0j值存在差异。

5 讨 论

一般而言，响应变量为二值变量的高维列联表资料采用一般logistic 回归分析，但此法要求所有观测结局相互独立。对于研究个体存在聚集性特征时，应采用多水平模型。这样可将传统模型中的随机误差分解到数据层级结构相应的水平上，使得个体的随机误差更纯［5］。

采用PROC GLIMMIX 和PROC NLMIXED 过程来构建模型：首先建立不包含任何解释变量的空模型，以计算ICC值。若存在组内相关，则构建截距项不为0 的模型。若经检验得到此截距项与0 的差异没有统计学意义，则构建截距项为0的模型。