含分层复合材料层合板的接触阻尼特性

何 意， 肖 毅， 苏众庆

(1. 同济大学 航空航天与力学学院，上海 200092；2.香港理工大学 机械工程系，香港 999077)

先进复合材料正逐步取代传统的金属材料作为新一代结构材料被广泛应用。然而复合材料构件在全服役周期中，由于各种载荷的作用不可避免地会产生各种缺陷，而分层损伤是其主要失效形式之一，由其引起的结构抗压、剪切强度的大幅下降将严重威胁结构安全。因此，对复合材料结构分层损伤进行早期诊断是一项具有重要工程价值的研究工作。

研究表明，当复合材料层合板中产生分层损伤时，其结构动态响应将会发生显著变化，而这些主要反映在模态参数的变化上，因此模态参数分析是分层损伤系统识别的重要手段[1]。一般模态参数主要包括振型、频率以及阻尼三个参数。早期研究主要关注如何建立动力学模型以准确计算分层板模态频率，试验及计算结果表明，在低阶模态下分层早中期阶段(分层比小于等于50%)频率改变不明显，仅表现出5%以内的偏差，对于分层早期诊断没有实质性作用[2-5]。对振型分析而言，大量试验以及数值分析表明，在分层早中期阶段，直至第6阶模态前，分层板与无损板的振型均无明显区别[6-8]。对比振型与频率，可发现阻尼在分层早期中具有更高的敏感性，十分适合作为分层诊断的模态参数。一些工作主要通过对比试验数据得到了层合板阻尼因分层而显著上升的定性分析结果，并且其中部分工作对于分层板低阶阻尼进行了理论求解，但仅仅关注材料阻尼的影响，这造成了低阶模态阻尼的预测结果基本上表现为定值规律，这与试验中出现的阻尼上升现象不吻合[9]。实际中，约束端摩擦损耗、空气阻尼等间接因素均可造成阻尼升高，但上述结果已排除了不良干扰，因此可认为损伤结构仍存在内部能量损耗机制，其中由内摩擦造成的接触阻尼被认为是主要原因。早先，一些学者在动力学分析中主要采用干摩擦模型，然而无论是经典的库伦摩擦或是其弹性变形均认为耗能仅发生滑动阶段，未考虑前滑移阶段耗能机理[10-13]。基于上述研究的局限性，许多学者认为需要考虑前滑移阶段的位移-力关系，提出了一种黏性库伦摩擦模型，认为前滑动阶段中系统受黏性力作用，但该模型放弃了弹性库伦摩擦中的摩擦刚度[14-17]。

考虑接触问题的分层板有限元建模可以通过多种方式实现，以获得精确的分层板动态响应。Luo等提出运用弹簧连接给分层上下接触面设定约束，计算结果表明，弹簧刚度大小对结构频率响应并无明显影响，且计算数值普遍高于试验值，某些情况下偏离严重，说明该方法因未释放接触面张开的约束而导致了结构整体刚度偏高。为了释放张开的约束，Ju等[18-20]将罚刚度法用于分层接触面有限元建模，计算结果验证了罚刚度法对于计算分层板频率响应的准确性，说明该方法能更准确反映分层接触性质，然而他们的研究中并未对如何合理选取罚刚度给出相应的解释，或仅仅使用有限元软件的默认值。

基于上述背景分析，本文旨在建立描述分层板动态层间接触阻尼行为的理论模型。首先，采用应变能法(Specific Damping Capacity, SDC)[21-22]对复合材料材料阻尼进行有限元求解。然后，针对接触阻尼，基于黏弹性静摩擦模型建立静-滑动摩擦一体化的能量损耗理论框架。利用有限元软件Abaqus建立分层板的3维动力学有限元模型，并给出了接触层模量与罚刚度之间的转换关系，从而确定罚刚度的输入方法，同时给出接触阻尼的有限元导入方法。最后，运用自由衰减试验测得分层板的一阶模态阻尼，并将试验阻尼和时域响应分别与理论阻尼和有限元模型时域响应作对比，验证理论与有限元模型的有效性。

1 分层层合板阻尼

1.1 材料阻尼

分层层合板的整体阻尼性能包括了材料阻尼和接触阻尼两部分，因此首先要确定复合材料阻尼的求解方法。目前利用有限元求解复合材料阻尼性能的方法主要有弹性-黏弹性对应原理(Elastic-Viscoelastic Correspondence Principle)[23]以及应变能法。本文采用应变能法计算材料阻尼。

应变能法主要思想为：结构总的比阻尼容量可以表征为每一个振动周期内的损耗能量除以总应变能

ψ=ΔU/U

(1)

式中：ΔU为一周期内的损耗能量；U为不含阻尼情况下结构最大的应变能。为求解U，首先需要求解无阻尼系统的运动方程

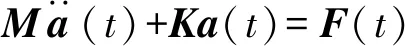
(2)

式中：M，K，F及a分别为结构的质量矩阵、刚度矩阵、载荷向量以及位移向量。由式(2)可求得系统应力向量σ、应变向量ε。根据弹性力学原理，应变能理论表达有

(3)

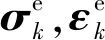
(4)

由式(3)和式(4)可得到材料比阻尼容量ψmat

ψmat=ΔUmat/U

(5)

有限元软件对式(3)和式(4)进行积分计算时，采用高斯积分法。该方法只需知道每个高斯积分点的积分点体积，以及对应的积分点处被积函数值，两者相乘即可得单个积分点积分值。事实上，Abaqus有限元软件计算后可直接导出模态下的积分点应力、应变及积分点体积值，运用以上数据即可计算应变能及耗散能。

1.2 接触阻尼

振动状态下，分层上下界面的接触被认为是导致阻尼上升的主要原因。为进一步理解分层界面能量耗散机制，提供定量分析分层界面接触阻尼方法，需建立相应的接触阻尼模型。

干摩擦一般用库伦摩擦模型描述，表1给出了该模型及其扩张形式。表中：FN为法向加载力；FT为切向加载力；fT为摩擦力；sc为黏滞阶段微滑移；μ为静摩擦因数，本文中均默认静摩擦因数与动摩擦因数一致。其中：“1”为经典库伦摩擦模型；“2”为考虑静摩擦弹性变形的弹性库伦模型；“3”为考虑静摩擦阶段为黏性变形的黏性库伦摩擦模型。库伦摩擦及其变形表现了摩擦理论对于前滑移阶段位移-摩擦力关系的发展。接触问题中，既存在滑动摩擦也存在静摩擦，同时接触界面还存在着一定的接触刚度，因此需要将上述模型进行结合。该模型同时需要描述滑移阶段和前滑移阶段的能量损耗，还需要考虑到实际存在的接触刚度影响，据此需要建立静-动摩擦一体化能量损耗模型。

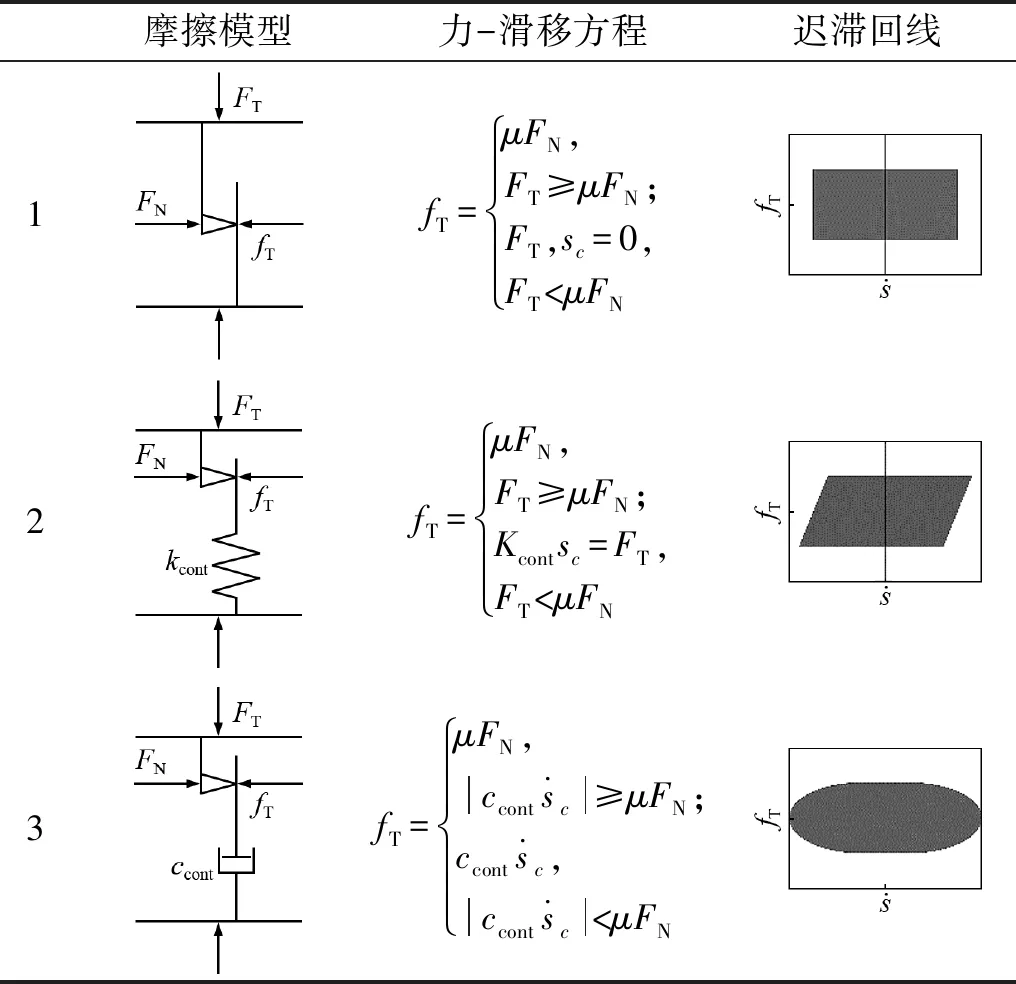
表1 不同干摩擦模型及其方程表达与迟滞回线

对于黏滞阶段，考虑上下接触对之间的静摩擦，为同时引入接触刚度以及黏性耗能，将其描述为Kelvin黏弹性模型

(6)

式中：τcont,γfric为由静摩擦造成的界面切向应力与切向应变；Gcont为静摩擦等效切向接触模量；ccont为静摩擦等效切向黏性阻尼系数；若此处忽略界面粗糙度影响可认为Gcont与ccont为接触面树脂材料的剪切模量与黏性系数，Gcont=891.30 MPa，ccont=Gcont(2ξcont/ωr)(ξcont为树脂材料阻尼比，约为0.008)。设第r阶模态下，sc随时间变化有(默认初始位置为0，相位为0)

sc=sasin(ωrt)

(7)

式中：sa为单点静摩擦接触循环周期内最大微滑移距离。设h表示接触的变形厚度，则γfric可表示为

(8)

将式(8)代入式(6)

(9)

式(9)中h对于实际的粗糙材料可由显微镜观察得到，虽然忽略了粗糙度影响，但为与实际接近，取文献[24]中h值0.005 mm。ωr为第r阶模态频率;将式(9)转换为二次曲线形式，则有

(10)

该二次曲线为一倾斜的椭圆迟滞回线(见图1)。其包围面积即代表损耗能量，则单点接触一周期内的损耗能量有

(11)

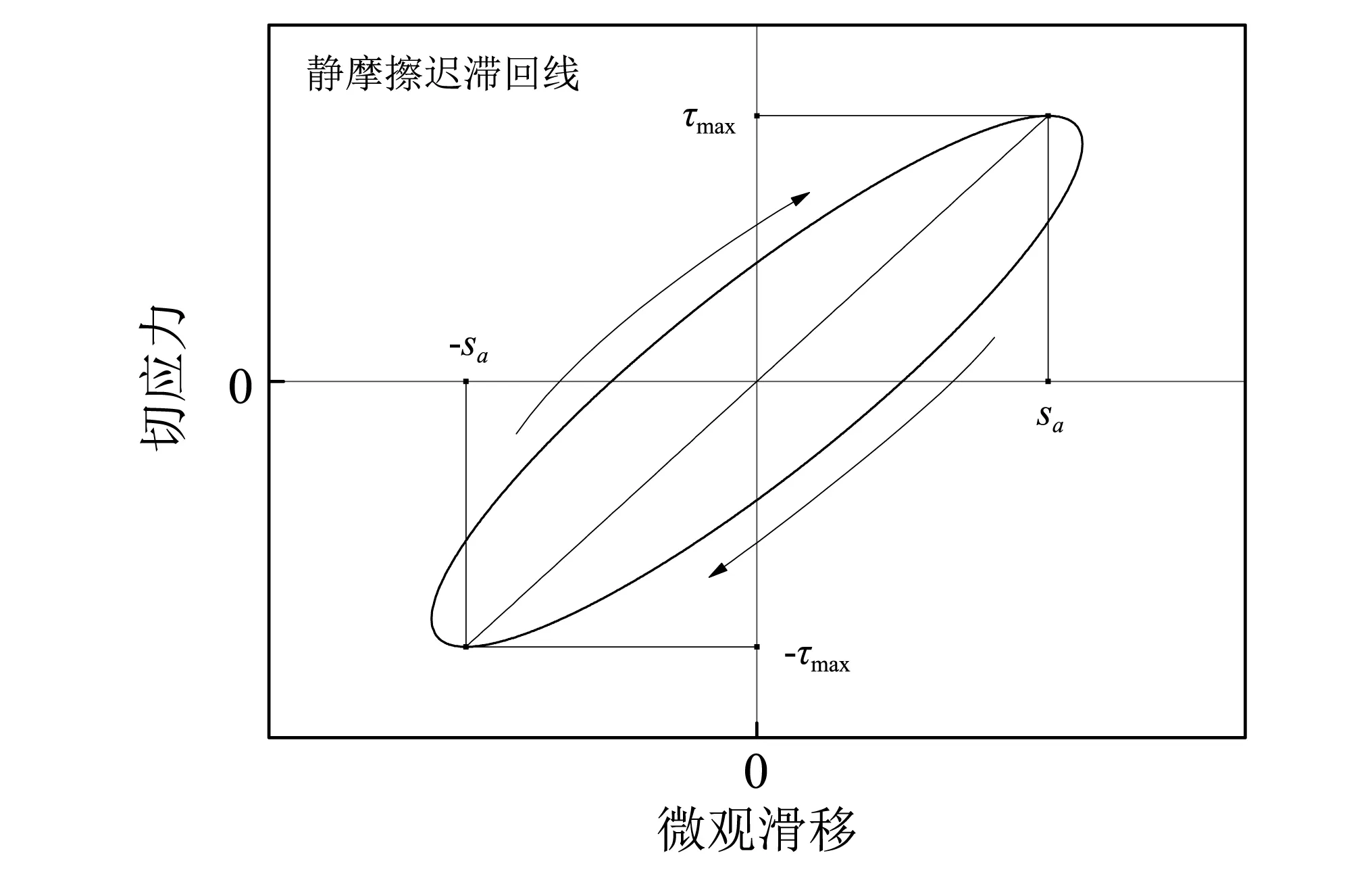
图1 Kelvin黏弹性静摩擦迟滞回线Fig.1 Hysteresis loop of Kelvin viscoelastic static friction

当FT超过最大静摩擦力摩擦阶段中出现滑动摩擦，此时迟滞回线无法维持完整的椭圆，迟滞回线会出现削平顶部的情况，削平起始点即为椭圆迟滞回线中应力最大点，其对应的sc为

(12)

式(12)中存在ccontωr≪Gcont，易知应力最大点约等于sa，该性质反映了由于椭圆函数的特性，使得应力最大点与微滑移最大点并不重合。图1已做夸大处理，实际中应力最大点与微滑移最大点十分接近，为简便计算在后文中默认两点重合。产生削平效应后，原迟滞回线拓展出一平行四边形区域，新的迟滞回线为

(13)

式中:sb为滑动1/2摩擦滑移距离，该静-动摩擦一体化能量损耗模型可用图2表示。图3为该模型迟滞回线。

此时，损耗能量将需要加上滑动摩擦部分，单点接触一周期内的损耗能量为

(14)

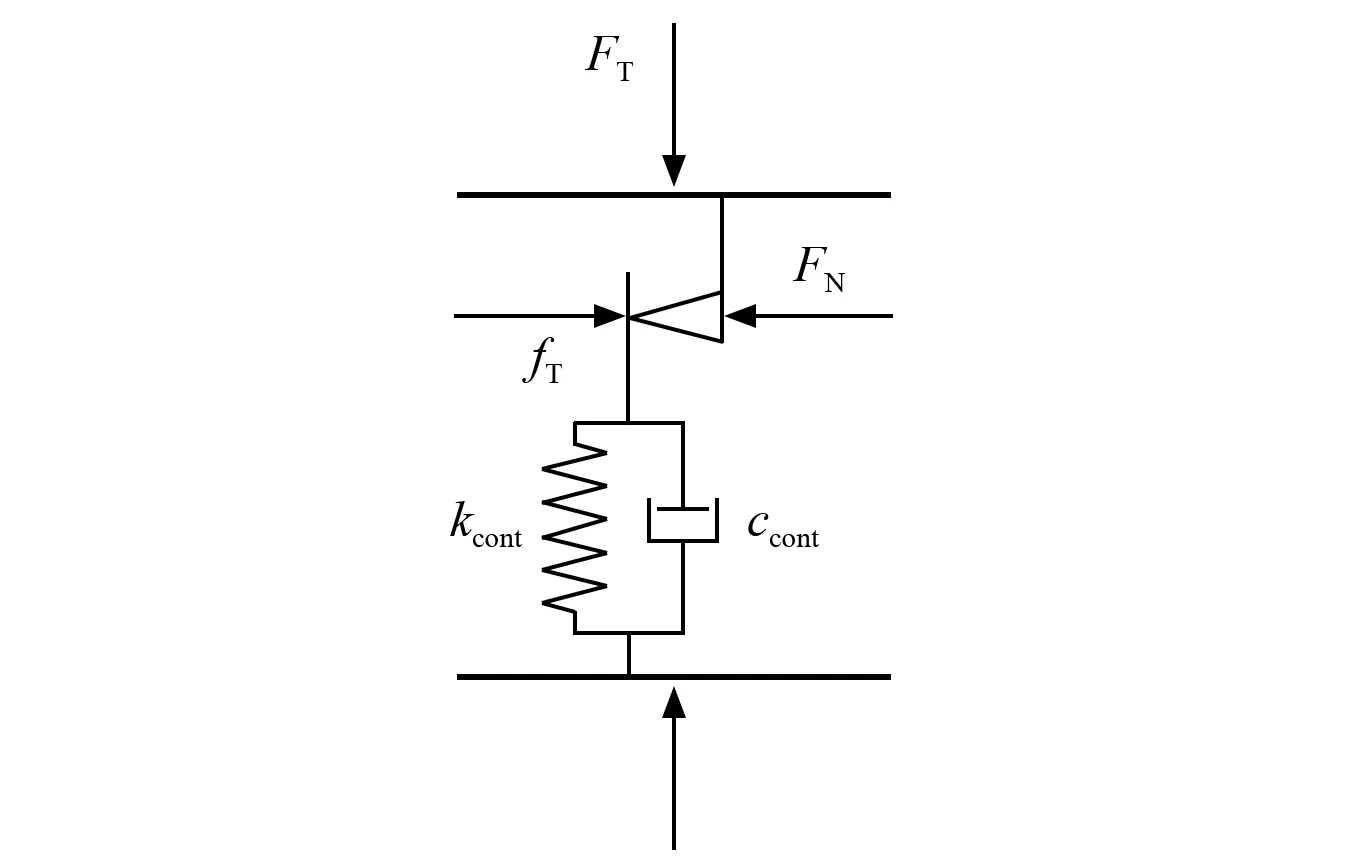
图2 静-动摩擦一体化能量损耗模型Fig.2 Static-slip-integrated friction energy-dissipated model

将式(14)在整个接触域进行积分，得到结构总接触损耗能量

(15)

类似应变能法，可同样得到接触比阻尼容量ψcont

ψcont=ΔUcont/U

(16)

式(5)与式(16)相加，即得到整体分层板结构的比阻尼容量

ψ=ψmat+ψcont

(17)

将比阻尼容量以阻尼比形式表示[25]

(18)

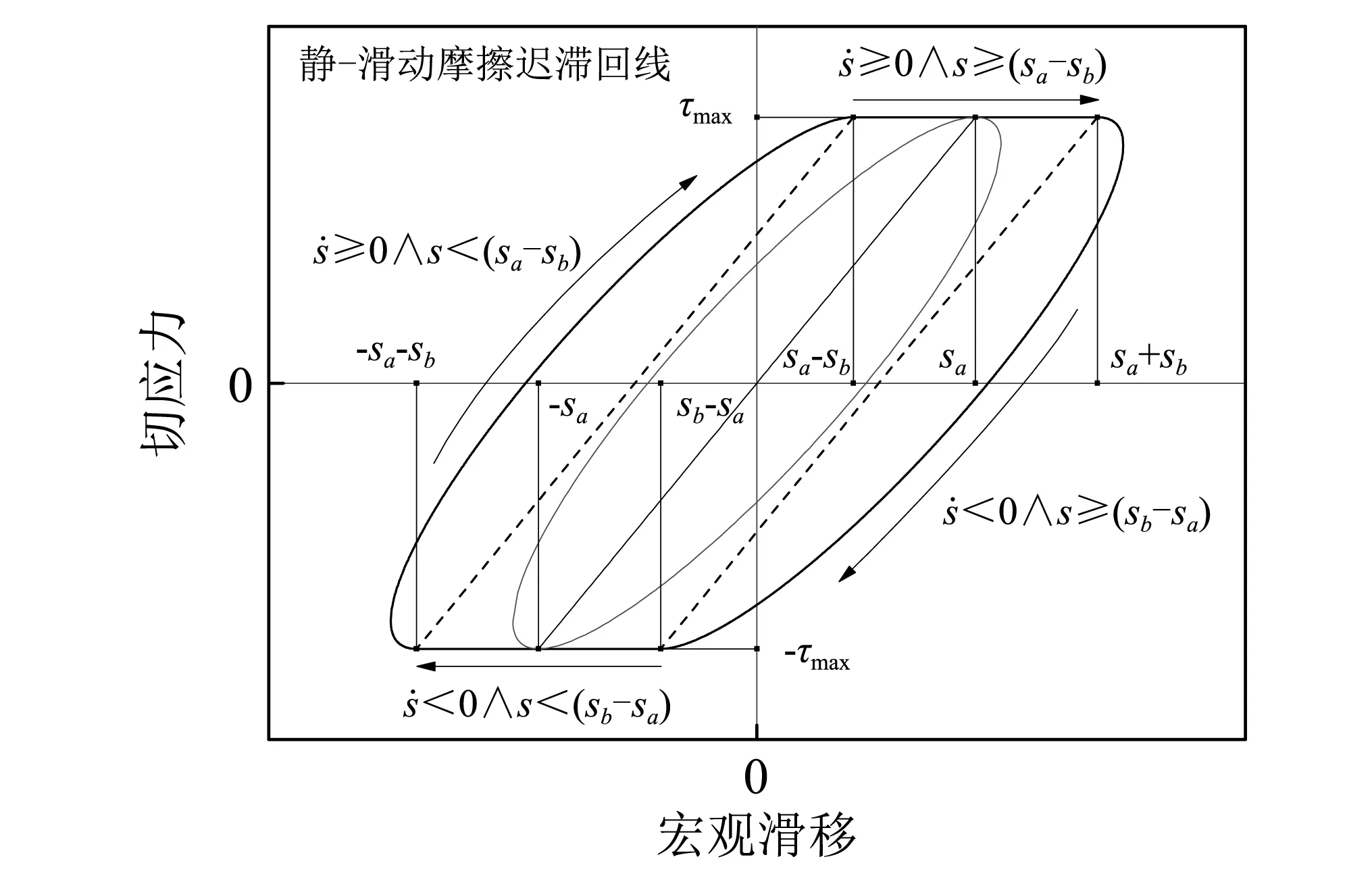
图3 静-动摩擦一体化能量损耗模型迟滞回线Fig.3 Hysteresis loop of static-slip-integrated friction energy-dissipated model

2 分层层合板有限元模型

2.1 分层界面接触对

接触问题的数值计算呈现出高度复杂的非线性现象，需要强大的求解器来避免收敛问题。因此，本研究使用通用有限元软件Abaqus来构建3D动态隐式模型，该软件具有用于接触建模的高级稳定控制。建立分层层合板有限元模型的关键在于运用合理的方法描述分层接触问题，它既能反映真实分层界面边界条件，又能提供良好收敛性能使其在尽可能短的时间提供足够精度的结果。Abaqus中提供了Interaction模块用以建立部件表面接触行为。

Abaqus建立接触主要有两种约束形成方案：节点到面的离散及面到面的离散。面到面的离散会为整个接触面(而不是单个节点)建立接触条件，可在分析中同时考虑主面和从面的形状变化，节点穿透的程度低于节点到面的离散，因此一般情况下，面到面的离散得到的接触应力结果精度要高于点对面离散。为避免过于严重的穿透以及得到更精确的接触应力，选用面到面离散方法。

对于主从面的选取，在接触对中，建议选择具有较高刚度的表面作为主表面，而较低刚度的表面作为从表面。对于偏置分层板，由于分层的上部比下部薄，因此为较低刚度表面，被定义为从面；相应地，下部表面被定义为主面。对于中央分层板，由于上下部刚度相同，主、从面选取不受限制，可保持与偏置分层板设置相同。分层界面在振动过程中，由于上下节点对之间不存在切向的错位迁移，则滑动方程可选择小滑移模式：该模式默认节点不存在切向错位迁移，接触行为只发生在起始时的各节点对之间，计算过程无需判断节点迁移，可提高计算效率。

设定约束形成方案后需定义接触属性。对于法向，应给定压力-过盈关系以模拟界面间不可穿透约束。压力-过盈关系主要有硬接触和软接触两种。硬接触条件可以最小化从主表面间的穿透，且对于隐式算法软接触计算时间成本更高，因此选用硬接触，其压力p与过盈关系hover有(见图4)

(19)

硬接触中Abaqus提供了三种不同的实行方法：直接法、罚刚度法、增广拉格朗日法。综合收敛性以及精度要求，选取罚刚度法。罚刚度法中，压力是过盈量的函数，两者关系分为线性与非线性两种，此处选用线性关系

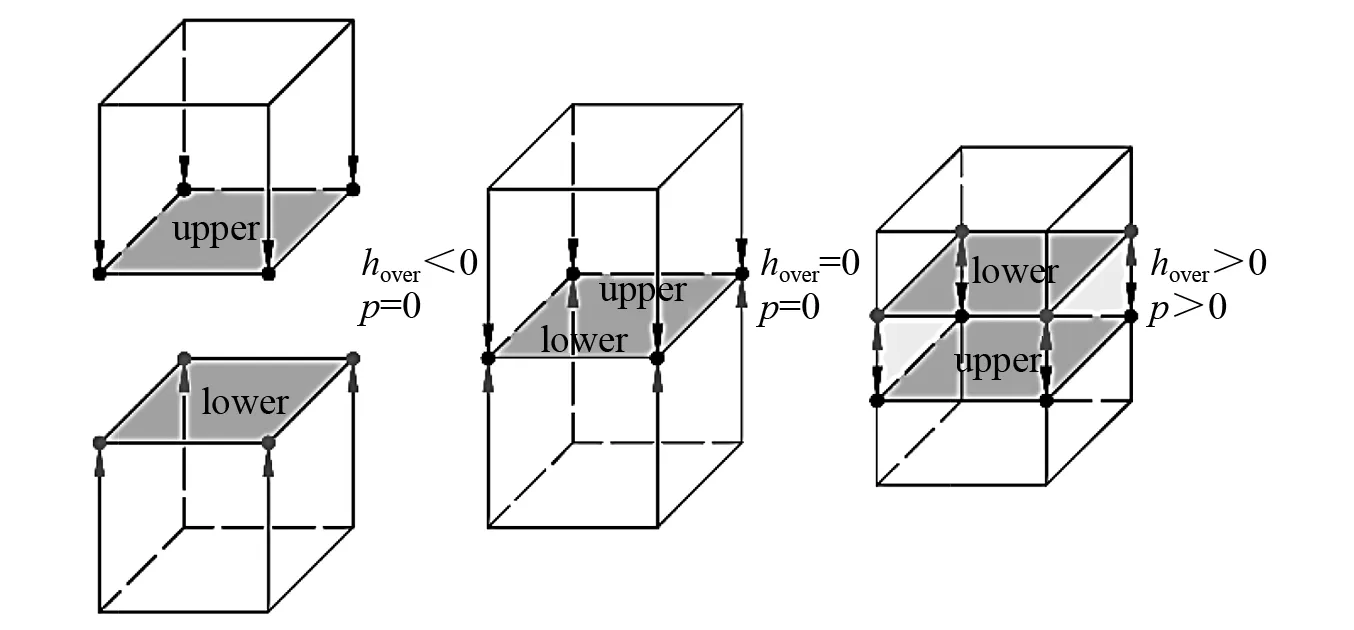
图4 压力-过盈关系Fig.4 Pressure-overclosure relationship

p=Khover

(20)

式中：K为罚刚度，MPa/mm。

最后，需在接触属性中引入阻尼。在有限元接触模型中引入接触阻尼是一个难点。将接触层虚拟为一层含阻尼的薄层材料是其中一种方法[26]。该方法实际将接触上下表面固结在一起，无法实现动态下接触界面的张合，对于分层等张合明显的弱接触行为，会对结构模态结果产生较明显的影响。本次有限元建模中，采用接触属性中阻尼(Contact Property—>Damping)选项引入接触阻尼。该选项阻尼定义为抵制接触面之间的相对运动，阻尼系数是间隙距离的函数，有线性与分段线性两种函数关系，为简易定义与计算稳定，取线性关系。

2.2 罚函数接触刚度

罚函数法是约束变分原理中的一种，利用约束变分原理得到修正泛函，其解近似地满足接触面的不可穿透性条件。因此，式(20)中的罚刚度K数学意义为约束变分原理中约束缩放因子，K越大约束条件满足越好，模型越逼真，但过大的K将导致收敛性下降。

由上述可知，原则上值的意义仅存在于数学层面，无明确的物理意义。然而在式(8)中，模型假设了接触面的变形发生在厚度为h的接触层以内，其接触层法向受压时存在变形，该假设与K值的数学意义相似，即类比过盈量为接触层变形量(见图5)。因此，根据接触层的弹性模量可得到K的大小。

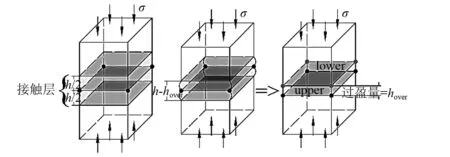
图5 接触层变形等效节点过盈Fig.5 Equivalent node overclosure quoted from deformation of contact layer

注意到，K单位为MPa/mm，而接触层弹性模量Econt单位为MPa，因此二者转换实质为量纲转换。有限元单元本构关系有

σe=QBae

(21)

式中：ae为单元位移向量；Q为本构矩阵;B为应变矩阵。其中QB可表示为

S=QB

(22)

式中：S为应力矩阵，其展开得到

S=[QB1…QB8]=[S1…S8]

(23)

式中：Si,33项为单元ζ方向(接触面法向)的应力矩阵分量

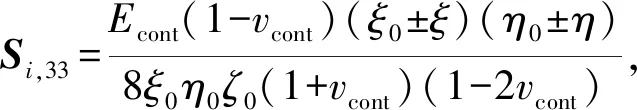
(24)

正负号对应节点在单元局部坐标中的坐标正负号。式(24)中并不包含ζ方向的自变量，因此Si,33对于该方向是常量。设单个单元在板厚变形量为Δh，则厚度方向应力为

(25)

此时得到一个厚度方向位移与压力之间的本构关系，令K等于该本构

(26)

式(26)表现了K从数学含义向物理含义的传递。

2.3 接触阻尼引入

接触属性中的阻尼系数定义为

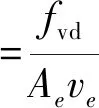
(27)

式中:Ae为节点面积；ve为接触节点对相对运动速度；fvd为阻尼力大小，易知该阻尼系数单位为MPa·s/mm。事实上式(27)表示了Abaqus中的接触阻尼是等效黏性阻尼，该系数被定义为法方向阻尼系数，为考虑切向阻尼，还提供了切向系数，默认的切向系数为0。本文中主要考虑切向的阻尼效应，为突出切向的影响，此处取较大的切向系数1 000。

对于线性阻尼系数-间隙函数，需定义间隙距离，该参量意义为：若接触节点对之间的距离在所定义的间隙内，则考虑阻尼效应，否则不考虑。经试算发现，当间隙距离较小时，计算结果稳定性下降，当间隙距离大于分层面在振动下的最大分离距离时，稳定性良好。此时，所有接触点对在完整振动周期内均受阻尼力影响，第k接触点对单周期内损耗能有

(28)

整个接触面总损耗能为

(29)

在激励相同情况下，式(29)中除ϑ外均是常数，总应变能U与式(5)相同情况下阻尼比为

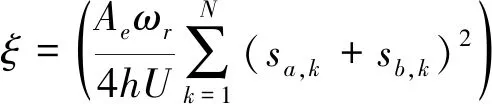
(30)

式(30)的括号表示一个常数，显然该阻尼选项中阻尼系数与最终求得的接触阻尼比呈正比例关系。由“1.2”节所述的接触阻尼比已知，根据式(30)容易求得对应的输入阻尼系数ϑ。为验证式(30)，取不同的ϑ代入并计算模型在该接触阻尼系数下的阻尼比，其结果如图6所示。

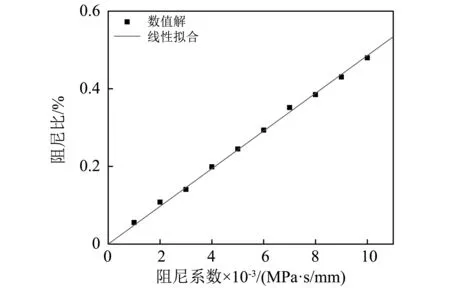
图6 有限元接触阻尼系数与结构整体阻尼比之间的关系Fig.6 Relationship between the contact damping coefficient in FEM and the integrated damping ratio of the structure

2.4 基于有限元模型的求解流程

从式(4)与式(16)可知，欲求得分层板材料阻尼与接触阻尼，需要知道应力、应变、积分点体积、接触应力与接触滑移距离等信息，本文理论计算均需与有限元模型结合。传统的Frequency以及Modal dynamic等线性摄动步对于含有接触非线性(约束变分)的模型不能求解，运用Dynamic Implicit可有效模拟含有接触非线性模型的动态响应。Dynamic Implicit采用直接积分方法对总体矩阵方程进行求解，相比Modal dynamic计算时间更长，但能良好反映接触状态以及接触对整体结构响应的影响。图7给出了具体求解流程，主要步骤如下：

步骤1运用Dynamic Implicit分析步计算无阻尼系统的一阶动态响应；

步骤2从步骤1中输出应力、应变、积分点体积、分层接触面接触应力以及滑移距离；

步骤3提取应力、应变以及积分点体积数据，结合复合材料各方向阻尼比分量运用应变能法求解一阶模态材料阻尼；

步骤4提取接触应力以及滑移距离数据，运用静-滑动摩擦一体化接触阻尼模型计算一阶模态接触阻尼；

步骤5将计算得到的材料阻尼与接触阻尼导入原阻尼结构，并计算有阻尼系统的一阶动态响应。

3 动态参数测试

采用自由衰减法进行一阶模态阻尼试验，该方法操作简便且数据精确。测试步骤为：给结构一个瞬时激励后，得到一阶模态下结构的自由衰减曲线，通过拟合时域数据中的各波峰值得到衰减函数曲线，从而到阻尼比参数。

对于欠阻尼系统(ζ<1)某点的位移有如下形式通解

(31)

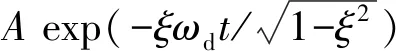
复合材料的一阶模态材料阻尼随着一阶模态频率上升而上升，其大致满足经验公式[27]

ξ1st-order=aln(f1st-order)+b

(32)

式中：a和b为需要通过试验确定的系数。

试验中不可避免存在空气阻尼影响，一定振幅下阻尼和振幅成线性关系，可通过线性拟合法排除空气阻尼干扰[27]。

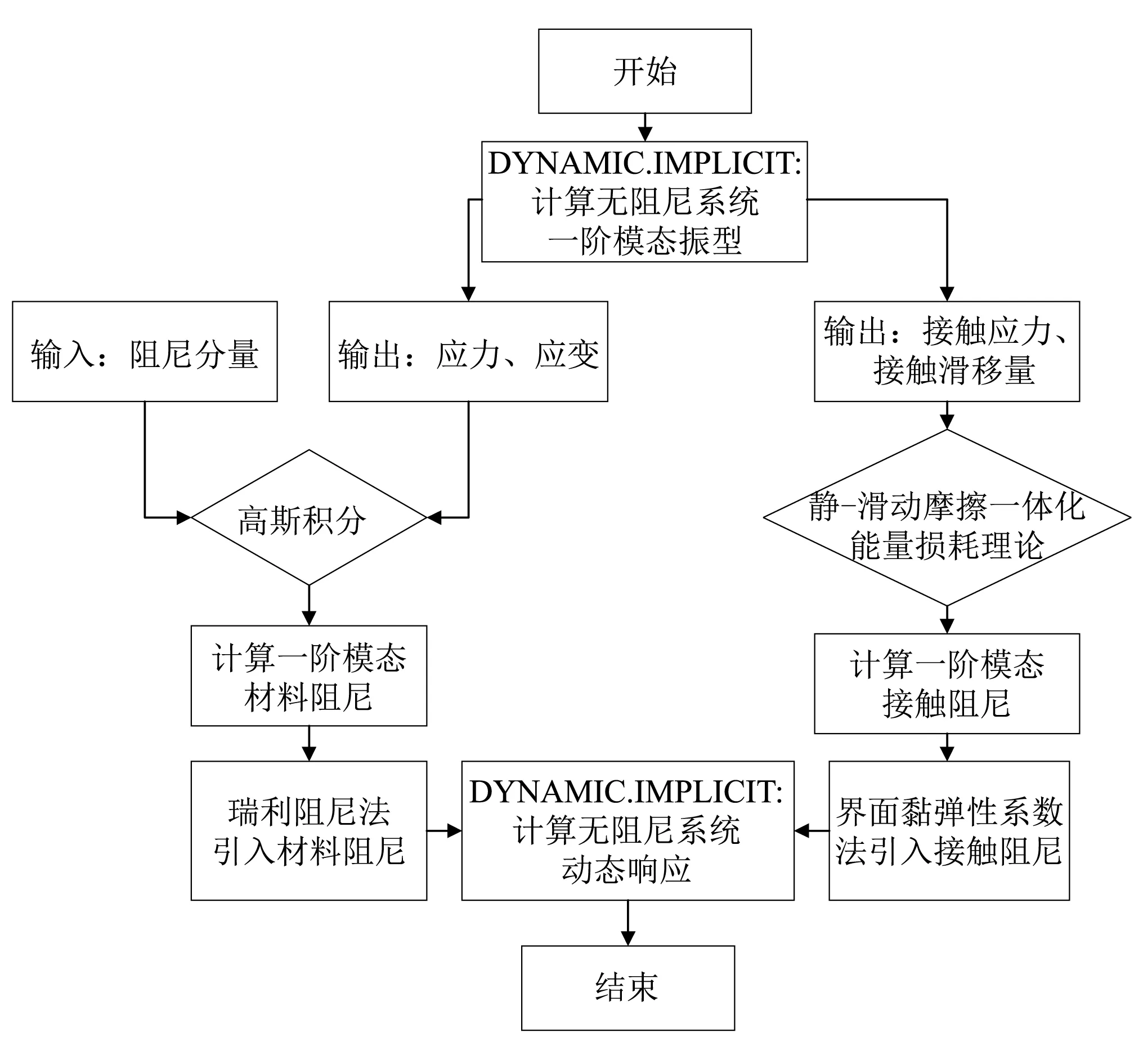
图7 结合有限元模型的求解流程Fig.7 Solving process combined with FEM

本试验用材为威海光威复材公司提供的碳纤维/环氧(T300/7901)预浸料，层合板铺层为正交铺层[0/902/02/902/0]s，材料参数见表2。板件制备中，以聚四氟乙烯薄膜作为预埋分层材料埋入铺层特定位置，薄膜厚度为0.025 mm。工程中，包括冲击、边缘应力以及生产缺陷等工况主要造成宏观分层，且振动主要也局限于对宏观分层的探测。为符合工程中的损伤容限需求，设置分层长度为40 mm，取五组不同全长试样(分层比例)：90 mm(44.4%),130 mm(30.8%),170 mm(23.5%),210 mm(19.0%)和250 mm(16.0%)，主要讨论早期宏观裂纹，不设置大于50%分层比例的试样。试样尺寸及分层厚度方向位置见图9，“//”代表分层。图10为试样实物图。

表2 T300/7901碳纤维/环氧树脂复合材料力学参数

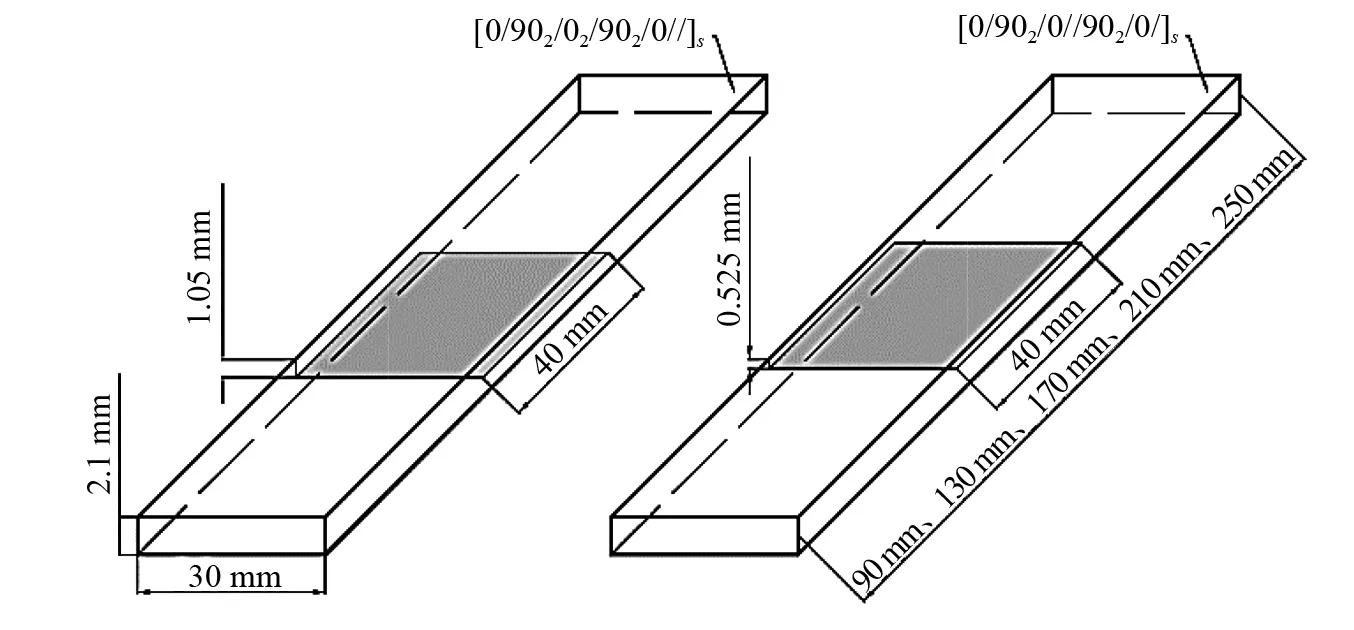
图9 预埋分层试件几何尺寸Fig.9 Geometry of delamination-preset composite plate specimens

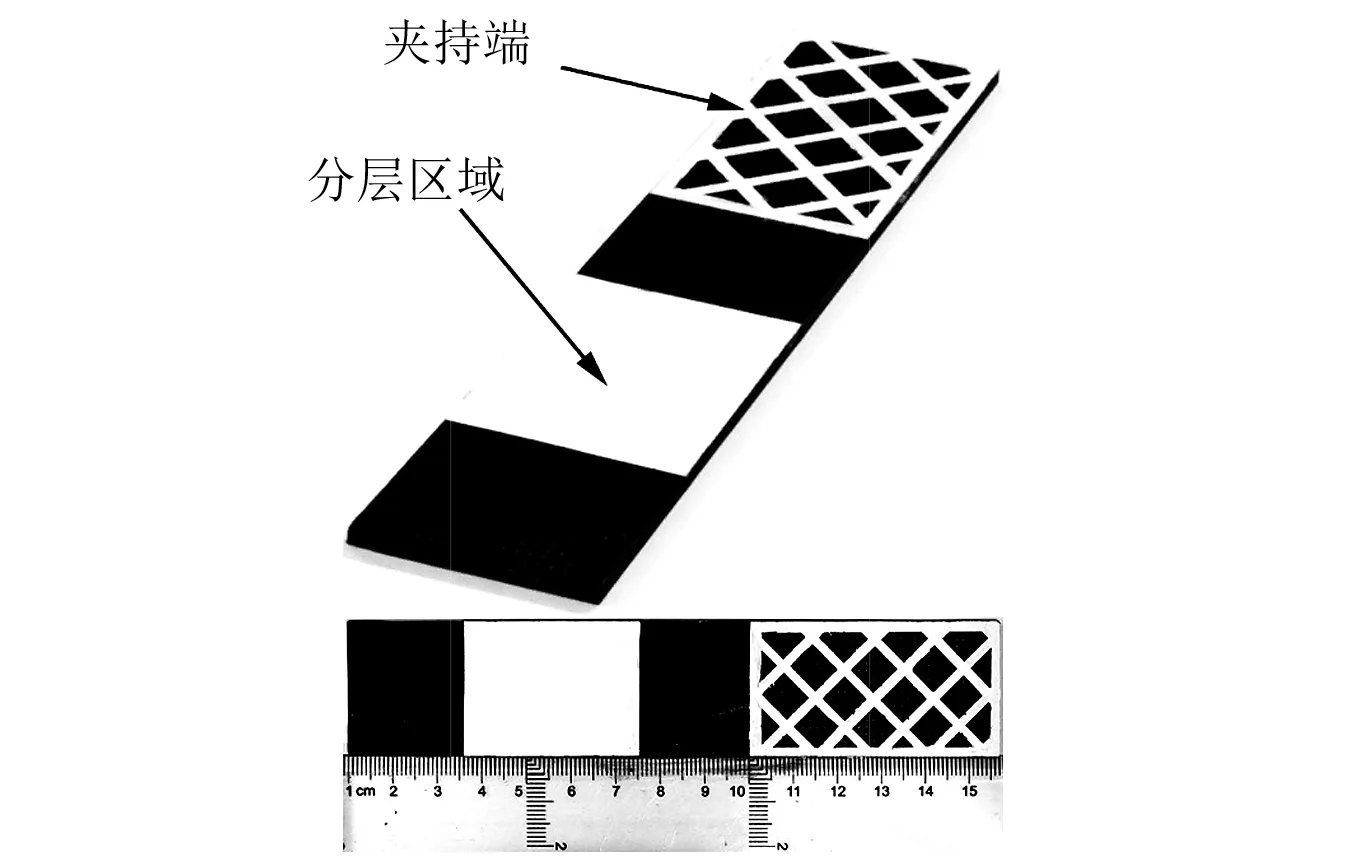
图10 预埋分层试件实物Fig.10 Delamination-preset composite plate specimens

4 结 果

由前述可知，为了计算材料阻尼以及接触阻尼，需先对无阻尼板进行有限元计算。分层板存在稳定的模态接触阻尼前提是其在该模态下存在稳定的接触状态，为此首先需讨论不同模态下的接触状态。通过“2.2”节方法求得罚刚度并导入有限元模型，计算其前三阶接触状态，计算结果见表3。

表3表现了44.4%偏置分层板前三阶模态在半个周期(波峰至波谷)内的五个相位点接触情况，显然前三阶模态的接触状态各有不同：一阶模态接触基本发生在分层两端界处；二阶模态则集中于两端界对角点处；三阶模态集中在分层中部处。前两阶模态接触在0相位处发生突变，分别由原接触端界/对角点转移到另一端部，而三阶模态接触则表现为由闭合到张开的呼吸效应。上述结果表明当分层板处于某一模态时，其具有稳定的接触状态，这一特性保证了分层板能有稳定的模态接触阻尼。

表3 44.4%偏置分层板有限元模型前三阶模态接触状态

对于分层板的两部分阻尼，首先需准确得到复合材料的材料阻尼，其关键在于准确得到复合材料各个方向阻尼比分量值。一阶阻尼比各分量与一阶频率有关，需通过试验得到阻尼比分量与频率的函数，通过裁切不同长度的板件得到不同一阶频率的数据；对于不同分量，通过测试不同纤维方向无损单向板得到，即分别测试0°，90°以及45°单向板以得到ξ11,ξ22(ξ33)以及ξ12(ξ13)，ξ23采用经验方法表示为ξ23=ξ12/2，图11(a)、图11(b)和图11(c)分别表现了0°，90°以及45°无损板的测试结果及拟合曲线，所得阻尼比频率依赖性表达式见表4。

为了验证拟合公式，将所得公式用于SDC法计算“3”节所述铺层的无损层合板阻尼，并与试验值对比(见图12)。结果显示，试验值拟合的公式与计算值拟合的公式相比接近，在低频部分吻合良好，在高频部分误差稍大，从图12可知，在60～80 Hz的试验阻尼比飙升源自于该频域段为夹持机械的共振频率。通过对比可知，所得阻尼比频率依赖性表达式满足对分层板材料阻尼计算的要求。

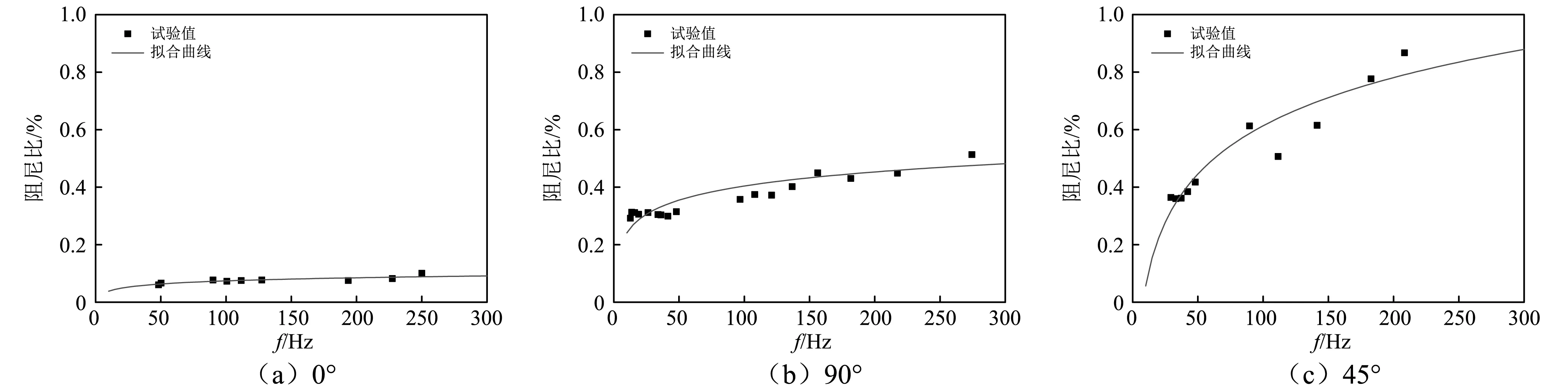
图11 单向板一阶模态阻尼试验值及拟合结果Fig.11 Experiment and fitting 1st-order damping ratio results of unidirectional composite plates

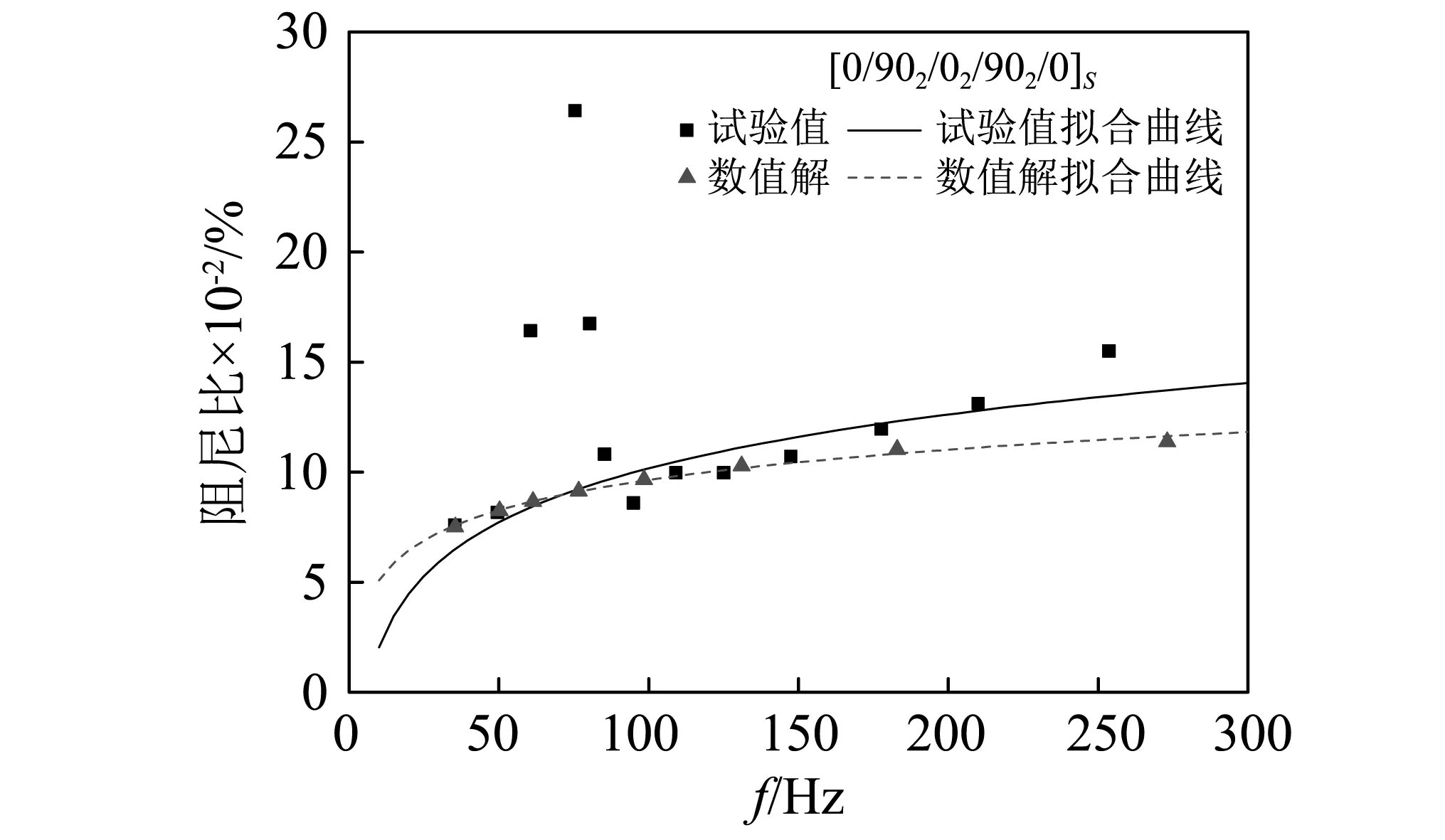
图12 正交层合板一阶模态阻尼试验值及拟合结果Fig.12 Experiment and fitting 1st-order damping ratio results of cross laminated composite plates

将接触应力与滑移距离信息运用到静-动摩擦一体化能量损耗模型，计算分层板一阶接触阻尼，并与此前应变能法得到的材料阻尼相加得到分层板一阶模态阻尼。图13给出了两种分层情况的分层板一阶模态阻尼试验以及理论计算结果。从图13可知，当层合板含有分层时一阶模态阻尼将明显地上升，且两种不同分层位置的分层板一阶模态阻尼均随分层比例上升而上升，此外中央分层板阻尼普遍高于偏置分层板阻尼。显然，阻尼对于早中期板件的分层损伤具有较高的敏感度，是一项适合用于分层检测的模态参数。此外，图中给出了理论计算的接触阻尼(虚线)，接触阻尼随分层比例上升的趋势十分明显。总体上，理论计算结果与试验值反映出相同的阻尼变化趋势，其中偏置分层组理论与试验吻合良好，而中央分层组除分层比44.4%一项外，其余各项数据基本也处于较小的误差范围内。

表4 T300/7901碳纤维/环氧树脂复合材料阻尼分量

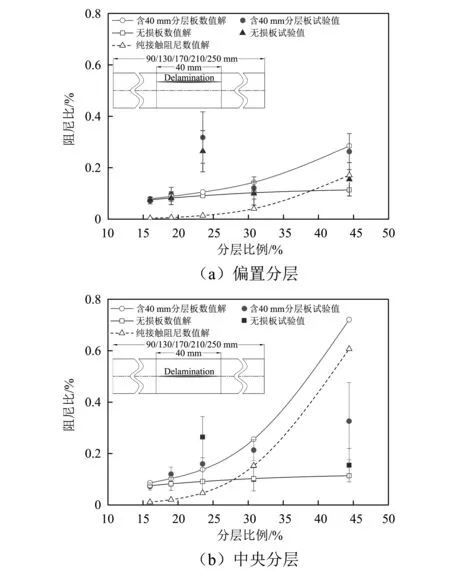
图13 分层板一阶模态阻尼试验值与理论值Fig.13 Experiment and fitting 1st-order damping ratio results of delaminated composite plates

将上述理论结果导入有限元建模，并计算有阻尼情况下的动态响应。其中材料阻尼以瑞利阻尼引入，接触阻尼由“2.3”节所介绍的方式引入。分别选取偏置、中央分层两组试件中分层比例为19.0%，30.8%和44.4%项进行有限元模拟，模拟结果与试验结果如图14所示。图中的试验结果经过滤波处理，仅保留了一阶的自由衰减。首先，从图14的波形图可知，有限元模型的一阶模态频率，对比试验频率值，两者基本一致，表明该种建模方法有效反映了裂纹引起的结构刚度退化。其次，衰减曲线同样表现出与试验接近的衰减规律，接触阻尼对整体结构响应的影响通过上述接触阻尼引入方法得以表现。图13(b)所表现的中央分层组分层比44.4%一项理论值与试验值相差较大的情况在图14 (d)也有相似反映。

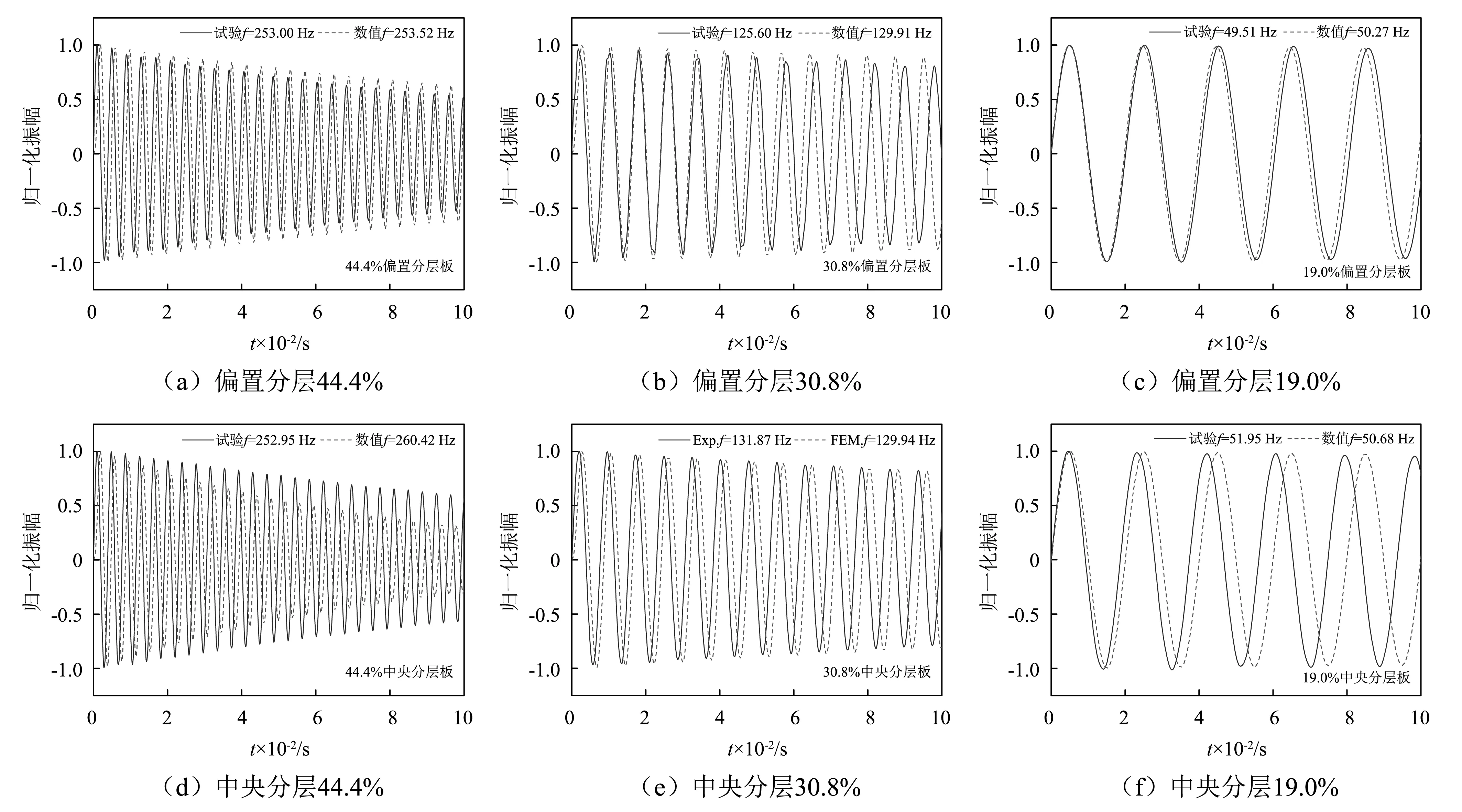
图14 考虑接触阻尼有限元模型时域响应与试验时域响应Fig.14 The 1st-ordertime-domain responses of experiment and FEM models with contact damping setting

最后，为表现现实中分层板在振动过程中的“呼吸效应”，选取分层比为44.4%偏置分层一项进行稳态振动仿真，激励频率为第三阶模态频率，该项的分层在第三阶模态下具有较为明显的张合现象。图15表现了该有限元模型第三阶模态-π/2相位模态振型。图16表现了该有限元模型分层上下接触面某对应点的时域响应。明显地，该有限元模型有效地模拟了上下接触面的相互作用，并由此引起了振动过程中的“呼吸效应”。

图15 44.4%偏置分层板有限元模型第三阶模态-π/2相位模态振型Fig.15 The -π/2 phase 3rd-order modal shape of the 44.4% offset delaminated composite FEM model

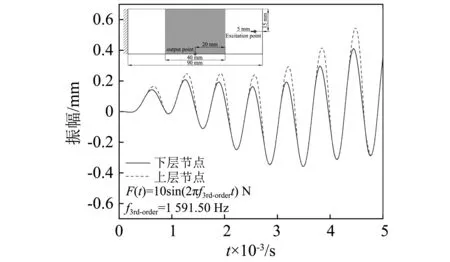
图16 44.4%偏置分层板有限元模型分层上下接触面某对应点的时域响应Fig.16 The time-domain response of a certain node-pair on the 44.4% offset delaminated composite FEM model

5 结 论

本文从理论、试验以及有限元模拟三个方面对分层层合板一阶模态阻尼特性进行了详细的研究。首先，运用应变能法求解了复合材料材料阻尼，同时基于静-滑动摩擦一体化方法建立了求解分层界面接触阻尼的理论模型。然后，运用有限元软件Abaqus建立了求解分层层合板动态响应的三维有限元模型，并确定了罚刚度与接触层模量的定量关系，同时给出接触阻尼导入有限元模型的方法。最后，运用自由衰减法进行了试验研究，验证了模型的有效性，主要结论如下：

(1) 罚刚度法能有效模拟分层接触面间的接触状态，且罚刚度取值与实际接触层模量间具有特定关系；

(2) 分层会显著提高复合材料层合板的阻尼性能，试验与理论计算结果均表明：分层比例越大，层合板一阶模态阻尼上升越多，其中接触阻尼起主要作用。

(3) 在厚度方向上，中央分层板模态接触阻尼普遍高于偏置分层板。

(4) 静-滑动摩擦一体化模型能有效求解分层板一阶模态接触阻尼，该方法有效印证了接触阻尼的主要来源为分层界面间摩擦所导致的能量损耗。