构造基本不等式模型，探求函数最值求解技法*

江苏省西亭高级中学 (226300) 瞿春波江苏省南通市通州区教师发展中心 (226300) 瞿国华

利用基本不等式(以下简称为“公式”)求函数最值时，变形是基础，恰到好处的变形是关键.本文就如何构造“公式”模型，谈谈笔者的一些想法，不当之处，敬请批评指正.

1.转化符号

若含变量的项是负数，则提取负号，将其转化为正数[1]，再利用“公式”求最值．

2.配凑定值

将目标函数恒等变形或适当放缩，配凑出两个式子的和或积为定值.

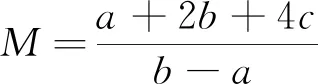
3.验证等号

使用“公式”时，必须检验等号能否成立，否则无法求得最值；若是多次使用“公式”时，则要注意多个取等条件是否同时成立．

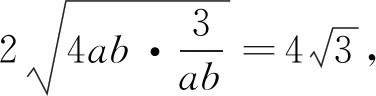
4.常量代换

若已知条件中的“1”(常量可化为“1”)与目标函数之间具有某种关系(尤其是整式与分式相乘模型)，则实施“1”代换，配凑和或积为常数.

例4 (2019南京高三期末)若正实数a,b,c满足ab=a+2b,abc=a+2b+c，则c的最大值为．

5.代入消元

对已知条件作适当变形，将某个变量用其余的变量线性表示，代入目标函数，构造和或积为定值，从而求得最值.

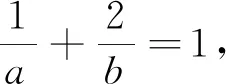
6.整体换元

通过设置主动临时横撑可以有效减小由于采用塔梁异步施工工艺引起的塔柱根部拉应力，确保塔柱施工质量，从而实现安全、质量、进度兼顾。该工艺在九江长江公路大桥的成功实施，拓展了索塔横梁的施工方法，具有较高的推广价值。

若已知(或待求)因式之间具有某种关系，则引入一个或几个新的变量，替换掉原先某些因式，构造和或积为常数.常见的换元方法有比(倍)值换元、差值(增量)换元[2]、单换元、双换元等.

7.转化为不等式

若已知“和与积”的等式关系，求“和与积”的最值，则利用“公式”转化为解不等式.

8.乘方

若目标函数带有根号，则先乘方后配凑为和为定值[1]．

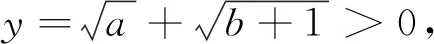
9.拆(添)项

将已知条件中某些项拆(添)成多项之和或多个因式之积，使得它们的和或积为常数[1]．

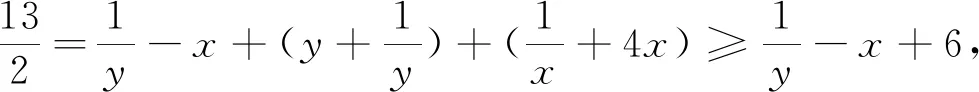
10.引入参数[1]

若对系数配凑难以下手时，则引入参数，利用待定系数法建立系数之间的比列关系或微调至“各数”相等.

11.齐次化

将目标式变形为齐次分式(分子分母各项次数相同)，通过换元或分离等手段得到和或积为定值.

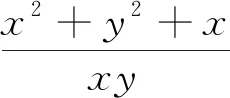
12.确定主次元

若多元问题中变量较多时，则优先确定主次元，然后消去次元，从而转化为主元条件下利用“公式”求解目标函数最值.

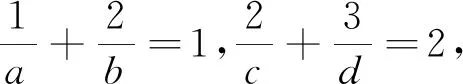
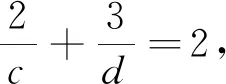
总之，当遇到无法直接使用“公式”求最值时，可以通过构造、变形，转化为“公式”模型.解题时，不应局限于某一种“变换”，应多种技法交互，多样思维融合，这就需要我们因题而异，灵活变通，深挖题目的隐含条件、细心观察目标函数的结构特征[2]，从而找到最优解法.