核心素养视角下的高三解题教学研究——以2019年浙江数学高考卷第16题为例

江苏省灌南高级中学 (222500) 刘鑫钧

随着高中数学课堂改革的不断深入，对数学核心素养的关注也更加广泛.数学核心素养包括：数学抽象、逻辑推理、数学建模、直观想象、数学运算、数据分析.那么在高三解题教学中如何落实核心素养呢？笔者以2019年浙江省高考第16题为例，设计了一节解题教学复习课，通过设置问题，铺设台阶，引导学生分析问题、解决问题，不断的提升学生的数学核心素养.下面是课堂简录及笔者的一些思考及体会，不当之处，请批评指正.

一、试题再现

二、试题探究

(一)深刻理解问题本质，培养“数学抽象”核心素养

数学抽象素养是指通过对数量关系与空间形式的抽象，得到数学研究对象的素养.在本题中如何引导学生分析问题，抽象出命题的一般模型，从而把握问题的本质呢？

师：今天，老师给大家带来了一位“朋友”，大家看看熟悉吗？多媒体投影高考题.

生：学生纷纷瞪大了眼睛，不少同学皱起了眉毛，摇摇头表示不认识.

师：大家真的不认识它吗？仔细阅读本题，题干中哪些条件不是很清楚？

师：好的，那我们就来分析一下这个条件.请问f(x)表达式中含有哪些字母？

生：学生很快报出含有a,x.

师：正确！那么请同学想想f(t+2),f(t)的表达式中含哪些字母呢？那么|f(t+2)-f(t)|的表达式则含有哪些字母呢？

生：a,t啊(学生觉得这个问题简单).

生：学生略加思考，回答道：是关于t的函数，参数是a.

师：很好！那哪位同学可以把这样一个问题概括抽象一下？

师：概括的很好！由于f(x)=ax3-x，这样原问题可以抽象为一个什么背景下的问题？

生：三次函数背景下的一个基于存在性条件的不等式成立问题.

评析：通过对高考真题的呈现，激发学生解题欲望，有阶梯的设置问题，由简单问题开始，让所有同学参与到探究过程中，通过不断追问，让学生不断深入的理解试题本质，抽象概括出高考题的一般模型，认识到其实质上就是一到熟题.

(二)合理转换数学问题，培养“逻辑推理”核心素养

逻辑推理素养是指从一些事实和命题出发，依据规则推出其他命题的素养.在获得问题的本质以后，如何去等价转换数学问题呢？在教学过程中，可以向学生提出下列问题：

师：同学们，你们能把S(t,a)化简一下，看看它的庐山真面目吗？

生1：老师，我的化简结果是S(t,a)=|2a(3t2+6t+4)-2|.

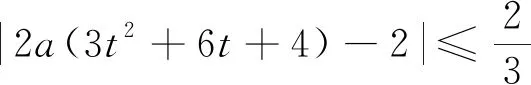
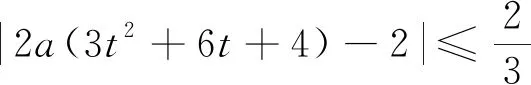
师:很好，这位同学经过思考，发现这个存在性成立问题等价于函数最值问题，这个方向很好.

师：同学们，除了以上转换问题思路外，还能进行其它等价转换吗？

评析:通过引导学生不断的经过推理，拨开问题的面纱，最后将原问题等价转化为我们熟悉的命题或问题，从而获得问题的解法.

(三)明晰算法与算理，培养“数学运算”核心素养

数学运算素养是指在明晰运算对象的基础上，依据运算法则解决数学问题的素养.对“数学运算”的理解不能仅停留在死算的基础上，要在理解运算对象的基础上，合理运用运算法则，正确选择运算方向快速的获得运算结果.这就需要教师在课堂教学过程中舍得给学生运算的时间，展示运算过程，暴露学生运算过程中碰到的运算障碍，引导学生破解障碍，从而培养学生数学运算素养.

师：下面请同学们将试题的具体运算完整表述出来，写好的同学将自己的解答展示一下.

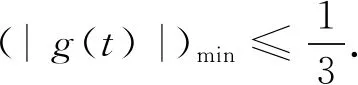
师：两位同学最终都获得了问题的答案，那么问题是不是就结束了呢？大家一起来回顾两位同学的解答过程.第一位同学在对(*)式是如何处理的呢？a>0是怎么得到的？可不可以不求(*)式左边的范围？为什么？

师：第二位同学没有对a<0进行讨论，这样可取吗？理由是什么？

评析：通过对运算过程的追问，让学生经理完整的数学运算过程，在交流展示中暴露运算中的困惑，领会数学运算不仅仅要有算力，更要理解算理，即解决为什么能这样算.事实上运算之中有逻辑推理，通过逻辑推理实现运算的过程，通过逻辑思维优化运算方向与运算过程,只有这样才能真正提高学生的运算能力，培养学生的数学运算素养.

(四)立足联想与表征，培养“直观想象”核心素养

直观想象是指借助几何直观和空间想象感知事物的形态与变化，利用图形理解和解决数学问题的过程.在一些高考数学试题中，问题的条件往往隐含在图形之中，因此，需要运用联想、转换，凭借个体的直观判断，才能发现问题的几何直观，并善于用图形表征数学问题，从而快速的获得问题的解决.那么在解题教学中，如何培养学生的“直观想象”核心素养呢？以本题为例，可以不断的引导学生对式子结构的分析，从而激发学生的联想.

生：学生陷入苦恼之中…….

师：那么大家回顾一下，我们学过那些绝对值函数图像呢？能否对|a(3t2+6t+4)-1|进行处理一下，变成我们熟悉的函数图像呢？

图1

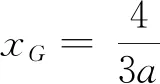
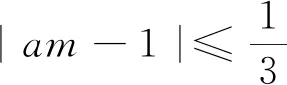
师：这位同学的直观感觉很好，给他点个赞！那么哪位同学可以帮助他完成下面的过程？

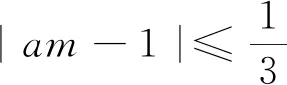
图2

只需要区间

与区间[1,+∞)有交集，即

所以

由于所

a

的最大值，所以对于

a

≤0无需考虑便知

a

的最大值为

评析：依据数学研究的不同分支，数学直观分为几何直观、代数直观等若干类别；还可以依据个体修养的高低，分为从低级到高级的不同层次的数学直观[1].因此在解题教学中让学生通过直观想象引导学生不仅能由数入形，更能从代数中直观出几何，即由数入形的能力,实现高层次的数学直观.

三、结束语

波利亚指出：“货源充足和组织良好的知识仓库是一个解题者重要的资本”.因此要提高学生的解题能力除了丰富学生数学知识，更要让学生形成良好的知识结构，在此基础上才要努力培养学生的数学核心素养.这就需要在课堂教学中要善于设置情景及问题，引导学生思维与表达，给与学生时间运算与展示，提供交流与反思的环境，才能真正地将数学核心素养在解题教学中落实.