无人驾驶模式下电液复合转向系统高鲁棒性控制策略
2019-12-31施国标鞠程赟
施国标 周 倩 王 帅 鞠程赟
(北京理工大学机械与车辆学院, 北京 100081)
0 引言
无人驾驶已成为车辆领域的研究热点,无人车辆转向系统电动化是实现无人驾驶的重要一环。虽然乘用车电动化转向系统,如电动助力转向(EPS)[1]、线控转向系统(SBW)[2],已得到了大量应用,但前轴载荷较大的车辆仍然采用液压助力转向系统(HPS)。传统HPS不具备主动转向功能,无法应用于无人车辆[3]。近些年来,一种融合液压助力转向和电动助力转向(EPS)的电液复合转向系统(Electro-hydraulic hybrid steering system, EHHS)为无人重型车转向系统电动化提供了理想解决方案[4]。与其他转向系统相比,该EHHS转向系统既有驾驶员操纵模式,又有无人驾驶模式,在驾驶员操纵模式下具有节能、随速助力、主动回正等优点[5]。
目前对EHHS系统的研究主要集中在驾驶员操纵模式下的系统参数优化[6]、高速行驶稳定性[7]、理想转向手感控制策略[8]等方面。而EHHS系统用于无人重型车的关键技术是转向角度位置跟踪控制策略,尚未见相关文献报道。当EHHS系统工作在无人驾驶模式时,转向系统对给定理想转角的跟踪效果直接影响车辆路径跟踪效果及整车操纵稳定性[9],对驾驶安全有很大的影响,因此要求系统能快速、准确地跟踪期望转角。而EHHS系统具有较强的非线性,且转向执行过程存在参数扰动,并易受外界干扰影响,采用一般线性控制会存在较大的转角跟踪误差,转角跟踪实时性及对外界扰动的鲁棒性较差[10]。
本文建立考虑系统参数不确定性和外界干扰的转向系统完整非线性动力学模型,设计一种自适应双闭环结构的转角跟踪控制策略,在Matlab/Simulink环境下进行阶跃、正弦、斜坡控制信号的仿真试验,以验证控制策略。
1 转向系统分析及建模
EHHS系统的工作原理如图1所示。在无人驾驶模式时,驾驶员输入方向盘扭矩Th为0,EPS模块的控制器(ECU)接收转向轮理想转角信号,控制电机输出转向力矩Ta。力矩Ta作用在HPS模块的转阀扭杆上端使转阀开启,油液流经转阀开口输入液压缸产生液压助力带动转向横拉杆输出左右拉力,使转向轮转动。
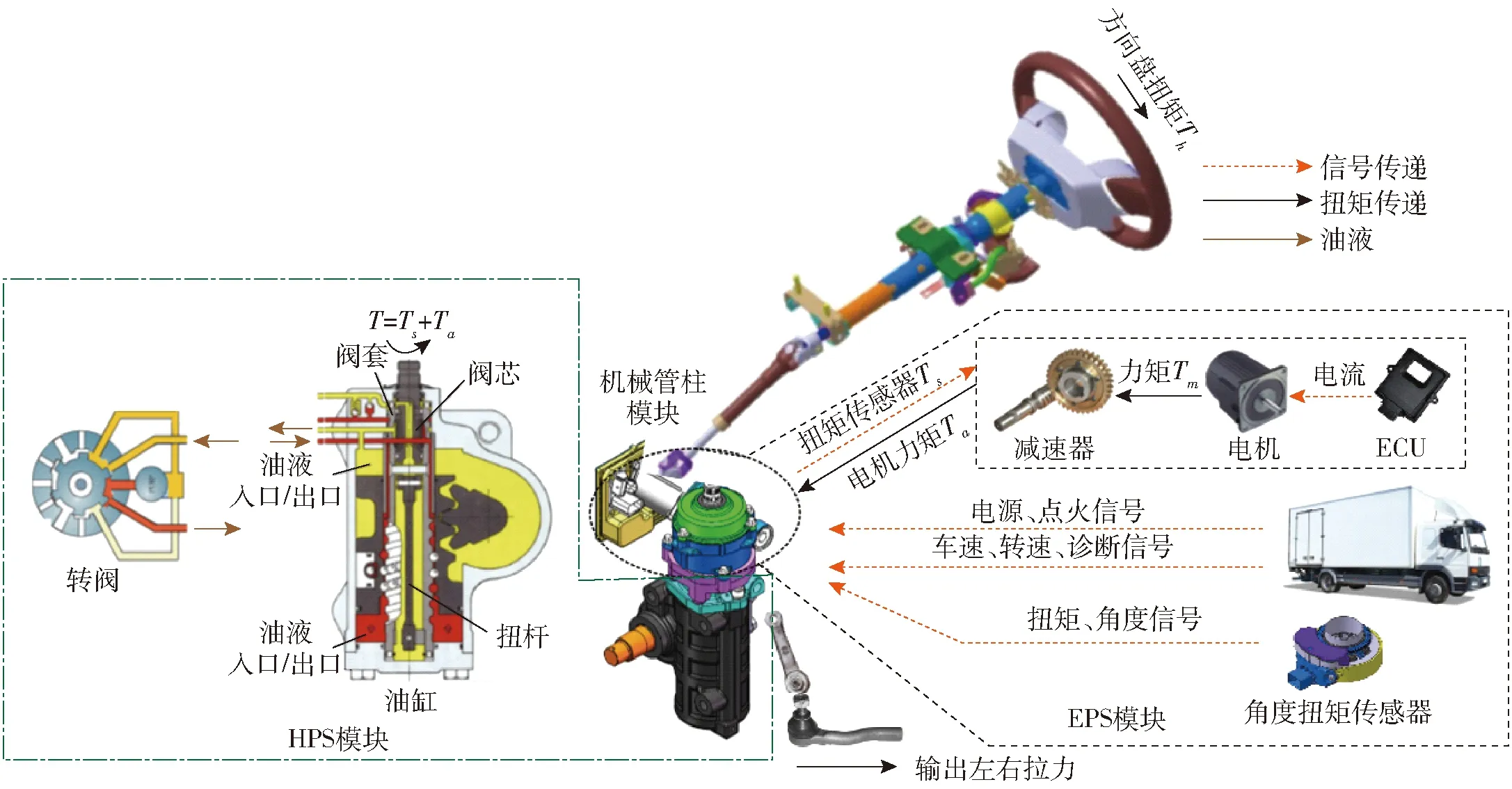
图1 EHHS转向系统工作原理图Fig.1 Schematic of EHHS system
EPS模块输出的电机力矩Ta和HPS模块输出的液压助力FL共同作用克服转向阻力Tr和转向系统内部摩擦力Tf以实现前轮转向,建立转向动力学模型为
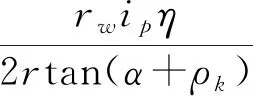
(1)
式中δ——前轮转角
rw——齿扇半径
ip——转向传动机构力传动比
η——转向传动机构的效率
r——螺杆半径
α——螺杆螺旋滚道的导程角
ρk——螺杆螺母副换算摩擦角
Iw——前轮及其固连模块绕主销的转动惯量
m——螺母及其固连部分的质量
Cw——转向系阻尼系数
Cr——活塞的阻尼系数
iw——转向传动机构角传动比
为后续便于建立模型及设计控制器,将式(1)进行变换可得
(2)
其中
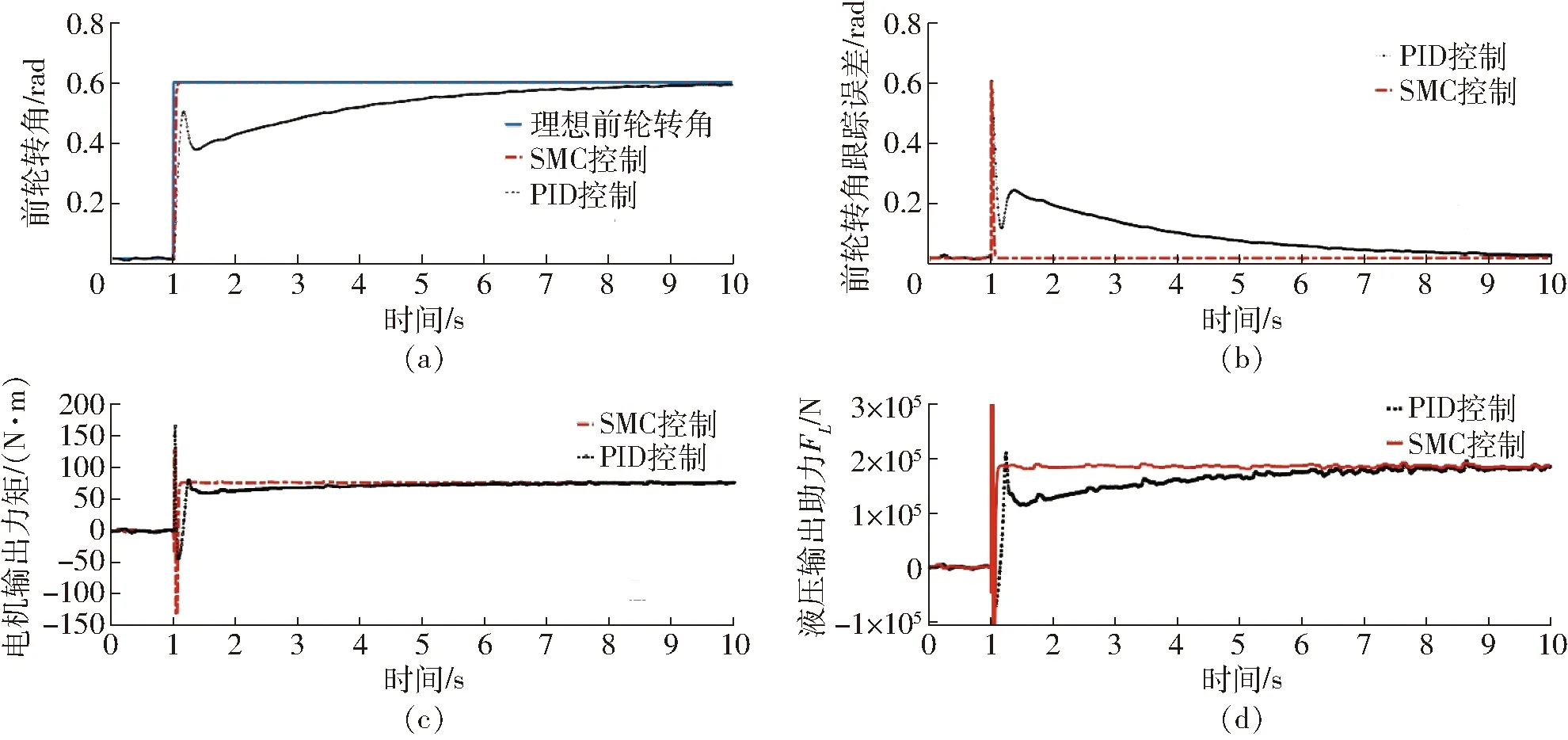
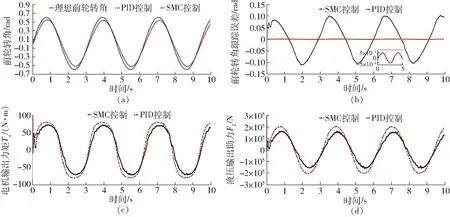
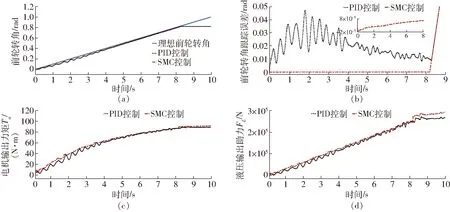
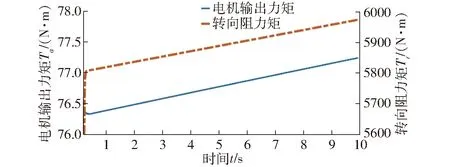
式中确定了转向系统机械结构Mn为定值,此外参数0 考虑系统参数不确定性、外部干扰,以及液压助力系统、路面阻力及转向系统内部摩擦引入的非线性,可得二阶非线性系统为 (3) ΔPn、ΔYn——参数不确定值 Δun——未建模部分(包括侧向风及冰雪路面造成的外界干扰及其他系统内部干扰等) 为进一步明确电机转向助力与转向轮转角的关系,需要对液压助力、转向阻力和系统内部摩擦力做进一步分析。式(3)中,HPS模块输出的液压助力可描述为 (4) 式中A1、A2——各转阀开口面积 Qs——进油口流量 y——活塞位移 Cd——节流孔流量系数 ρ——油液密度 Ap——液压缸活塞有效面积 (5) (6) 其中 ΔθL=Ta/KL 式中A3、A4——各转阀开口面积 W1、L1——阀口预开间隙轴向长度和周向长度 W2、L2——短切口的轴向长度和周向长度 rf——阀芯半径 ΔθL——转阀扭杆转动角度 KL——转阀扭杆刚度 转阀扭杆输出转角与车辆前轮转角存在线性关系 (7) 式中l3——转向节臂长 l1——转向摇臂长 t——转向器螺杆螺距 考虑到轮胎纵向力在左右轮胎载荷差别不大的情况下可忽略不计,假设轮胎侧偏特性在线性范围,本文轮胎转向阻力矩主要包括侧偏力产生的回正力矩和重力产生的回正力矩[11],可得转向阻力公式为 (8) 式中T1——由轮胎侧向力产生的回正力矩 T2——重力产生的回正力矩 ltp——轮胎拖距 lhq——主销后倾拖距 Kf——前轮轮胎的侧偏刚度 β——质心侧偏角 a——质心到前轴的距离 ωr——横摆角速度v——车速 lnq——主销内移量 θ——主销内倾角G——前轴载荷 路面对车辆转向的干扰通过车辆行驶过程中的转向阻力矩Tr传递到转向系统,故将该部分误差归于Δun。 转向系统内部非线性摩擦干扰对系统的影响主要表现为低速出现爬行、稳态出现较大的静差等[12],当前主要是通过建立LuGre模型、Stribeck模型[13]等研究系统摩擦特性,从而建立摩擦补偿机制提高系统动态性能。系统内部摩擦力由Stribeck稳态模型确定,即 Tf(ω)=[Tc+(Ts-Tc)e-(ω/ωs)2+Kv|ω|]sgn(ω) (9) 式中Tc——库伦摩擦力 Ts——最大静摩擦力 Kv——黏性摩擦因数 ωs——Stribeck速率 ω——转动角速度 式(9)中的参数可通过试验方法测得。 基于前述EHHS系统模型分析,提出一种双闭环控制结构的自适应转向角跟踪控制器对EHHS系统目标转角进行跟踪控制,控制框图如图2所示。自适应控制器外控制环通过设计参数自适应率以适应模型参数摄动,采用改进滑模控制由期望转向角计算期望转向力矩。内控制环则利用转向电机PI电流控制器,实现对期望转向力矩跟踪,完成车辆转向操作。 图2 前轮转角跟踪控制策略框图Fig.2 EHHS control algorithm for target steering angle tracking 考虑EHHS系统的非线性及在转向过程中存在的外界干扰,在外控制环中采用改进滑模控制计算期望转向力矩。基于转角跟踪误差设计积分滑模面[14] (10) 其中 式中e(t)——转角跟踪误差 λ1≥0、λ2≥0,为了避免初始误差较大时出现积分饱和现象,系统出现大幅度超调甚至不稳定,λ2不能过大[15]。 在SMC控制系统中系统运动包括两部分[16]:从任意初始状态到达切换面,以及在控制律作用下保持滑模运动。带有不确定性和外加干扰的系统一般采用的控制律为等效控制加切换控制,即 u=ueq+usw (11) (12) 式中L——有界且未知的集中不确定性 (13) 切换控制usw用于实现系统从初始点到切换面的趋近,具有对参数不确定和外加干扰的鲁棒性,采用常值切换控制usw=ksgns(t)。为消减常值切换控制频繁切换引起的抖振[17],引入饱和函数重新定义切换控制usw=ksat(s(t)),其中饱和函数为 (14) 式中φ——边界层厚度 随着φ增大,系统抗抖振能力增强,但是会导致控制精度降低[18]。 在外控制环设计过程中,采用LEE等[19]提出的参数自适应率,以弥补EHHS系统模型参数不确定性。自适应率公式为 (15) (16) 式中ρp、ρY——自适应增益,为常数 综上,可得最终控制律为 (17) 完成控制律设计后,利用Lyapunov原理证明系统渐进稳定性[20],构造Lyapunov函数为 (18) 其中 ΔPn=Pn-nΔYn=Yn-n 假设实际EHHS系统参数Pn、Yn为常数,则推导可得 (19) 对EPS模块中的电机设计了基于稳态的前馈控制器加PI反馈控制器用于控制电机电流,以跟踪来自外控制环的期望转向力矩。根据电机的电压定律可获得电枢回路微分方程为 (20) (21) 对电流偏差采用PI控制,即反馈控制电压为 (22) 其中 ΔI=Ii-Ir 内环电机总控制律为 U=Uf+Ue (23) 式中U——电机电压L——电机电感 R——电机电阻I——电机电流 Kb——电机反电动势 θm——电机输出轴转角 im——蜗轮蜗杆传动比 Ii——理想电机电流 Ir——测得的实际电机电流 通过转角传感器获得控制器所需转角反馈信号,为了避免传感器高频噪声恶化控制效果[21],采用卡尔曼滤波器进行信号处理。考虑传感器只能测得转角信号,建立离散状态方程和观测方程为 (24) 其中 式中Ad——状态转移矩阵 Hd——测量转移矩阵 ΔT——取样时间 wk——过程噪声(假设符合零均值高斯分布) vk——观测噪声(假设符合零均值高斯分布) 先验状态初始协方差为 P0=diag(σ1,σ2,σ3) 过程噪声协方差为 Qk=diag(ζ1,ζ2,ζ3) 观测噪声协方差为 Rk=γ 对状态和方差的时间进行更新,即 (25) 进一步实现状态和方差的滤波更新 (26) 通过调节P0、Qk、Rk使得卡尔曼滤波器达到最优滤波效果。 为了验证各种工况下EHHS转向系统目标转角跟踪控制算法的有效性,在Matlab/Simulink中搭建了控制器—转向系统—车辆的闭环系统模型,并将控制结果与常规采用的PID控制的结果进行对比,分析系统响应速度、转角跟踪精度及抗干扰能力。 对幅值为0.6 rad的阶跃前轮转角信号进行跟踪,获得前轮转角跟踪效果和跟踪误差如图3a、3b所示,自适应双闭环控制器可以更快地跟踪理想前轮转角且稳态误差为零,EHHS系统在0.8 s内能达到理想前轮转角,响应速度明显优于PID控制器。电机经过减速器作用于转向器上的电机力矩对比如图3c所示,液压助力对比如图3d所示,建模时在转向器上输入高斯白噪声模拟外界环境对系统转向的力矩干扰,电机力矩及液压助力对该部分干扰进行了补偿,避免了前轮转角发生抖动。 图3 车速为60 km/h系统阶跃响应曲线Fig.3 Step response curves at speed of 60 km/h 图4 车速为60 km/h系统正弦响应曲线Fig.4 Weave test response curves at speed of 60 km/h 对幅值为0.6 rad、频率为2 Hz的正弦前轮转角信号进行跟踪,以模拟转向轮快速左右摆动的工况。调节PID控制器参数到最优控制效果,转角跟踪对比如图4a所示,相较于PID控制器,自适应双闭环控制器显著减小转角跟踪延迟,提高转角跟踪精度。前轮转角跟踪误差如图4b所示,自适应双闭环控制器控制下误差幅值低于0.001 rad,仅为PID控制的0.1%。两种控制器控制下的电机输出力矩和液压助力如图4c、4d所示,比较可知,自适应双闭环控制器输出的转向力矩更平缓,避免了转向过程中出现抖动。 图5 车速60 km/h系统斜坡响应曲线Fig.5 Stransition test response curves at speed of 60 km/h 对斜率为0.1 rad/s的斜坡转角信号进行跟踪,以模拟转向轮定转速转动。前轮转角跟踪效果对比如图5a所示,受机械限位结构限制,在两种控制器控制下8 s以后转向轮转角都不再变化。调节PID控制器参数使其获得最优控制效果,转角跟踪误差如图5b所示,自适应双闭环控制器控制下转角误差随前轮转角变大而变大,最大误差低于0.000 1 rad,仅为PID控制的0.2%,且不存在大的误差波动,避免了前轮抖动。两控制器控制下EHHS系统输出电机力矩及液压助力如图5c、5d所示,自适应双闭环控制器控制下电机力矩和液压助力更平缓且波动更小,在实际转角控制过程中能获得更好的控制效果。 当EHHS系统参数发生变化时,自适应双闭环控制器及PID控制器的控制效果如图6所示。由图可知,系统参数发生变化会对PID控制系统瞬态响应产生影响;由于控制器中加入了参数自适应控制律,系统参数变化对自适应双闭环控制器控制瞬态响应不会产生影响。 图6 不同转向系阻尼系数下系统的响应曲线Fig.6 Response curves under different conditions with different damping coefficients 重型车辆空载和满载差异较大,由图7可知,车辆转向阻力随着载荷增大而增大,电机输出助力随之增大,载荷变化直接影响转向系统电机力矩特性。由于电机能及时做出反馈,车辆载荷变化对自适应双闭环控制器的控制精度不会产生影响。 图7 车辆载荷变化电机助力特性Fig.7 Motor assist characteristic curves with change of vehicle load 针对新型EHHS系统,考虑系统存在参数扰动、非线性及外界干扰等特点,设计了一种应用于重型车转向系统无人驾驶模式的自适应双闭环结构的目标转角跟踪控制器,并将其与常规采用的PID控制器进行比较。仿真结果表明,该控制器在阶跃、正弦和斜坡等不同的输入信号下都具有优异的控制效果,提升了EHHS系统的瞬态响应性能及稳态性能,对干扰具有较好的补偿效果,且显著提高了跟踪精度,降低了跟踪误差。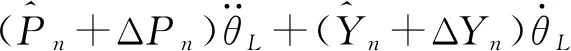
2 转角跟踪控制器设计
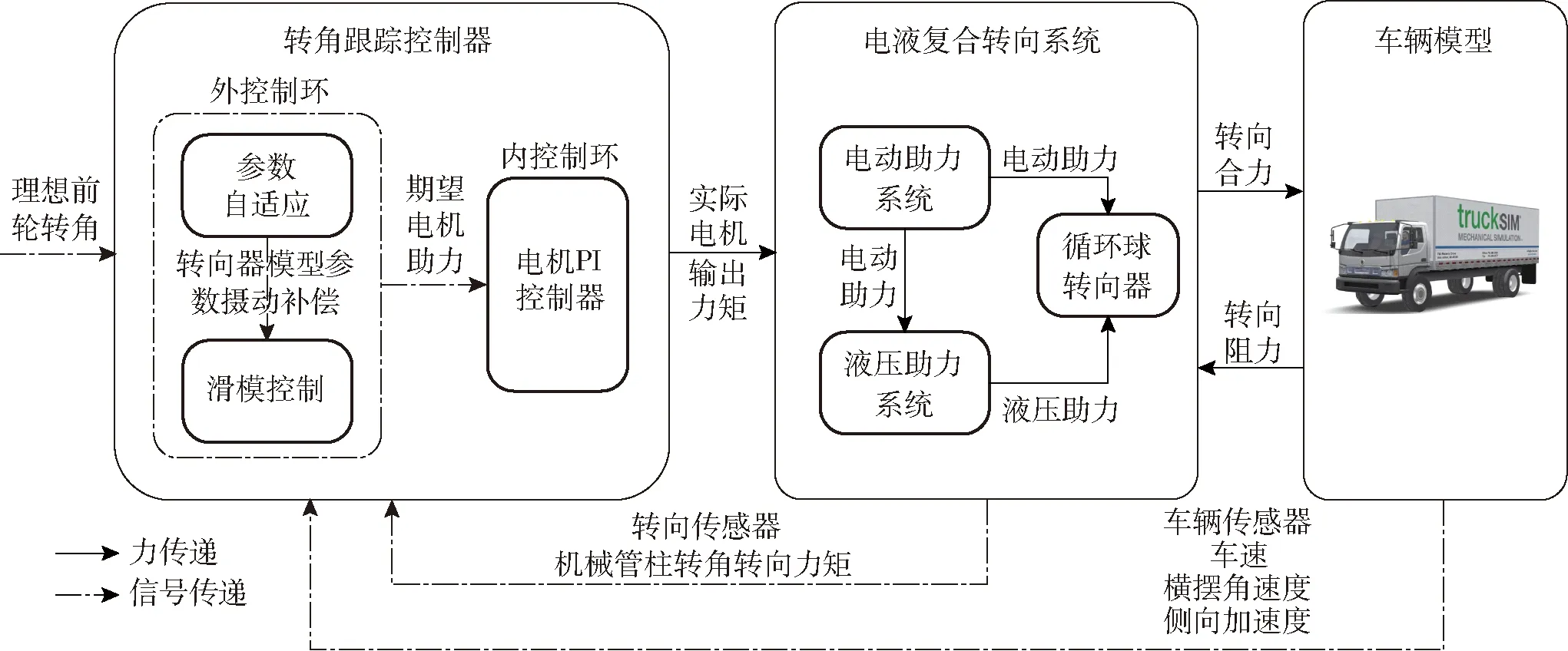
2.1 参数自适应外控制环
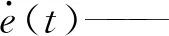
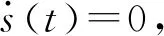

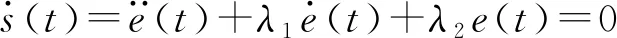
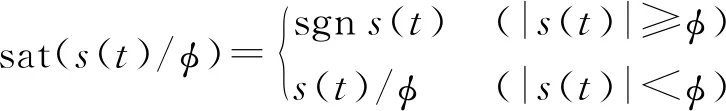
2.2 电机电流内控制环
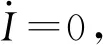
2.3 卡尔曼滤波器设计
3 仿真

4 结束语
