基于分层模型的轮毂电机驱动车辆直接横摆力矩控制
2019-12-31马晓军刘春光陈路明
张 征 马晓军 刘春光 陈路明
(陆军装甲兵学院兵器与控制系, 北京 100072)
0 引言
多轴轮式车辆的行驶工况较为恶劣,通常需要在低附着路面、变附着路面甚至越野条件下保持机动,甚至还要面临紧急变道、小半径转向、高速转弯等特殊工况,因此对其进行动力学控制十分必要[1-2]。传统机械传动的多轮车辆车体结构较为复杂,采用轮毂电机驱动后,车辆底盘结构得到了一定简化,整体结构更加紧凑,各个轮毂电机相互独立,具有可控性强、响应速度快的优点,能够实现驱动/制动状态间的快速切换。此外,电机转速、转矩比较容易获得,便于进行信息交互和信息融合,有利于车辆操纵稳定性控制[3-6]。
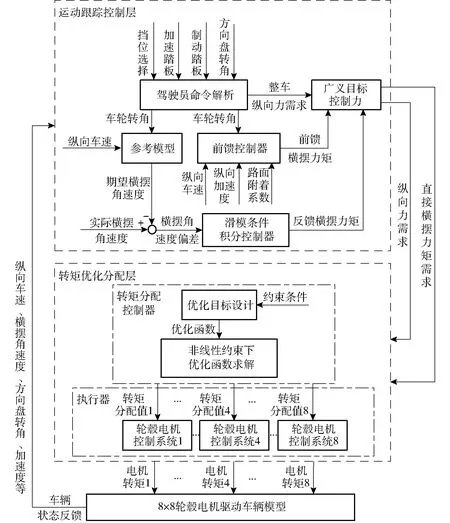
图1 直接横摆力矩分层控制结构Fig.1 Hierarchical structure of DYC
直接横摆力矩控制(Direct yaw-moment control,DYC)是一种根据驾驶员操纵信号和车辆状态信息对控制目标进行跟踪,调整各轮转矩输出值产生附加横摆力矩,进而改善车辆操纵稳定性的控制方法[7-8]。传统DYC系统通过PID控制、最优控制和滑模控制等方法对车辆运动进行跟踪,然后制定一些特定规则对力(力矩)需求进行固定分配,但这类控制系统一般不能根据当前行驶状态充分发挥驱动轮独立可控的优势[9-15]。有学者运用了更加灵活的控制分配法进行DYC研究[16-17]。文献[18]建立了最小化系统能耗目标函数,在既定约束条件下优化不同工况下的经济性,以获得转矩分配值。文献[19]以机动响应速度最快为目标设计优化函数,并转换为数学规划问题求解。以上方法在四轮轮毂电机驱动车辆中取得了较好的整车运动控制效果,但尚未完全扩展到多轮轮毂电机驱动车辆。
本文建立基于分层模型的某型8×8轮毂电机驱动车辆DYC系统。上层为运动跟踪控制层,设计基于驾驶员命令解析的前馈控制器,并且利用滑模条件积分控制器进行反馈控制,追踪车辆期望运动。下层为转矩优化分配控制层,构建以改善车辆操纵稳定性为目标的优化函数,充分结合电机驱动能力和行驶路面情况等约束条件,将上层得到的广义目标控制力分配至各个车轮,并采用实车试验对控制策略进行验证。
1 DYC系统结构
DYC分层控制结构如图1所示,驾驶员根据当前路径信息和行驶状态对被控车辆进行操控,上层为运动跟踪控制层,对驾驶员命令进行解析,计算整车纵向力需求,结合路面情况和状态参数设计前馈控制器得到前馈直接横摆力矩;同时基于参考模型推导期望横摆角速度,设计滑模条件积分控制器进行反馈控制,使横摆角速度追踪期望值,得到反馈横摆力矩。下层根据上层广义目标控制力进行转矩优化分配,建立目标优化函数,并综合轮毂电机驱动能力、路面状况等约束条件进行目标函数求解,进而得到各轮分配力矩,最后行驶状态信息实时反馈至上层控制器,构成了完整的直接横摆力矩控制系统。
2 运动跟踪控制策略
2.1 车辆参考模型
对车辆进行行驶控制时,需建立期望动力学模型,在此基础上制定车辆稳定性控制目标[20]。由于车辆稳定行驶的状态一般可以用单轨二自由度模型的稳态响应表示,因此将车辆线性二自由度模型作为运动跟踪控制层的参考模型。
侧向运动时,有
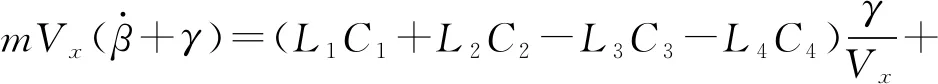
(C1+C2+C3+C4)β-C1δ1-C2δ2
(1)
横摆运动时,有
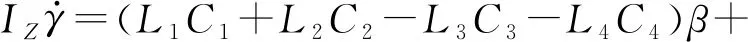
(2)
式中Vx——车辆速度,m/s
γ——横摆角速度,rad/s
m——整车质量,kg
β——质心侧偏角,rad
δi——第i个轴车轮转向角,rad
Li——第i轴与质心处的距离,m
IZ——转动惯量,kg·m2
Ci——第i轴车轮的侧偏刚度,N/rad
MZ——直接横摆力矩,N·m
转向角关系为
δ2=asδ1
(3)
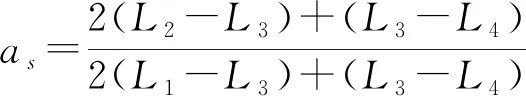
(4)
式中as——比例系数
2.2 前馈控制器设计
2.2.1前馈系数
前馈控制可以在失稳前对车辆运动状况进行预先判断,根据驾驶员命令获得前馈补偿横摆力矩。
前馈控制横摆力矩
MZF=Kfδ1
(5)
式中Kf——前馈增益系数
横摆运动时,有
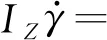
(Kf-L1C1-L2C2as)δ1
(6)
施加前馈控制后,车辆系统状态方程为
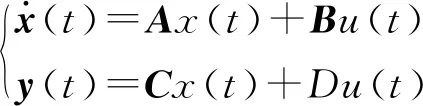
(7)
其中
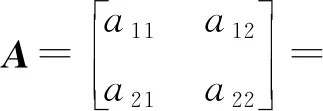
对式(7)进行变换,δ1输入到γ响应的传递函数为
(8)
式中S——拉普拉斯算子
令S=0,得到车辆系统对δ1的稳态增益,即
(9)
计算得到前馈增益系数
(10)
2.2.2前馈控制自适应切换条件
一般情况下,当车辆正常行驶时,适当施加前馈横摆力矩有利于改善车辆操纵稳定性;然而极限工况时,前馈控制容易加剧车辆失稳现象。8×8轮毂电机驱动车辆行驶时,需要面对各种复杂路况,因此需设计前馈控制的介入和退出条件。
经过前期一系列仿真试验发现,车辆的稳定性裕度与侧偏工况有关,车辆处于小侧偏工况时,稳定性裕度良好,可以施加前馈控制;而大侧偏条件下,一般不进行前馈控制,为满足行驶控制需求,可对其单独施加反馈控制。鉴于此,本文设计运动跟踪控制层的前馈控制介入系数kZF,根据不同行驶工况运用自适应切换调节kZF的取值,如图2所示。图中ay为侧向加速度,m/s2,μ为当前路面附着系数。
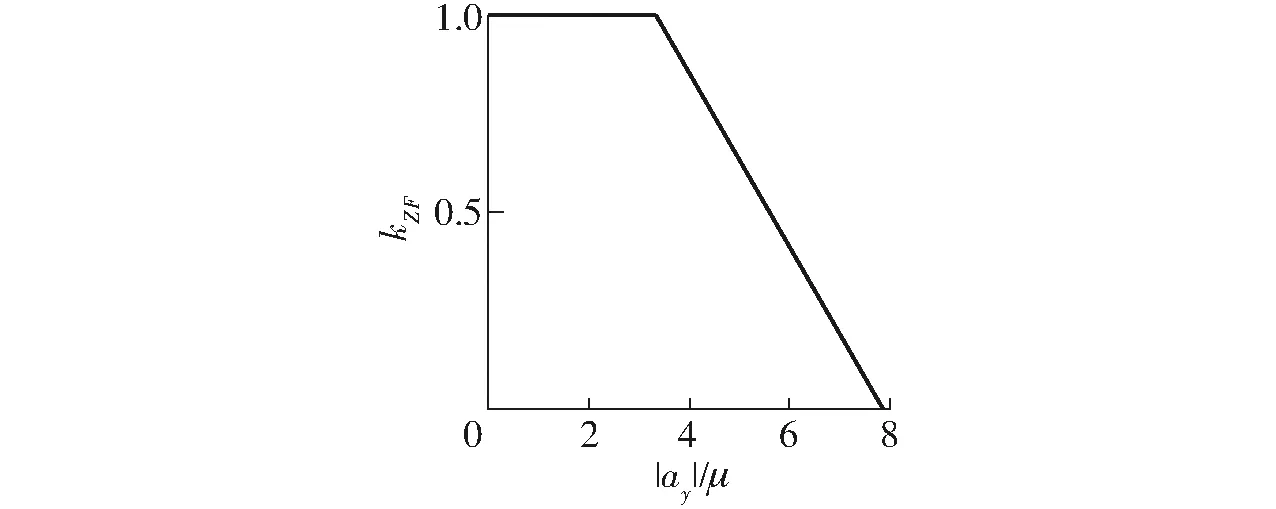
图2 介入系数自适应切换Fig.2 Adaptive switching of intervention coefficient
当|ay|/μ≤3.6时,kZF=1,此时前馈控制完全介入; 当|ay|/μ≥7.8时,kZF=0,此时前馈控制完全退出; 3.6<|ay|/μ<7.8区间为过渡过程,可以消减前馈控制切换过程引起的系统抖振问题。
2.3 反馈控制器设计
2.3.1控制变量期望值计算
根据参考模型,由式(9)和式(10)推导横摆角速度稳态值,即
(11)
其中
Le=
(12)
(13)
式中Le——等效轴距K——稳定性因数
根据路面情况,需要满足约束条件
(14)
式中c——车辆安全性能系数
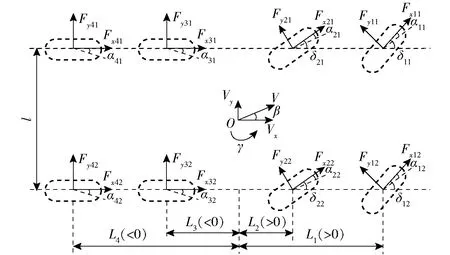
根据文献[21],通常将c作为权衡车辆转向性能和安全性能的权重,且0 综上,理想横摆角速度为 (15) 2.3.2滑模条件积分控制器设计 针对研究对象部分参数的非线性特性、时变特性和外界干扰,设计反馈控制与前馈控制互补,具体过程如下: 横摆角速度误差为 eγ=γ-γd (16) 建立滑模控制器的滑模面 s=eγ=γ-γd (17) 采用等速趋近律,令 (18) 式中kγ——等速趋近律参数,且kγ>0 对式(16)求导,并代入式(17)中,有 (19) 结合轮毂电机驱动车辆横摆运动方程,得到传统滑模控制器反馈控制横摆力矩输出,即 (20) 采用滑模控制可以使系统具备较好的鲁棒性,但在滑模面附近的非连续特性造成的控制信号抖动[22]。针对滑模面附近抖振和积分饱和问题,基于“积分分离”的思想,引入条件积分器,进一步对滑模控制进行改进,设计滑模条件积分控制器(Sliding mode control with conditional integrator, SMC&CI),改善系统响应特性和控制效果。 在式(16)基础上,增加条件积分项 sc=eγ+kqσ (21) (22) 其中 sc(eγ,σ)=0 式中σ——误差积分,且σ(0)≤ε/kq kq——调节参数,且kq>0 ε——滑模切换边界层宽度,且ε>0 sc——新增滑模面 用饱和函数sat(sc/ε)代替sgn(sc/ε),即 (23) 则滑模条件积分控制器输出的反馈横摆力矩为 (24) 系统稳定性证明参照文献[23]。 综上,得到运动跟踪层总直接横摆力矩 MZ=kZFMZF+MZB (25) 非线性三自由度车辆模型如图3所示。图中l为轮距,m,Fxij、Fyij为纵向力、侧向力,N。 图3 非线性三自由度车辆模型Fig.3 3-DOF nonlinear dynamics model of vehicle 设上层输出的广义目标控制力和各车轮纵向力的关系可表示为 Y=B′X (26) (27) (28) (29) 式中Y——广义目标控制力 X——控制输入B′——控制矩阵 设计动力学需求目标优化函数为 (30) (31) 式中Hy——需求目标权重矩阵 根据文献[24],定义轮胎负荷率为 (32) 式中ρij——单个轮胎的负荷率,% Fzij——轮胎垂直载荷,N 设计电机转矩分配目标函数为 (33) (34) 式中Hx——二次优化权重矩阵 Tij_d——各轮分配的转矩,N·m 综合考虑优化目标函数式(30)和式(33),为了精简算法并同时对两个目标函数进行优化,将二者合并成转矩分配综合目标函数 (35) 由于满足驾驶员的需求比降低失效车轮使用等级更重要,设定罚因子ψ为一个很大的正数,即ψ≫1。 Fxij受到电机能够提供的最大转矩约束,即 (36) 式中Tijmax——电机最大转矩,N·m r——车轮半径,m Fxij和Fyij受到轮胎状态、垂向载荷Fzij及路面因素影响。假设纵/横向峰值附着系数均为μ,当纵滑和侧滑同时发生时,纵向力Fxij和侧向力Fyij之间存在着复杂耦合关系,有 (37) 则受摩擦圆限制,Fxij需要满足 (38) 优化目标函数J可以改写为 (39) 将待解决目标优化问题转换为二次规划问题,即 (40) 利用起作用集合法对二次规划问题进行求解,步骤为: 定义起作用集合W,它包括全部起作用的约束。 (1)令X=X0为可行起始点,该点满足全部约束条件。 (2)对于i=0,1,2,…,n,依次迭代xi,寻求最优校正量p,将W中不等式约束考虑成等式约束,忽略其他约束。即 (41) (3)判断xi+p是否为可行点,如可行,执行步骤(4);如不可行,执行步骤(5)。 (4)令xi+1=xi+p,计算拉格朗日乘子λ (42) 其中,D0为D中起约束的条件。 如果λ≥0,xi+1就是最优解,停止计算。否则,从W中移除λ中最小的一个值对应的约束,重新进入步骤(2)。 (5)令xi+1=xi+p,将对xi+1起作用的约束加入W,进行步骤(2)。 步骤(1)~(5)构成了一套完整的求解算法。上述目标函数的解既能满足整车力(力矩)需求又能降低轮胎负荷率的最优解。 图5 高附着路面连续转向行驶Fig.5 Continuous steering on high adhesion road 采用某型8×8轮毂电机驱动车辆开展实车试验对控制策略进行验证。其中,方向盘转角信号和状态信息(加速度、横摆角速度等)可分别由图4a所示方向盘转角传感器、图4b所示状态信息采集盒获得;试验过程中的状态信息和数据可通过图4c所示显控终端进行实时监测、反馈和存储记录。样车部分参数取值和试验条件设置分别如表1、2所示, 图4 试验设备Fig.4 Test equipment of real vehicle 采集的信号分别如图5a和图6a所示,试验结果如图5b~5d和图6b~6d所示。 表1 车辆部分参数Tab.1 Parameters of vehicle 表2 试验条件Tab.2 Conditions of sample vehicle 图6 低附着路面双移线行驶Fig.6 Double shifting on low adhesion road 试验车辆在μ=0.8的路面进行连续转向运动,图5a和图5b分别为转向盘操纵信号和横摆角速度偏差,可以看出,与无DYC车辆、采用滑模控制车辆相比,施加分层DYC车辆的横摆角速度更加趋近于理想横摆角速度,最大横摆角速度偏差能够控制在理想横摆角速度的6%左右,这说明在给定相似驾驶信号情况下,分层DYC提高了车辆姿态保持能力和运动跟踪能力;由图5c可知,施加分层DYC后,下层转矩优化分配控制效果明显,车辆连续转向行驶时,实现了8个轮毂电机转矩的差异分配;图5d表明,与转矩平均分配方法相比,采用转矩优化分配后,车辆总轮胎负荷率更加稳定,并且在整体趋势上明显降低。 由图6a、6b可知,由于路面附着条件限制,无控制车辆的横摆角速度与其理想值间存在较大差异,容易发生失稳现象,滑模控制可以在一定程度上减小横摆角速度偏差,而施加分层DYC后,横摆角速度偏差进一步减小,最大横摆角速度偏差在理想横摆角速度的9%左右,车辆循迹能力得到了有效提高;图6c表明,转矩优化分配控制器根据车辆行驶状态对前、后轴电机的转矩进行调整,并且使得外侧电机转矩明显小于内侧电机转矩;由图6d可知,分层DYC的下层控制器将车辆总轮胎负荷率控制在较低水平,与转矩平均分配的车辆相比,转矩优化分配增加了轮胎纵向力输出储备,使车辆稳定裕度得到了提高。 (1)设计了上层前馈控制与反馈控制结合的运动跟踪控制方法,通过基于车轮转角的前馈控制器,提高跟踪目标稳态增益;考虑积分饱和影响,利用滑模条件积分控制对行驶过程中的横摆角速度进行反馈调节。 (2)下层建立了基于稳定性的目标优化函数,根据电机驱动能力、路面情况设定约束条件,利用起作用集合法进行求解,实现了转矩优化分配。 (3)依托某型8×8轮毂电机驱动样车开展实车试验,结果表明,该策略具有可行性,在不同工况下都能较为精确地控制车辆姿态和运动轨迹,并且有效降低了轮胎负荷率,改善了轮胎纵向力输出储备和车辆稳定裕度,具有良好的稳定性控制效果。3 转矩优化分配策略
3.1 优化目标函数
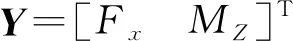

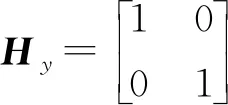
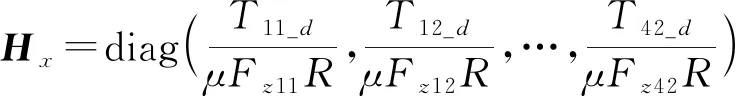
3.2 优化分配约束条件
3.3 基于二次规划的控制分配求解算法
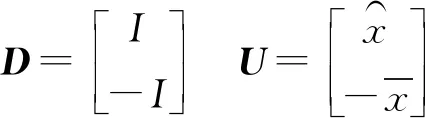
4 试验验证及分析
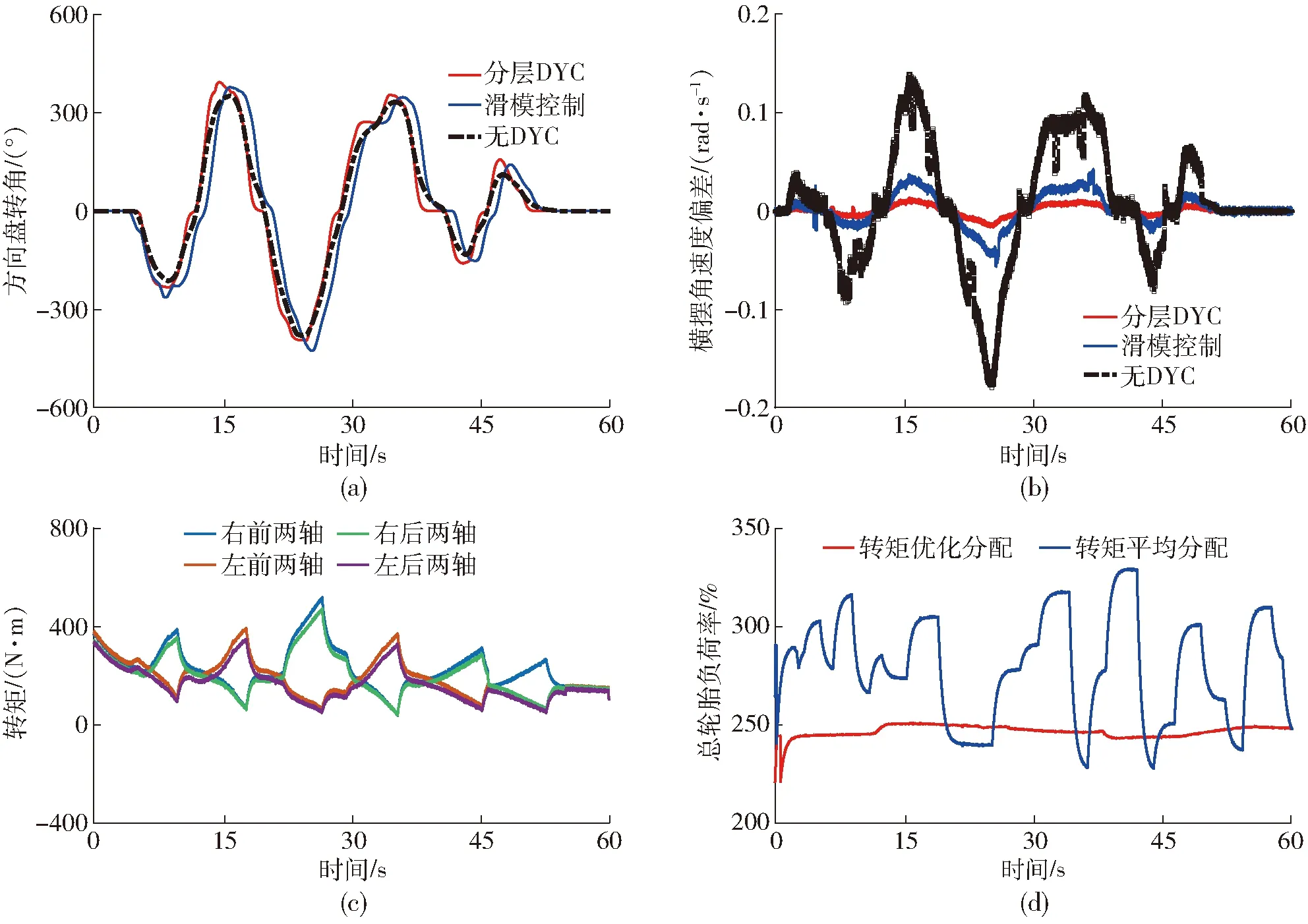



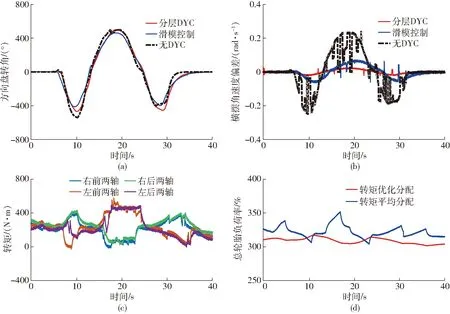
5 结论
