正交变换在几何学中的应用

张立新

(鞍山师范学院 数学与信息科学学院,辽宁 鞍山 114007)

在高等代数的后续学习中，引入正交变换，从而让学生了解到化二次型为标准形的方法不仅有配方法、合同变换法，还有正交变换法.正交变换是代数学中常用的线性变换，它具有鲜明的几何特征.尽管如此，初学者对其在几何学中的应用还是比较模糊，同时这方面的研究文献也偏少，鉴于此，本文从3个方面论述正交变换在几何学中的应用.

1 正交变换的相关理论

1.1 正交变换

欧式空间V的线性变换σ，如果它保持向量的内积不变，即对于任意的α,β∈V,都有(σ(α),σ(β))=(α,β)，则称σ为正交变换[1].正交变换可以从以下几个方面来加以刻画：

设σ是n维欧式空间V的一个线性变换，于是下面4个命题是相互等价的：

(1)σ为正交变换；

(2)σ保持向量的长度不变，即对于任意的α∈V,|σ(α)|=|α|；

(3)如果ε1,ε2,…,εn是标准正交基，那么σ(ε1),σ(ε2),…,σ(εn)也是标准正交基；

(4)σ在任一组标准正交基下的矩阵是正交矩阵.

1.2 正交矩阵

n阶实方阵A，如果满足A′A=E，则称A为正交矩阵[2].

n阶正交矩阵A具有如下性质：

(1)A为可逆矩阵，且A-1=A′；

(2)A′也为正交矩阵(从而A-1也为正交矩阵)；

(3)对任意n维列向量X，AX保持向量X的长度，即|AX|=|X|；AX和AY保持向量X和Y的内积，即(AX,AY)=(X,Y)；

(4)A的n列(行)向量构成Rn的一个标准正交基.

欧式空间中，在标准正交基下，正交变换与正交矩阵是一一对应关系.一个正交变换对应一个正交矩阵；反之，一个正交矩阵对应一个正交变换.

如果A是正交矩阵，那么AA′=E可知|A|=±1.因此，行列式等于+1的正交变换通常称为第一类正交变换(也称为旋转的)；行列式等于-1的正交变换通常称为第二类正交变换.

2 正交变换在几何学中的认识

正交变换是欧式空间保持向量内积不变的线性变换.它不仅保持向量的长度不变，而且还保持向量的夹角不变.二维或三维空间中的旋转变换、关于某一条直线或平面的对称变换都是正交变换.投影变换、平移变换不是正交变换.

例1平面上过原点的所有向量构成实数域上二维线性空间R2.设σ是平面上的向量绕坐标原点按逆时针旋转θ角的旋转变换,

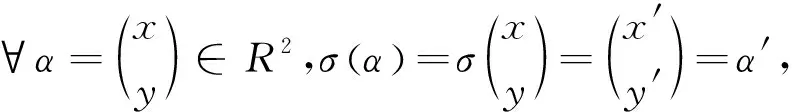
证明

记

σ(k1β1+k2β2)=k1σ(β1)+k2σ(β2)，

所以旋转变换σ是正交变换.

证毕

旋转变换不仅是欧式空间的线性变换，而且还保持向量的内积不变(即保持向量的长度不变，保持向量的夹角不变)，因而它是正交变换.由于旋转变换的矩阵的行列式等于+1,所以旋转变换是第一类正交变换.

解

σ(β1)+σ(β2)=β1+β2+2α0≠σ(β1+β2)，

故平移变换不是线性变换，所以它不是正交变换.

证毕

平移变换虽然保持向量的长度不变，保持向量的夹角不变，但它不是线性变换，因而平移变换不是正交变换.

例3设η是n维欧式空间V的一个单位向量，对任意α∈V，定义线性变换σ(α)=α-2(η,α)η,证明σ是正交变换(这样的正交变换也称为镜面反射变换).

证明对任意

α,β∈V,(σ(α),σ(β))=(α-2(η,α)η,β-2(η,β)η)=

(α,β)-4(η,α)(η,β)+4(η,α)(η,β)(η,η)=(α,β)，

故σ是正交变换.

证毕

假设η是平面π的法线方向，(η,α)η是向量α在η方向的投影向量，如图1所示，于是σ(α)与α关于平面π对称，因此正交变换σ(α)=α-2(η,α)η也称为镜面反射变换.

镜面反射变换是最简单的一类正交变换.在n维欧式空间V中，任一正交变换都可表示成有限个镜面反射的乘积.

图1 镜面反射变换镜

3 正交变换在几何学中的应用

正交变换是线性变换的一种，它从实内积空间V映射到V自身，保持变换前后内积不变.它应用在几何学上就是保持变换前后图形的不变性，这是正交变换的优势，从而达到了判断二次曲面类型、辨明二次曲面形状的目的.

任意一个实二次型

例4方程

表示何种二次曲面？

解首先利用正交的线性替换将实二次型

化为标准形

A的特征多项式为

A的特征值为λ1=λ2=2,λ3=-7.

可求得对应的λ1=λ2=2特征向量分别为p1=(-2,1,0)′,p2=(2,0,1)′，将其正交化

再单位化得

故正交变换

将实二次型f(x1,x2,x3)化为标准形

可知方程

表示的曲面为旋转单叶双曲面.

分析：先判断二次曲面的形状，然后再求其所围成的几何体的体积.

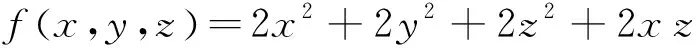
A的特征多项式为

A的特征值为λ1=1,λ2=2,λ3=3.

由特征值再解出特征向量，再单位化得正交矩阵为

故正交变换

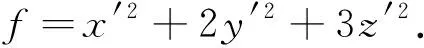
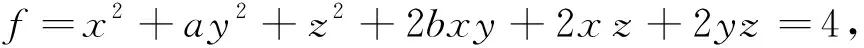
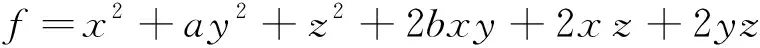
因为二次曲面f(x,y,z)=4经正交线性替换化为椭圆柱面v2+4w2=4,所以方程v2+4w2是二次型f(x,y,z)的标准形，而标准形的矩阵为

从而A与Λ相似，故|λE-A|=|λE-Λ|，展开得

-λ3+(a+2)λ2+(b2-2a+1)λ-1+2b-b2=-λ3+5λ2-4λ，

比较同次幂系数得

可求得A的特征值为

λ1=0,λ2=1,λ3=4,

其特征向量分别为

p1=(-1,0,1)′,p2=(1,-1,1)′,p3=(1,2,1)′，

再单位化得

所用的正交矩阵

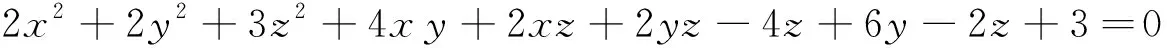
分析：可先通过正交变换再通过平移变换，将二次曲面方程化成标准形式的方程.

解

则二次曲面方程为X′AX+B′X+3=0.

A的特征值为λ=2,5,0,对应的单位特征向量为

则经正交变换X=TY，即

二次曲面方程化为

Y′T′ATY+B′TY+3=0，

即

再经平移变换

综上所述，二次曲面方程如果是二次型方程，可利用正交变换化实二次型为标准形，来判断二次型曲面的形状.更一般地，如果二次曲面方程中不仅含有二次项，而且还含有一次项，通常可通过正交变换再通过平移变换，将二次曲面方程化成标准形式的方程[3]，从而判断了二次曲面的形状，达到了模糊问题清晰化的目的.