变风量空调系统用非线性模型预测控制方法研究

(1 上海交通大学制冷与低温工程研究所 上海 200240； 2 上海应用技术大学城市与建筑学院 上海 201620;3 上海真聂思楼宇科技有限公司 上海 200063)

建筑行业的能源消耗逐年增加,占到发达国家总能耗的20%～40%。近几十年来由于建筑面积的扩大和对热舒适性需求的提高，能源消耗呈现增长趋势[1]。由于HVAC系统是建筑物中主要的耗能设备，因此科研人员在HVAC系统节能方面进行了很多研究。变风量(VAV)空调系统最初在20世纪60年代中后期提出，并且由于其在HVAC系统中的节能潜力，在20世纪80年代早期在英国和欧洲其他国家得到普及。

VAV系统通过在热负荷变化时改变进风流量使室内空间维持恒定温度。VAV系统中最常用的控制方法是基于比例积分(PI)控制器的定静压方法[2]。基于PI控制器根据室内空气温度与其设定点之间的偏差调整阻尼器；根据阀门前的空气静压与其设定点之间的偏差调节风机转速，通常选择最不利的终端静压作为静压设定点。但静压设定点大多高于实际所需的静压值，这既导致很大的能量损失，也增加了系统噪声。为了克服定静压方法的这一缺点，陈华等[3]提出了变静压方法。变静压方法根据实际情况调整静压设定值，以此降低静压损失和风机能耗[4]。但定静压和变静压方法都需要两个带PI控制器的反馈控制回路(一个用于控制终端阻尼器，另一个用于控制风机转速)，这不可避免导致系统调节的延迟、过调和较差的鲁棒性等问题，特别是对于大的干扰量。针对反馈控制的缺点，Dai Binwen等[4]提出总风量控制方法，以避免变静压和定静压方法中使用静压设定点。在总风量控制中，首先根据所有房间的负荷需求，获得相应的总送风量；然后通过调节风机转速来满足送风量需求。虽然总风量控制无需安装静压传感器，少了一个反馈回路(风机转速由反馈变为前馈)，但终端阻尼器的控制依然需要一个闭环反馈。与定静压和变静压方法相比，总风量方法没有完全解决延迟、过调和鲁棒性等方面的问题。同时，为了计算所有房间的负荷，需要在每个末端加装风量传感器或风速传感器，这也增加了系统的建造成本。基于模型的预测控制(MPC)可能是解决定静压、变静压和总风量控制中存在的问题的有效方法[5]。

模型预测控制属于监督控制方法，主体包括预测模型和滚动优化[6]。其中预测模型有3种类型：物理模型(白箱模型)，数据驱动模型(黑箱模型)和混合模型(灰箱模型)。物理模型的复杂性使其难以应用于实际系统。例如，基于物理的预测模型需要许多传感器，这不可避免地增加了控制系统的投资；物理模型校准也面临挑战，因为需要识别大量参数。对于数据驱动模型，只需得到足够多的训练数据，就能找到系统输入和输出变量之间的关系[7]。灰箱模型以物理模型为框架，通过拟合得到详细的模型参数。灰箱模型与数据驱动模型相比，可提供更好的泛化能力；与物理模型相比，具有更好的准确性，但开发难度也最大。为了开发灰箱模型，需要了解系统的基础物理特性和输入、输出数据。对于一些HVAC子系统，基础物理结构可能非常复杂，而对于其他系统，输入输出数据可能不易获得，因此灰箱模型难以开发[8]。神经网络模型(ANN)作为一种数据挖掘模型，非常适合非线性系统建模。有许多类型的ANN结构，如多层感知器(MLP)[9]、径向基函数(RBF)[10]、具有外生输入的非线性自回归模型(NARX)[11]等。在本研究中，NARX用于预测系统的未来状态，因为与其他结构的神经网络相比，它在解决数据相关性较大的问题上具有更好的性能[12]。

对于滚动优化，由于VAV系统是非线性系统，采用的神经网络模型也是非线性模型，所以优化问题是非线性和非凸的。遗传算法(GA)等全局优化方法[13]可以解决非线性优化问题，但存在收敛慢和计算复杂性的问题。考虑到MPC模型的复杂性和非线性，本研究采用粒子群优化算法(PSO)[14]，其具有收敛速度快，计算时间短以及全局和局部优化之间的平衡机制等优点。另外，VAV系统中的优化问题是包括风机转速和多个风阀末端的多目标优化问题，通过将不同的权值分配给成本函数的多个目标，将多目标优化转换为单目标优化问题[15]。且随着权值的改变，MPC能够实现不同的功能。

近年来，在VAV系统中，已有以数据挖掘模型作为内部模型和用智能算法进行优化的研究。Liang Wei等[16]利用ARMAX模型对回风温度和回风量进行预测，并用拉格朗日乘子法优化出回风和新风比、新风量和送风温度。该方法虽然节能，但未加入末端风阀，控制精确度不高；选取各个房间的加权平均温度作为模型的输入，会导致其中一些房间在大扰量下的温度失调。Wei Xiupeng等[15]采用多层感知机作为预测模型，PSO优化送风温度和风阀的设定静压值。这种控制方法没有改变系统结构，依旧采用传统的反馈控制，通过优化的送风温度和静压设定值来实现节能。但该方法未解决系统的延迟、过调等诸多反馈系统中存在的问题，且系统中大量传感器的使用增加了建造成本。A. Erfani等[17]采用NARX模型作为预测模型，GA优化风机启停、风阀开度和水阀开度。本文系统主要通过优化风机的启停实现节能，但严格意义上是一种定风量系统。

本文提出一种用于变风量(VAV)系统的非线性MPC，该非线性MPC采用具有外部输入的非线性自回归网络(NARX)和粒子群优化算法(PSO)，NARX旨在预测VAV系统的受控参数(室温)，PSO作为优化器，以获得VAV系统的最优控制变量。

1 系统描述

本文的控制方法通过搭建的VAV实验进行验证，实验系统如图1所示。该系统主要由变频风机、水-空气换热器、变频空气源热泵、冷水泵、3个带VAV box(型号：TVS-A-250)的房间组成。 主要测量仪器包括：温度传感器(精度：±0.1 ℃)用于温度测量、ABB变频器用于风机频率调节(精度：±0.1 Hz)、电能表(精度：±0.01 kW·h)用于测量风机能耗、SIEMENS PLC(型号：S7-1200)用于数据的记录、处理和反馈输出。

影响房间热特性的主要变量是送风量和送风温度。送风量可通过风机转速和VAV box的阀门开度调节。送风温度受到诸多因素的影响，包括AHU的进水条件和进气条件，无法直接、准确地获得。因此，送风温度(Tsa)被认为是干扰量，风阀开度(P)和风机频率(f)被选作VAV系统的控制变量。系统中还有一些扰量，包括太阳辐射、室外温度。由于实验房间采用彩钢板搭建，中间填充隔热材料且无窗，因此房间的隔热性能强，透光性差。并且在实验过程中，室外温度变化较小，所以太阳辐射和室外温度均被忽略，不作为模型的输入变量。

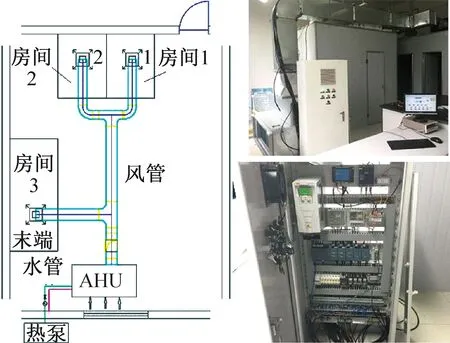
图1 VAV实验系统

2 MPC设计

MPC通常包括预测模型和滚动优化。NARX预测模型被用于预测房间的回风温度，PSO被用于寻找优化的控制变量(u)：包括风机频率(f)和各个房间的风阀开度(P)，以最小化成本函数。

2.1 NARX模型

NARX模型是一种周期性多层感知机(MLP)。与其他结构的神经网络相比，它在解决数据相关性较大的系统上(即房间温度在前后时间上呈现相关性)具有更好的性能。NARX模型如式(1)所示：

(1)

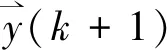
图2 NARX神经网络结构

对于多层感知机的参数设计[18]，通过对在模拟系统中得到的大量模拟数据进行训练，得到最佳的神经元数量为30。继续增加神经元并未提升网络的精度，反而大大增加了训练时间。对于NARX的延迟步数d的选取，通过对模拟数据进行训练，得到d=2，此时NARX神经网络可有最好的精度。

2.2 滚动优化

MPC不是采用同一个的全局最优目标，而是采用滚动的有限时域优化策略，在每个时间域内重复优化成本函数，从而得到最优化的控制变量。成本函数的组成可以是跟踪误差、能耗、其他代替参数或其组合形式。本文中，预测房间温度的跟踪误差是成本函数的一部分，另一部分则考虑风机能耗。在满足热舒适性的前提下，使用更小的风机频率以节省电能，使用更大的阀门开度来减小静压损失和噪声。成本函数如式(2)所示：

(2)

参考轨迹是为了避免控制过程中出现输入和输出的急剧变化，尽量使房间温度y(k)沿着较为平缓的曲线达到设定值S(k)，表现为跟踪误差呈指数级趋势减小。参考轨迹如式(3)所示：

yr(k+i)=(1-αi)S(k)+αiy(k)

i=1,…,Nl

(3)

式中：α(0<α<1)为柔化系数，α越大表示控制稳定性更好，但也意味着更慢的响应速度；Nl为预测域。由于本文中的系统热惯性相对实际的大建筑系统较小，α取0.3。

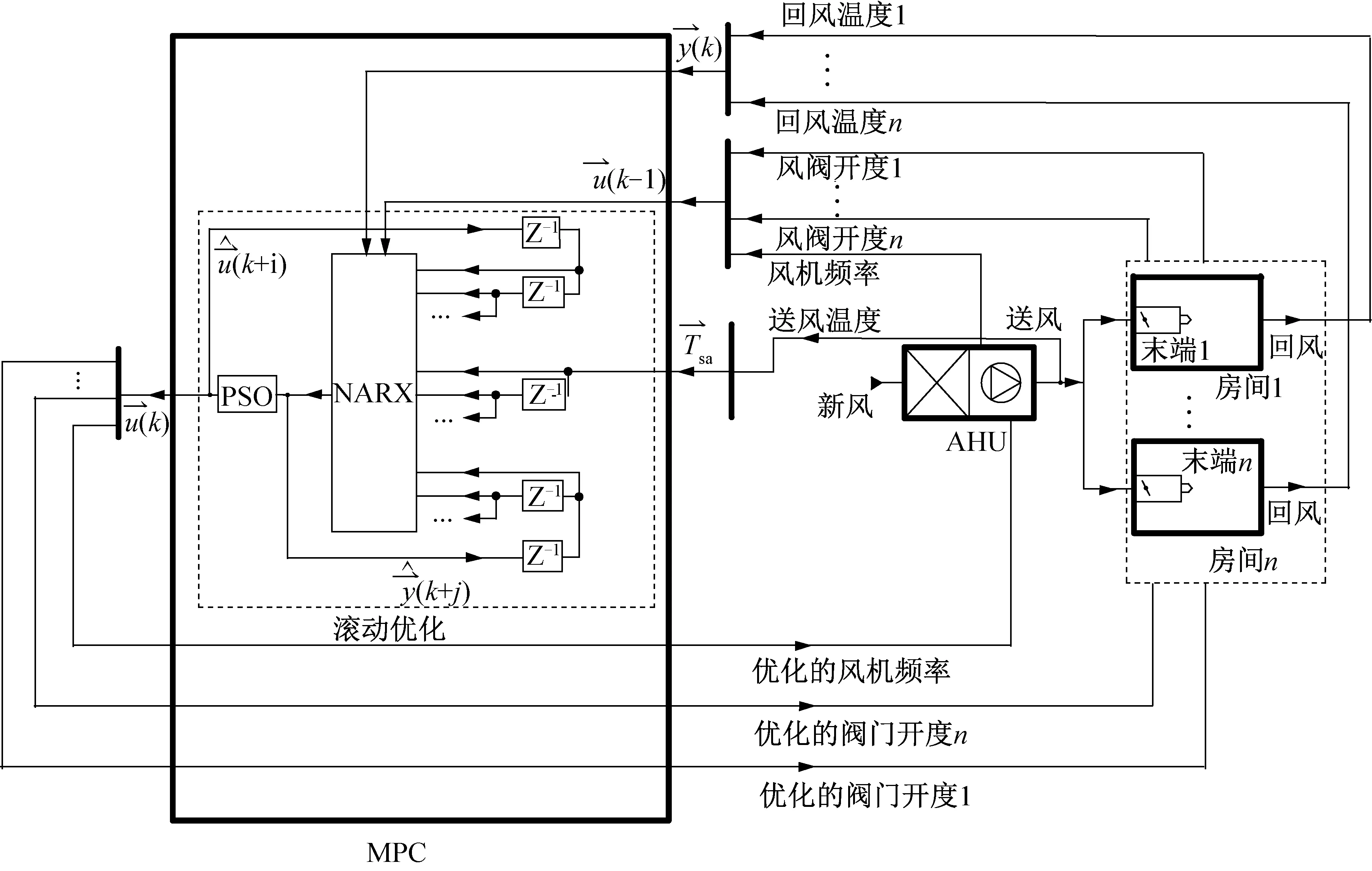
图4 基于MPC的VAV系统

寻求最优解需用到PSO优化算法，流程图如图3所示。在执行算法之前，应限定搜索域。本文VAV系统中，粒子位置矢量的元素包括风机频率和风阀开度，其中风机频率的搜索范围为20～50 Hz，风阀开度的搜索范围为0～100%。

图3 PSO方法流程图

本文研究了两种不同权值的方案，如表1所示。方案1强调控制精度，方案2同时考虑热舒适性和节能。值得注意的是，权值可以根据需求自行调节。考虑精度的情况下，应该尽量增大w1的权重；考虑节能的情况下，应增大w2和w3的权重。

图4所示为完整的基于MPC的VAV系统控制过程。

表1 两种权值的分配方案描述

对于惯性较大，受干扰后输出变化缓慢的系统，过小的预测域会导致控制器性能下降，但更长的预测域会增加计算时间而对控制效果没有好处。相反，对于反应迅速的系统，预测域应尽量小[19]。由于本文所用的实验系统热惯性较小(对阶跃扰量的稳定时间约为1 min)，故选择5 min的采样时间步长；预测域和控制域均选择5个采样步长，即25 min。上述设置在SIMULINK所建系统中得到了验证，能够实现好的控制效果，故在实验中，也将采用上述设置来配置MPC。

3 结果与讨论

基于NARX和PSO的MPC在实际制冷工况下的VAV系统中进行了验证，并与基于PI控制器的定静压控制方法进行了对比。

节选了3个房间NARX的验证结果如图5所示，结果以均方差(MSE, mean square error)来评定。MSE可表示为式(4)。训练和验证结果均方差分别为：房间#1：4.49×10-3和1.11×10-2；房间#2：5.33×10-3和9.57×10-3；房间#3：4.23×10-3和1.26×10-2。

(4)

式中：A为样本容量；Xtarget,a为实际值；XNARX,a为由NARX的输出值。

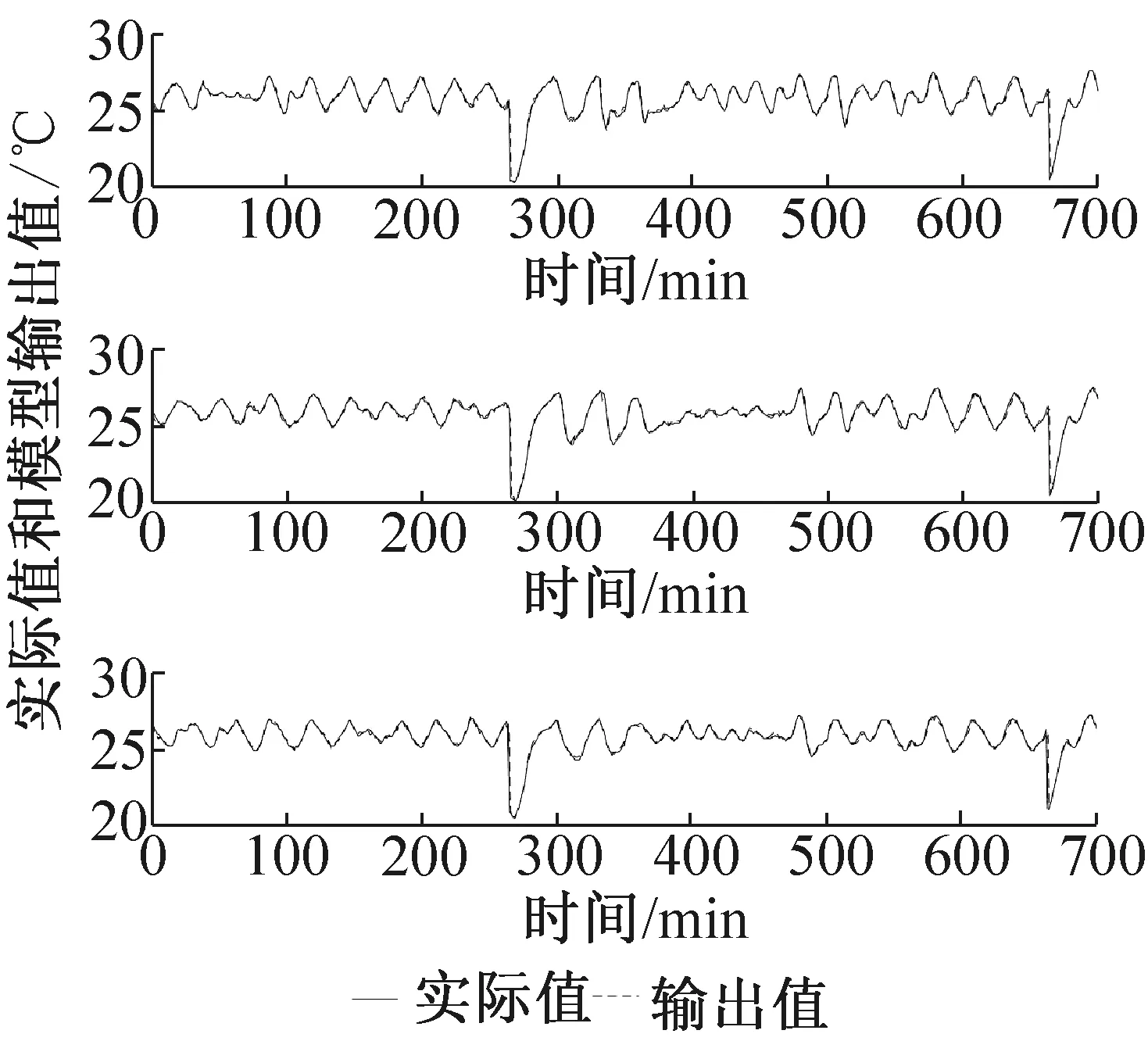
图5 NARX神经网络的验证结果

实验中，所有房间的设定温度保持25 ℃不变。不同控制模式下，即MPC方案1、MPC方案2和定静压模式，送风温度扰量如图6所示。同时，房间内还有一类扰量来自加热器，分别是：房间#1的电加热风机和房间#3的油汀。房间#1的电加热风机在实验开始后的第80 min，由低加热档位调为高加热档位；房间#3的油汀在实验开始后的第120 min，也由低加热档位调为高加热档位。

图6 送风温度和加热器扰量

为了克服扰量对房间温度的影响，MPC方案1、MPC方案2和定静压模式被执行。图7和图8所示为执行不同算法得到的控制变量，包括风机频率和各房间的阀门开度。由图7可知，在MPC的两种方案中，相较于定静压控制，风机频率对大扰量的响应更加迅速。如在扰量1出现时，MPC方案仅用一个控制时间步长(5 min)就做出了反应，而基于PI的定静压方法需要4个时间步长(20 min)。采用MPC方案2时，风机的频率也始终保持最小，这将大大节省风机能耗。由图8可知，采用MPC方案2时，3个房间的阀门开度大部分时间均为最大，此方案意味着风阀处的更小静压损失和噪音。

图7 不同控制方案下的风机频率优化值

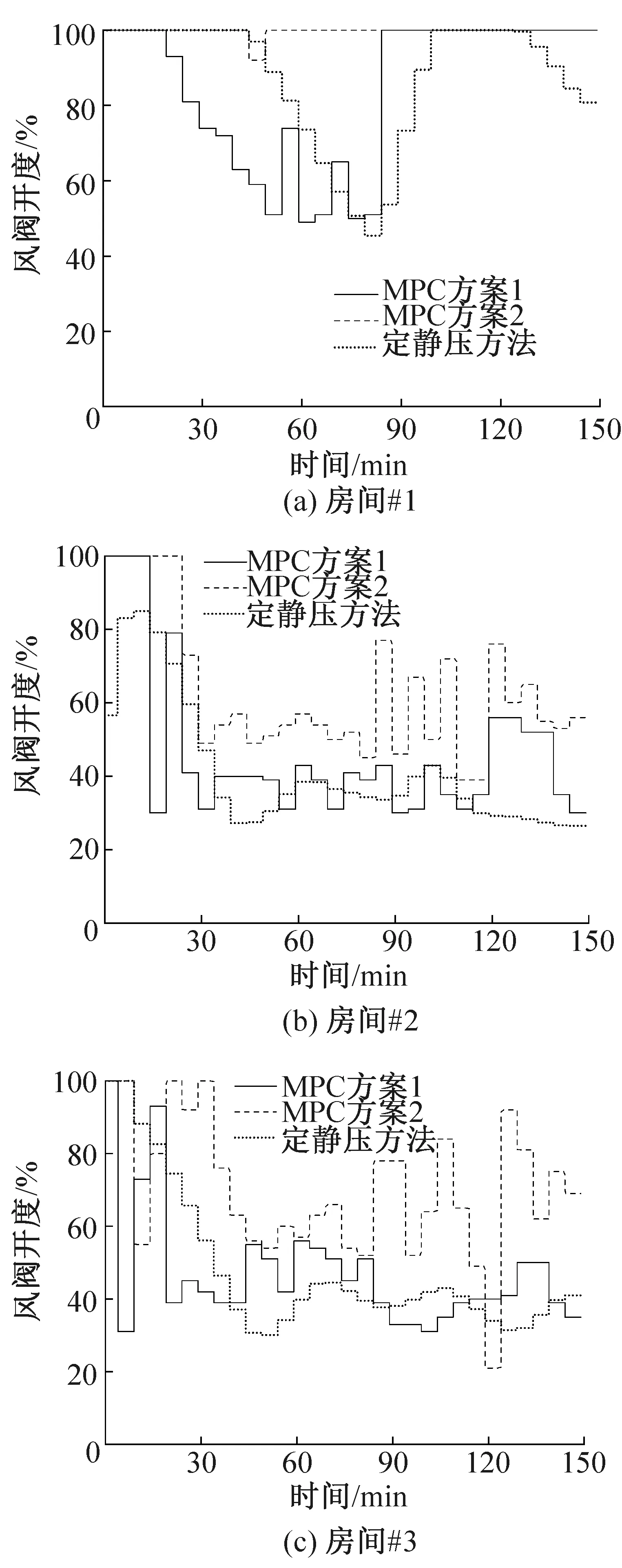
图8 不同控制方案下所有房间风阀开度的优化值

图9所示为3种控制方案的房间温度控制效果。MPC方案1可以实现最高的控制精度，其次是定静压控制方案和MPC方案2。特别是对于大扰动的情况，与其他两种控制方案相比，MPC方案1在控制精度方面具有明显优势。通过使用MPC方案1，室温偏离设定点可以稳定在±0.5 ℃之内，这远小于另外两种方案。特别是图9(b)和(c)中，房间#2和房间#3的室温在执行MPC方案2(节能算法)时，反而略低于设定温度。在扰量到来之前(即80 min之前)，房间温度达到稳定时，房间的总负荷小于AHU的最小制冷量，此时为了保持热舒适性，需减小风阀开度。MPC方案2为了减小静压损失，适当增加了房间#2和#3的风阀开度，如图8(b)和(c)所示，从而使房间温度降至设定点以下；而如图9(a)所示，房间#1的热负荷稍大于房间#2和房间#3，在阀门全开的情况下，恰好室温接近设定值。在扰量到来之后(即80 min之后)，因为一台风机同时给3个房间供风，为了满足房间#1的负荷需求，需要风机提供足够的风量并且保持房间#1风阀的最大开度，但这也导致房间#2和房间#3的冷量大量过剩。此时如果减小房间#2和房间#3的风阀开度，可使房间温度更接近设定温度，但会增加静压损失，增大能耗。因此房间#2和房间#3的风阀尽量保持了大的开度，以减小静压损失和噪音，室温也随之降至设定值以下。总体而言，MPC方案2要同时满足在所有房间的热舒适性和节能要求，必然会导致控制精度下降。

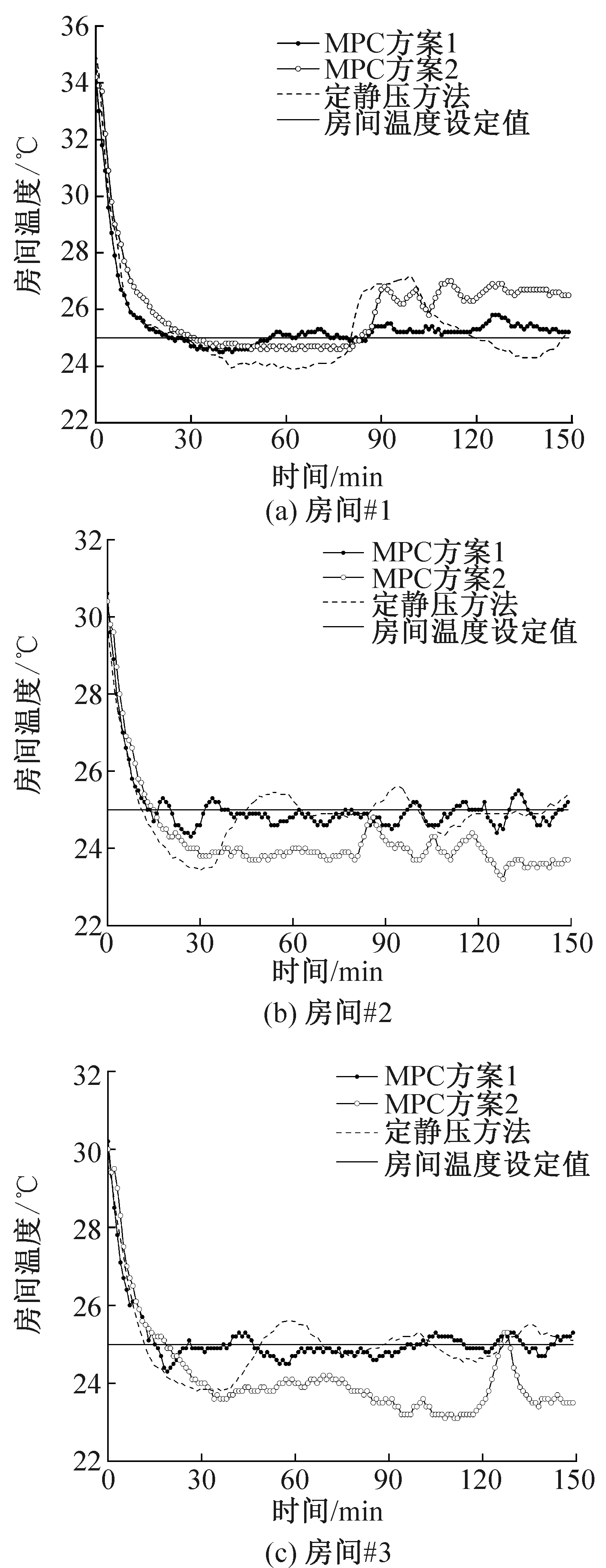
图9 不同控制方案下所有的房间温度值

通过使用3个指标，即室温的均方误差(MSE)(类似式(4))、能量消耗和阀门平均开度，可更具体地评估不同控制方案的控制性能。表2所示为3种控制方案的控制效果对比，使用MPC方案1可以实现室温的最低MSE(即最高控制精度)，但其消耗了最多的能量。MPC方案2的能耗最小，且可实现阀门的最大开度(这意味着更少的噪声和静压损失)，但其控制精度最低。总体而言，MPC方案1更适合于工业空调系统的应用，而MPC方案2更适合于建筑和商用空调系统的应用。

4 结论

本文提出的基于NARX的非线性MPC控制模型可实现VAV系统中的温度高精度控制或在保证热舒适性的前提下的节能控制，其主要贡献概述如下：

1) 对整个AHU风测系统进行建模，将优化变量选为模型的输入变量，减少需要测量的中间参数，如静压、风量、风速等，以此减少传感器的布置，大大节省了系统的建造成本，且能同时得到所有控制区域的优化控制输入，消除了所有的反馈滞后。

表2 3种控制方案的控制效果对比

2) 为成本函数的对象设置不同的权值，以此来切换MPC控制器的功能，包括精准模式和节能模式。精准模式最大程度的减小温度偏差；节能模式在保证热舒适性的前提下，相对于传统的定静压控制方法，能耗更低。

3) MPC控制器采用NRAX和PSO的组合，既保证了模型的精度，又减轻了上位机的计算负担。