指向式旋转导向系统内外环转速对PDC钻头破岩效率的影响

张光伟， 高嗣土， 乔 阳， 田 帆

（西安石油大学机械工程学院，陕西西安 710065）

近年来，国内外研制出多种形式的旋转导向钻井工具，其与PDC钻头配合可以显著提高硬地层的钻速[1-3]。为了进一步提高硬地层的钻进效率，人们开展了大量理论与试验研究[4-8]，但多集中于复合钻进条件下PDC钻头破岩效率研究，对旋转导向钻井条件下PDC钻头破岩效率的研究则较少。有人利用Matlab软件建立数字化PDC钻头和数字化岩石模型，模拟了复合钻进条件下岩石的破碎过程，并将模拟结果与试验数据进行了对比，发现两者吻合良好[9-10]。笔者借鉴前人的研究思路，以指向式旋转导向钻井工具可控弯接头为研究对象，利用Matlab软件对岩石进行离散化处理，研制了数字化导向钻进破岩仿真程序，给出了钻头切削岩石效率的表示方法，分析了可控弯接头导向机构中内外偏心环转速对PDC钻头破岩效率的影响，以期对提高指向式旋转导向系统的钻井效率有一定的指导作用。

1 PDC钻头的数字化模型

1.1 切削齿工作面的数字化

采用直角坐标系下的矩形等弧划分数字化方法建立PDC钻头齿工作面的数字化模型[11-12]，其数学表达式为：

式中：xp，yp和为切削齿工作面数字化节点p的坐标；R为PDC钻头切削齿的半径，mm；θstep为切削齿的角度步长，（°）；。

切削齿工作面数字化方法及模型如图1所示。

图1 切削齿工作面数字化方法及模型Fig. 1 Digitization method and model of cutting tooth surface

1.2 切削齿侧面的数字化

PDC钻头主切削齿的侧面为圆柱面，为了得到其数字化模型，将其在周向及轴线方向等分，设某数字化节点m的坐标为 (xm,ym,zm)，则：

式中：lstep为轴线方向上的长度步长l为切削齿圆柱部分长度，mm。

切削齿侧面数字化方法及模型如图2所示。

图2 切削齿侧面数字化方法及模型Fig. 2 Digitization method and model of cutting tooth side

1.3 规径齿的数字化

规径齿一般是由常规切削齿经过线切割加工获得的，如图3（a）所示。由于A点所代表的齿侧节点微元与钻头中心点O之间的距离大于钻头半径，属于被切割部分。在获得规径齿时，将A点向沿 PDC切削齿工作平面平行的方向，投影到大圆柱面即钻头外圆柱轮廓面，得到A′点，坐标为。设A点在Oxy平面内的坐标为，则：

规径齿数字化模型如图3（b）所示。

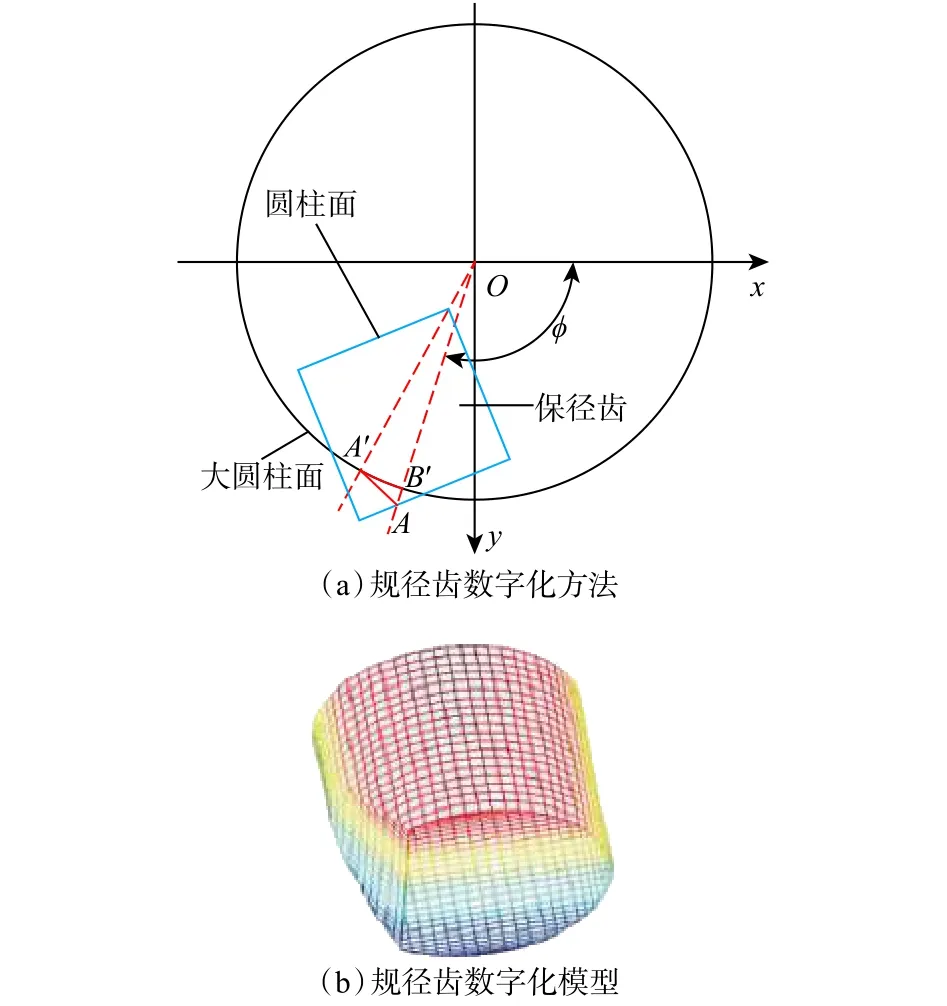
图3 规径齿数字化方法及模型Fig. 3 Digitization method and model of gauge teeth

至此，PDC钻头主要特征的数字化就已完成，根据每颗切削齿在钻头坐标系中的位置和方向参数，利用PDC钻头几何学基本方程[13]，基于Matlab平台进行矩阵的平移、旋转操作，即可绘制出由24颗规径齿构成的PDC钻头数字化模型，如图4所示。

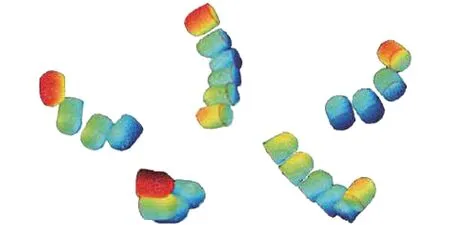
图4 PDC钻头的数字化模型Fig. 4 Digital model of PDC bit

2 岩石的数字化模型

将岩石抽象为由小立方体微元组成的离散化对象，微元的每个顶点为一个数字化节点，假设岩石为长方体岩样，以岩石上表面的形心为原点O，沿钻头垂直向下钻进的方向为Z轴，建立直角坐标系OXYZ，如图5（a）所示。设岩样的长宽高分别为l，w和h，则岩石上任意节点P有：

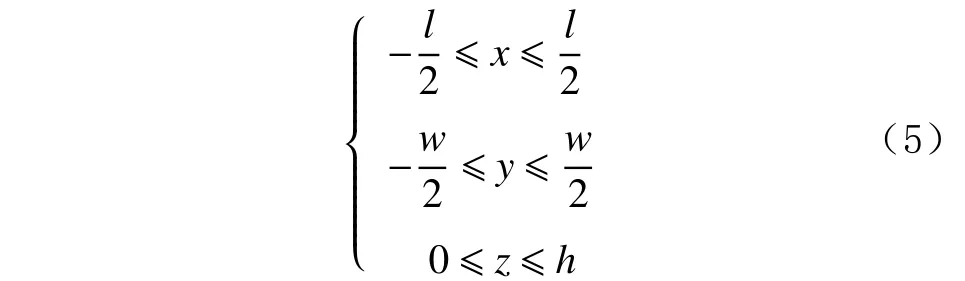
岩石的三维数字化模型如图5（b）所示。

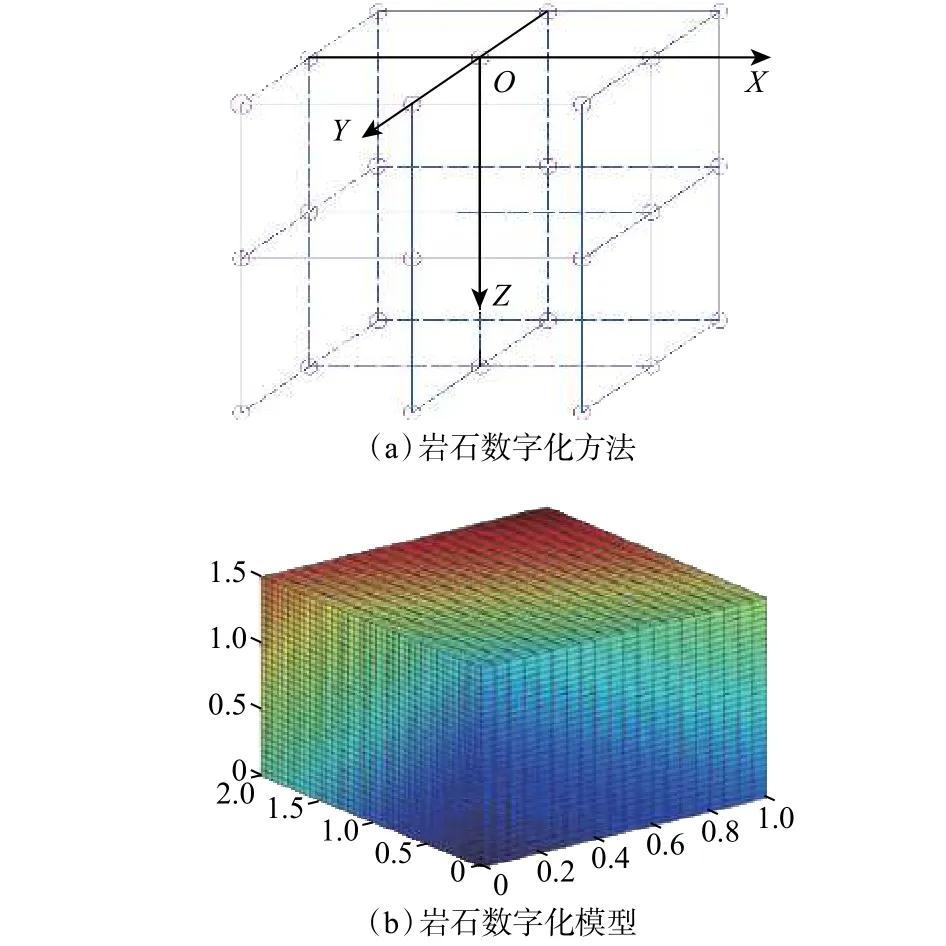
图5 岩石数字化方法及模型Fig. 5 Digitization method and model of rock

PDC钻头与岩石相互作用的实质是切削齿与岩石数字化节点的相互作用。因此，对岩石三维区域内的数字化节点赋予不同的抗剪强度、研磨性等物性参数，即可表示不同材质的数字化岩石。

3 PDC钻头破岩过程的模拟

将PDC钻头所有的数字化节点存放于Matlab矩阵中，按所需要的方式进行平移、旋转操作[14-15]。在旋转导向钻井条件下，将PDC钻头移至岩石表面、使钻头轴线与岩石Z轴重合，定义钻头沿自身轴线旋转，沿岩石Z轴竖直向下钻进，即可模拟钻头与岩石的作用过程。齿面节点与岩石的相互作用关系如图6所示。

设外部切削齿刃上某节点P在t时刻的坐标为Pt，在t-1时刻坐标为，由于模拟过程中每个时间步长钻头转过的角度和进尺都远小于钻头半径，故可认为节点P在t时刻的速度方向矢量为；同时，P点在t时刻周围有8个岩石数字化节点，这8个节点构成一个岩石正方体微元，通过对速度矢量向上和向下圆整，可得到Pt点在所处岩石微元的指向点Pf的坐标。

图6 齿面节点与岩石的相互作用关系Fig. 6 Interaction between tooth surface nodes and rock

经圆整处理后可获得t时刻P点在三维岩石上的“指向点”和“经过点”，其中“经过点”为被去除的岩石节点，去除“经过点”后，将Pt点的坐标值赋给Pf，就得到t时刻井底与井壁的坐标，将其进行三角剖分、曲面重构即可得到模拟井底与井壁的可视化模型。同理，齿面节点经过相应的圆整处理，如果能在岩石上找到其对应的“指向点”，则判定该节点与岩石接触，即可为计算切削齿接触面积做准备。

4 内外偏心环转速比对破岩效率的影响

4.1 破岩效率的定量表示

破岩效率可用岩石切削量定量表示，相同时间步长的切削量越大，意味着其破岩效率越高。切削量包括切削面积和切削体积，切削齿的工作区域由齿面工作区域与齿刃工作区域组成，如图7所示。

图7 齿刃与齿面工作区域Fig. 7 Tooth blade working area and tooth surface working area

数字化过程中，齿面和齿刃节点均匀分布，设切削齿工作面由N个数字节点组成，切削齿工作区域内包含n个节点，设第j个节点的坐标为），则齿面接触区域的形心H的坐标为：

在PDC切削齿齿刃上，采用齿刃等效接触点M来代替齿刃接触点进行切削参数的计算与分析，点M为齿面中心点C与齿面工作区域等效点H的连线与齿刃的交点，其坐标为：

式中：RH为H点到C点的距离，m。

根据接触面区域节点占齿工作面节点的比例，可得接触面积S为：

切削面积是接触面在过齿面定位点钻头轴线平面上投影的面积。由此，假设t时刻齿面中心点坐面法向量为。钻头与岩石互作用的过程中，由于钻头每步转过的角度步长很小，可近似认与齿面中心点在t时刻的速度方向一致，即为该时刻过C点钻头轴线平面的法向量。向量与向量n夹角的余弦为：

切削面积Sst为：

切削体积为t到t+1时间步之间的切削面积与齿面中心点行程的乘积，则在T时间步内，单切削齿的切削体积

4.2 导向轴指向角的确定

井下闭环可控弯接头是指向式旋转导向钻井系统的重要组成部分，由旋转外套、导向轴、导向机构、驱动电机和电子控制系统组成，如图8所示。可控弯接头导向机构为导向钻井工具的核心，主要由内、外偏心环组成，导向轴的一端由可控弯接头导向机构控制，另一端安装钻头[16]。

图8 可控弯接头的结构Fig. 8 Structure of the controllable bending joint1.外偏心环驱动电机；2.外偏心环连接法兰；3.外偏心环； 4.内偏心环；5.内偏心环连接法兰；6.内偏心环驱动电机；7.导向轴；8.扭矩传递机构；9.密封结构；10.球座；11.旋转外套

钻井过程中，井下闭环可控弯接头通过调整旋转外套、外偏心环和内偏心环的相对位置，可以改变导向轴的空间姿态，实现可控弯接头工具角和工具面角的调整，从而实现定向钻进，可控弯接头导向机构的运动简化模型如图9所示。设内偏心环的角速度为ω1，几何中心为E；外偏心环的角速度为ω2，几何中心为E1；偏心环组的几何中心为E2，旋转外套的角速度为ω3，用2个向量代替内、外偏心环的偏心距e。

图9 导向机构运动模型简化示意Fig. 9 Schematic diagram of the movement model of the steering mechanism

根据导向机构运动简化模型的几何关系建立数学方程，可得偏心环组中心点E2与可控弯接头导向轴线的夹角φ′为：

考虑旋转外套的旋转，其夹角变为：

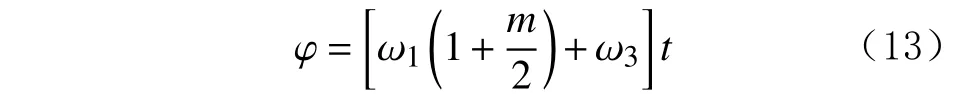
式中：m为内外偏心环的转速比；t为时间步长。

钻进过程中，井下闭环可控弯接头指向角为钻头中心线与钻井工具轴线的夹角。因此，理想状况下，一定时间步长内的可控弯接头指向角只与内、外偏心环的转速比有关。

4.3 内外偏心环转速比对切削量的影响

对于可控弯接头，影响切削量的主要因素为可控弯接头导向轴的指向角和旋转外套的长度L，因为它们决定了钻头中心与井眼中心的偏心距。由于旋转外套的长度是固定的，所以内、外偏心环转速比对可控弯接头的破岩效率起着主导作用。

导向钻进过程中，井下闭环可控弯接头带动钻头在井底旋转一周，钻头上的每个切削齿都经过井眼参考垂直平面，各切削齿的切削面积为各齿切削轨迹和前一次作用的叠加区域，不利于计算，笔者选用距离井眼中心40 mm的外部单齿为研究对象，切削齿半径R为16.0 mm，齿的前倾角为12°，进齿深度为2.0 mm，模拟钻进总深度为16.0 mm（2个钻井循环），整个过程需要756时间步，定义可控弯接头与转盘的转速比为3∶1，旋转外套的长度L为1 000 mm，岩石的抗剪强度为11 MPa，内摩擦角为22°，摩擦系数为0.2，然后进行模拟计算。

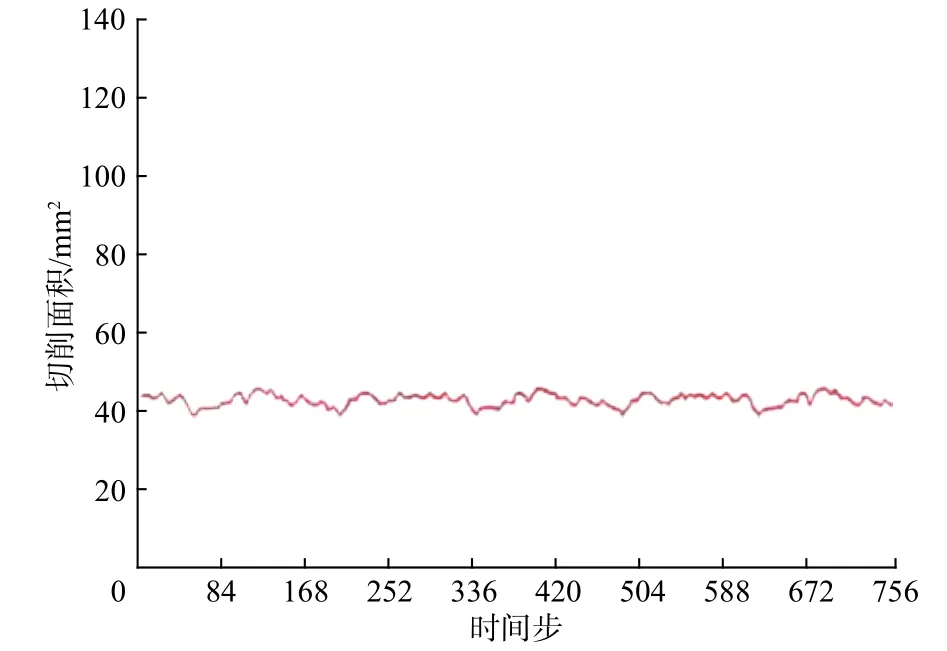
图10 外部单齿在时的切削面积Fig. 10 Cutting( area o)f external single teeth at the time

图11 外部单齿在m=0.5时的切削面积Fig. 11 Cutting area of external single teeth at m=0.5

图12 外部单齿在m=1.0时的切削面积Fig. 12 Cutting area of external single teeth at m=1.0

图13所示为不同转速比下切削体积随时间步长的变化曲线。从图13可以看出：可控弯接头中的内外偏心环转速比由0逐渐增大到0.8左右过程中，其切削体积呈线性增加，这是因为内外偏心环转速比增大，导向轴指向角增大，岩屑积累量增大，此时岩屑随着钻头共同作用，导致破岩接触面积显著增大，破岩效率明显增大。若持续增大内外偏心环转速比，则岩屑积累厚度增加导致钻头切削深度减小，再加上钻井工具自身造斜条件的限制，其切削体积趋于恒定。

5 结 论

1）基于Matlab软件建立了一种模拟旋转导向钻井模式下PDC钻头钻进的方法，模拟了旋转导向钻井条件下数字化PDC钻头与数字化岩石的相互作用过程，给出了破岩效率的定量表示方法，为研究提高旋转导向钻具破岩效率提供了思路。

图13 外部单齿在不同转速比下的切削体积Fig. 13 Cutting volumes of the external single tooth at different speed ratios

3）PDC钻头外部切削齿的切削体积随着转速比增大发生相应变化，切削体积在初始阶段近似呈线性增加；转速比达到0.9左右时，切削体积增大速度趋于平缓，最终达到平衡状态。

4）模拟结果表明，对于抗剪强度为11 MPa、内摩擦角为22°、摩擦系数为0.2的岩石，最佳破岩转速比在1.0左右；岩石切削量最大的时间步长区间为 300～450。