基于声波时差数据波动性识别异常压实地层的方法

2019-12-28席鹏飞杨明合郭王恒石建刚

石油钻探技术 2019年6期

席鹏飞，杨明合，郭王恒，石建刚

（1. 中国石油钻井工程重点实验室长江大学研究室，湖北武汉 434000；2. 中国石油新疆油田分公司工程技术研究院，新疆克拉玛依 834000）

声波时差法是计算异常压实地层压力的一种常用方法，其核心是在确定正常压实段声波时差趋势线基础上，准确计算异常声波时差点偏离趋势线的程度[1-3]。由于声波时差受地层岩性等因素的影响会出现波动，影响了利用声波时差识别异常压实地层的精度。现场往往是结合实钻及测井等资料识别异常压实地层、计算异常压实地层的压力。该方法的识别精度取决于个人的经验及对地层的认识程度，不可避免地存在随意性和盲目性，因而异常压实地层的识别精度不高。为提高识别异常压实地层的精度、准确预测异常压实地层的压力，除需要对声波时差数据进行预处理外，还要进一步研究声波时差数据自身包含的规律。为此，笔者采用密度聚类法来剔除声波时差数据中的无效数据，基于小波理论分析了正常压实段内声波时差沿正常压实趋势线的波动性[4-6]。通过分布拟合检验，确定了声波时差波动性的概率分布函数，从概率的角度辨识异常压实地层，避免了实际计算中的随意性，该方法同样适用于其他类似测井资料（如密度）的分析。

1 正常压实段声波时差数据的分布拟合

对于正常压实地层，井深与声波时差的自然对数呈线性关系[7]：

1.1 剔除无效数据点

由于受地层、井径和测量仪器等因素的影响，声波时差数据中含有较多无效数据，笔者采用密度聚类（dbscan）法对声波时差数据进行预处理[8-9]。图1为新疆油田玛湖凹陷A井501.00～4 190.00 m井段21 297个声波时差数据聚类分析结果，图中580个噪声点和769个边界点为无效数据，其余为核心点，聚为2簇。初步判断第1簇核心点位于正常压实地层，对应508.00～2 965.00 m井段。

图1 A井声波时差数据密度聚类分析结果Fig. 1 The results of density clustering analysis by interval transit time in Well A

1.2 正常压实段声波时差数据的波动性分析

图2 所示为图1中正常压实井段（第1簇核心点）的散点图。从图2可以看出，该井段声波时差的自然对数与井深明显呈线性关系，拟合关系式为：

Fig. 2 The distribution of lnΔt along well depth at normally compacted section

由图2可知，随井深H增大，在趋势线两侧波动显著，显然受地层因素影响较大。这种波动可用小波分析进行描述[10-11]。依据小波分析理论，数据点沿其趋势线方向的波动可用如下公式描述：

实际上，若设低频信号为直线，可利用点到直线的距离公式，直接导出式（3）。对于图2中的任意一点，若其位于趋势线上方，则该点到趋势线的距离为：

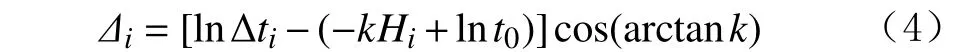
当趋势线斜率k很小时，，则式（4）可改写为：

若点i位于趋势线下方，则该点到趋势线的距离为。

图3 正常压实段波动项沿井深的分布Fig. 3 Distribution of fluctuation item along the depth of well at normally compacted section

图4 波动项分布的拟合Fig. 4 The fitting of the fluctuation item distribution

1.3 正常压实段声波时差数据频率分布

tLS分布和LG分布的概率密度函数分别为：

式中：Γ（x）为伽马函数；μ为位置参数；σ为尺度参数；ν为形状参数。

在Matlab软件的Distribution Fitting模块中，分别用tLS分布和LG分布的概率密度函数拟合波动项的分布规律，结果见图4。由图4可知，相较于正态分布，tLS分布和LG分布更加接近波动项的分布频率。拟合确定的tLS分布和LG分布概率密度函数的参数值见表1。

表 1 tLS分布和LG分布概率密度函数的参数Table 1 Probability density function of the tLS distribution and the LG distribution

1.4 波动项Δ频率分布的拟合检验

分布拟合检验基于假设检验，通过检验给定分布函数与样本分布的符合程度，从而对该分布做出取舍[14]。数据点数n大于2 000时，常用皮尔逊卡方（χ2）和柯尔莫哥洛夫-斯米诺夫（K-S）检验[15-16]，笔者采用χ2进行拟合检验。

皮尔逊检验统计量χ2为：

式中：n为试验次数；k为样本空间划分的子集（或区间）的个数；pi为第i个子集上给定分布的概率；fi为第i个子集上样本出现的频数。

一般当总体分布未知时，检验假设H01：总体分布函数为 tLS，即X～F(μ，σ，v)；H02：总体分布函数为 LG，即X～L(μ，σ)。

当试验次数n充分大（n=13 099≥50），则当H0为真时，统计量χ2近似服从自由度为k-1的χ2分布[16]，故在给定显著性α的条件下，H0的拒绝域为：

图5 k=50时2种分布与样本的频率拟合Fig. 5 Frequency fitting of two kinds of distributions and samples when k=50

从图5可以看出，第i个区间上tLS分布和LG分布的值在区间中心区域小、边缘大。进一步分析发现，在边缘区间内，波动项的频数fi都很小（＜50），相对样本总量可以忽略，在计算χ2时需忽略这些将导致χ2明显增大的边缘区间，即有效样本区间为11～41区间。

当显著性水平α=0.05时，根据式（8）计算出tLS分布的χ2=51.1，而(50-1)=66.339，不满足式（9），接受H01，认为波动项Δ的分布符合tLS分布。同理，计算出LG分布的χ2=84.9，满足式（9），则拒绝H02，即认为波动项Δ的分布不符合LG分布。

2 异常压实段概率分析

对于第i点声波时差，越大，与位置参数μ的距离越大，也就是到“由式（1）确定趋势线”的距离就越大，即属于正常压实段的可能性越小。据此可以构建属于正常压实段概率的计算公式。从tLS概率密度函数图（见图6）可以看出，对于任意，可以用图中阴影面积S来表示距离μ的远近程度。结合概率定义，那么属于正常压实段的概率pi可表示为：

式中：f(x)、P(x)和F(x)为tLS分布的概率密度函数、概率函数和概率分布函数，其参数可从上文求出。

图6 正常压实段波动项Δi的tLS分布Fig. 6 tLS distribution of fluctuation item Δi at normally compacted section

图7 A井lnΔt及pi沿井深的分布Fig. 7 Distributions of lnΔt and pi along well depth in Well A

从图7可以看出：500.00～2 950.00 m井段绝大部分pi大于0.12，位于3σ直线上方。若以3σ作为判断标准，则该段属于正常压实段；井深2 950.00 m以深井段的pi小于0.02，属于正常压实段的概率基本为0，为异常压实段。实钻资料显示，该井在井深2 940.00 m左右压力明显抬升，地层压力系数由1.04升至1.71，证明该方法识别异常压实段的可靠性较好。