高水头水工隧洞钢筋混凝土衬砌承载特性分析

2019-12-27朱奎旭陈俊涛王安亭

中国农村水利水电 2019年12期

朱奎旭，肖明，陈俊涛，王安亭

(1. 武汉大学水资源与水电工程科学国家重点实验室，武汉 430072；2. 武汉大学水工岩石力学教育部重点实验室，武汉 430072)

0 引言

圆形有压水工隧洞运行时钢筋混凝土衬砌受内水压力的作用，其环向应力一般表现为拉应力，在高水头的作用下，混凝土容易超出其抗拉强度产生裂缝进而导致内水外渗。目前，针对高水头的水工隧洞一般采用透水衬砌的设计原则，认为承担较大内水压力的钢筋混凝土衬砌必然会开裂，内部的高压水通过裂缝进入围岩，使得隧洞外的渗透压增大，进而对隧洞自身和围岩的稳定产生影响[1-3]。因此合理模拟水工隧洞衬砌承载过程中的损伤开裂行为，对地下钢筋混凝土衬砌管道设计和水工隧洞区域围岩稳定校核具有重要意义。

针对透水衬砌的设计原则，我国《水工混凝土结构设计规范》(SL 191-2008)和《水工隧洞设计规范》(SL 279-2016)基于大量的实验数据给出了裂缝宽度计算的近似公式，但公式具有较强的工程依赖性。潘家铮[4]提出了以围岩和内水压力为主要影响因素的裂缝计算方式，但该公式未考虑钢筋对裂缝的限制作用；刘秀珍[5]基于有限元的思想，将钢筋混凝土衬砌看成是弹性地基上的曲梁结构，但其假定围岩不发生开裂，切向抗力沿接触面均匀分布。针对透水衬砌的数值模拟，肖明等[6]基于弹塑性损伤有限元，提出了衬砌裂缝宽度的估算公式；苏凯等[7]基于渗透水压力以体力方式施加的原则，提出了围岩和衬砌联合承载的耦合分析方法。高水头水工隧洞衬砌开裂不可避免，开裂后由于混凝土与钢筋的变形不再保持协调，两者在接触面上势必会产生黏结滑移。目前有关水工隧洞衬砌黏结滑移行为的研究较少，相关实验表明黏结滑移行为对钢筋混凝土构件的承载能力、裂缝分布均有重要影响。因此本文基于前人的研究成果，为反应衬砌开裂阶段钢筋与混凝土黏结滑移行为的影响，在弹塑性损伤有限元计算中考虑黏结应力的作用，采用耦合计算方法研究内水压力增大过程中水工隧洞衬砌的受力损伤特征，并对损伤开裂前后渗流场及围岩破坏区的分布进行分析。

1 钢筋混凝土衬砌加载状态

由钢筋混凝土构件加载变形的特点，可将整个变形过程分为线弹性阶段、弹塑性损伤阶段、损伤开裂滑移阶段。相邻阶段的分界点为混凝土进入损伤演化过程、混凝土单元达到极限拉应变产生开裂。水工隧洞的实际监测数据表明，衬砌的钢筋应力一般低于其屈服强度，因此本文不考虑钢筋的塑性行为。

1.1 线弹性阶段

内水压力较低时，钢筋混凝土衬砌不会开裂，此时混凝土几乎不发生损伤，钢筋和混凝土处于弹性状态，应力应变呈线性关系。此时，根据有限元基本方程，由钢筋与混凝土之间的变形协调，可得到单元的弹性矩阵：

[H]e=[Hc]+[Hs]

(1)

式中：[Hc]为混凝土弹性刚度张量；[Hs]为钢筋弹性刚度张量。混凝土视为均匀各向同性材料，钢筋采用杆单元模型，相应的矩阵形式见文献[8]。

1.2 弹塑性损伤阶段

当混凝土单元进入塑性状态时，混凝土损伤开始，此时混凝土的本构关系采用考虑损伤的弹塑性材料增量形式[9]：

(2)

式中：D表示材料的损伤内变量；Hep为弹塑性矩阵[6]；δij为Kronecker Delta函数。单元刚度矩阵叠加形式与式(1)相同。

对于混凝土损伤，采用Mazars的混凝土拉伸试验拟合的演化方程来模拟[10]：

(3)

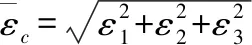
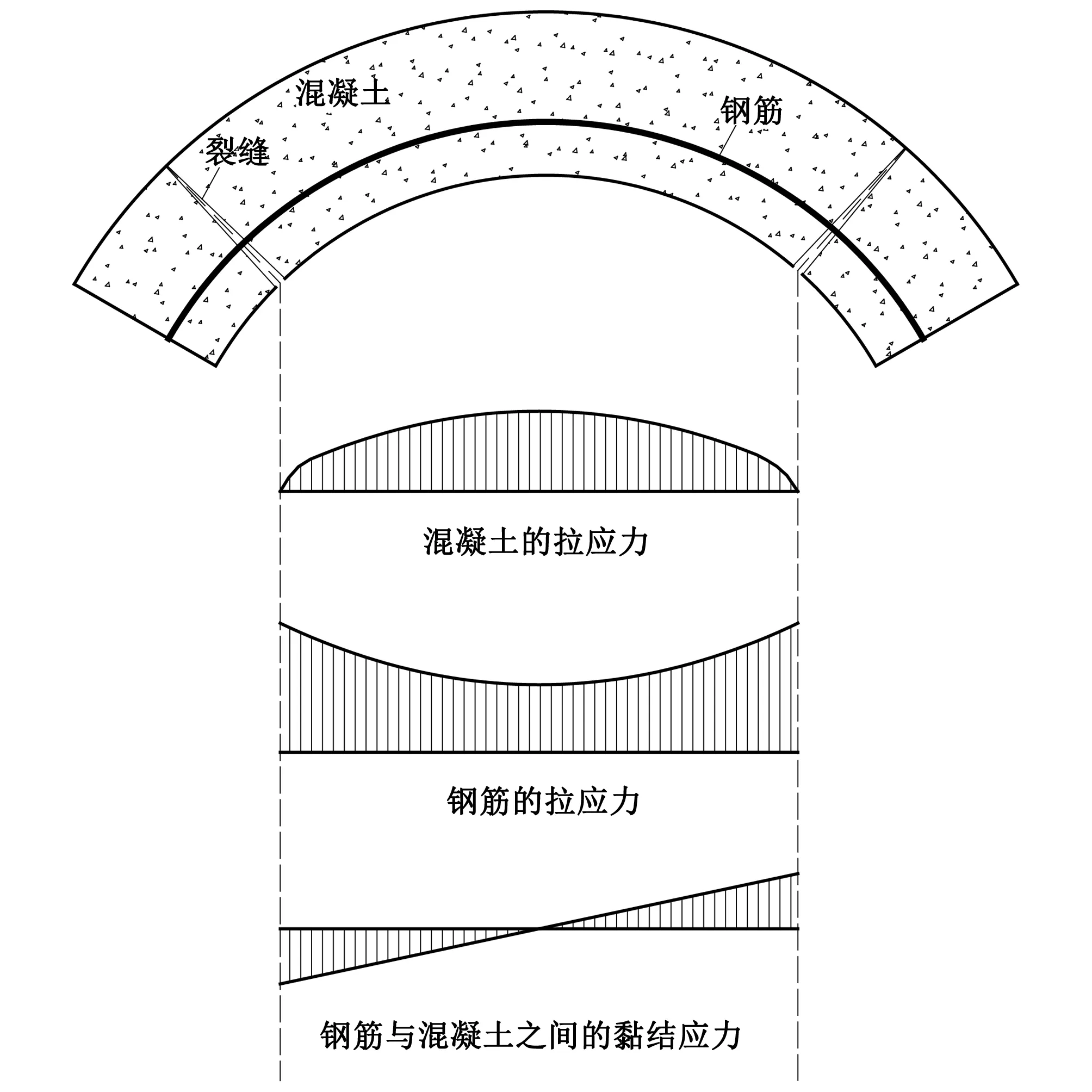
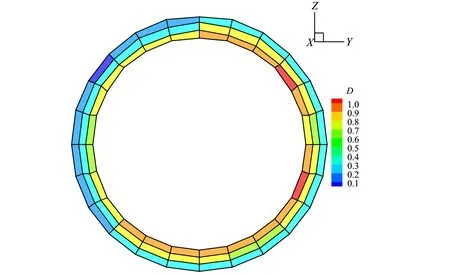
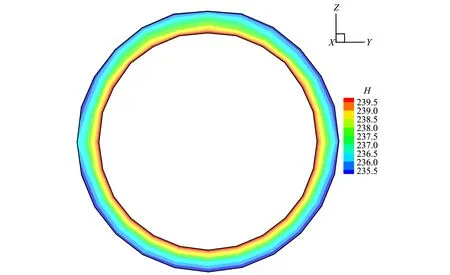
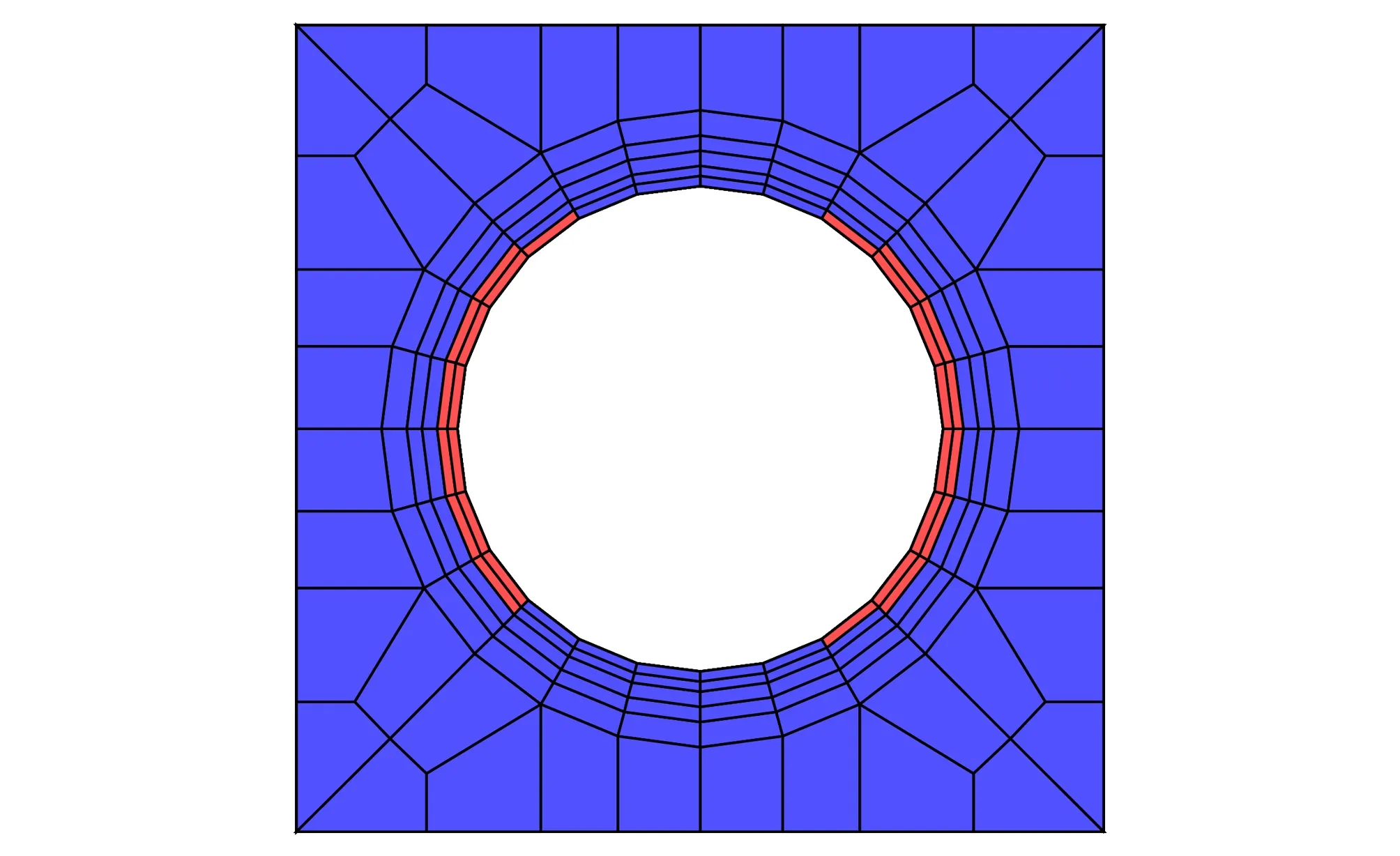
式中：At，Bt、为试验曲线拟合常数，对于一般混凝土0.7

1.3 损伤开裂滑移阶段

一般认为当混凝土单元达到极限拉应变或者计算所得的损伤量值达到0.90后，混凝土单元产生开裂[11]。假设衬砌开裂的发展方向垂直于单元最大主应变方向，沿此方向的混凝土刚度会逐渐降低，开裂的混凝土单元刚度矩阵应按照各向异性材料进行修正[12]，修正后的矩阵需转换为整体坐标系下的应力应变矩阵：

(4)

式中：βt为残余抗剪系数，描述开裂混凝土的残余抗剪能力；Ec、v分别为混凝土的弹性模量和泊松比。

工程监测数据表明，水工隧洞衬砌开裂后，钢筋应力在裂缝处达到最大值，在两个裂缝中间为最小值。钢筋应力大小沿纵向发生变化，其表面必然有相应的黏结应力分布，如图1所示。黏结应力的存在使得混凝土内的钢筋平均应变小于钢筋单独承载时的变形，被称为钢筋混凝土构件的受拉刚化效应[13]。刚化效应的存在导致衬砌开裂后裂缝间的单元刚度会得到提高，使得这部分单元更易处于弹塑性损伤阶段而不会产生开裂。

图1 实验拟合黏结应力模型Fig.1 Experimental fitting bond stress model

当水工隧洞衬砌形成径向裂缝时，裂缝处的黏结应力达到最大值，构件达到临界黏结状态，此时的黏结应力称为劈裂应力τcr，如图2所示，可由相应的经验公式求得[13]：

(5)

式中：ft为混凝土的抗拉强度设计值；c、d为水工隧洞的形状参数。

图2 水工隧洞劈裂应力示意图Fig.2 Schematic diagram of splitting stress in hydraulic tunnel

Schleiss A J等[14]通过实验数据拟合黏结应力量值在裂缝之间线性变化，在相邻裂缝中截面处为0，如图1所示。定义单元内钢筋与混凝土间的黏结应力为ητcr，其中η=0～1，在相邻裂缝中截面处取0，在含裂缝的单元处取1。

钢筋混凝土的黏结滑移本构模型一般定义为黏结应力与滑移量之间的关系[15]：

τ=14.9×103S-1.16×106S2-0.07×109S3

(6)

式中：τ为黏结应力量值；S为滑移量，即钢筋与混凝土接触面上的相对位移，图3为相应的τ-S曲线。

图3 黏结滑移曲线拟合模型Fig.3 Bond slip curve fitting model

根据衬砌单元内钢筋与混凝土之间的黏结应力ητcr求取相应的滑移量S，由于除裂缝所在单元外，其余单元黏结应力均未达到最大黏结应力，因此计算所得滑移量S唯一。单元内钢筋与混凝土的应变差值为Δε=S/L，L为衬砌单元内环向钢筋的长度。衬砌单元应力可用混凝土应变Δεc表示，如式(7)，有限元方程求解的未知量为衬砌单元内混凝土的位移值。

(7)

[R]=(cosα·cosβsinα·cosβsinβ0 0 0)T

(8)

式(7)右端第二项表示钢筋额外伸长对应的部分应力，可用初应力法计算其等效节点荷载代入有限元控制方程中，如式(9)所示。

{Fs}e=∭Ω[B]T[Hs][R]{Δε}dxdydz

(9)

式中：[B]为应变计算矩阵。

2 混凝土衬砌渗透损伤耦合计算

衬砌的渗透损伤耦合计算采用间接耦合的方式，渗流场通过渗透体积力影响结构的应力场，进而影响材料的损伤演化；结构的损伤开裂通过改变渗透系数从而对渗流场的分布产生影响。

2.1 渗流场与等效节点荷载的数值解法

对于各向异性的均匀介质，根据达西定律，可以导出稳定渗流场的微分方程：

(10)

式中：带下标的k为计算坐标下的渗透系数；Q为内源；H为水头。

对上式进行积分求和，得出三维有限元渗流方程：

[A]{H}={F}

(11)

式中：{H}为结点水头列向量；{F}为渗流边界积分得到的结点荷载；[A]为渗流有限元单元传导矩阵。

渗流场计算完成后，渗透荷载以体积力的形式作用于应力场，形成作用在模型节点上的等效荷载[16]：

(12)

式中：γ为水的重度；[N]为有限元插值形函数；H为结点水头；Ω为单元积分域。

2.2 损伤开裂与渗流的耦合关系

混凝土和围岩的力学特性及损伤破坏机制较相近，因此基于Louis[17]钻孔加压实验的渗透系数与正应力的经验公式，考虑损伤演化对渗透系数的影响，引入渗透突跳系数ξi描述混凝土应力损伤开裂对渗流的影响。表1为不同单元状态的渗透突跳系数ξi取值。考虑应力和损伤影响后的主应力方向渗透系数为：

k=ξik0ebσi

(13)

式中：k0为混凝土材料初始渗透系数；b为试验确定的耦合系数；σi为单元有效应力。

表1 不同单元状态下的渗透突跳系数Tab.1 Penetration mutation coefficients at different status

3 工程实例

3.1 工程概况和计算条件

某电站位于我国河南省境内，设计总装机规模1 000 MW，由上水库、下水库及输水发电三大系统组成。电站上下游水库间直线距离1.88 km，平均水头240 m。

计算模型包括引水隧洞的上游有压洞段、高压岔洞段以及下游有压洞段。本文主要针对上游有压洞段分析，开挖洞径为9.6 m，衬砌后过水洞径为8.0 m，衬砌厚度为0.8 m。模型坐标系为：坐标原点位于高压岔洞交叉中心；X轴沿洞轴线指向下游为正，范围-124.81～58.78 m；Y轴垂直于水流方向，范围-68.70～46.00 m；Z轴与大地坐标重合竖直向上为正，深度范围由-29.07～380.00 m。模型共剖分475 113 个8结点等参单元，其中衬砌单元13 464 个，开挖单元6 732 个。引水隧洞区域有限元模型如图4所示，引水隧洞钢筋混凝土衬砌的有限元模型如图5所示。模型中各项材料参数取值见表2。

图4 引水隧洞区域有限元模型Fig.4 Finite element model of the diversion tunnel area

图5 引水隧洞衬砌单元模型Fig.5 Model of the lining element of the diversion tunnel

表2 材料参数Tab.2 Parameters of materials

初始地应力场通过实测地应力反演获得，隧洞区域第一主应力在-5～-10 MPa范围内，属于偏低应力场。计算程序采用课题组自主开发的三维弹塑性损伤有限元程序，并在此基础上进行改进。对该有压管段进行以下计算：洞室在支护条件下进行开挖；隧洞充水运行，衬砌结构在渗流场的作用下损伤开裂。为了保证非线性问题的收敛，采用梯形分级加载[18]的形式施加内水荷载，迭代平衡以渗流场和应力场收敛为标志。

3.2 计算结果与分析

(1)衬砌受力损伤分析。当内水压力小于80 m时，钢筋和混凝土共同承担内水压力，二者协调变形，混凝土未出现损伤。随着内水压力增大至约165 m时，大部分混凝土进入塑性损伤状态，混凝土内部微裂隙扩展，衬砌渗透能力增强，进而对渗流场和应力场产生影响。当内水压力全部施加并迭代平衡后，由衬砌结构的损伤系数分布图6可知，衬砌单元损伤量值在腰拱部位达到最大，进入损伤开裂阶段，向顶部和底部逐渐减小，处于弹塑性损伤阶段。分析计算过程可知，由于隧洞所在区域反演得到的地应力场侧压力系数较大，在开挖过程中，隧洞开挖边界的围岩在腰拱两侧损伤最为严重，承载能力较低，从而导致在渗流-应力耦合计算中衬砌在该处受力状态更为不利，容易进入损伤开裂状态。

图6 衬砌结构损伤系数Fig.6 Damage coefficient distribution of lining

(2)渗流场计算结果分析。通过三维渗流场计算，可得当内水压力增大导致衬砌损伤开裂后渗流场的分布如图7所示。由于钢筋与混凝土的承载能力不同，在较大的拉力荷载作用下，衬砌混凝土单元不可避免的发生损伤及开裂，损伤状态下的混凝土由于内部的微裂隙扩展导致渗透系数显著增加，从而影响渗流场的分布。若假定衬砌渗透系数在计算过程中保持不变，计算得到的渗流场分布如图8所示。对比可以看出考虑

图7 损伤开裂阶段的衬砌压力水头等值线图(单位：m)Fig.7 Lining pressure head contour of damage cracking stage

图8 不考虑损伤的衬砌压力水头等值线图(单位：m)Fig.8 Lining pressure head contour without considering damage

损伤开裂后衬砌内的压力水头极差明显减小，相应的水力坡降有所减小。这表明考虑损伤开裂后，衬砌所承担的内水压力降低，部分内水压力由衬砌转为围岩承担，围岩内部的水力坡降增大。因此基于透水衬砌的设计原则，必须要注重围岩的防渗抗渗性能处理，防止由于内水外渗导致区域围岩产生渗透破坏。

(3)围岩破坏区分析。将渗流场计算得到的渗透结点荷载作用于围岩，得到考虑损伤开裂后围岩的破坏区分布如图9所示。图10是假定渗透系数不发生改变时的围岩破坏情况。可以看出，衬砌损伤开裂后，围岩破坏范围有所增加，尤其在衬砌损伤严重部位对应的围岩破坏体积明显增大。这说明基于透水衬砌的设计原则，围岩承担的内水压力比重增大，其受力状态更为不利，不考虑内水外渗的水工隧洞稳定计算偏于保守。

图9 损伤开裂阶段的围岩破坏区分布图Fig.9 Failure zones of surrounding rocks of damage cracking stage

图10 不考虑损伤的围岩破坏区分布图Fig.10 Failure zones of surrounding rocks without considering damage

(4)衬砌裂缝分析。迭代平衡时，渗流场的结点水头收敛，无渗透荷载增量，衬砌的平均损伤系数和等效渗透系数也达到定值。此时，根据损伤开裂单元的应力数值和钢筋的变形模量，可以近似计算出相应的衬砌裂缝宽度，考虑黏结滑移后的裂缝宽度约为0.153 mm，而不考虑黏结滑移效应时约为0.168 mm，表明考虑黏结滑移作用对减小构件的裂缝宽度有利，符合相应的物理实验规律。分别计算两种情况下混凝土的应变数值，考虑黏结滑移后混凝土的平均拉应变约为0.57×10-4，未考虑黏结滑移时混凝土平均拉应变约为0.69×10-4，可知黏结滑移提高了裂缝间的单元刚度，降低了裂缝间混凝土的平均拉应变，从而导致已有裂缝的钢筋混凝土构件更不易产生新的裂缝，这与水工隧洞裂缝少而宽的分布特征相符。