基于局部离散度的监督型线性判别分析及其应用
2019-12-27孙小丹
孙小丹,陈 文
(福州职业技术学院,福建福州 350108)
0 引言
相比高空间分辨率影像,多光谱/高光谱影像提供了更为丰富的光谱数据,因此,地物的光谱特征为此类影像分类一个重要依据[1-3].然而,在多光谱/高光谱影像的光谱数据中,相邻波段之间存在着大量信息冗余,使得影像数据结构呈高度的非线性,导致了随着光谱数据的增加非但不能有效地提高影像的分类精度,同时还降低了分类的执行效率[4].针对这一问题,国内外研究学者通过构建各种特征降维的数学模型/算法,将多光谱/高光谱影像高维的光谱特征降为低维特征.在低维特征定义的空间中,属于同一地类的像元更凝聚,属于不同地类的像元更疏离,那么以此特征为依据,有助于提高影像分类的执行效率[5].
根据设计原理的不同,常用的特征降维算法可分为:线性降维型、非线性降维型等两大类.根据降维时是否有依据训练样本数据或先验知识,又可将线性降维算法分为监督型和非监督型[6].其中,线性判别分析 (Linear Discriminant Analysis, LDA)算法属于一种监督型线性降维算法,常用于多光谱/高光谱影像分类前的光谱特征数据降维.至今,国内外研究学者已从不同的角度对LDA算法加以应用或改进.如:谢欣芳等[7]结合线性判别分析 (LDA)算法和局部线性嵌入 (LLE)算法的思想,提出一种半监督局部判别分析算法;Liu Z等[8]结合稀疏图理论改进LDA算法,提出了一种正交稀疏线性判别分析算法;Ibrahim W等[9]将LDA与深度核化极限学习机相结合,用于蛋白质折叠子识别;M Mahdianpari等[10]基于LDA算法构建相干性矩阵,实现PolSAR图像的湿地分类;黄妙芬等[11]将LDA算法用于水环境石油类污染遥感识别;侯榜焕等[12]利用分类的先验知识对LDA算法加以改进,并提出了面向高光谱图像分类的半监督空谱判别分析方法;H Yuan等[13]提出了一种光谱-空间LDA算法并用于高光谱影像分类;W Sheng等[14]利用有类标像元数据和无类标像元数据训练LDA数学模型,使其能实现半监督的数据降维;A Phinyomark等[15]将LDA算法用于肌电特征投影;M Zhao等[16]通过马尔可夫随机场模型引入模糊隶属度,以此减少异常值对LDA算法的影响;Y Chao等[17]采用图切割法将数据集分成若干子集,基于成本最小化原则,采用LDA算法为每个子集找到最佳子空间,以实现特征降维;LuGF等[18]在假设所有训练数据均线性无关的前提下,提出了一种新的快速NLDA算法.
综上,虽然关于LDA算法的应用和改进已取得了较多的研究成果,但是大部分成果是通过结合其它技术理论对该算法加以改进,或者仅是拓宽了该算法的应用领域,属于松耦合改进的偏多,而关于算法本身原理方面的改进比较少.针对这一现状,本文从LDA算法原理入手,对其关键参数进行了重新定义,并提出了一种基于局部离散度的监督型线性判别分析 (Supervised Linear Discriminant Analysis based on Local Dispersion, SLDALD)算法,以下简称SLDALD算法.最后,联合World-View2影像数据,通过对比实验,对新算法的可行性和优越性加以验证.
1 原理和方法
1.1 线性判别分析(Linear Discriminant Analysis,LDA)算法[5]
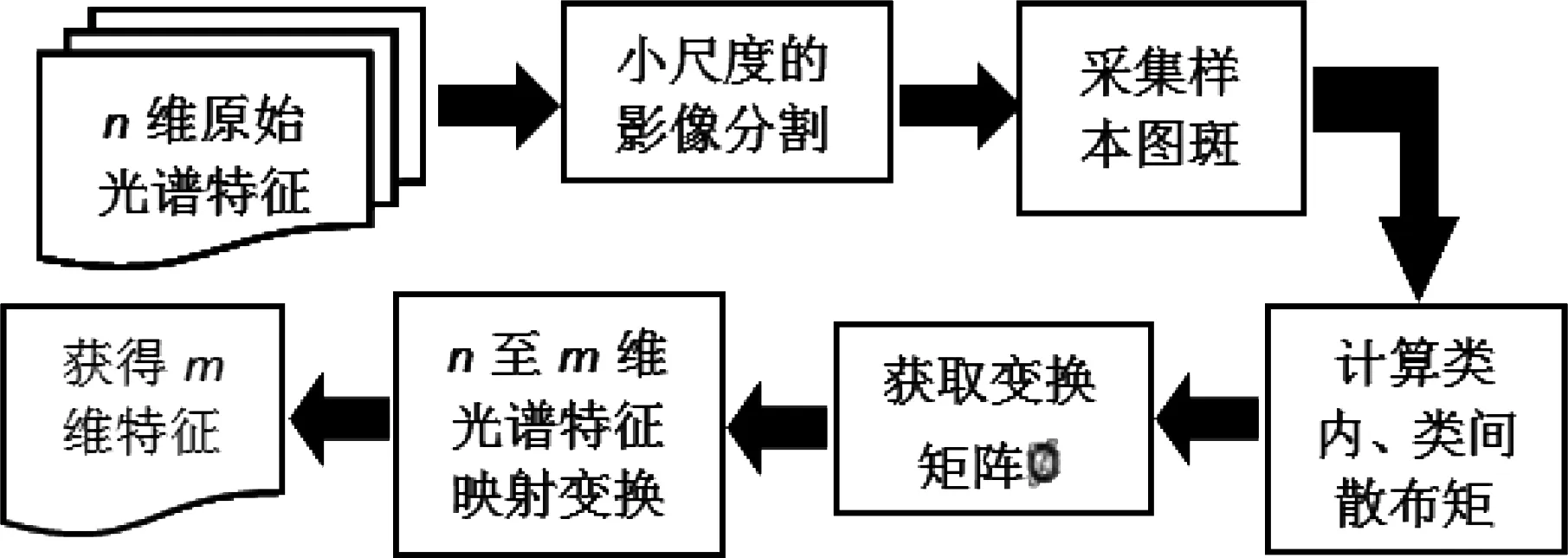
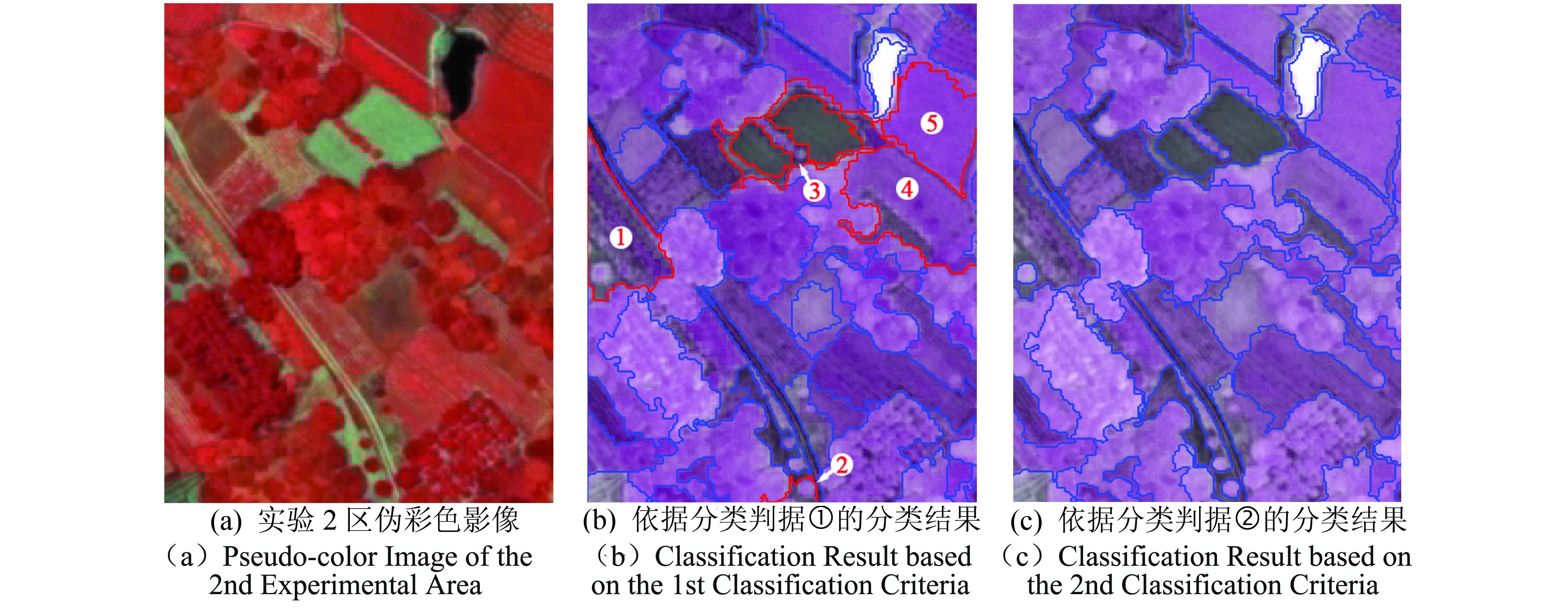
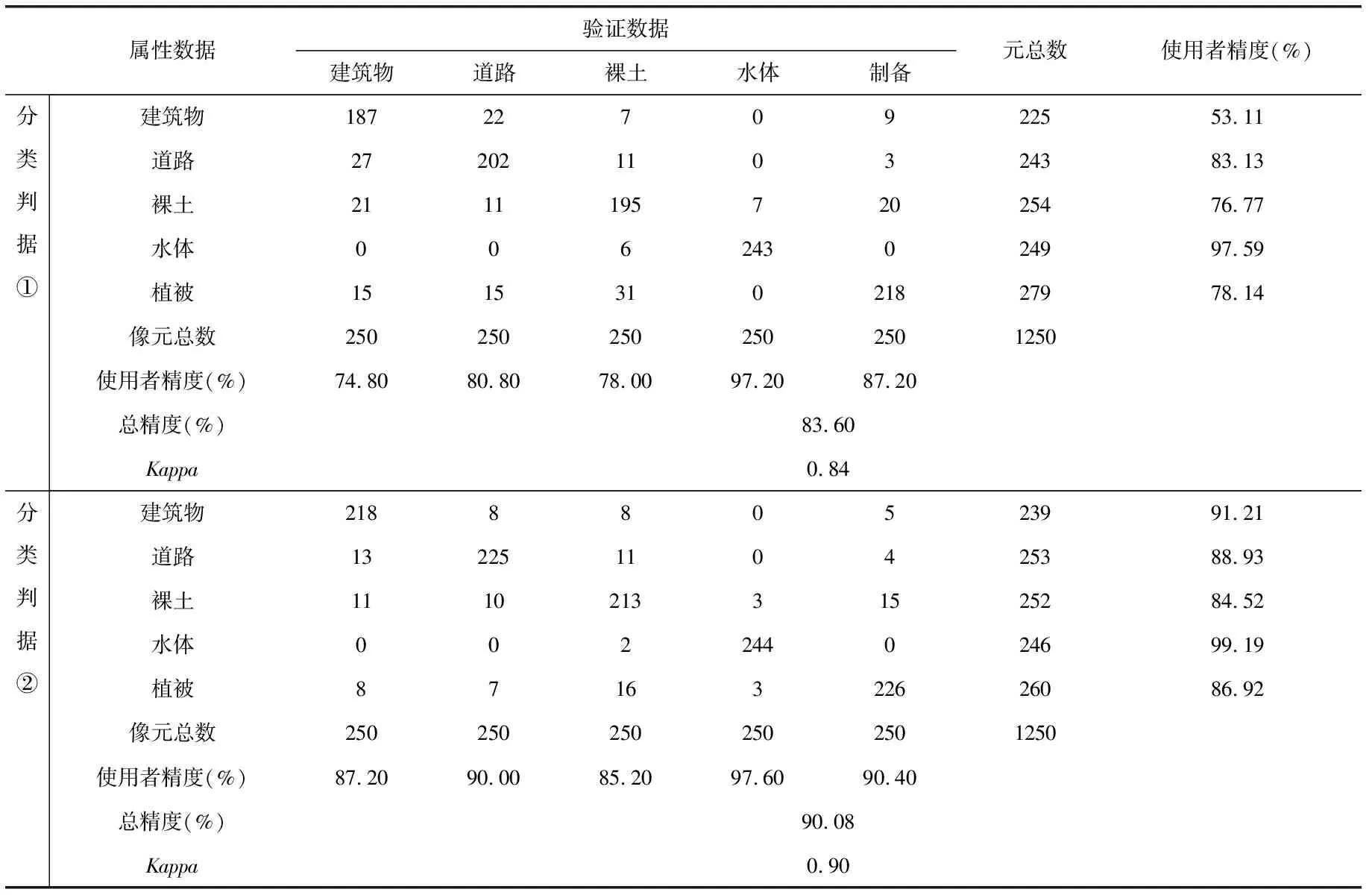
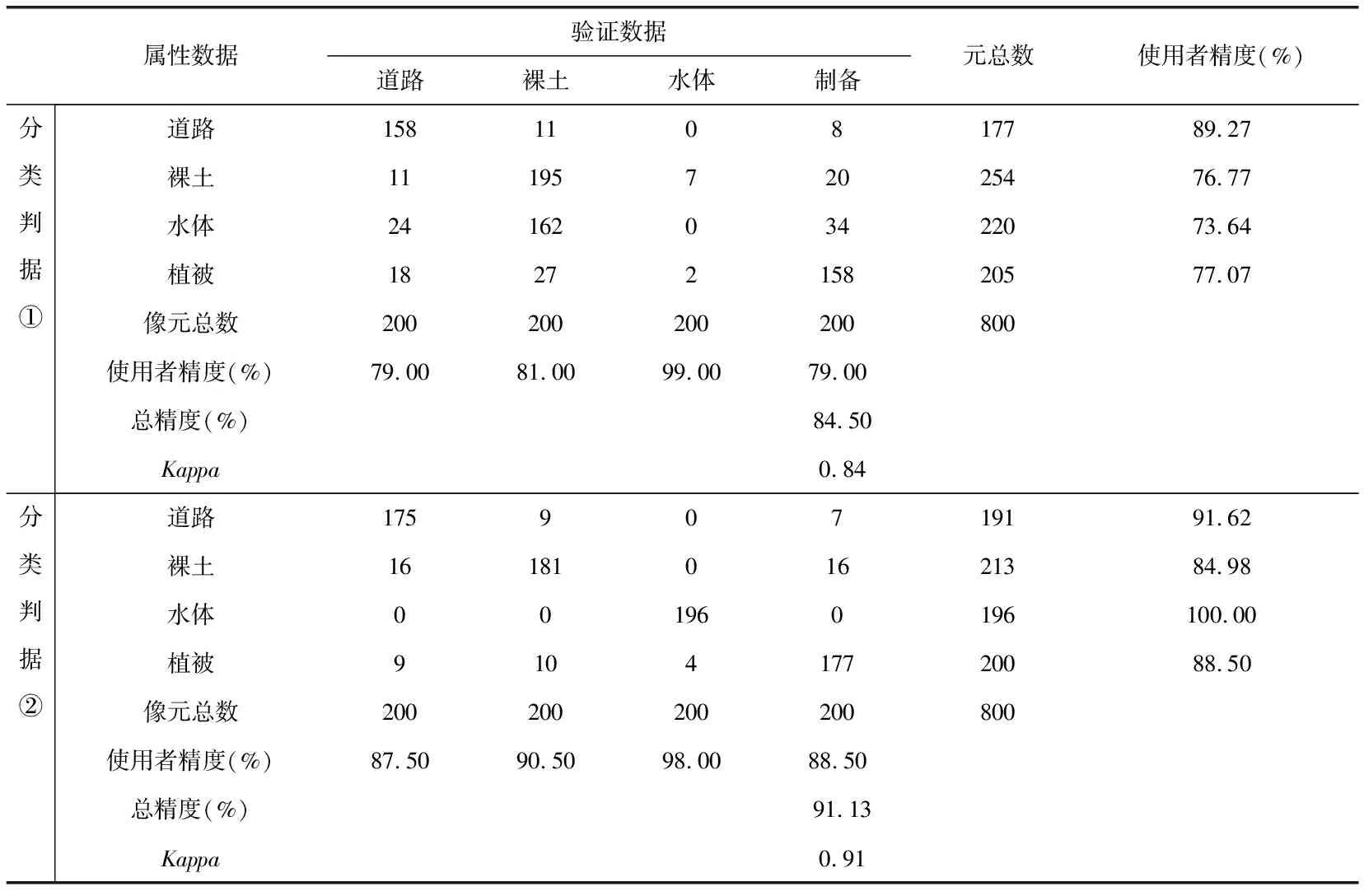
LDA算法的思想是:在影像包含的n维原始光谱特征数据中,采用正交变换方式,在保证信息损失最小的情况下,获得有利于分类的互不相关m维新特征数据,其中m 然而,在执行LDA算法时,从类的整体角度来定义像元光谱特征在类内、类间分布的离散程度(即离散度),而影像中不同区域内像元光谱特征离散度的差异并没有得到充分的体现,且降维过程易受噪声点的干扰.同时,在影像分类时,类边界处像元极易被误分,而用LDA算法进行特征降维后,此类像元光谱特征的类间离散度并没有得到显著提升.存在的这些弊端导致了依据LDA算法获得的低维特征,执行影像分类,分类效果不理想.本文以此为研究的出发点,提出了SLDALD算法,具体如下所述. 图1 SLDALD算法的执行过程Fig.1 Schematic Diagram of SLDALD Algorithm 本文所提SLDALD算法的具体执行过程为:首先,根据影像中包含的n维原始光谱数据,进行小尺度的影像分割.分割后,各图斑中所包含地物信息的类别尽可能单一.接着,根据影像中所包含的地类,采集代表C个不同地类的样本图斑,并利用C个样本图斑的n维光谱特征数据,计算类内散布矩阵、类间散布矩阵.然后,依据迹准则,利用类内散布矩阵、类间散布矩阵的前m个最大特征向量,获得变换矩阵Ø.最后,通过变换矩阵Ø,执行从n维光谱特征到m(m 图2 关于ω1类中像元iω1的类间邻域离散度图示Fig.2 Schematic Diagram of the about Pixel iω1 which belong to Class ω1 为了提取出有利于影像分类的特征,类内散布矩阵、类间散布矩阵的定义是解决问题的关键参数H根据LDA算法存在的弊端,本文从三个方面入手,改进两个散布矩阵的定义:1) 考虑到不同区域内像元光谱特征离散度的差异性,本文从像元邻域的角度出发,重新定义类内散布矩阵和类间散布矩阵;2) 鉴于在影像分类时,处于类边界处的像元极易被误分.为了让该类像元在降维后的特征空间中与同类像元更加凝聚,而与它类像元更加疏离,在计算类内、类间散布矩阵时,赋予类边界像元较大的权重,让后续的特征降维更针对此类像元;3) 考虑到特征降维易受噪声点的干扰,在计算类内散布矩阵时,赋予噪声点较小的权重,以抑制噪声点对降维过程的干扰. (1) ωk≠ωl ωk∈[ω1……ωC ] (2) ωk∈[ω1……ωC ] (3) (4) (5) 总的类间邻域散布矩阵SNB计算方式为 (6) (7) 图3 关于ω1类中像元iω1的类内邻域离散度图示Fig.3 Schematic Diagram of the about pixel iω1 which belong to Class ω1 (8) j≠i (9) (10) (11) (12) (13) (14) 1.2.3 特征降维 首先,分别计算出SNB、SNW的特征向量,并选出关于SNB、SNW前m个最大特征向量,组成若干个变换矩阵Ø.接着,根据不同的变换矩阵Ø,求出变换后的散布矩阵SWM、SBM (15) 最后,利用迹准则 (式16),计算出几种不同变换方案的J值.将最大J值对应的变换矩阵Ø做为映射变换矩阵,并执行n维光谱特征向量到m(m (16) 为了验证SLDALD算法的可行性和优越性,本文联合了寨场2012年World-View2影像,影像中包含了蓝色波段、绿色波段、红色波段、近红外波段1、海岸波段、黄色波段、红边波段、近红外波段2等8个波段光谱特征数据.为了避免实验中存在的偶然性,在影像中选取了两个实验区,两个实验区中均包含了:水体、植被、人工建筑、裸土等丰富的地物信息.实验1区大小459×493像素;实验2区大小381×488像素,两个实验区的伪彩色影像分别如图4a、图5a所示. 实验过程为:首先,分别采用LDA算法和SLDALD算法,将两个实验区影像原始的8维光谱特征数据降成2维,获得两组2维特征.在执行SLDALD算法时,通过对比实验,确定实验1区的最近邻像元个数取16;实验2区的最近邻像元个数取12.接着,分别依据两组2维特征,对两个实验区执行影像分类.其中,将LDA算法获得的2维特征称为分类判据①;将SLDALD算法获得的2维特征称为分类判据②.最后,将分类结果用蓝色的线条勾勒出来,线条以内的像元属于同一地类.为了更加客观全面地对两种分类结果的质量进行评析,本文采用了目视对比和影像分类评价指标 (即总精度和Kappa系数)等两种方式. 根据两个实验区的伪彩色影像 (图4a、图5a),采用目视对比的方式,分析对比2个实验区的两种分类结果 (图4b-c、图5b-c).对于实验1区来说,从依据分类判据①的分类结果 (图4b)可以看出:1) 4号地块内的耕地信息存在“分类过细”现象,且与相邻的植被信息存在“误分”现象;2) 2号地块内的植被信息与相邻裸土信息存在“误分”现象;3) 1号、3号、6号和7号地块的人工地物信息(包括:建筑物、道路)和相邻的裸土、植被信息之间存在“误分”现象;4) 5号地块的建筑物信息被误分,导致建筑物轮廓严重失真.因此,依据分类判据①,影像分类效果不佳.而在依据分类判据②的分类结果 (图4c)中,上述现象得到改善,各类地物的图斑边缘与其实际的边缘基本吻合,分类质量得到明显提高.对于实验2区来说,在依据分类判据①的分类结果中 (图5b): 1号~5号地块的植被与裸土信息之间存在较严重的“误分”现象,因此分类精度不高.而在依据分类判据②的分类结果 (图5c)中,上述的“误分”现象大大减少,分类质量得到明显改善. 图4 实验1区的伪彩色影像和分类结果对比Fig.4 Pseudo-color Image of the 1st Experimental Area and its Comparison of Classification Results 图5 实验2区的伪彩色影像和分类结果对比Fig.5 Pseudo-color Image of the 2nd Experimental Area and its Comparison of Classification Results 图6 植被、水体、建筑物、裸土等地物样本点的分布对比Fig.6 Comparison of the Distributions about Sample Points of Vegetation, Water, Buildings and Bare Soil 在两个实验区中,分别对被误分的植被、水体、建筑物、裸土等四类地物的像元进行随机采样,并用散点图的方式,显示这四类地物样本在分类判据①、分类判据②定义的特征空间中的分布状况 (图6). 从图6可以看出:在分类判据①定义的特征空间中 (图6a),建筑物样本点与水体样本点有部分重叠,水体与植被有也有部分重叠,而裸土样本点与植被样本点之间的可分性也不高.而在分类判据②定义的特征空间中 (图6b),植被、水体、建筑物、裸土等四类地物样本点分布得更加合理,属于不同地物的样本点更加疏离,而属于同一类地物的样本点更加聚集,各类地物的可分性得到了显著提高. 采用影像分类评价指标总体精度和Kappa系数,对两种影像分类结果做精度验证.具体为:分别在实验1、2区内,采用分区随机采样的方式,在植被、水体、建筑物、道路、裸土等各类地物信息中选取250、200个验证像元,并结合地面精度验证数据,对分类结果进行人机交互式的精度验证,精度验证数据如表1、表2所示.从精度验证数据可以看出:相比依据分类判据①的分类结果,依据分类判据②执行影像分类,实验1区、2区的分类总精度分别提高到90.08%、91.13%,Kappa系数均能达到0.9以上.因此,依据SLDALD算法获得的低维特征执行影像分类,能有效地提高分类精度. 表1 关于实验1区的精度验证数据Tab.1 Quantitatively Evaluating Data of the 1st Experimental Area 表2 关于实验2区的精度验证数据Tab.2 Quantitatively Evaluating Data of the 2nd Experimental Area 本文以影像分类为目的,对LDA算法进行了改进,并提出一种SLDALD算法.新算法从像元邻域的角度对类内、类间离散度进行重新定义,充分体现了不同区域内像元光谱特征离散度的差异性;同时,还突出了边缘点对特征降维的影响,并抑制了噪声点的干扰.最后,结合World-View2影像,通过分类对比实验证明:相比采用LDA算法所获得的低维特征,通过SLDALD算法所获得的低维特征空间中,不同地类像元的类间离散度得到了提高,相同地类的像元更加凝聚.以新算法所获得的低维特征为依据,执行影像分类,能有效提高分类质量.1.2 SLDALD算法

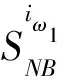




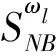
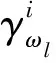
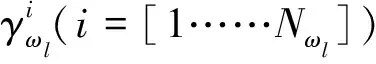



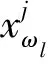
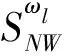
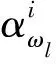


2 对比实验及分析
2.1 实验数据及结果
2.2 目视对比


3.3 分类结果的精度验证
3 结语
