存储系统中两级纠错编码方案设计与验证
2019-12-27罗金飞赵帅兵覃落雨王刚刘晓光
罗金飞,赵帅兵,覃落雨,王刚,*,刘晓光
1. 南开大学 计算机学院 天津市网络与数据安全技术重点实验室,天津 300350 2. 中国空间技术研究院,北京 100086
在恶劣的空间环境(如地球辐射带,相应的宇宙线)中,存在着大量的高能粒子[1]。这些带电粒子在穿过航天系统中的微电子器件时,在器件内部敏感区可能会产生电子-空穴对,这些电荷被灵敏器件电极收集后,造成器件逻辑状态的非正常改变或器件损坏。由于这种效应是单个粒子作用的结果,因此称为单粒子效应或单粒子事件[2]。
单粒子效应分为单粒子翻转、单粒子闭锁、单粒子烧毁等,其中单粒子翻转最为普遍。所谓单粒子翻转,是指星上存储单元在恶劣的辐照环境下受到高能粒子攻击时,可能会出现存储信息发生错误的情况,即原始写入数据为“0”,而实际存储器件中的内容却翻转为“1”,或者从“1”翻转到“0”,从而导致存储系统功能紊乱。
为保证在轨航天系统正常运行,必须设计相应的冗余措施来最大幅度地预防和消除相关恶劣辐照环境的影响[3]。
航天系统现有的软件防护措施中,有很多产品使用海明码[4]来进行错误检测与纠正[5],海明码纠一检二的功能降低了航天存储系统中不可修复的概率。但随着空间环境越来越恶劣,灵敏器件特征尺寸越来越小,造成单粒子翻转现象所需要的临界电荷也越来越低,即字内发生多个粒子翻转错误的现象越来越频繁[6],这时使用纠正一位错误的海明码就很难保证在轨航天系统的正常运行。
针对上述编码方案的不足,本文提出了一种两级冗余编码方案,来提高存储系统中的可靠性。该方案主要从以下两个方面进行:在字内选用纠错能力更高的编码,如使用可以纠正两位错误的BCH编码[7];在字间布置另一级冗余编码,例如可使用奇偶校验码[8],配合字内编码实现更强的检错/纠错能力。
这样在解码时,即可分为两种情况进行:当字内出现的错误位数在字内编码方案的纠错能力之内时,直接利用字内编码进行纠错;而当字内出现的错误位数超出字内编码方案的纠错能力时,可以将错误抛给上层编码,利用字间编码进行纠错。其中由于利用字间进行解码的情况发生概率显著低于字内解码,在所有故障事件中占较小比例,因此其带来的开销对系统整体平均性能影响较小。
这种编码方案构造思路有着显著优点:
1) 考虑单粒子翻转可能引起一个字内多个位同时发生翻转的情况。即不管一种编码的纠错能力有多高,都有可能出现不可修复的情况,并且一味地去提高一种编码方案的纠错能力需要付出很大时间与空间上的代价。本文提出的两级编码机制,用简单编码组合即可达到与复杂单一编码相当的可靠性,而在方案实现方面简单得多。
2) 不同的存储系统对可靠性和性能的要求有所不同。两级冗余编码可以针对不同存储器件的特点,例如程序存储器PROM,NOR_FLASH[9]本身属于只读型的存储器,可靠性较高,故可以在字内仍然采用低纠错的EDAC(39,32)编码,字间采用奇偶校验编码。而对于数据存储器NAND_FLASH和运行内存SRAM[10],这种自身可靠性较低、有较多写操作的,可以在字内采用高纠错码如BCH编码,字间采用奇偶校验编码。这样,就可以针对不同的存储器件的自身特点,平衡可靠性和成本性能。
1 存储编码
本文主要使用高纠错编码BCH或者错误检测和纠正(EDAC)技术中的海明码(Hamming)作为字内编码,奇偶校验码作为字间编码。下面对上述编码进行简单的介绍。
1.1 奇偶校验码
奇偶校验码作为常用的检错码,常用来检验传送的信息是否出现了错误。在事先知道码字错误位置的前提下,奇偶校验码具有1位错误恢复的能力。本文主要利用这一性质来恢复超过字内纠错能力的码字单元。
1.2 海明码
海明码[11]是一种纠正1位错的编码,星上系统CPU(BM383MG)采用一种Hamming(39,32)编码方案(下文用EDAC(39,32)表示)。该编码方案将32位信息位,编码生成7位监督校验位,码长为39位。
1.3 BCH码
BCH码是一种基于有限域的、可以纠正指定错误位数的线性循环码[12]。
本文采用的是BCH(44,32)。即32位信息位,编码生成12位监督校验位,码长为44位,具有纠2位错的能力。
1.4 纠错码与CRC校验的区别
CRC[13]校验中如果得到的余数不为0,则证明信道传输过程中码字发生了错误,此时会要求发送方重发。本文使用的前向纠错码利用码字间的校验关系恢复出正确的数据,此时并不需要通知发送方,故也谈不上重发,这也是与CRC校验最大的不同。
即CRC校验不具备纠错能力,当发现了错误之后并不能纠正出错误,而本文所使用的纠错码可以检查出是否发生了错误并且在纠错范围内纠正出来。
2 两级纠错编码方案设计
2.1 编码方案设计思想
本文提出了一种两级冗余编码方案,具体实现为通过简单编码的组合如字内使用Hamming码或者BCH码,字间可使用简单的奇偶校验码来组合高容错的编码。
这样当存储系统中出现错误但错误个数不超过字内编码的纠错范围时,可以直接利用字内纠错来进行纠正错误,无需利用字间编码进行纠错,这种情况也是最为常见的[14],这样也使得纠错时运算、访存的次数接近于原始字内编码;如果超过了字内本身编码的纠错范围,通过读入同条纹中其他字,利用第二级字间解码,利用字间运算,从而修复该错误条纹。
2.2 两级冗余方案设计
下面详细描述编码解码具体的过程:
编码操作:每个字先做字内编码,即通过乘以相应的编码矩阵来生成校验位,随后进行字间校验,同条纹的字(包括字内检验)按照第二级编码的编码规则做相关运算产生结果,生成第二级编码,得出最后的数据字和各自算出的校验位。
解码操作:首先进行字内检错,具体方式为将收到的码字乘以根据编码规则得到的校验矩阵,得到相应的伴随式。如果伴随式为0,则说明码字没有错误;如果不为0,需要查预先生成的伴随式与错误图样映射表,如果表中含有得到的伴随式,即说明可以通过字内修复,通过异或错误图样来进行纠正错误;如果没有,说明错误位数超过字内纠错能力,则读取同组条纹内其他字,同样进行检错、纠错、字内恢复的过程,进行字间恢复该错误条纹。
下面简单描述用第二级奇偶校验码纠错的过程,如图1所示,一组校验包含5行数据,分别为d0,d1,d2,d3,d4,字间校验为P0。假设d1发生了字内编码无法纠正的错误,则根据式(1)用编码时生成的异或条纹来进行异或操作即可恢复错误条纹。
d1=d0⊕d2⊕d3⊕d4⊕P0
(1)
式中:⊕为异或操作。

图1 两级纠错方案
Fig.1 Two-level decoding scheme
2.3 系统读写算法设计
2.2节描述的是数据字和校验之间的计算关系,而将两级编码引入实际的存储系统势必会带来编码读写性能的下降。本节主要是在此问题上,基于上述编码/解码的思想,提出相应的解决方案,尽量减少由于两级编码带来的对存储系统性能的影响。
2.3.1 系统写算法
本节主要讨论单字写产生的校验开销问题(多字写处理方法类似,整条纹写无更新问题,简单采用2.2节描述的编码方法即可)。
当向系统写入一个数据字时,一方面需要更新对应的内存字及其校验;另一方面,由于两级编码的引入,还需更新第二级校验的校验字,显然,与只采用字内校验的传统系统相比,会显著增大写延迟。为此,提出一种字间校验延迟更新的策略来减少第二级编码对存储系统写操作造成的影响,具体过程如下:
1) 系统初始化时生成一个专门负责整个系统的字间校验更新的队列并启动一个子线程(硬件实现可以是一个硬件队列和处理电路)专门负责字间校验更新。
2) 当写一个字时,首先计算字内校验,得到新值新校验之后,读取该字的旧值和旧校验,字间更新队列存储更新请求Δ=(新值与新校验)⊕(旧值与旧校验),随后可用来更新字间校验,最后写入新值新校验,返回给用户,此时用户感知到的更新过程结束。
3) 后台校验更新线程继续更新字间的第二级编码(以奇偶校验码为例,其他编码处理流程一致,校验更新计算不同):线程从系统初始化得到的更新队列中不断地取出更新请求Δ,读取旧字间校验XORold,计算Δ⊕XORold得出第二级编码的更新结果并将其写入,完成更新操作,一个写操作完整过程结束。
2.3.2 延迟更新策略的优点
1) 由于一级编码更新完成到二级编码更新完成这个时间间隔相对于故障/单粒子翻转事件发生间隔是极小的,所以可以认为对系统可靠性没有影响。而用户感知到的只是单一字内编码的延迟加上读取旧值和计算更新请求的开销,能够尽量降低第二级编码对整个的存储系统所带来的影响。
2) 可以灵活地根据存储器的可靠性特点选取第二级的编码,不必担心第二级编码的复杂度对整个存储系统所造成的影响。
3) 同一组的数据,可以同时进行更新而不必进行复杂的一致性处理。由于第一步只需要将新值与旧值的异或结果产生的中间变量暂存在队列里面,避免了同时读第二级校验条纹,这样就解决了同时更新同时读字间校验的冲突问题。
4) 对校验更新队列中的请求可实现更优的调度,例如可将同组的更新请求一次性执行,只需一次访存和多次异或运算,大幅度减少了访存次数。
2.3.3 系统读算法
系统读主要基于2.2节描述的解码操作的思想进行,具体方案如下:
1) 用户读取某个地址上的数据字时,读取该地址中的数据字和对应校验。
2) 首先进行字内检错,如果检错后发现无错误,直接返回用户即可。
3) 如果发现了错误但是不超过其字内编码的纠错范围时,进行字内纠错,随后将纠错得到的数据字返回给用户即可。
4) 如果错误个数超过了字内编码的纠错范围则进入第二级编码进行纠错。
3 编码方案算法优化
实验证明编码速度与系统的性能息息相关。编码速度越快,越有利于提高系统的吞吐率,提高系统的性能。纠错速度主要与系统的可靠性相关,也就是说修复时间越短,系统的可靠性越高[15]。基于此,本文还针对两级冗余编码方案提出几方面的优化方法,来提高系统的编解码效率,从而保证系统的可靠性。
优化工作主要从减少存储访问和优化编解码计算两个角度进行,其中优化访存主要应用读修改写来减少存储器的访问次数来进行;优化计算方面主要采用调度顺序优化和单指令流多数据流并行(SIMD)[16]。下面将详细介绍几种优化方法。
3.1 读修改写更新优化
在本文所提出的两级编码中,字间编码主要采用奇偶校验编码,即校验字为数据字的异或运算结果(如图1所示),注意到组中任何数据字的更新都会影响生成的校验字。本文采用读修改写[15]的方式来进行更新相应的校验条纹。
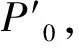
(2)
这样当需要更新一个字时,平凡方法(重构写)是将同组的其他字读出,然后进行计算,最后写入异或结果,需要访问6次访存才能完成该操作;而当运用了读修改写的方式,只需要读取该字和校验的旧值来计算新校验,然后写入新数据,新校验即可,只需要访问4次存储器即可,减少了大量的存储器访问次数。
这种方法的优化在实际硬件实现中,更能体现其优势,能够减少CPU访问内存的次数,大大降低CPU和内存之间速度的不匹配所带来的性能下降。4.3.1节描述的系统写方法即采用了这种策略。
3.2 调度顺序优化
编解码计算中存在一些重复运算,即,一些中间计算结果可用于其他计算,合理利用这种重复性可优化编解码计算。Plank等[17]基于此提出一种寻找较优计算顺序来减少重复运算的方法——调度顺序优化,从而降低总异或运算次数达到编码效率优化的目的。
本文借鉴此思想优化两级编码的计算。如图2所示,一个编码计算可表达为矩阵乘法运算B=AX,其中阴影部分表示元素1、空白表示元素0,A为校验向量,X为数据向量,B为结果向量。为了得到结果B,可直接逐个计算P0~P2,但这种方法并不高效。
可以看出,对于P0、P1两个元素的生成都包含中间异或结果x0+x3。若先计算出中间结果,再利用中间结果计算P0、P1,比直接计算可以节省1次异或运算。
图2的矩阵乘法,可利用图3所示的调度顺序进行优化,其中Si表示第i步运算。
传统寻找最优调度的算法是通过枚举所有调度次序来寻找最优次序,但对于本文EDAC(39,32)和BCH(44,32)这样的大规模编码并不可行,借鉴文献[17]中的Xsets启发式算法,设计了求解EDAC(39,32)和BCH(44,32)近似最优编解码计算调度次序的算法,算法说明如下:
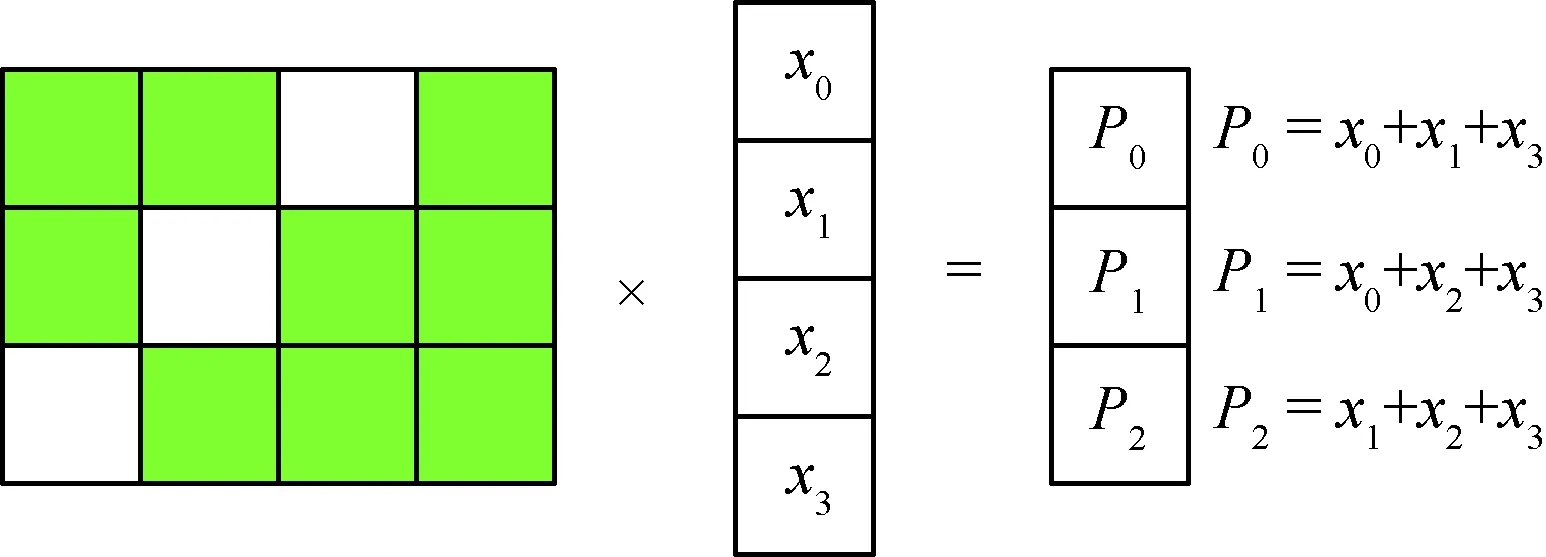
图2 编码操作的生成矩阵例子
Fig.2 An example that describing encoding operation
图3 一种优化调度方案
Fig.3 One optimization schedul
1) 数据位和中间计算结果作为集合里的元素。
2) 每个校验位用一个集合(称为Xset)表示。集合中元素异或得到这个校验位,初始时只由计算此校验位的数据位构成,在计算过程中,可能还包含中间结果。
3) 用图(称为Subex图)描述编码计算过程。顶点代表元素,边的权重代表两个元素共同出现在集合中的次数。
4) 启发式策略。权重最高的边的两个顶点生成新的元素,其异或结果作为新的元素插入到集合里。
算法流程图如图4所示。
通过使用Xsets算法寻找最优调度,平凡算法与优化后计算时异或次数相关对比如表1所示。由表1可见,通过使用相应的调度,优化后的异或操作可明显减少,其中BCH(44,32)编码异或次数减少了45.7%。
3.3 SIMD并行
当软件实现内存编码运算时,数据位提取和相应计算非常耗时,本项目针对此问题拟借助SIMD指令优化位运算[18]以提高数据并行性,来提高软件实现编解码的效率。
SIMD指令优化位运算具体过程为:
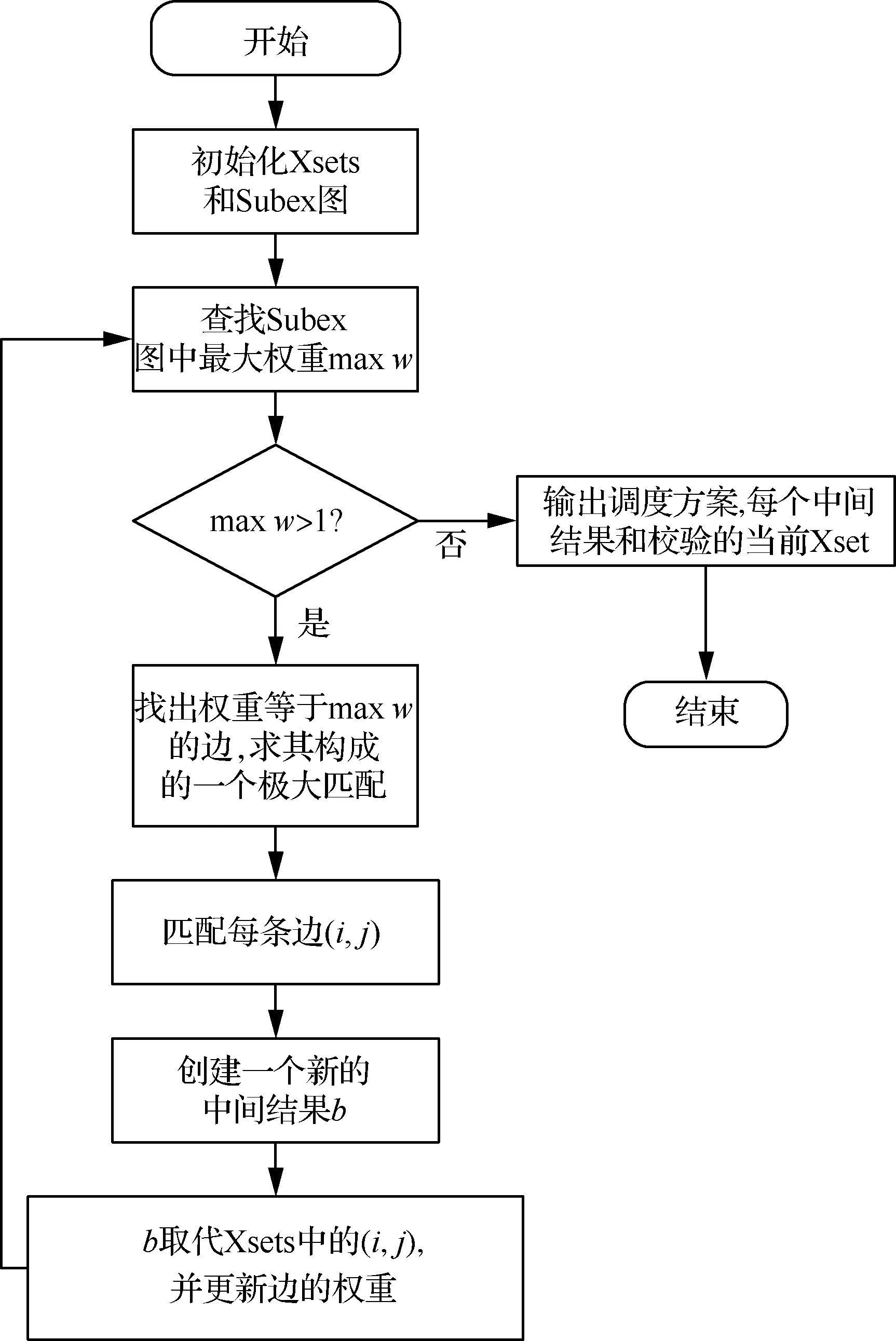
图4 Xsets算法流程图
Fig.4 Flowchart of Xsets algorithm

表1 异或运算次数对比Table 1 Comparison of XOR times
1) 基于编码的生成矩阵构造每个校验的掩码(校验位包含哪些数据位)。
2) 生成的掩码与需要编码的数据进行与(&)操作,得到校验包含的数据位的值。
3) 使用SIMD中popcnt指令[19]可一次得出数据位含有“1”的数目,数目的末位即生成的校验值。
4) 通过移位和或运算逐步生成所有校验码。
4 两级冗余编码方案分析
4.1 编码方案特点对比分析
表2主要列举了本文实现的编码相关特点。
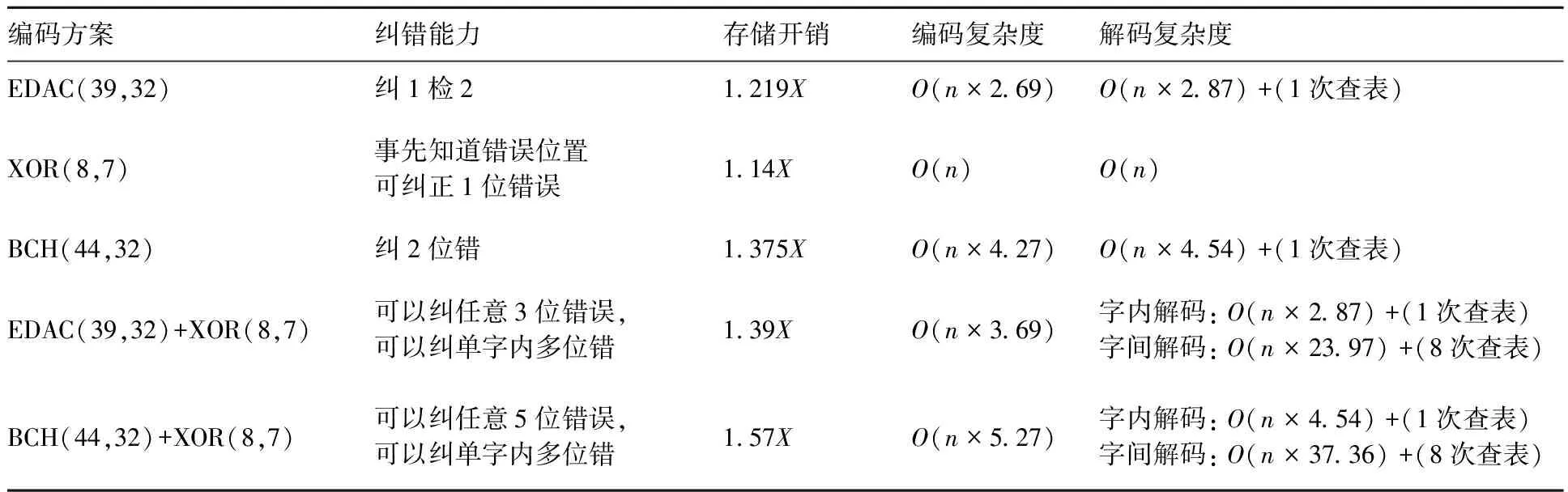
表2 编码特点分析Table 2 Analysis of coding characteristics
本文主要对比的是高纠错编码BCH(44,32)和两级编码EDAC(39,32)+XOR(8,7)的优劣。由表2可知,存储开销方面,两级编码EDAC(39,32)+XOR(8,7)的存储开销为(39×8)/(32×7)=1.39X(X为相应倍数,下同),与高纠错能力BCH(44,32)的存储开销(1.375X)相比几乎一致,但是在纠错能力上两级编码EDAC(39,32)+XOR(8,7)能够纠正同一编码条纹中的任意3位错,并且可以纠正单字内发生多个错误,而单一的BCH(44,32)只具备纠2位错的能力,即在存储开销相近的情况下实现了更高的纠错能力,并且编解码复杂度也比单一的BCH(44,32)低。
如果用两级冗余编码EDAC(39,32)+XOR(8,7)对比原始的EDAC(39,32),由于需要存储第二级的编码条纹,存储代价由原来的1.219X增加到了1.39X,这是两级编码的劣势,但对应的是纠错能力的大幅度提升,由原来的只能实现1位错到可以纠正同组的任意3位错误。
4.2 可靠性对比
本文采用二项分布计算不同编码方案下存储系统数据丢失的概率。假定空间单粒子翻转的概率ε=5.3×10-8upsets/(bit·day)[20](单位为每位每天翻转的概率),并且每个条纹里bit的翻转是独立分布的,利用二项分布式进行计算,得出航天存储系统采用单一的字内编码EDAC(39,32)方案,整个系统的不可修复概率为2.08×10-12;高纠错编码BCH(44,32)不可修复概率为2.43×10-15;当存储系统采用文章提出的两级冗余编码EDAC(39,32)+XOR(8,7)方案时,整个系统的不可修复性仅为1.21×10-22。
(3)
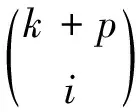
两级编码方案与原始的EDAC(39,32)编码、高纠错编码方案BCH(44,32)相比,两级冗余编码方案使条纹内出现不可修复的概率下降了十几个数量级,能够较好地保护星上存储系统的正常运行。
5 实验验证
本文为了仿真两级冗余编码方案在实际的星上系统中运行情况,通过软件模拟星上系统的方式来进行相关实验,基本运行环境如表3所示。

表3 实验环境Table 3 Environment experiment
5.1 内部存储器编解码计算效率
这部分实验主要针对两种字内编码方案EDAC(39,32)和BCH(44,32)及新提出的两级冗余方案,其中二级编码选用XOR(8,7)来进行内存系统中编码、检错、纠错测试分析。实验结果体现为相关计算性能,其输入分别为不同编码所需的生成矩阵、解码所需的校验矩阵和伴随式与错误图样映射表、随机生成的相应信息和每个条纹中随机生成的错误位置。
以编解码1 GB数据为例,测试结果如图5所示。由图中结果可得如下结论:
1) 字内编码方案与本文新提出的两级冗余方案相比,编码操作时间大致一样。
2) 检错方面,无故障读也大致相同;故障读时间,两级编码略高于简单一级编码,原因为当发生了字内编码不可修复的错误时,需要从内存中读同组的相关条纹,然后进行相关运算,其中读取内存和异或运算的过程消耗了一定的时间。
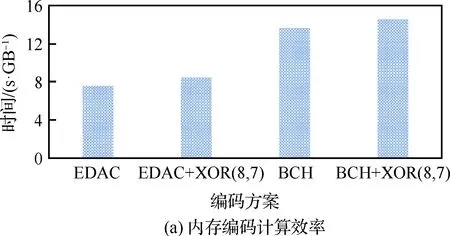
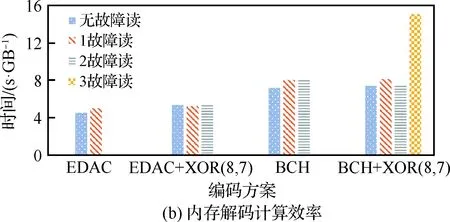
图5 内存编码和解码计算效率
Fig.5 Memory encoding and decoding calculation efficiency
5.2 内部存储器编码计算SIMD优化效果
测试了内存系统中SIMD对编码性能的优化效果,图6给出了对1 GB数据进行编码平凡算法(BIT_XOR)和SIMD算法所需时间。从图6可以看出,在内存系统中采用SIMD算法优化编码计算,较之平凡算法即按位异或算法显著提升了性能,最高达到了13倍加速比。
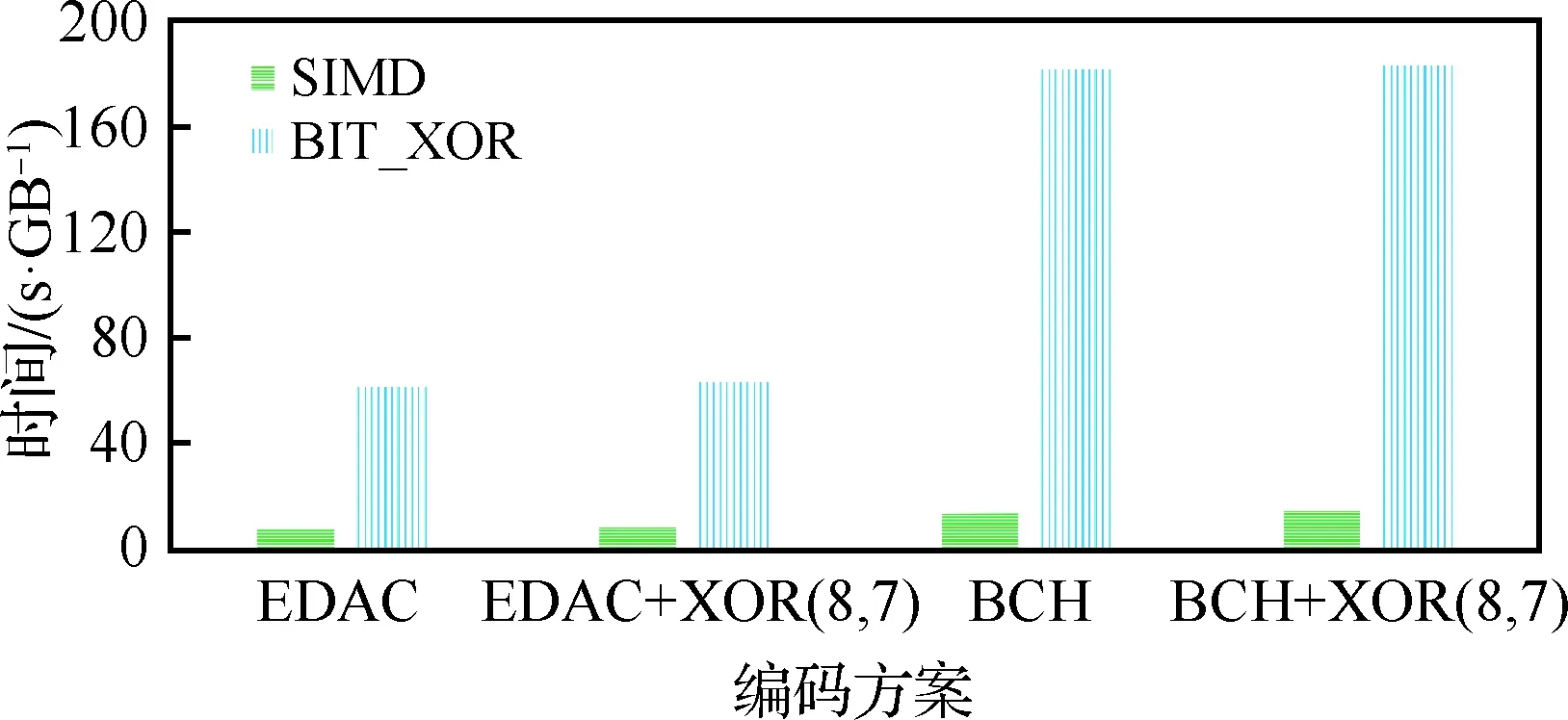
图6 SIMD和BIT_XOR优化算法对比
Fig.6 Comparison of SIMD and BIT_XOR optimization algorithms
5.3 外部存储器编解码计算效率
两级编码方案既可用于内存系统,也可用于外部存储器,此时编解码的基本单元由比特变为KB级的块。本节测试外部存储系统编码块大小为32 KB,二级编码仍采用XOR(8,7),编解码1 GB数据,其计算性能实验结果如图7所示。
从图7可以看出,类似于内存编解码计算性能,外部存储器两级编码计算耗时较一级来说有所增加;解码计算中多故障读时,由于要读同组的条纹进行检错、纠错,要比单一的字内纠错多耗费时间。
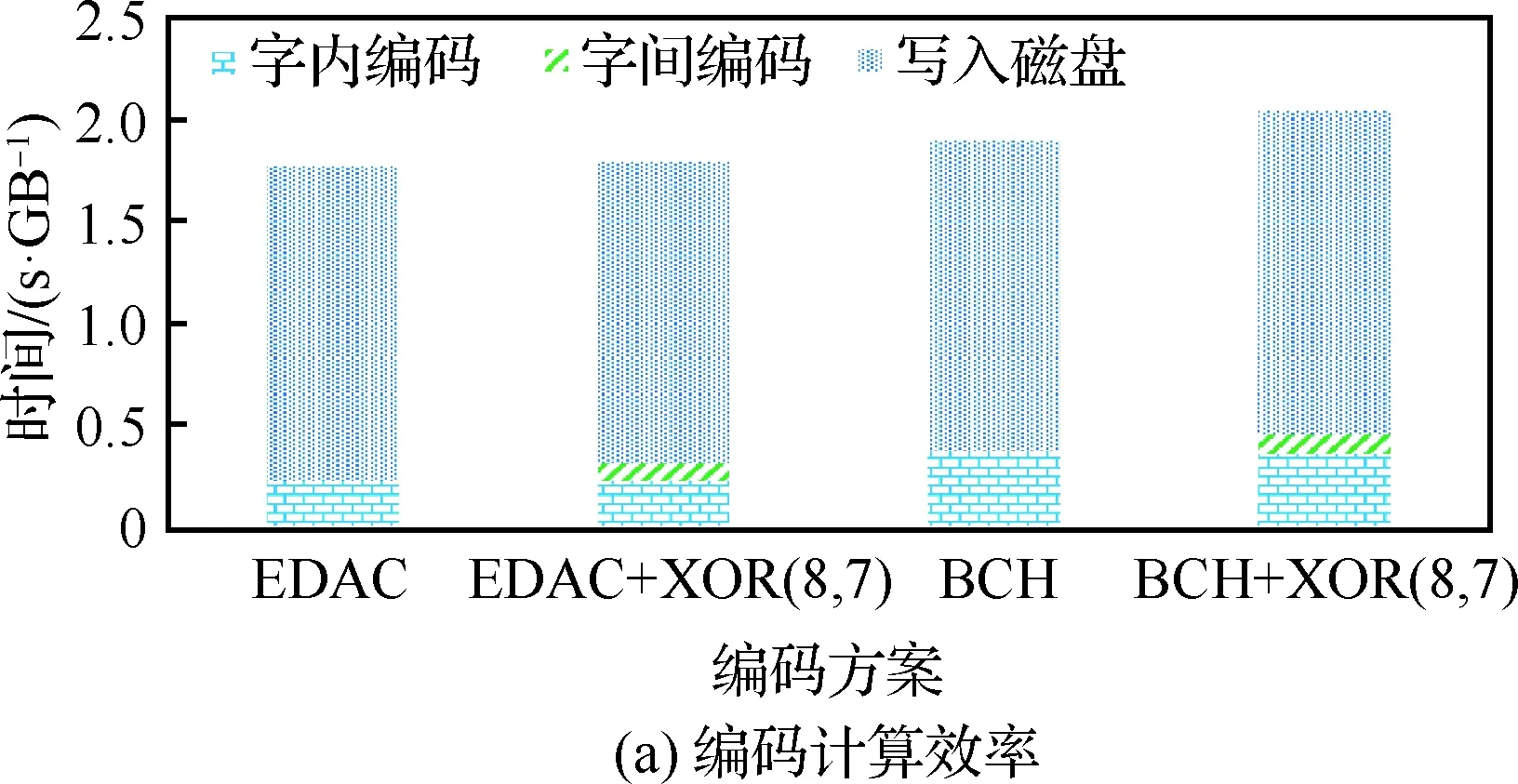
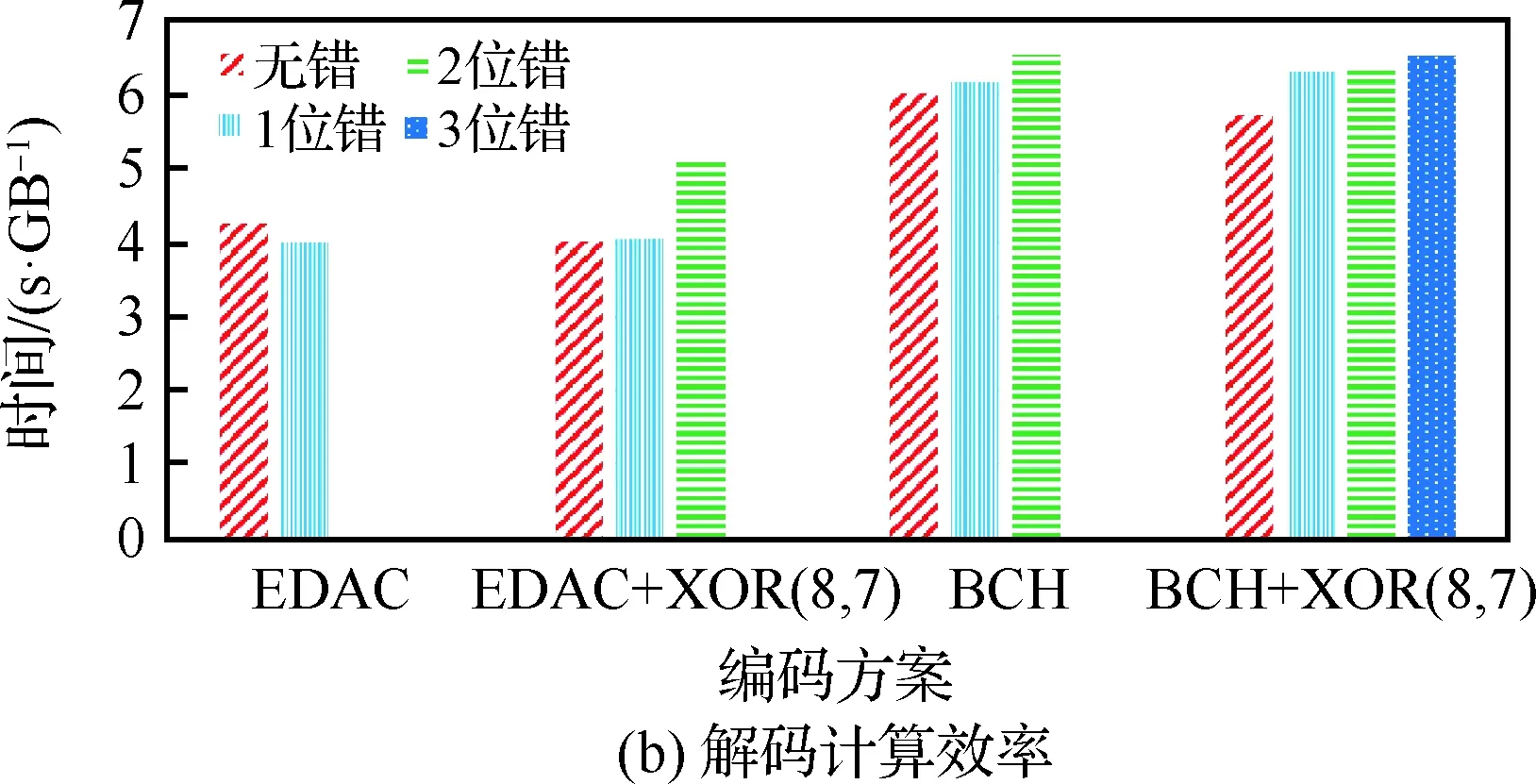
图7 外部存储器编码和解码计算效率
Fig.7 Disk encoding and decoding calculation efficiency
5.4 延迟更新优化效果
5.1节和5.3节的实验都是测试大量数据读写的吞吐率,花费的时间主要包括编解码计算时间和整条纹数据和校验的读写。在实际存储系统中,很多情况下是进行小数据量的读写,如内存系统中一个字的读写以及外存系统中一个块的读写,本节测试外存储系统中两级编码方案小数据写(更新)的性能,并测试延迟更新方法的优化效果。两级编码采用BCH(44,32)+XOR(8,7),对比一级编码采用BCH(44,32)。图8给出了实验结果,横坐标表示系统的编码块大小,纵坐标表示完成请求的响应时间。
通过图8可知延迟更新策略相比于同步更新策略对小写请求响应时间优化效果显著。BCH(44,32)+XOR(8,7)两级编码采用延迟更新策略后,即采取异步写模式后,较之同步写方式响应时间降低了30%~70%左右,即尽可能地降低了引入第二级编码条纹对存储系统的影响。
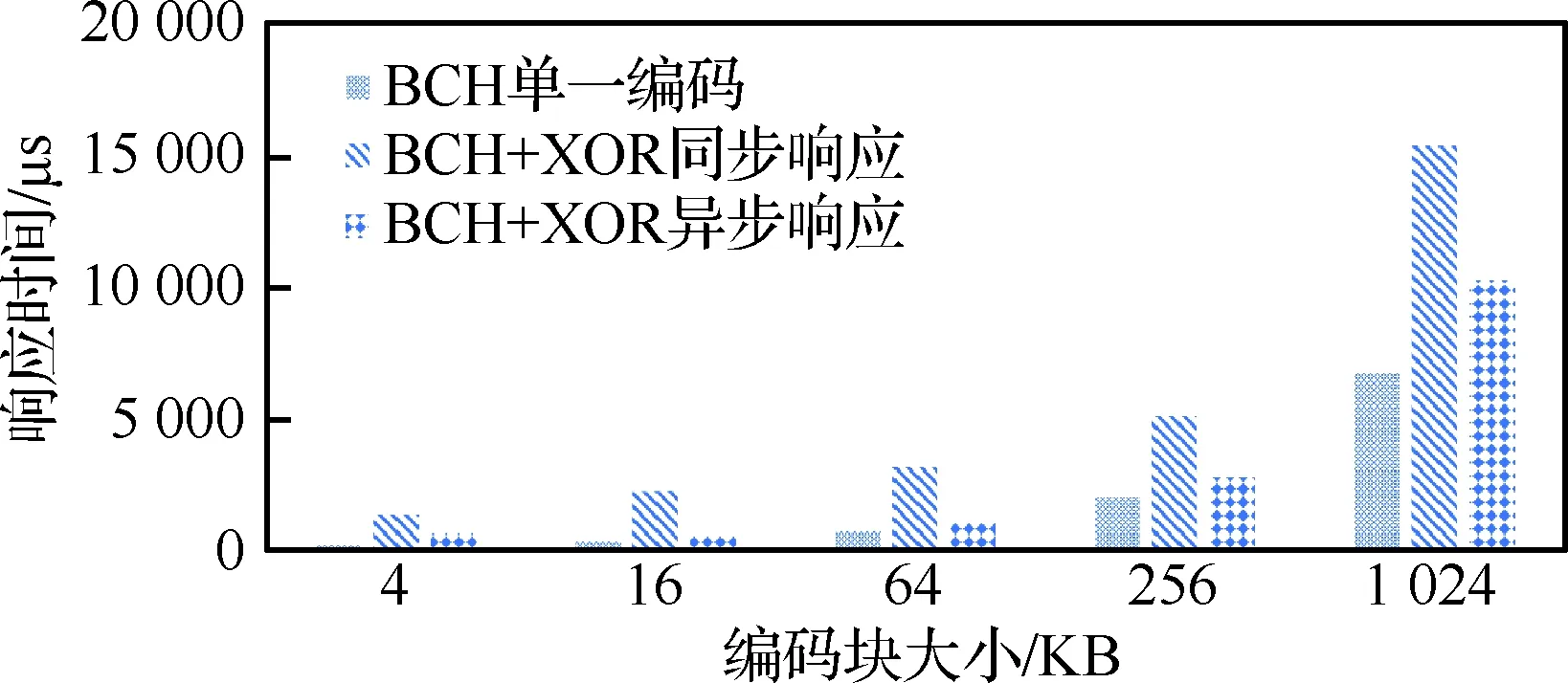
图8 延迟更新/正常更新机制性能对比
Fig.8 Comparison of delay update/normal update
5.5 调度次序优化效果
通过优化调度顺序,可以减少数据的运算量,从而提高处理器编解码的能力。图9给出了外存储系统中BCH(44,32)+XOR(8,7)两级编码方案编码1 GB数据平凡算法和调度优化的性能对比。横坐标为编码块大小,纵坐标为完成时间。
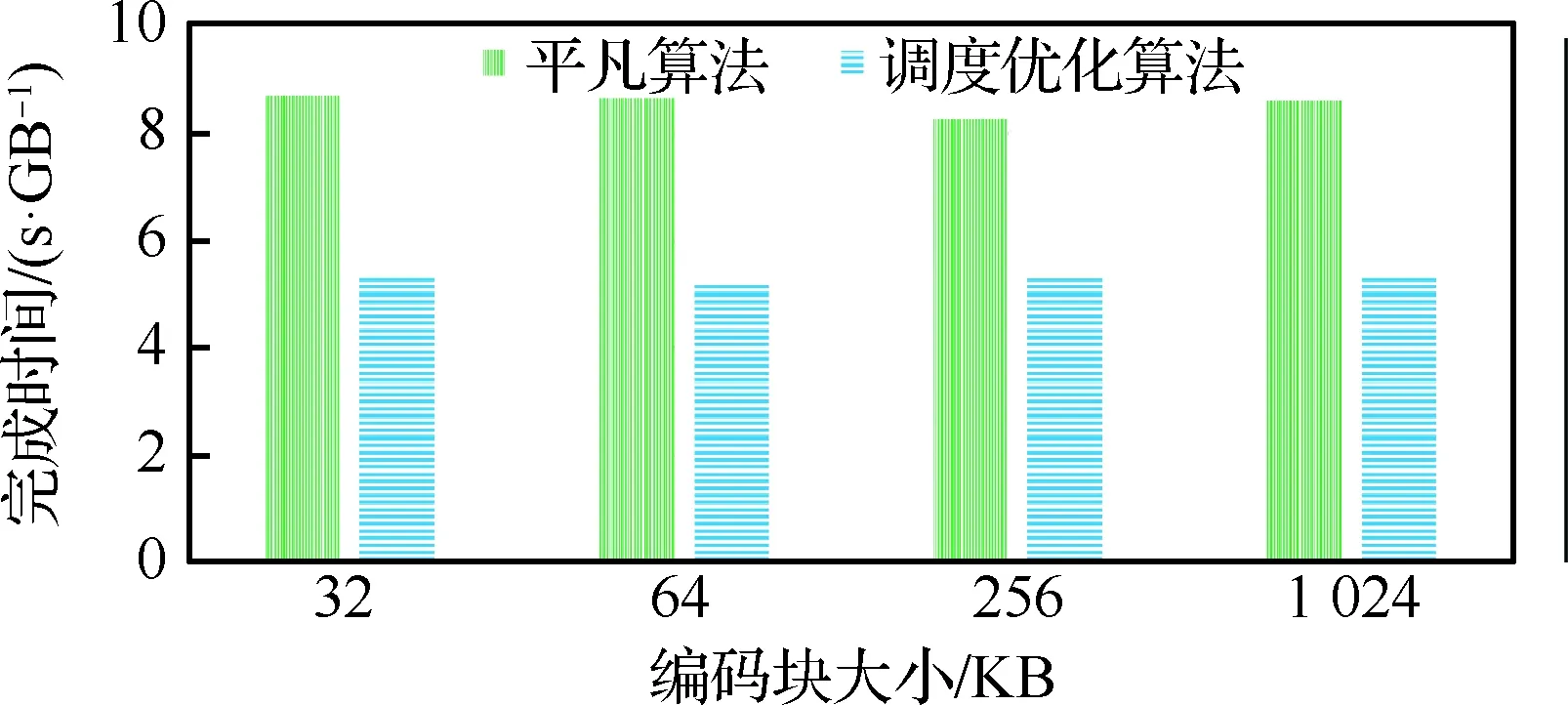
图9 平凡算法/调度优化性能对比
Fig.9 Comparison of original coding and scheduling order optimization
通过图9可知,在外部存储器中,与平凡算法相比,采用优化调度次序的效果明显,当编码的条纹单元大小为1 MB时,效率提升了39%。调度次序优化次序对解码性能的优化效果类似,限于篇幅未在本文中列出相应实验结果。
6 结 论
本文针对航天系统存储子系统提出了一种新的两级编码方案并提出了优化策略。
1) 通过简单编码的组合来提高编码纠错的能力,较之传统的以海明码为纠错码的系统,新设计的编码算法使存储系统中出现不可修复的概率大大降低,从而保障在轨卫星在恶劣辐照环境下的正常运行。
2) 采用延迟更新的方式,尽量减少由于两级编码带来的对存储系统性能的影响,即达到了在保证存储可靠性的同时尽量降低引入二级编码对系统更新性能造成影响的目的。
3) 针对提出的两级编码算法设计了一些优化算法,其中使用读修改写方法优化访存次数;采用Xsets启发式算法,利用图的相关性质寻找最优调度从而减少相关计算;使用SIMD并行优化位运算以提高编解码吞吐率等。
