斜激波极值规律的边界层影响

2019-12-27温浩史爱明鄢荣

航空学报 2019年12期

温浩，史爱明，鄢荣

西北工业大学航空学院 NPU-Duke空气动力与气动弹性联合实验室，西安 710072

超声速飞行器气动设计需要提高升阻比和降低音爆分贝值[1]。这两个问题的核心研究对象则是超声速飞行时必然会产生的激波。减弱甚至消除激波不仅可使超声速飞行的阻力减小[2]，还可通过降低激波强度(本文以激波后压强比激波前压强表征)直接减小近场音爆分贝值[3-4]。

激波强度存在随飞行马赫数变化的规律。正激波的强度由波前来流马赫数唯一确定[5]。对飞机设计来说，一维正激波强度规律是不够的。史爱明和Dowell[6]研究了二维斜激波中的斜激波极值规律，表明相同流动偏角下，必然存在流线穿过斜激波时激波强度最小的来流马赫数，且激波角与流动偏角在最优马赫数下呈现为线性关系。Emanuel[7]研究了斜激波后掠的情况，当气流偏角固定时，激波强度参数会随后掠角变化出现极值点，并得出极值点位置马赫数和后掠与否无关。Elaichi和Zebbiche[8]研究了总温对圆锥流动的影响，从其研究结果的分析中可以得出：当圆锥锥角固定时，激波强度参数随马赫数变化也存在极值现象。因研究对象的不同，Emanuel和Elaichi都未能指出斜激波极值规律的存在。

为对斜激波极值规律在黏性流动中的适用性进行研究，尝试将无黏流动中的斜激波规律拓展到黏性流动中。在黏性流动中，激波的最终状态不仅取决于几何外形，还会受到边界层的影响。对于可压缩流动中边界层流动参数，一般会结合Blasius不可压层流平板边界层解[9]进行理论计算。可压缩层流边界层的理论分析发展产生了变换方法[10-12]和参考温度法[13-15]，建立了可压缩边界层与不可压缩边界层参数间的关系。变换法对可压缩边界层方程进行简化，往往应用于边界层外流动参数与来流参数相差不大的情况[16]，对于复杂的工程应用来说精度较差。工程上则常用参考温度法进行计算，高超声速快速计算方法[17]、乘波体设计[18]均据此对边界层影响进行分析计算。湍流流动较为复杂，往往通过近似的边界层速度型分布得到边界层参数[19]；可压缩湍流边界层的理论计算主要是参考温度法[15]，变换方法则没有边界层厚度参数与Blasius解的关系研究。

本文建立了超声速流动中的黏性楔面激波模型，分别使用Eckert参考温度法[18](ERT)和Illingworth-Stewartson变换法[16](IST)进行了边界层影响的计算，并与计算流体力学(CFD)[20]方法得到的结果进行比较。结果表明，单一的ERT方法结果较CFD偏低，而IST方法则恰好较CFD偏高，且二者的这种表现规律在湍流情况下更加明显。因此建立基于ERT和IST的加权均值方法(WAM)。ERT的层流、湍流模型区别在于普朗特数导致的壁面温度恢复系数的差别；因湍流模型较为复杂，IST的湍流模型设置为与层流一致，忽略湍流项导致的差异。边界层理论模型的结果表明，黏性楔面激波同样存在着极值规律。

1 楔面激波理论模型

1.1 可压缩边界层及楔面激波

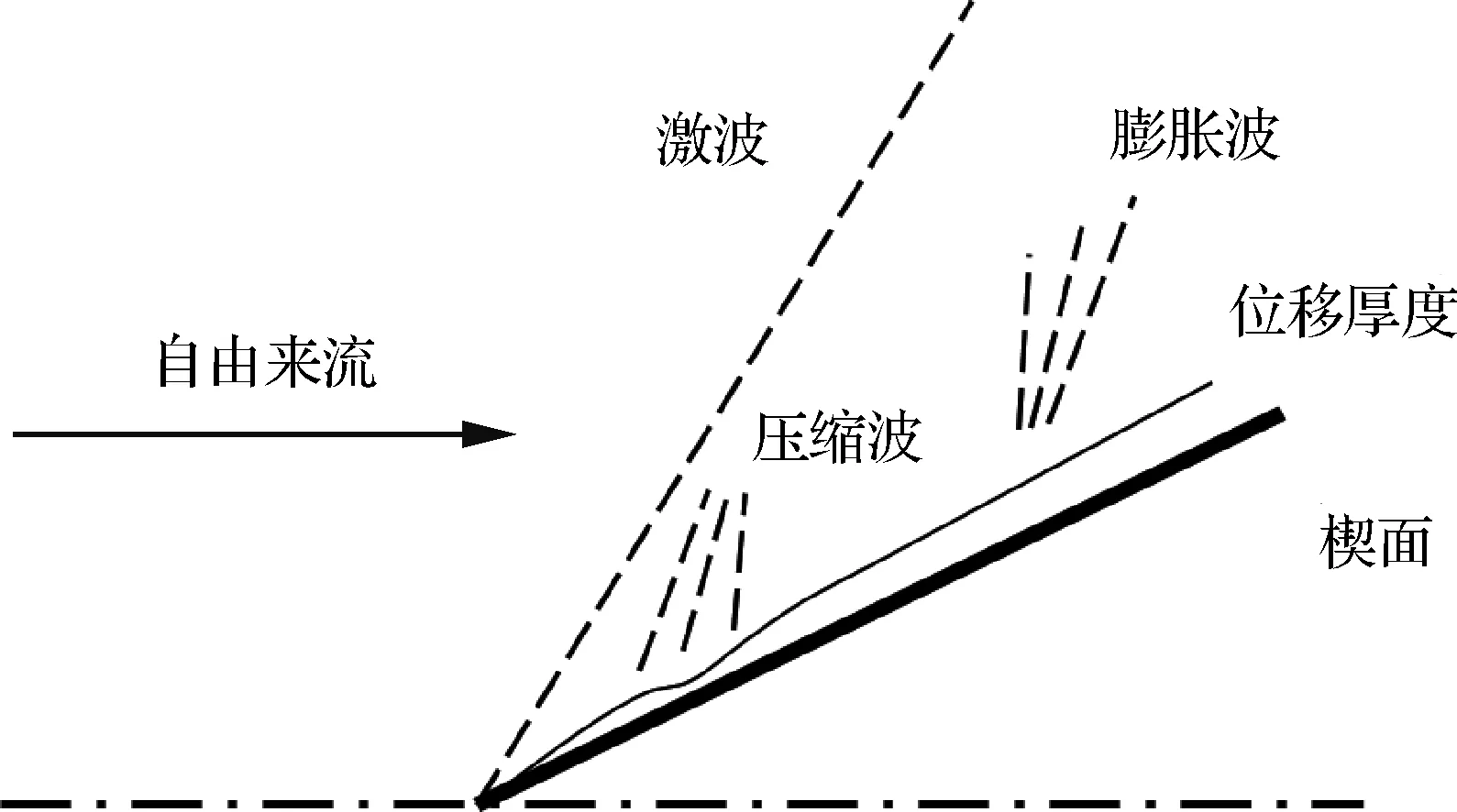
图1 超声速楔面黏性流动的激波结构Fig.1 Shock wave structure of supersonic wedge in viscous flow

楔面流动模型如图1所示，在超声速流动中存在一个二维楔面，楔面前不存在扰动。在特定的条件下，流体经过楔面会产生附体的斜激波；同时楔面附近因无滑移条件而产生边界层，使得边界层外的流线偏离楔面，偏离量可以用位移厚度表示。楔面模型边界层的发展与平板类似，在层流边界层和湍流边界层处，边界层位移厚度随楔面长度增加，其增长率降低，流线偏离自身，产生膨胀波；在边界层转捩处，位移厚度先减小后增加，根据位移厚度增长率的变化产生压缩波、膨胀波。因位移厚度变化率而产生的波与上游的激波相互作用，使激波略微弯曲：压缩波使得激波强度增加，激波角增大；膨胀波则反之。

斜激波理论中，气流方向的变化是激波产生的原因，经过激波的气流偏角θ是斜激波结构的一个重要参数。无黏楔面流动中，经过激波的气流偏角等于楔面与来流的夹角——楔面角θs，即无黏楔面激波结构具有θ=θs。黏性楔面流动中，边界层会导致气流偏角发生改变，全层流和全湍流时均具有θ>θs。1.2、1.3节将构建受边界层影响的气流偏角的计算方法，从而在1.4节中应用斜激波、膨胀波理论计算激波强度。

1.2 边界层外流动参数

平板流动中，使用边界层理论计算边界层位移厚度等参数时，主要基于自由来流参数。而在楔面激波模型中，为使得计算更加准确，考虑以无黏理论确定的斜激波后参数进行计算。主要计算激波下游的单位雷诺数Reds和激波下游温度T2。根据Sutherland公式计算黏性系数

(1)

式中:T为温度；参考温度Tv=273.2 K；常数c=110.4 K；黏性系数μ(Tv) = 1.72×10-5kg/(m·s)。

根据无黏理论，在已知来流马赫数Ma1和无黏气流偏角θs的条件下，可得激波后温度与激波前温度的比值T2/T1，从而得到激波后温度T2。

(2)

式中：T1=300 K为设置的激波上游温度；Man1为激波上游法向马赫数；γ=1.4为比热比；下标1表示激波前参数，下标2表示无黏理论确定的激波后参数，后文与此相同。根据式 (1)和式(2)，可以得到激波后黏性系数的比值μ2/μ1，进而由ρ1u1=ρ2u2(ρ、u为密度和速度)得到单位雷诺数之比及激波下游边界层外的单位雷诺数Reds，表达式为

(3)

其中:Reus为斜激波上游的单位雷诺数。

1.3 可压缩边界层计算方法

1.3.1 层流边界层计算方法

参考温度法模型以参考雷诺数来代替不可压缩Blasius解中的雷诺数，基于此进行边界层的计算，其模型的发展更多关注于参考温度的算法研究。ERT方法确定了参考温度T*，其表达式为

T*=0.5(Tw+T2)+0.22(Tr-T2)

(4)

根据参考温度法，得到参考雷诺数Re*=ρ*ued/μ*，其中：ρ*为参考密度；ue为边界层外速度；d=1 m为特征长度；μ*为参考黏性系数。根据理想气体状态方程ρ*=p*/RT*(p*=p2表示激波下游压强，R=287 J/(kg·K)表示气体常数)，可以得到

(5)

式中：μ*由T*确定。取距离楔面顶点水平距离x位置为层流边界层位移厚度的计算位置，则ERT方法确定的位移厚度为

(6)

求导可得x位置处流动方向相对楔面方向的偏转角θΔ，其表达为

(7)

那么最终x位置处流线方向相对来流方向的偏转角θef=θs+θΔ，如图2(a)所示。

变换法也可建立与不可压缩流动相似的可压缩层流边界层参数表示方法，该方法中Pr=1。对于ERT方法，Pr对最终理论模型结果的影响远小于模型与CFD结果间的差距，可以忽略不计；这表明ERT方法和IST方法间的差距不在于Pr的不同，而在于自身模型的构建过程。IST方法确定的位移厚度为

(8)

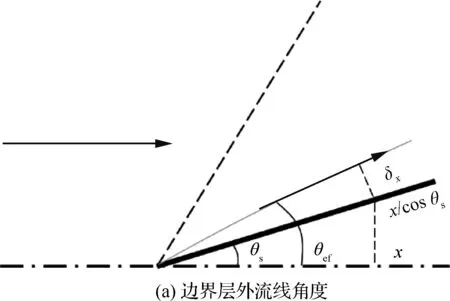
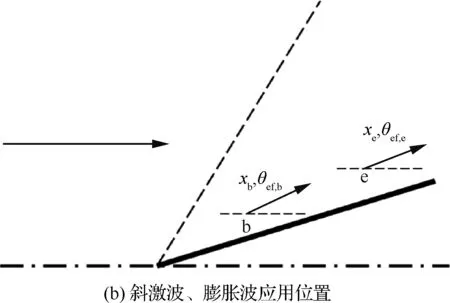
图2 考虑边界层影响的激波参数计算模型
Fig.2 Computation model of shock parameters with boundary layer effect considered

1.3.2 湍流边界层计算方法

IST法中，式(8)相关的不可压缩湍流边界层厚度为

其余参数不变。之后计算可压缩湍流边界层造成的流线方向改变量为

1.4 可压缩边界层流场影响

对于全层流或全湍流流动，在来流马赫数Ma1、楔面角θs、来流单位雷诺数Reus确定的情况下，随着距楔面顶点水平位置x增大，δx逐渐增大，但θΔ却逐渐减小。楔面流动中，楔面顶点附近壁面上会存在流动驻点，该位置处流动压强等于总压，之后随流动发展，压强会减小。在距离驻点足够远处，驻点总压的影响可以忽略不计。边界层理论可以确定不同x处的流线方向：x较小时，流动偏角增量较大；随x增大，流动偏角增量降低。

对于边界层影响量的计算，本文建立了斜激波和膨胀波的组合理论模型，用以计算x位置的无量纲压强px/p1，也称为激波强度。如图2(b)所示，在位置b处，使用斜激波理论确定位置b的流动参数，以之模拟流动驻点的影响。依据可压缩边界层理论计算初始位置的气流偏角θef,b；根据无黏斜激波理论，使用来流马赫数Ma1和气流偏角θef,b，确定初始斜激波强度px,b/p1等流场参数。假设b到e为等熵膨胀过程，根据b处流场信息，通过膨胀波理论和Prandtl-Meyer函数，计算e处对应的激波强度px,e/p1等参数。

膨胀波关系表示为

θef,b-θef,e=ν(Mae)-ν(Mab)

(9)

式中：Mab和Mae分别为b处和e处的马赫数；ν分Prandtl-Meyer函数，有

(10)

其中：α=Ma2-1。根据等熵过程总参数不变即可求得

(11)

进而得到e处的激波强度px,e/p1。

至此，在楔面激波模型中，将斜激波和边界层理论发展到了边界层外流场参数的计算中。边界层理论模型——ERT和IST方法会得出不同的激波强度计算结果。本节模型适用于边界层为全层流或全湍流的情况。对于流动转捩，需考虑转捩过程中边界层位移厚度的变化规律，同时在转捩前后分别应用层流和湍流理论模型。

2 理论模型预测精度分析

2.1 数值方法与网格

使用CFD的方法进行评估时，分别进行无黏Euler方程、层流Navier-Stokes方程、湍流基于雷诺平均Navier-Stokes(RANS)方程的计算。本文Euler方程空间离散为二阶守恒的单调迎风格式MUSCL[21]，与国内提出的无波动、无自由参数的耗散差分格式NND[22]相比，二者在数值计算的应用层面完全一致；限制器类型为Venkatakrishnan[23]，对流项处理的数值格式为Harten-Lax-van Leer-Contact (HLLC)[24]；时间离散为欧拉隐式(Euler-Implicit)；采用当地时间步、CFL数自适应、多重网格等方法加速收敛。层流Navier-Stokes方程无黏部分的离散格式与Euler方程一致，黏性项离散采用中心差分。湍流RANS方程湍流模型为Spalart-Allmaras(S-A)，湍流模型方程空间离散为一阶标量迎风(Scalar Upwind)格式，时间离散为欧拉隐式[20]。

二维超声速楔面黏性流动的计算网格如图3所示，采用非等距四边形网格。网格拓扑包括：与壁面平行的边界层网格，与激波平行的边界层外区域网格。沿壁面方向网格尺度最小为2×10-5m，线性增长，增长率为1.2，数据采集点处约为2×10-3m；垂直壁面方向网格尺度最小为4×10-7m，线性增长，增长率为1.2，数据采集点处约为7×10-4m。网格区域大小为0.4 m×1.2 m，总数为177×170；加密区域为激波和壁面附近，大小为0.03 m×0.02 m，数目为51×49。所有黏性CFD计算中，单位雷诺数Reus=3.5×107/m；所有CFD计算中，激波强度采集位置xe≈0.085 m。

图3 楔面激波数值模拟网格
Fig.3 Numerical mesh of wedge shock

2.2 理论模型中膨胀波部分的优化

本节及2.3节的CFD计算中，楔面角为3°，马赫数计算点取Ma1=1.195 7、1.234 9、1.319 0、1.368 6、1.469 1、1.600 0、1.700 0、2.000 0、2.300 0，其中Ma1=1.469 1产生的无黏激波强度最小。

理论模型中，对流动驻点影响的考虑在于xb处定义的激波强度计算，模型中膨胀波理论描述了边界层变化对激波强度的影响。模型中尚有xb未能确定，为分析其对xe处激波强度预测结果的影响，取Ma1=1.195 7、1.469 1、2.300 0结果进行研究。图4为层流ERT结果的理论模型计算值分布，可以看到在xb>0.01 m(约xe/8位置)后，预测结果随xb变化不大。在xb<0.01 m时，xb的影响较为明显。特别是当xb接近0时，与其他xb相比，理论模型预测结果会产生较大变化。这是因为边界层理论模型在xb为0时出现奇异值，使得预测的θΔ趋于90°。此时起始位置激波造成的压强增大，之后膨胀波造成的压强降低，二者在量值上都很大，造成最终计算精度的降低。xb>0.01 m后，xb影响的标准差为1.471 3×10-5，远小于理论模型与CFD结果间差值的标准差1.581 8×10-4；IST结果、湍流结果也是如此。这表明在处理简单的超声速楔面流动时，单一的斜激波理论可以达到较好的精度。因此，后续理论模型对于激波强度的预测，可以直接在xe处应用斜激波理论，采集点处压强写为px。

图4 初始激波位置xb对层流ERT预测结果的影响
Fig.4 Influence of initial shock locationxbon prediction results of laminar ERT model

2.3 单一ERT和IST理论方法结果分析

下面根据层流和湍流的数值结果对理论模型的预测结果进行分析。图5为理论模型预测结果与CFD间差距分析，图中CFD表示层流或湍流计算结果，WAM方法将在2.4节具体叙述。可以看到，无论是层流还是湍流，在激波强度的预测上，ERT、IST两种理论模型得到了随马赫数变化的极值现象，均与无黏理论表现一致。可以看到ERT的预测结果小于CFD结果，而IST的预测结果大于CFD结果，这在湍流结果中表现得更加明显。这说明两种边界层方法具有各自的内在特点，且分别表现了对结果的低估和高估。因此考虑两种模型的加权平均结果，以取得较好的黏性结果预测精度。

图5θs=3°理论模型和CFD计算结果的对比
Fig.5 Comparison between theoretical model and CFD results atθs=3°

2.4 WAM方法及其结果分析

WAM方法的表达式为

(12)

式中:λ为加权因子。ERT和IST方法均采用无黏激波后参数作为边界层参数来源。根据二者的理论方法构建过程，自变量参数可单一取为Ma2。

在λ的拟合上，考虑如表1所示的楔面角和来流马赫数范围来产生训练集和测试集。θs=3°、5°、10°在相应的马赫数范围内每组取9个马赫数点；而θs=20°、30°、35°时，每组取5个马赫数点。各楔面角下马赫数的设置基于激波强度极值规律，保证激波强度最小值点的存在。

Euler方程的计算结果表明，随楔面角的增大，数值结果与无黏理论值间的差距增大，即大楔面角下，CFD结果不够准确，如表2所示。层流和湍流的数值计算也是如此，故λ的拟合考虑角度θs=3°、5°、10°。因CFD结果与方程计算的精确值相比有一定的差距，但相较于理论与CFD间的误差，这一差距并不大。因此，采用层流结果难以训练出较为准确的λ值。而湍流结果中，这一误差相比之下却足够小，得到的拟合前的λ分布也较为稳定。且湍流与层流使用的是相同的可压缩处理方法，所以本文使用湍流计算结果来拟合λ，减少CFD本身误差的影响。

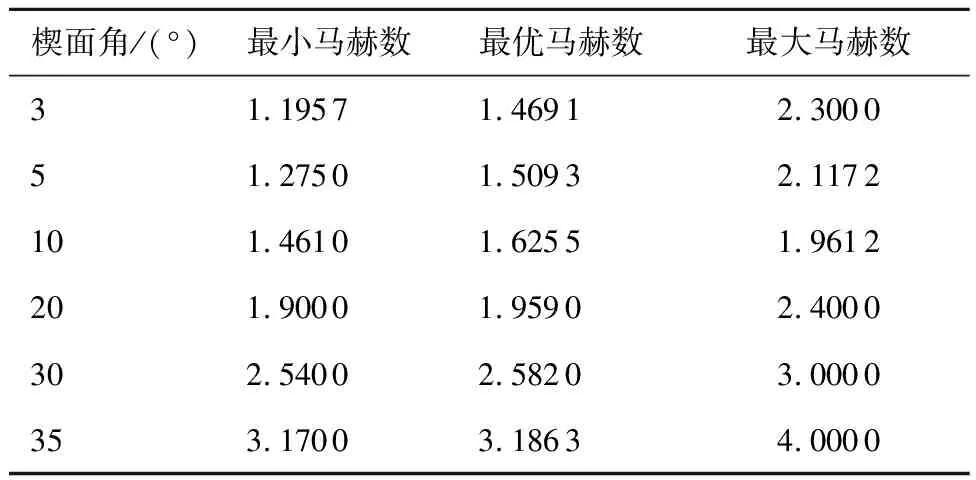
表1 CFD状态点范围Table 1 Condition range of CFD

λ经三次多项式拟合得到

(13)

下面对WAM模型的预测结果使用测试集进行分析，测试集选为全部计算黏性结果。WAM与CFD间的相对误差为

(14)

式中：i=无黏理论，层流WAM，湍流WAM；j=无黏CFD，层流CFD，湍流CFD。对同一楔面角下的所有马赫数结果相对误差求标准差，得到相对误差标准差分布如表2所示。随楔面角增大，WAM与CFD间的相对误差增大，在楔面角小于20°时，此时马赫数范围约为1.23.1，湍流WAM预测结果误差与其他楔面角和层流结果匹配较差，这表明WAM模型在楔面角约大于30°的湍流结果的可信度开始迅速下降，预测相对误差大于0.01；而层流结果则仍能保持一定精度。

表2 WAM与CFD间的相对误差标准差

在无黏斜激波规律中，随着流动偏角θ的增大，最优马赫数与激波恰好脱体时的马赫数间的差距逐渐减小，这意味着斜激波极值规律在大流动偏角，或者说高马赫数时，其适用性较差。因此对于所要研究的斜激波极值规律，WAM方法可以在合适的范围内取得较好的预测精度。

3 边界层对斜激波极值规律的影响

3.1 无黏斜激波极值规律讨论

无黏流动中的斜激波极值规律表明，在相同的气流偏转角θ下，具有最小激波强度的波前马赫数并不是激波恰好脱体的马赫数值，反而大于该值；称该最小激波强度下的来流马赫数为最优马赫数。该激波强度可以用压强比、总压损失率、温度比衡量，在激波强度于最优马赫数下取得极值时，压强比等参数均会取得极值。该规律基于斜激波理论得到的法向马赫数关系式为[10]

(15)

式中：θ为经过激波的气流偏角，在无黏的超声速楔面模型中，其等于楔面角θs；β为激波角，即激波面与来流方向的夹角。此关系式建立了斜激波空间结构参数θ、β与激波强度唯一变量Man1的关系。基于此，得到最优马赫数为

(16)

同样地，在确定马赫数作为飞机设计约束、要求更小的飞行能量损失的情况下，穿过激波的流动偏角会趋向于0。因此在没有其他约束作用的情形下，无法合理地设计出具有一定体积的超声速外形，亚声速飞行器设计也是如此，空气动力学特性决定了更小飞行能量损失的飞行器永远是厚度更小的类似设计。上述斜激波极值规律表明对于楔面激波，尽管在给定马赫数下不存在最优的飞行器设计，然而一旦根据其他约束条件确定飞行器外形，那么便可以使用极值规律衡量飞行器外形和马赫数需求的匹配度。

关于直接由飞行器外形变化产生的附体斜激波，主要有两种形式。其一是本文研究的楔面激波类型，特点是斜激波的上游不存在边界层[25]；其二为楔角流动类型，斜激波前存在边界层，因此产生的斜激波与边界层相互作用，使得激波振荡，流场与无黏理论解间差距较大[26-28]。这为斜激波极值规律的应用提供了新的思路，比如对于楔角流动所产生的斜激波，其最优马赫数如何变化、其振荡幅值和频率是否表现对称性，这都是可以深入研究的方向。此外，经典的入/反射激波与平板边界层相互作用，分离泡、流动转捩的相关特征会如何变化，这是斜激波极值规律应用的另一个探索[29-30]。

3.2 最优马赫数及激波强度变化

数值验证的结果表明，在最优马赫数附近，楔面角不大时，WAM方法取了得良好的精度。

首先考虑最优马赫数的变化。在加入了黏性边界层的影响后，楔面角θs≈3°～20°范围内，关于最优马赫数的变化，层流增量为0.001 5～0.003 3，湍流增量比层流稍大，为0.002 8～0.006 1，且二者均随楔面角增大而增大。图6为加入边界层影响后，最优马赫数Ma1随θs变化的情况。这表明边界层不会使得该Ma1产生较大变化；由局部放大图可知湍流Ma1增量约为层流2倍，20°时的增量约为3°时的2倍。

根据楔面边界层变化规律，在距楔面顶点水平位置大于参考位置0.085 m处，最优马赫数的增量会更小，反之则更大，这里取θs=10°进行讨论。在百倍于参考位置，即约10 m处，黏性最优马赫数的增量相比参考位置减小，层流不大于0.000 2，湍流不大于0.000 6。在距楔面顶点约0.01 m，接近理论模型奇异点处，最优马赫数增量比参考位置增加，层流和湍流均不大于0.000 6。这表明在约0.01～10 m的较大范围内，于参考位置0.085 m处得出的最优马赫数的变化规律可对整个区域的结果进行表征。所以之后的讨论仍是基于参考位置的数据。

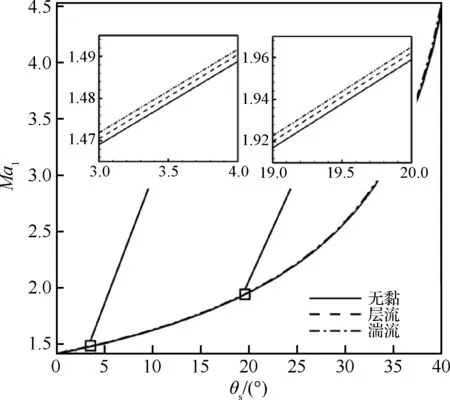
图6 边界层对最小激波强度马赫数的影响
Fig.6 Changes of Mach number of minimum shock strength influenced by boundary layer

其次考虑激波强度受到的影响。激波强度增量Δ(px/p1)与最优马赫数增量类似，其相比无黏激波强度值变化很小。图7为层流状态下，激波强度增量Δ(px/p1)的分布。图中：LMS表示无黏最小激波强度线，有黏下的最小激波强度线基本与无黏结果一致；βs指无黏超声速楔面模型中，由Ma1和θs经无黏斜激波理论确定的激波角。图中激波强度增量分布存在极小值点，极值点马赫数大于最优马赫数。

图7 激波强度增量分布
Fig.7 Distribution of increments of shock strength

3.3 激波强度变化的理论解释

为理解从无黏斜激波关系到加入边界层影响后的激波强度和最优马赫数的变化，将受边界影响的激波强度px/p1表示为无黏激波强度项与激波强度增量项之和：

(17)

式中：p2/p1为无黏激波强度。根据斜激波理论，激波强度自变量取为来流马赫数和楔面角，即p2/p1=f(Ma1,θs)。并且最终，边界层导致的流线偏角变化仍是代入无黏斜激波理论，从而计算激波强度变化。根据无黏斜激波理论，Δ(px/p1)的一阶展开为

(18)

其中：

(19)

图8为无黏激波强度梯度项∂(p2/p1)/∂θs和层流流动偏角增量θΔ的空间分布。无黏激波强度梯度项的极值点马赫数异于最优马赫数。层流流动偏角增量项不存在极值点，其随马赫数单调增加。

图8 激波强度增量项的分解结果
Fig.8 Terms decomposed from increments of shock strength

图9为LMS线上湍流和层流情况下的激波强度增量比值及流动偏角增量比值。LMS线上，湍流自约θs=37.9°开始激波全部脱体，而层流自约θs=40.4°开始脱体。图9中，在较大的楔面角范围内，激波强度增量比值和流动偏角增量比值保持了较好的一致性：楔面角小于20°时，二者相对差距不超过0.5%；在楔面角小于25°时，二者相对差距不超过1%，在楔面角小于30°时，二者相对差距不超过2.5%。因此，在WAM-CFD误差较小的楔面角范围内(3°～20°)，Δ(px/p1)使用式(18)预测，其误差相比精确的斜激波理论不大。在楔面角大于35°后，二者差距已超过7%，此时不宜使用式(18)进行Δ(px/p1)的预测。

图9 LMS线上湍流和层流偏角增量、激波强度增量比值
Fig.9 Ratio of increments at turbulent and laminar case for deflection angle and shock strength at line LMS

至此确定了在LMS线附近的区域内，边界层导致的激波强度增量和其导致的流动偏角增量呈较为准确的线性关系，系数为无黏激波强度梯度项。相对于激波强度的极值点马赫数，激波强度增量与激波强度梯度的极值点马赫数均较大，这一分布关系使得最优马赫数增大。

4 结论

1) 建立了黏性楔面激波强度计算的理论模型，初步定量地确定了边界层厚度对楔面激波强度影响规律，为超声速黏性楔面流动问题研究提供了精度尚可的斜激波参数理论计算方法。通过研究计入边界层等效厚度影响的斜激波强度极值规律随马赫数、楔面角的变参规律，将斜激波强度极值规律拓展到了黏性楔面流动范畴。

2) 理论模型显示：① 边界层位移厚度使斜激波极值规律最优马赫数略微增大，增加量在千分位；② 当楔面角小于20°、马赫数小于2.3时，理论模型结果与CFD结果的相对误差不大于0.1%；③ 层流与湍流边界层对斜激波极值规律的影响程度不同；湍流边界层导致的气流偏角增量约是层流边界层的2倍，最优马赫数增量也约是层流边界层的2倍。

3) ERT和IST的加权模型仅适用于全层流或全湍流流动，且对于高马赫数(Ma>2.5)和大楔面角(θ>30°)情况，预测结果开始变得不理想(相对误差大于0.2%)。计入转捩因素的楔面斜激波理论模型是进一步的研究方向。文章讨论了楔面上游为自由来流的楔面斜激波，楔面上游为壁面的楔面斜激波则是接下来的研究内容。这两种激波是超声速飞机内、外流问题生成斜激波的主要形式。