排气门升程对排气道流通能力的影响规律
2019-12-27芮静敏徐洋
芮静敏,徐洋
(1. 北京电子科技职业学院汽车工程学院,北京 100176;2.北京理工大学机械与车辆学院,北京 100081)
内燃机作为动力源,广泛应用于工业、农业、军事等领域。随着全球能源和环境的不断恶化,在对内燃机的研究中,保证其动力性的同时,人们更加注重其经济性和排放。进排气系统作为内燃机的重要组成部分,直接影响内燃机的性能指标,因此对进排气系统的优化设计显得尤为重要。而进排气系统与进排气道、进排气门大小以及升程有密切关系,国内外对此进行了大量研究。
B. Semlitsch等[1]采用大涡模拟(LES)方法,研究了气门和活塞运动对排气道能量损失和流量系数的影响。S. Babu等[2]对柴油机排气道模型采用大涡模拟和Reynold模拟方法,结果发现在气门附近流域动能损失严重。MackliniDalla Nora等[3]研究了排气门升程和排气背压对某二冲程GDI发动机性能的影响,结果显示,高转速时排气背压对充气效率影响较小,低转速时可以通过适当减小最大排气门升程来提高充气效率。
康彦红等[4]使用Fluent软件对不同气门升程的排气道流场进行CFD数值模拟,并将计算结果同试验数据进行对比,发现两种方法获得的流量数据吻合良好,指出了排气道改进的方向。崔洪江[5]通过稳流试验,得出进排气道在不同气门升程时的流量系数和进气道的涡流比,并运用CFD对进排气道在不同气门升程下进行计算,对比试验值和计算值,结果表明,采用分区域设定湍流模型的模拟计算结果精度高于仅采用一种湍流模型的流场计算结果,并根据计算结果对气道进行了多种优化。王建[6]对排气道进行了稳流气道试验,并使用Fire软件计算了排气道三维流场,研究了气门升程、气道截面形状等不同结构参数下的气道流场及规律。对气道的截面形状等进行了优化,给出了通用小型汽油机气道的评价量值。
以上研究主要是针对缸内流动及气门处的损失,且目前对于不同气门升程下进气性能研究较多,系统地对不同排气门升程下排气道流通能力的研究很少。目前柴油机正朝高增压、高喷油压力的方向发展[7-10],使得在相同排量的情况下,能够增大喷油量,提高功率密度。但对于高功率密度柴油机来说,循环进气量是制约功率提高的主要因素之一。循环进气量主要跟进排气道的流通能力有关,尤其当排气不畅时,会使排气过程缸压下降缓慢,增加活塞推出功,增加残余废气,进而影响下一循环的新鲜空气的充量。而排气门升程所形成的流通面积是排气道的实际进口面积,对排气道的流通能力有着重要影响。因此有必要对排气门升程进行优化,确定最大排气门升程的最优点,以提高排气道进气流通面积,降低排气流动阻力。本研究基于某柴油机的排气道,运用三维稳态CFD方法研究了排气门升程对排气道流通能力的影响规律,以期为最大排气门升程的设计提供理论指导。
1 研究方法及试验验证
鉴于稳流气道试验的高压差试验条件难以实现,本研究主要通过CFD仿真的方法进行排气门升程的研究。以实际排气道几何结构为基础,建立了排气道仿真模型(见图1),由于其对称性,为了节约计算时间,采用对称模型。
为了保证计算结果的准确性,需要对仿真模型进行校核和验证。首先,对网格独立性进行校核,建立基础尺寸为4 mm和6 mm的网格,并对气道网格进行细化。网格模型示意见图2。网格划分方案见表1。
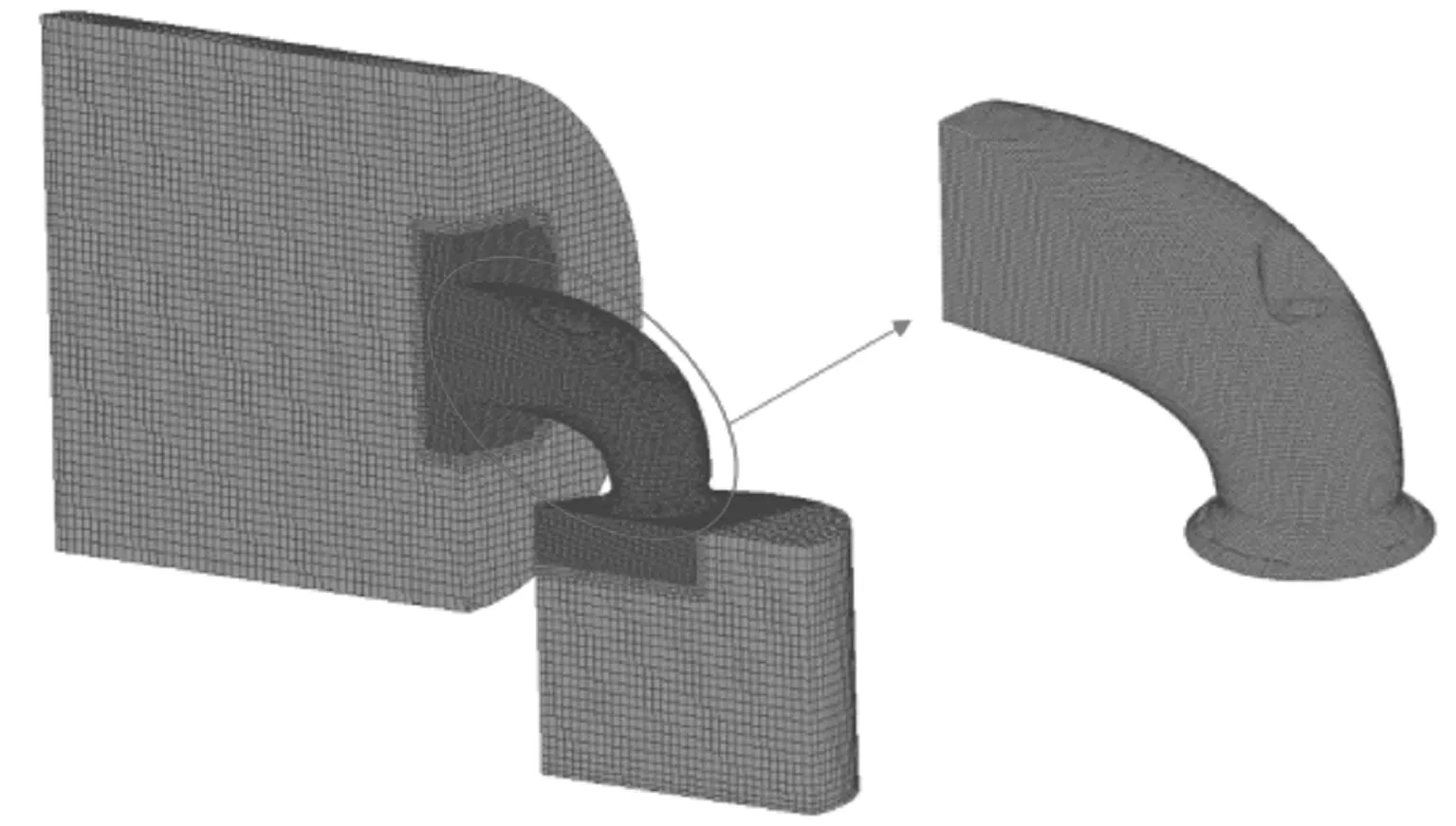
图2 排气道网格模型
表1排气道仿真模型网格划分方案
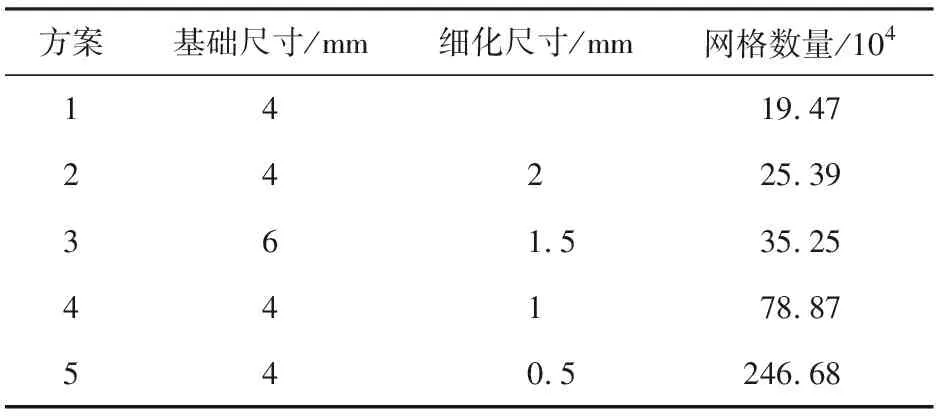
方案基础尺寸/mm细化尺寸/mm网格数量/10414 19.4724225.39361.535.2544178.87540.5246.68
固定排气门升程10 mm。进口设104.5 kPa总压,出口设101 kPa静压。图3示出排气道质量流量与计算时间随网格数的变化规律。可以看出,随着网格数增多,即网格尺寸减小,质量流量逐渐收敛。当网格数大于78.87万,即网格尺寸小于1 mm后质量流量开始收敛,此后变化很小,但计算时间大幅增长,综合考虑计算精度与时间,认为方案4最为合适。

图3 质量流量与计算时间随网格数的变化规律
利用稳流气道试验来评定和预测气道的流通特性,已成为内燃机领域的重要研究手段之一[11-13]。因此,通过稳流气道试验对排气道仿真模型进行验证。
取网格划分方案4的排气道仿真模型,采用压力边界条件,进口设总压,出口设静压;采用标准κ-ε湍流模型,近壁处采用标准壁面函数;收敛标准为10-4。
验证方案:固定排气门升程10 mm,计算不同压差下的排气道质量流量,并与相同工况下的试验结果进行对比,对比结果见表2。

表2 排气道仿真模型验证结果
从表2中可以看出,在相同压差时,仿真结果与试验结果误差均在3%以内。说明建立的排气道仿真模型是准确的,可以运用该排气道仿真模型进行拓展研究。
2 排气门升程对气道流通能力的影响规律
针对不同工况下排气门升程对气道流通能力的影响规律进行了研究。气道流通能力通常以流量系数为评价指标,流量系数=实际流量/理论流量,所以对流量系数进行定性分析。由于气体的可压缩性及本研究的高压差计算工况,理论流量的计算采用文献[14]提出的考虑气体压缩性的计算方法。
2.1 流量系数分析
可压理想状态的伯努利方程为
(1)
式中:vt为理论流速;p0为滞止压力;ρ0为滞止密度;k为绝热指数。
以理论流速衡量损失,可压实际状态的伯努利方程为
(2)
式中:va为实际流速;ε为总损失系数。
联立式(1)和式(2)可得
(3)
流量系数定义为在一定压差下,实际流量与理论流量的比值。对于同一气道的理想状态与实际状态而言,其出口处的面积相同,压力相同,因此出口密度相同,所以流量系数可以表示为
(4)
把式(4)代入式(3)可得
(5)
所以提高流量系数的关键在于减小气道内部的流动损失系数。
由文献[14]结果可知,气道出口面理论流速表达式为
(6)
定义相对压差
(7)
式中:pb为出口压力。
以相对压差为变量,出口面理论流速可表示为
(8)
对于滞止参数,满足理想气体状态方程
(9)
因为本研究的环境温度为常温,研究工况的滞止温度相同,因此
(10)
由式(8)和式(10)可知,出口面理论速度vt仅取决于相对压差。
损失系数既和气道结构参数有关,也和气体雷诺数有关[15]。对于相同结构的气道而言,雷诺数主要取决于气体的流速,即取决于相对压差。因此,可以预测在相同排气门升程及相同相对压差条件下,排气道的流量系数基本相同。
通过稳态CFD仿真计算了不同工况及排气门升程条件下的排气道流量系数,以验证预测结果的正确性。设无量纲参数排气门程径比(排气门升程与排气道进口直径之比,其中排气道进口直径为35 mm)Koh=ho/d来表征升程的大小。建立了不同排气门程径比的排气道仿真模型。
验证工况为排气背压100 kPa,200 kPa和300 kPa,相对压差为0.1和0.5,不同工况及排气门程径比条件下,排气道流量系数计算结果见图4。由图4可见,在相同排气门程径比及相同相对压差条件下,不同排气背压下的排气道流量系数基本相同,且最大偏差均小于1%,说明预测结果成立。所以后续对于排气门程径比的研究,可以仅以相对压差为参考。

图4 不同排气背压和相同相对压差下,排气道流量系数随排气门程径比的变化规律
2.2 排气道流量系数随排气门程径比的变化规律
内燃机排气过程包括自由排气和强制排气两个阶段,自由排气阶段排气门开启时,缸内平均压力一般为200~500 kPa[16],若不考虑排气背压因素,排气时的排气压差为100~400 kPa,即排气相对压差为0.5~0.8。自由排气结束后,气缸内的废气被上行活塞强制推出,直至排气门关闭,该过程为强制排气阶段,此时缸内平均压力高于排气管内平均压力约10 kPa,即排气相对压差为0.09。对空气而言,临界压比为0.528,即当相对压差为0.472时,排气道最小截面处将达到声速,此后随着相对压差的进一步增大,排气道理论质量流量不再增加,因此结合以上排气相对压差范围,取计算工况为相对压差0.09~0.5。不同相对压差条件下,排气道流量系数随排气门程径比的变化规律见图5。
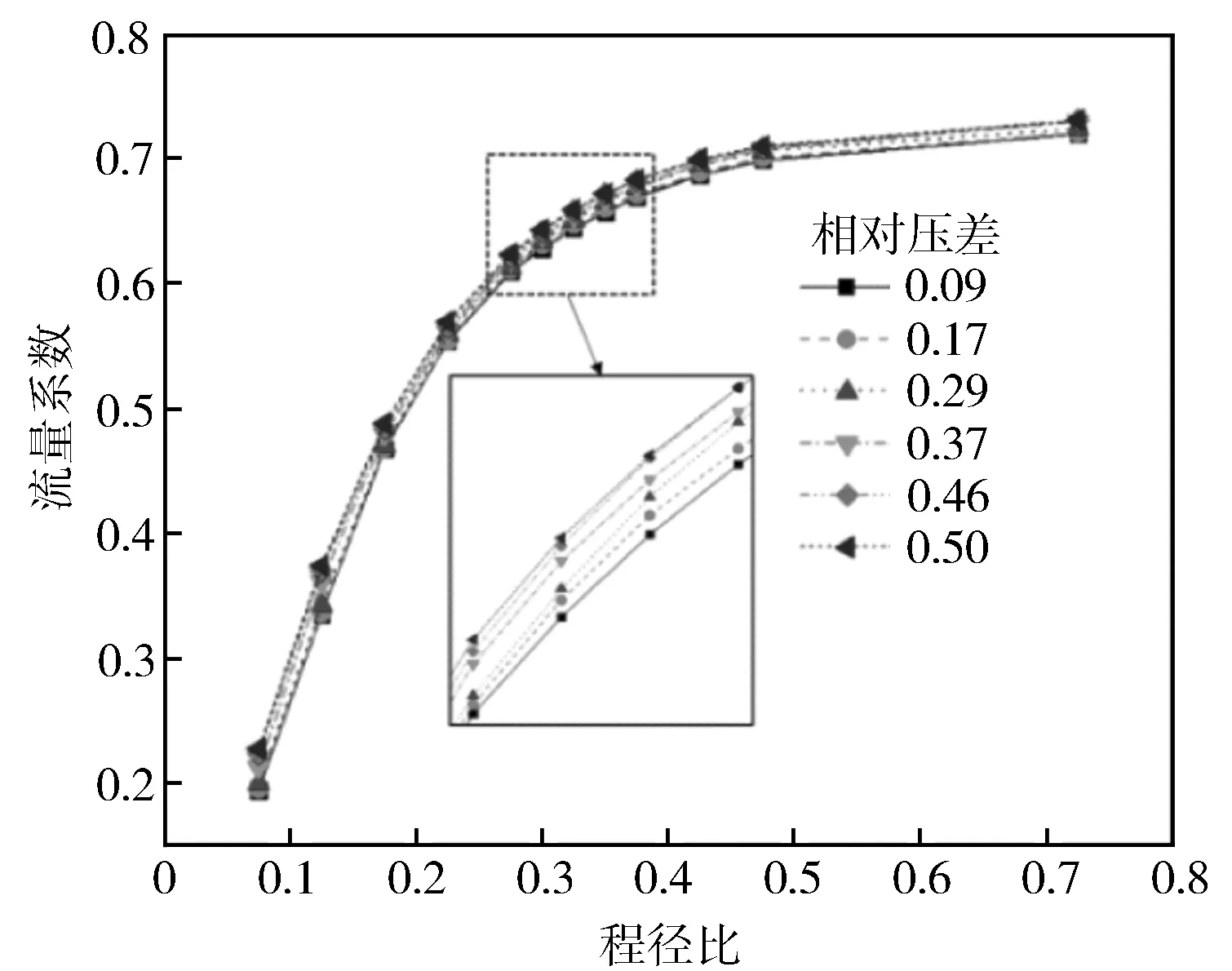
图5 不同工况下,排气道流量系数随排气门程径比的变化规律
由图5可见,在相同相对压差条件下,排气流量系数随排气门程径比的增大都呈现先快速增大然后增幅变缓的趋势;在相同排气门程径比条件下,排气道流量系数随相对压差的增大而增大。以图6所示的方式做切面,得到相对压差0.17,不同程径比下的总压云图(见图7)。

图6 排气道总压云图切面示意

图7 不同程径比下排气道内总压云图
在相同相对压差条件下,当排气门程径比很小时,缸内(气门前)为高压区,排气道内部(气门后)为低压区,压力梯度明显,说明气门处产生明显的节流效应,局部阻力损失明显。随着排气门程径比的增大,气门前后压力梯度逐渐减小,气门处的局部阻力损失减小,排气道流量系数增加。排气门开度所形成的流通面积Sh≈π·d·h,排气道进口面积Sin≈π·d2/4,当Sh>Sin,即Koh>0.25后,可以看出气门前后的压力梯度基本相同,说明当Koh>0.25后,气门处的节流损失已基本消失,此后流量系数的增幅开始变缓。排气道流量系数增幅变缓是因为排气道出口面积一定,本算例的压差一定,所以由文献[14]的理论流量计算公式可知,排气道的理论流量一定。由连续性方程ρvA=const可知,截面平均流速与截面面积总体呈倒数关系。排气门开度所形成的流通面积为排气道实际进口流通面积,由几何关系可知,随着排气门程径比的增大,排气道实际进口流通面积增加,所以排气道进口平均流速降低,流动阻力进一步减小,从而使流量系数进一步增加。进一步讲,排气门开度所形成的流通面积与排气门程径比成正比,进口流速又与进口面积成反比,因此进口流速也与排气门程径比成反比,随着排气门程径比的增大,进口流速减小,且减小幅度逐渐减小,所以流动阻力减小幅度减小,从而使流量系数增幅减小。总体而言,排气道流量系数随排气门程径比的增大先增大然后增幅逐渐变缓。
相关文献表明,在不同相对压差条件下,排气门处的突缩损失系数以及气道内部的流动损失系数均随流速的增大而减小[17],相对压差较大,流速较大,总损失系数较小,流量系数较大,所以在相同排气门程径比条件下,流量系数随相对压差的增大而增大。
定义因变量单位增量所对应的流量系数增长率为流量系数单位增长率,以下式计算:

(11)
式中:Δx为因变量的增量;Δc为Δx所对应的流量系数增量;c1为因变量增加之前的流量系数。
于本节而言,流量系数单位增长率的因变量为排气门程径比。工程上,10%以内的偏差即可满足工程精度要求,因此可以以流量系数单位增长率为10%的点所对应的排气门程径比为排气门程径比的费效比最佳点,即最佳排气门程径比。首先通过式(11)求得每个排气门程径比下的流量系数单位增长率,然后通过线性差值的方法对最佳排气门程径比进行计算。不同相对压差条件下,最佳排气门程径比见表3。

表3 不同相对压差下最佳排气门程径比
由表3可见,不同相对压差下的最佳排气门程径比基本不变,均在0.371~0.376之间,最大偏差1.35%,可以认为最佳排气门程径比不随相对压差的变化而改变。对其取平均,最佳排气门程径比为0.373。
由于结果是通过CFD仿真得到,具体数值不具有普适性,但排气道流通能力随排气门程径比的变化规律及最佳排气门程径比随相对压差的变化规律是通用的,所以可以提出最大排气门升程的设计方法:在对最大排气门升程进行设计时,选取发动机工作过程的任意相对压差,改变排气门程径比,对排气道流量系数进行计算,得到的流量系数随排气门程径比的费效比最佳点即为该发动机的最佳排气门程径比,结合排气道进口直径即可得到最佳的最大排气门升程。
3 结论
a) 排气道流量系数仅与损失系数有关,在相同的排气门程径比条件下,排气道流量系数仅取决于相对压差,即对于不同排气背压,若相对压差相同,则流量系数相同;
b) 在一定相对压差条件下,排气道流量系数随排气门程径比的增大而增大,但增幅逐渐变缓;在相同排气门程径比条件下,排气道流量系数随相对压差的增大而增大;
c) 最佳排气门程径比不随相对压差的变化而改变,以此提出最大排气门升程的设计方法:在对最大排气门升程进行设计时,选取发动机工作过程的任意相对压差,改变排气门程径比对排气道流量系数进行计算,得到的流量系数随排气门程径比的费效比最佳点即为该发动机的最佳排气门程径比,结合排气门直径即可得到最佳的最大排气门升程。
研究结果基于稳态仿真得到,后续可结合发动机实际工作过程,从瞬态角度进一步研究。
