新型湍流定容燃烧弹湍流场数值分析
2019-12-27秦思雨张欣王跃
秦思雨,张欣,王跃
(北京交通大学机械与电子控制工程学院,北京 100044)
环境污染与石油能源短缺已成为世界各国当前亟待解决的两个问题,在应对上述问题上,气体燃料具备很大的潜力和广阔的应用前景[1]。目前气体燃料发动机的相关理论尚未完全成熟,主要依靠试验的方法进行研究[2]。
由于发动机实际工作过程相对复杂,各循环间存在较大变动,很难限制每个工作循环中各项控制参数不变,试验结果的对比性不强,因此发动机燃烧机理的研究通常在模拟燃烧装置中进行[3]。定容燃烧弹作为发动机模拟燃烧装置,主要模拟发动机活塞位于上止点附近时发动机气缸内定容燃烧情况,可用于研究燃烧环境参数、燃空当量比等单一参数变化对发动机缸内燃烧压力、火焰传播等相关特性的影响,可为发动机关键技术的研发提供重要的试验数据[4]。定容燃烧弹试验装置因其结构简单、操作方便、燃烧过程火焰图像可视化、试验可重复性强等优点广泛地应用于湍流燃烧试验研究中[5]。
发动机燃烧室内的湍流强度能够影响气体燃料混合特性以及燃烧特性,合理营造燃烧室内湍流环境是提高发动机效率的关键所在[6]。因此,设计了一种新型容弹内湍流发生系统,在容弹内部产生持续可调控的各向均匀对称湍流环境,用于湍流燃烧试验研究。对湍流定容燃烧弹内部流场进行数值模拟,并对计算结果进行分析,辅助湍流定容燃烧弹试验系统的设计。
1 定容燃烧弹及湍流发生系统设计方案
1.1 定容燃烧弹
为保证容弹内部湍流流场的均匀对称特性,定容燃烧弹为对称结构,定容燃烧弹弹体近似为球体。容弹的弹体内腔直径为200 mm,内腔容积为6.38 L,弹体前后两个方向留出直径为100 mm圆柱空腔,与高透石英玻璃相配合,作为高速摄影纹影光路的通路;为保证容弹弹体完全对称,在其余4个方向也留出100 mm的圆柱空腔。在容弹弹体上对称加工8个直径为12 mm的气体入口通道,用于连接分流后的气体管道。
1.2 湍流发生系统
纵观国内外学者用于湍流燃烧试验研究所采用的容弹内湍流发生系统,根据产生湍流的原理,主要分为孔板平动式[7-8]、进气射流式[9]、旋转扰动式[10-11]、复合式四类[12]。
本研究设计的湍流发生系统采用进气射流式结合射流碰撞的方法来营造各向均匀对称湍流环境。湍流发生系统主要由电动机、变频器、同步联轴器、单缸发动机、气体管路以及分流腔组成,定容燃烧弹及湍流发生系统的示意见图1。湍流发生系统产生可调控的各向均匀对称湍流环境的原理如下:由一个双轴伸电动机通过联轴器同时倒拖带动两个单缸发动机活塞作往复运动,活塞往复运动带动发动机燃烧室、气体管路以及容弹内腔的气体流动。由于单个电动机通过联轴器与发动机刚性连接,可以保证电动机在带动活塞运动过程中2台发动机的活塞位置完全同步;容弹本身结构上对称,且由于气体管路以及分流腔、容弹弹体上气体管路入口的布置完全对称,故而气体通过入口进入容弹时的速度相同,气体经由8个对称分布的入口以气体射流形式在容弹中心位置相互碰撞,形成各向相对均匀对称湍流环境。通过变频器可以调节驱动电动机的转速,进而改变发动机的转速以及活塞运动规律,从而控制容弹内部的湍流环境特征参数。
2 内部流场数值模拟求解方法
2.1 基本方程与湍流模型
流体流动要遵循物理守恒定律,其基本的守恒方程包括质量守恒、动量守恒及能量守恒方程。
质量守恒方程:
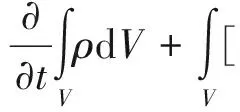
(1)
式中:t为时间;ρ为流体密度;V为流体微元的体积;u为速度向量。
动量守恒方程:
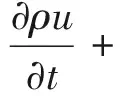
(2)
式中:g为重力加速度;λ为系数;η为流体动力黏度。
能量守恒方程:

(3)
式中:Cp为比定压热容;T为流体温度;k为热传导系数;Q为能量源。
在湍流模型方面,本研究选取了Realizableκ-ε模型,Realizableκ-ε模型在圆口射流模拟中能给出较好的射流扩张角。Realizableκ-ε模型的湍动能及耗散率输运方程为
(4)
(5)
式中:κ为湍动能;ε为耗散率;Gκ为由于平均速度梯度引起的湍动能;Gb为由于浮力影响引起的湍动能;YM为可压缩湍流脉动膨胀对总耗散率的影响;μt为湍流黏性系数。
湍流强度定义为脉动速度分量的均方根值,针对容弹中心点的湍流强度,本研究模拟以及试验的湍流强度数据处理均采用时间平均法计算湍流强度,计算公式为
(6)
(7)
(8)
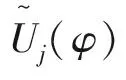
对于湍流强度场的分布计算,鉴于计算成本与后处理的时间成本,采用经验公式通过湍动能来计算,其计算的经验公式为
(9)
2.2 模型简化及网格划分
在湍流发生系统工作过程中,在单缸发动机的燃烧室、气体管路、分流腔以及容弹内腔这些区域内存在流体流动,故而简化湍流发生系统及容弹的模型(见图2)。

图2 湍流定容燃烧弹计算域简化模型
本研究选取ANSYS ICEM网格划分软件对简化模型进行网格划分,采用结构化网格与分结构化网格相结合的混合网格。单缸机燃烧室以及气体管路总管形状相对规则,故采用结构化网格划分方法;容弹内部、分流腔以及分流细管结构相对复杂,采用非结构化网格划分方法。简化模型采用混合网格划分方法完成划分,总网格数量为1 078 049个,最小网格尺寸0.015 mm3,最小网格质量为0.40。
2.3 动网格及求解设置
因为要模拟湍流发生系统工作中活塞的往复式运动,需要对数值模拟模型进行动网格设置。发动机活塞部分采用结构化网格划分,因其运动幅度较大,故采用铺层法进行动网格设置。活塞运动规律采用In-cylinder模型控制,铺层法的分离因子αs和合并因子αc都设为0.1,将定容弹两侧的发动机活塞顶表面指定为刚体,并将活塞运动规律曲线赋予活塞顶表面,定义定容弹左侧发动机活塞起始运动方向为x轴负方向,右侧发动机活塞起始运动方向为x轴正方向。活塞运动规律计算公式如下:
(10)
式中:θc为曲柄角,θc=t×n;Ps为活塞位移;L为连杆长度;A为活塞行程。
生成的发动机活塞动网格随曲轴转角的变化见图3。

图3 基于铺层法建立的发动机活塞动网格
Fluent软件带有两种求解方法:压力基求解器和密度基求解器。本研究选取压力基求解器,压力修正方法采用PISO算法。简化模型初始压力设置为0.1 MPa,初始温度为298 K。弹体表面、气体管道、分流腔表面设置为非绝热壁面边界条件。对流动、湍动能和湍流耗散率等的离散格式采用二阶迎风格式。
计算步长为发动机曲轴旋转1°所需时间,每迭代计算20次为1°曲轴转角,计算步长的具体时间长度根据动网格设置的发动机转速不同而改变,以2 000 r/min为例,其计算步长为0.083 3 ms,总计算步数为30万。在模拟计算中发动机开始运转后8 s以上计算结果收敛,容弹内部流场达到相对稳定时的状态,本文的计算结果全是在以上条件下得到的计算结果。
3 计算结果及分析
3.1 系统内部流场模拟结果及分析
设置In-cylinder模型控制的发动机转速为2 000 r/min,对湍流发生系统及容弹内部流场的数值模拟结果进行了分析,通过对系统内部流场分布规律进行分析,辅助指导湍流发生系统的设计。
在以下描述中,以发动机曲轴旋转360°为一个循环,因为本研究中发动机仅作为带动容弹内部空气流动作用,类似于压气机,不同于传统发动机。以活塞处于上止点位置时刻作为一个循环的起始,记此时的曲轴转角为0°。
3.1.1入口速度分布规律
湍流发生系统设计方案中,依靠2个发动机活塞运动规律相同,再通过气体管路的布置对称以及容弹内部结构对称实现在气体通过入口进入容弹时的速度相同,以便对称的射流在容弹中心处碰撞形成空间上均匀对称的湍流环境,故而入口处气流速度的大小与变化规律对形成均匀对称湍流环境尤为重要,是形成均匀对称湍流环境的基础,速度大小与容弹内湍流的大小也有着密切联系。
在数值模拟过程中,在容弹的8个气体入口中心处设置监测点,监测该点在一个循环内的速度变化规律。8个入口中心点的气流速度变化规律见图4。起始时刻0°曲轴转角为活塞位于上止点位置时刻。
从图中可以看出,在转速设为2 000 r/min时,入口速度出现两次峰值,速度曲线的两次极小值之间相隔约180°曲轴转角,这是因为容弹系统内部的气体流动是由发动机活塞往复运动引起的,其速度变化规律与发动机活塞运动速度密切相关。入口速度在200°曲轴转角时最小,最小值为4.2 m/s,在300°曲轴转角左右达到最大,最大值为80.4 m/s;入口速度最大值与最小值出现位置并不在270°曲轴转角与180°曲轴转角左右,这是因为随着转速的不同,气体在管路中的流动速度不同,到达入口处的时间不同,入口速度与活塞运动速度存在着不同程度的滞后。在一个循环内,任意时刻8个入口的速度基本相同,在120°曲轴转角左右出现最大差值,最大差值为2.23 m/s,误差在3.43%左右,整体变化规律趋势吻合较好,保证了形成均匀对称湍流环境的基础条件。
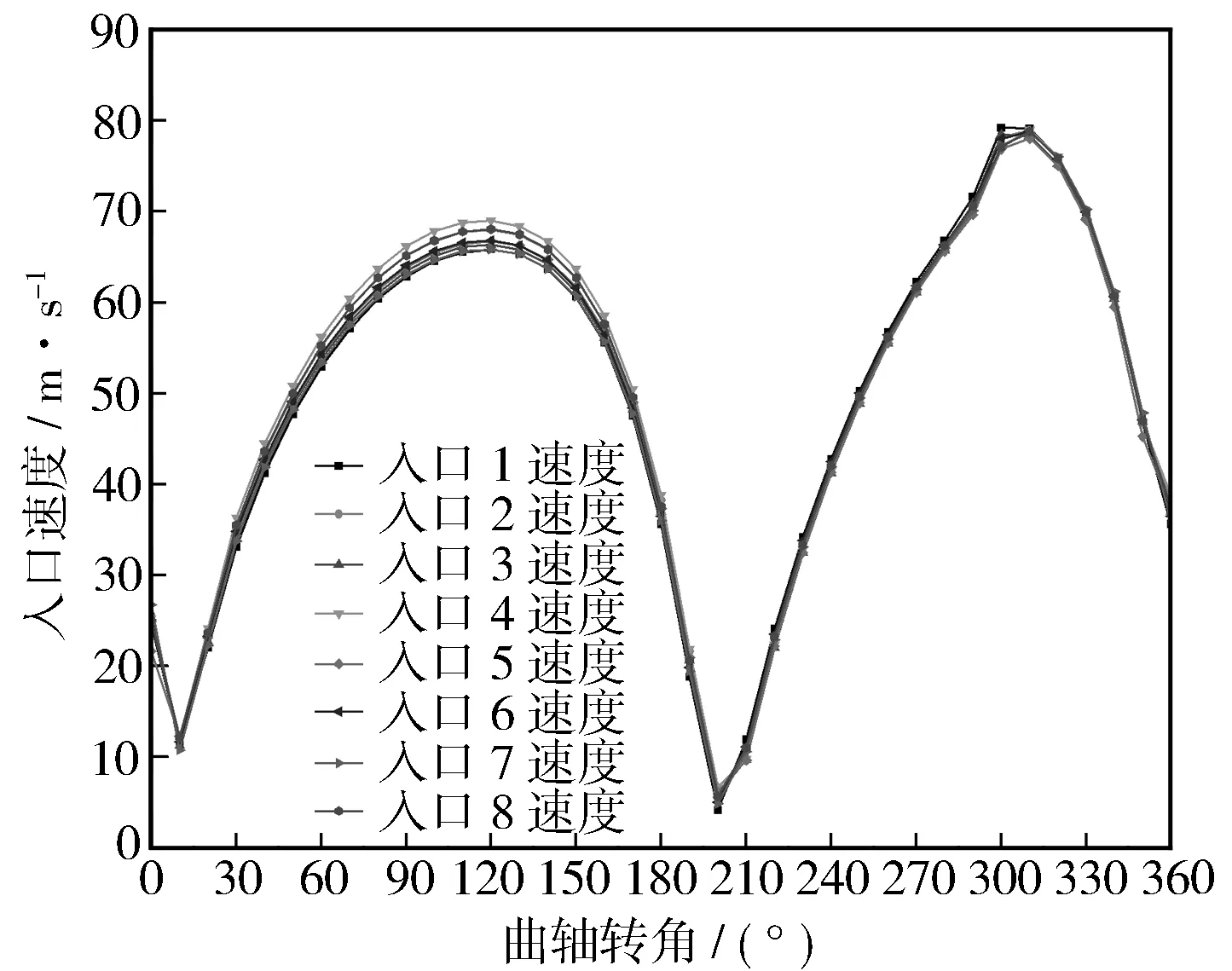
图4 单个循环内8个入口气体速度变化对比
3.1.2湍流分布规律

当活塞位于上止点0°曲轴转角时,过容弹中心点XY,YZ截面的湍流场见图5。从图中可以看出,XY,YZ截面湍流强度分布规律与大小分布基本一致,空间上距中心点距离相同位置处湍流强度差值在0.2 m/s以下,即距中心点距离相同位置处各个方向上的湍流强度基本相同。湍流强度在空间上呈
中心对称且分层分布的特点,湍流强度从中心到外围球形圈逐渐减小,在中心处湍流强度最大,最大值为9.8 m/s,在中心半径约为50 mm的圆形区域内,湍流强度分布都在7.2 m/s以上。在实际试验过程中,用于拍摄的透明玻璃光路的半径为50 mm,但由于容弹内径为100mm,可用于火焰传播特性参数研究的直径约为30 mm,即湍流强度分布在7.7~9.8 m/s的区域内。在容弹内部,距离中心点相同位置处在X,Y,Z3个方向上的湍流强度基本相同,湍流强度整体分布呈由中心分层递减的特征,符合湍流发生系统的设计初衷。

图5 容弹内部湍流场分布云图
3.1.3湍动能分布规律
当活塞位于上止点180°时,过容弹中心点的XY,YZ截面的湍动能分布云图见图6。从图中可以看出,容弹内部的湍动能场在XY,YZ截面都呈现出均匀对称的分层式分布特点,从中心位置到外围扩散湍动能逐层减小,在不同方向上且距离中心点相同的位置点处湍动能基本相同。在中心位置最大湍动能达到145 m2/s2,在半径30 mm的圆形区域内湍动能分布在90~145 m2/s2。由于气体通过入口进入容弹时的速度相同,8个入口对称分布的气体射流在容弹中心位置相互碰撞,在容弹内部形成了均匀对称的湍流场。
3.2 电机转速对系统内部流场的影响
在试验过程中,需要营造不同特征参数的湍流环境以满足不同条件下的试验要求。故在湍流发生系统的设计方案中,设置了电动机的变频器,通过调节变频器的输出频率控制电机转速,从而带动活塞以不同的运动规律往复运动,实现容弹内部湍流环境的可控调节。模拟计算了电动机转速在1 000 r/min,1 500 r/min,2 000 r/min情况下容弹内部的流场分布,对比分析不同电动机转速下容弹内部的流场分布规律。
3.2.1电机转速对入口速度的影响
不同电动机转速下,一个循环内入口速度的变化规律见图7。起始时刻0°曲轴转角为活塞位于上止点位置时刻。从图中可以看出,当电动机转速为1 000 r/min时,入口速度在170°曲轴转角时最小,最小值为0.6 m/s,在300°曲轴转角左右达到最大,最大值为30.0 m/s;当电机转速为1 500 r/min时,入口速度在180°曲轴转角时最小,最小值为1.6 m/s,在300°曲轴转角左右达到最大,最大值为43.7 m/s;当电动机转速为2 000 r/min时,入口速度在210°曲轴转角时最小,最小值为4.2 m/s,在310°曲轴转角左右达到最大,最大值为80.4 m/s。随着电动机转速的升高,入口处的最大速度随之升高。电机转速1 000 r/min时一个循环内平均速度为15.5 m/s,电机转速1 500 r/min时一个循环内平均速度为27.6 m/s,电机转速为2 000 r/min时一个循环内平均速度为49.9 m/s,随着电机转速的提高,整体平均速度也得到了提升。另外在不同电动机转速情况下,速度最大值以及最小值出现的相位也发生了变化,这是因为当活塞运动到下止点位置时,由于气体的运动具有惯性,继续由容弹内部流向气缸,随后活塞运动方向发生突变,带动气体由气缸流向容弹内部,在入口处两种方向的气体相互碰撞,由于电机转速越大的情况下活塞到达下止点位置时的入口气流速度越大,故而气体流动方向改变时(即最小速度出现相位)的相位相对更为滞后。

图7 不同电动机转速情况下入口速度变化规律
3.2.2电机转速对湍流强度的影响
在不同电动机转速下,容弹中心位置处一个循环内湍流强度变化见图8。曲轴转角起始时刻0°为活塞位于上止点位置时刻。从图中可知,随着电机转速的升高,一个循环内容弹中心位置的湍流强度整体明显提升。在电动机转速为1 000 r/min时,湍流强度在220°曲轴转角左右时最小,最小值为0.4 m/s,在310°曲轴转角达到最大,最大值为6.0 m/s,上止点0°曲轴转角时的湍流强度为4.6 m/s;在电动机转速为1 500 r/min时,湍流强度在270°曲轴转角左右时最小,最小值为0.5 m/s,在350°曲轴转角时达到最大,最大值为8.2 m/s,上止点0°曲轴转角时湍流强度为7.7 m/s;在电动机转速为2 000 r/min时,湍流强度在310°曲轴转角左右时最小,最小值为1.3 m/s,在20°曲轴转角达到最大,最大值为10.3 m/s,上止点0°曲轴转角时湍流强度为9.8 m/s。在实际试验过程中,在活塞位于上止点时,随着电动机转速的升高,容弹中心位置的湍流强度也随之升高。所以通过调节电动机的转速可以调控容弹内部湍流强度,符合湍流发生系统设计方案中容弹内部湍流环境可调控的设计初衷。

图8 不同电动机转速下容弹中心湍流强度变化规律
4 数值模拟与试验结果对比分析
在试验过程中,运用热线风速仪测量计算了容弹中心位置处的湍流强度,在不同电动机转速情况下,数值模拟计算得到的湍流强度结果与试验测量计算得到的湍流强度结果对比见图9。
从图中可以看出,在电机转速为1 000 r/min时,纵观一个循环,模拟与试验得到的湍流强度变化趋势相吻合,模拟结果湍流强度的最小值出现在220°曲轴转角,最小值为0.4 m/s,试验结果湍流强度的最小值出现在230°曲轴转角,最小值为0.26 m/s;模拟结果的湍流强度最大值出现在310°曲轴转角,最大值为6.0 m/s,试验结果湍流强度的最大值出现在280°曲轴转角,最大值为5.8 m/s。
在电机转速为1 500 r/min时,纵观一个循环,模拟与试验结果湍流强度变化趋势相吻合,模拟结果的湍流强度最小值出现在270°曲轴转角,最小值为0.5 m/s,试验结果湍流强度的最小值出现在290°曲轴转角,最小值为0.45 m/s;模拟结果湍流强度的最大值出现在350°曲轴转角,最大值为8.2 m/s,试验结果湍流强度的最大值出现在310°曲轴转角,最大值为8.37 m/s。
在电机转速为2 000 r/min时,纵观一个循环,模拟与试验结果湍流强度变化趋势相吻合,模拟结果湍流强度的最小值出现在310°曲轴转角,最小值为1.3 m/s,试验结果湍流强度的最小值出现在330°曲轴转角,最小值为1.23 m/s;模拟结果湍流强度的最大值出现在10°曲轴转角,最大值为10.2 m/s,试验结果湍流强度的最大值出现在360°曲轴转角,最大值为10.44 m/s。
由于试验过程中存在循环变动,仍存在部分模拟结果和试验结果一致性较差工况点,但模拟与试验的结果在整体上有着良好的一致性,验证了所建立模型的准确性。

图9 试验与模拟湍流强度结果对比
5 结束语
本研究基于Fluent软件对一种新型湍流发生系统以及容弹内部流场进行了数值模拟,对湍流发生系统以及容弹内部流场数值模拟结果进行了分析,佐证了最初设计方案的可行性,最后用试验数据验证了模型的准确性。
对于设计的湍流发生系统,容弹的8个气体入口气体速度基本一致,容弹内部的湍流强度与湍动能场呈现出均匀对称的分层式分布特点,湍流强度及湍动能从中心位置到外围逐层减小,在不同方向上,距离中心点相同位置处的湍流强度与湍动能基本相同,结果表明:湍流发生系统设计方案可以实现在容弹内部产生均匀对称湍流环境的设计要求。
调节电机转速可以改变容弹入口处的气流速度,从而改变容弹内部湍流强度大小。随着电机转速的升高,容弹内部湍流强度整体呈升高趋势,故而通过变频器调节电动机转速可以实现容弹内部湍流环境可调控的设计初衷。
