增压器涡轮端热边界对流场仿真的影响
2019-12-27尹川川倪计民金文华
尹川川,倪计民,金文华
(同济大学汽车学院,上海 201804)
随着发动机动力性、经济性的不断提高和排放标准的日益严格,涡轮增压器的转速和增压比不断提高,热负荷和机械负荷不断增大,对其耐久性的要求也越来越高。涡轮增压器涡轮端包含蜗壳、废气旁通阀、涡轮,其能否持续可靠工作是衡量涡轮增压器耐久性的重要判据之一[1-2]。研究表明,热应力过大造成的塑性应变是引起热机械疲劳的主要失效机制,因此,热应力研究是当前涡轮端结构设计的重要工作。而热应力计算要以准确获取涡轮端温度分布为前提,通过研究涡轮端结构的温度分布和应力应变分布可及时有效地发现结构中可能发生热裂纹的部位,对涡轮端结构的设计和优化具有重要意义。以往学者处理涡轮端高温废气的流动与传热多采用单向耦合法[3-6],即预先将涡流道内壁面作绝热处理,将求得的废气与壁面交界处的温度作为固体传热边界条件进行涡轮端温度场计算,这与真实传热情况存在一定偏差。
本研究将发生在涡轮增压器涡轮端的热传导与高温废气的对流换热耦合起来,直接求解,并设计试验进行验证。同时试验部分针对涡轮端各测点开展了涡轮端瞬态温度变化研究,以及不同进气条件对涡轮端温度影响的探究试验,以获得准确的涡轮端温度场,为计算涡轮端耐久性提供前提条件。
1 数值模拟基础理论
1.1 计算流体动力学控制方程
对涡轮端结构开展的传热仿真计算需要涉及涡轮端流体流动及传热的求解,涡轮端的流体域为发动机排气从涡轮端入口途经涡轮到涡轮端出口的全部流道。
1.1.1控制方程
质量守恒方程、动量守恒方程和能量守恒方程组成了流体力学的基本方程,也是计算流体力学的控制方程[7-8]。
质量守恒方程:
(1)

动量守恒方程[7-8]:
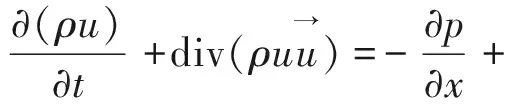
(2)
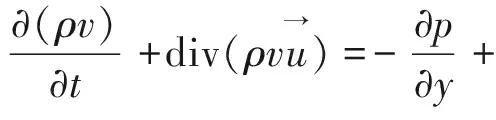
(3)

(4)
式中:μ为动力黏度;SMx,SMy,SMz为动量守恒方程的广义源项;p为压力。
能量守恒方程[7-8]:
(5)
式中:cp为比热容;T为温度;h为流体传热系数;ST为黏性耗散项,代表在流体内热源以及流体的黏性作用下,机械能转换为热量的部分。
1.1.2涡轮端流体域求解模型
发动机排气在涡轮端的流动速度非常高,呈现为复杂的湍流流动状态。针对涡轮端流体域的流动计算,本研究采用标准κ-ε模型:

(6)
(7)
式中:Gκ为平均速度梯度引起的湍动能项;Gb为浮力引起的湍动能项;YM为在可压缩湍流中脉动扩张对于整体耗散率的贡献;C1ε,C2ε和C3ε为经验常数,通常C1ε=1.44,C2ε=1.92 ,C3ε在流体流动方向与重力方向平行时为1,流体流动方向与重力方向垂直时则为0;σκ及σε为κ和ε的湍流Prandtl数,一般取σκ=1.0,σε=1.3;Sκ和Sε为用户自定义的源项,通常Sκ=0,Sε=0[8-9]。
1.2 涡轮端传热求解模型
涡轮端传热的热源为进入涡流道的发动机排气。涡轮端热量传递包含固体域的热传导、废气经涡轮通道膨胀做功的功热转换、流固交界面的共轭传热以及热辐射,本研究暂不考虑热辐射。涡轮端气体流道与涡轮叶片的交界面、气体流道与涡流道内壁面的交界面这两处热量传递为流固交界面共轭传热(见式(8)和式(9)),联立牛顿冷却公式及傅里叶定律可求得交界面处的表面传热系数[10-11](见式(10)、式(11))。
qf=qs,
(8)
ts=tf,
(9)

(10)
(11)
热传导发生部位在涡轮端结构内部,蜗壳的材料为D-5S。导热方程为
(12)
式中:ρ,c,t,τ,φ分别为各微元体的密度、比热容、温度、时间和内热源生成热 。
本研究热传导满足第三类边界条件,空气温度取环境温度。
2 涡轮端传热模型和热边界条件
2.1 研究对象
整机的三维模型见图1,废气旁通阀会在高负荷下入口排气压力过高时开启。该系列增压器匹配的发动机标定功率范围在92~132 kW。
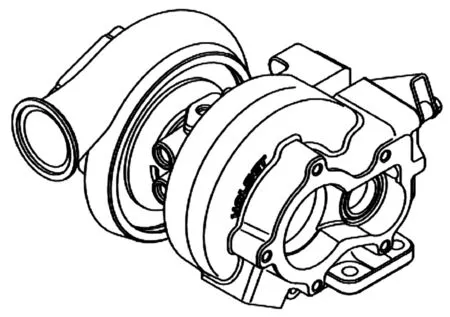
图1 涡轮增压器实物图
2.2 三维模型
涡轮端固体域三维模型见图2,对固体域布尔求差得到流体域(见图3)。110 000 r/min 工况下,废气旁通阀开启,流体域基于开启旁通阀后的增压器涡轮端三维模型重新提取。
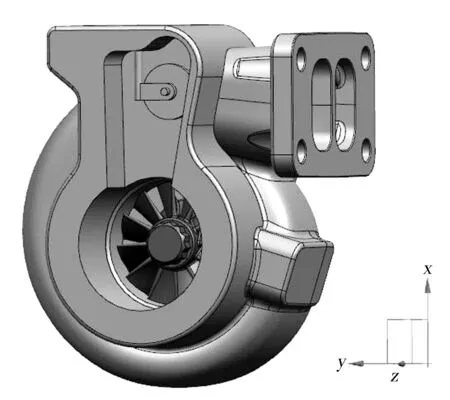
图2 涡轮端几何模型

图3 流体域
2.3 网格生成
利用Ansys Meshing软件来生成网格。对涡轮端固体域采用全四面体作网格划分,基于计算精度和计算量的考虑,设定单元网格的基本尺寸为2 mm,网格数为1 436 582;将流体域几何划分为三部分:涡轮端涡流道进口段、涡轮端叶轮流道、涡轮端旁通通道及出口段(设为三段的目的是为了便于设置3种热边界条件)。为加快计算过程的收敛,对涡流道进口和出口段作了适当的延长处理,其中延长部分结构简单,采用六面体网格;涡轮端涡流道进口段、叶轮流道、涡轮端旁通通道及出口段因为流道结构复杂,采用四面体非结构化网格;对于各区域流道近壁面区域,单独划分边界层网格,层数设为5,增长率为1.2,调整网格密度,使其第一层网格节点布置在对数律层,y+值落在30~300区间内。流体域网格数量见表1。

表1 流体域网格数量
2.4 边界条件设置
选用CFX作为求解器;流体域的工质设为理想气体;参考压力为0.1 MPa,压力为表压。热量传输模型选用全热模型(Total Energy),该模型在原有的热焓基础上,还额外考虑流体自身因流动引起的热量变化,对高速流体及可压缩流体的热量传输计算适应性较好。涡轮端叶轮流道内的流体域设为旋转域,旋转速度由不同工况下的台架实测转速给出,涡轮端涡流道进口段和旁通通道以及出口段所在的流体域设为静止域。本算例在流动计算模型上选用满足绝大多数工程计算要求的κ-ε模型。入口边界条件包括增压器涡轮端进气质量流量和进气温度,均由增压器试验台架实测数据给出,各工况下的入口边界条件见表2。涡轮增压器涡轮端流体和固体壁面发生热量交换的地方有叶轮表面和涡轮端涡流道内壁面两处(见图4)。设置3种不同的热边界条件,模型1的热边界条件是全部壁面绝热(叶轮表面和涡流道内壁面),模型2的热边界条件是仅叶轮表面共轭传热(涡流道内壁面绝热),模型3的热边界条件是全部壁面共轭传热(叶轮表面和涡流道内壁面)。对于固体域,涡轮端外壁面与外界空气存在自然对流传热,取自然对流传热系数为10 W/(m2·K) 。外界空气温度取增压器试验台架所处的环境温度。
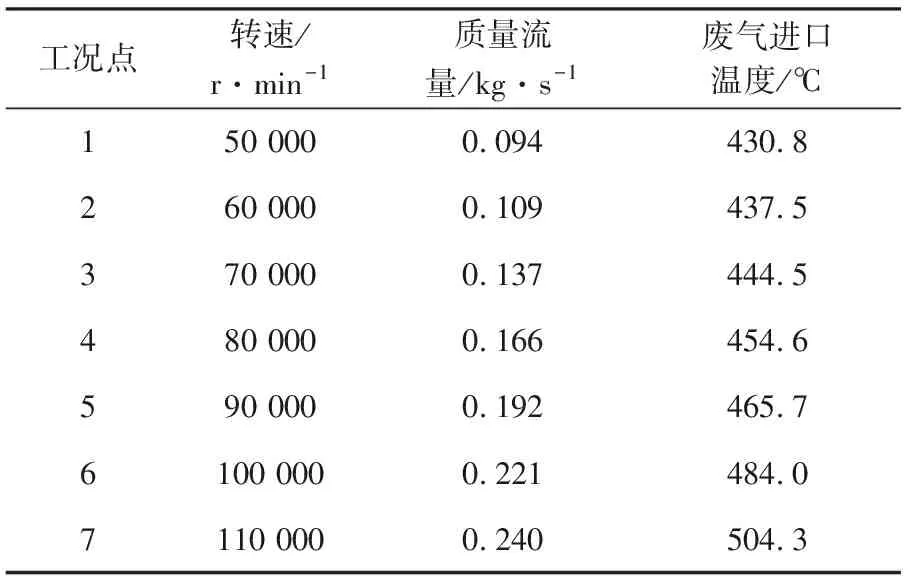
表2 仿真计算工况点入口边界条件
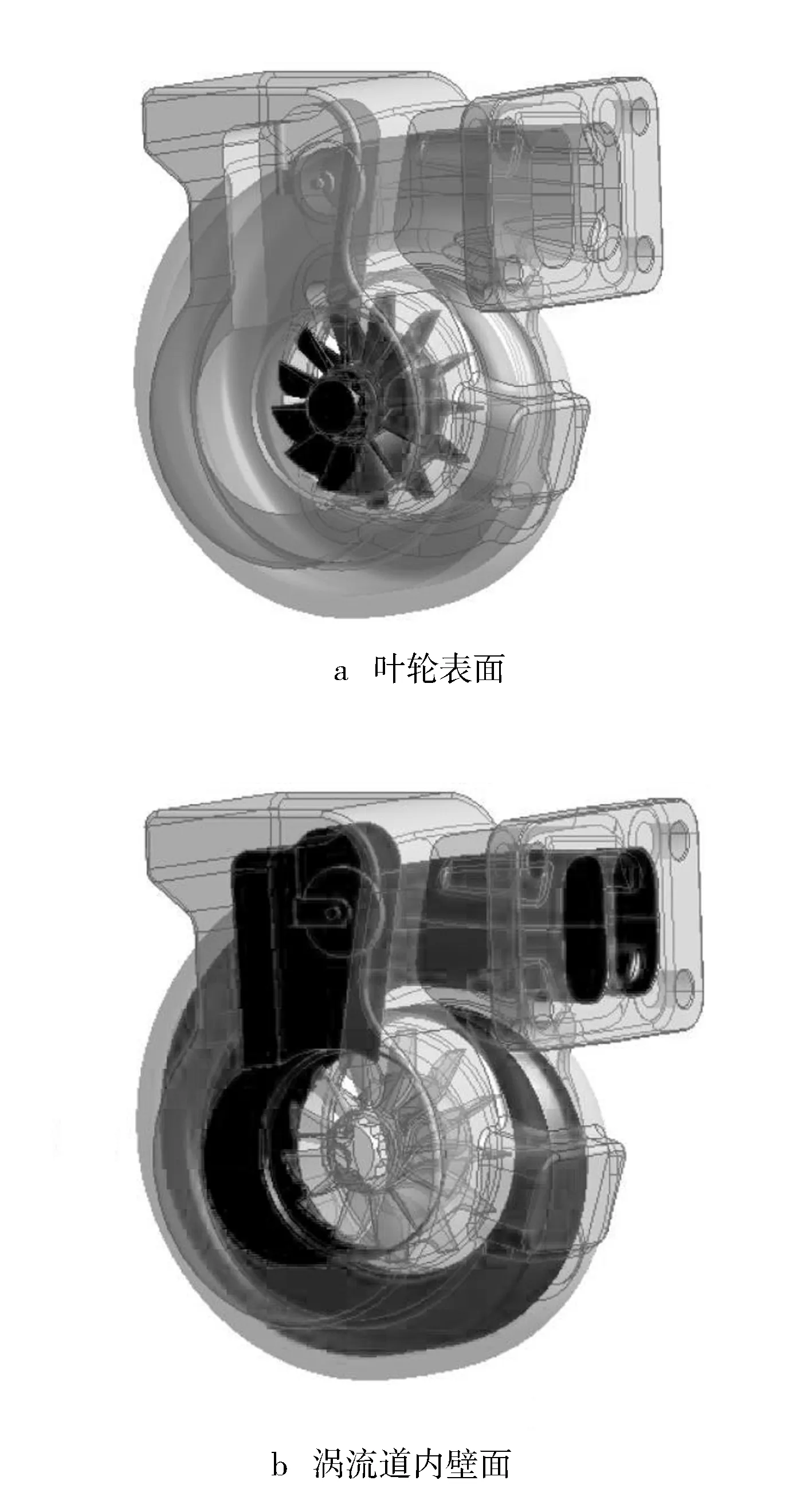
图4 涡轮端换热壁面
3 不同热边界条件下的计算结果
3.1 对流场温度分布的影响
图5示出50 000 r/min工况下,模型1、模型2和模型3对应涡轮端流场xy截面温度分布和叶轮表面温度分布。

图5 50 000 r/min工况涡轮端流场xy截面温度与叶轮表面温度
由图5可以看出,同一工况下,热边界条件虽有差异,但整体温度分布相同,都沿气体流动方向降低。涡轮端叶轮是将热能转为机械能的重要部件,如图5a虚线圈所示,叶轮流道进口及稍后一段,黑色饱和度变化最明显,说明高温废气的焓降最明显,温降最显著。图5a虚线矩形中所示气体流经涡流喉口进入叶轮流道时,部分气体因无法贴紧壁面产生漩涡,导致局部温度升高,这在3个模型中都得到了较好呈现。从数值上看,3种模型最高温度相同,为430.8 ℃,最低温度分别为339.8 ℃,335.4 ℃,317.4 ℃,涡流道进口段温降分别为22.7 ℃,26.4 ℃和45.3 ℃。原因是高温废气在流体域与涡流道内壁面发生共轭传热,在自身膨胀温度降低的同时,废气和涡流道内壁对流传热,导致温降差异较大。图6示出基于不同热边界条件模型计算得到的废气在增压器涡轮端产生的温降随转速的变化关系。

图6 废气在涡轮端的温度随转速变化关系
随着增压器转速上升,废气膨胀做功不断增加,进气质量流量增加,涡轮端进出口温差扩大。流固耦合界面为共轭传热边界条件的模型涡轮端进出口温降明显高于绝热边界计算所得温度降,尤其在50 000 r/min工况下,温降差异明显,达到25.4 ℃,说明热边界准确性对于涡轮端温度场计算的重要性。值得注意的是,增压器转速达到110 000 r/min以上时,废气旁通阀处于开启状态,废气未经叶轮流道膨胀直接流向涡轮下游,3个模型废气经过涡轮端温降为64.6~74.3 ℃。图7和图8分别示出100 000 r/min和110 000 r/min下涡轮端xz截面的温度分布。旁通阀开启时,如图8虚线矩形所示,温度场在旁通阀附近分布复杂,气体从开启的旁通阀两端的狭小通道加速流过,温度呈现下降趋势;旁通阀附近流道拐角处,因为存在漩涡,气体流速降低,产生不可逆损失,使得温度上升。如图8虚线圆所示,在旁通阀出口处,未参与膨胀做功的气体温度明显高于经过叶轮做功的气体温度。同时,从废气旁通阀流出的气体因为存在横向速度,使得叶轮出口流出废气受到挤压,低温区呈现向远离旁通阀流道压缩的趋势。
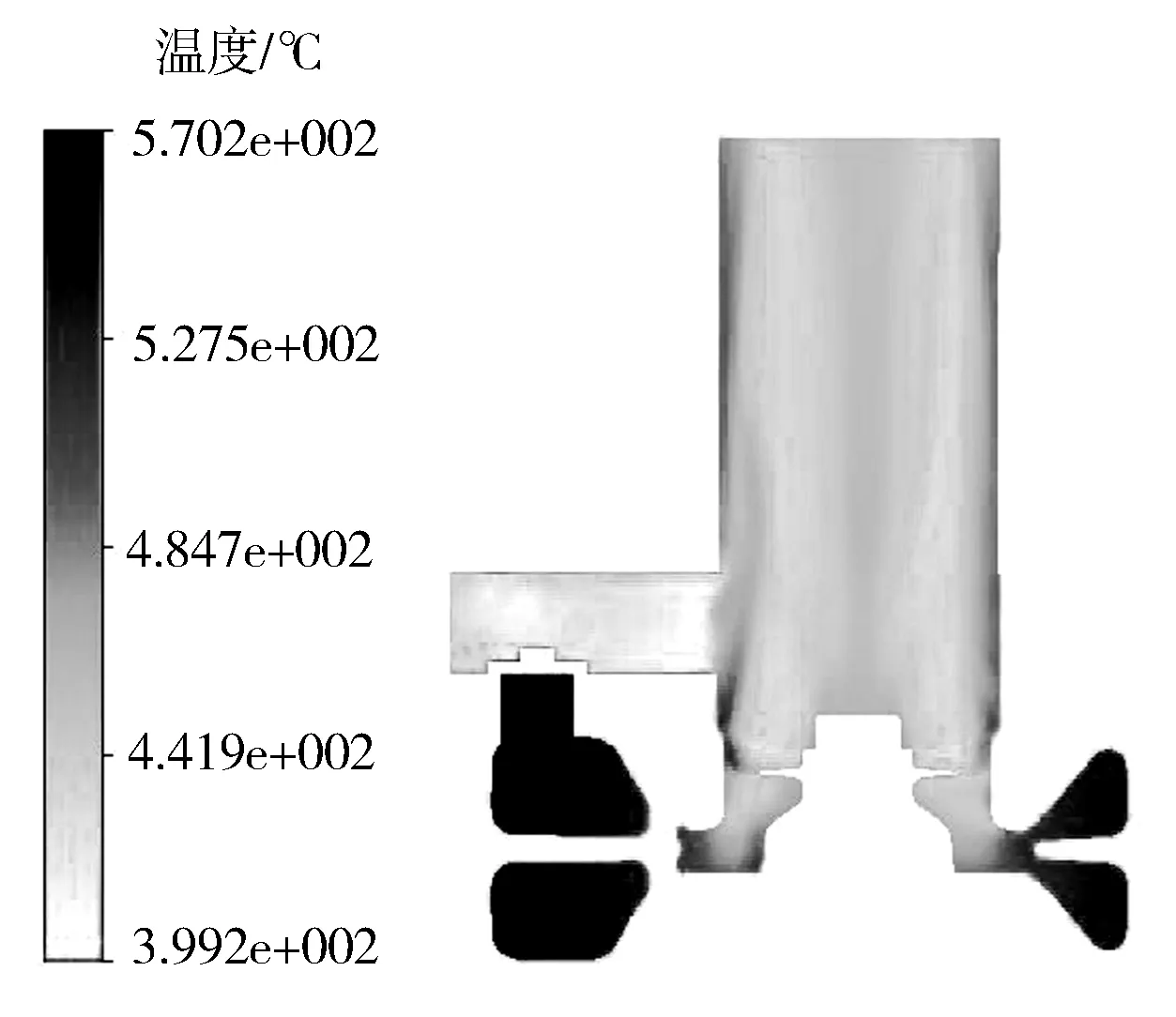
图7 100 000 r/min工况旁通阀未开启时流场xz截面温度
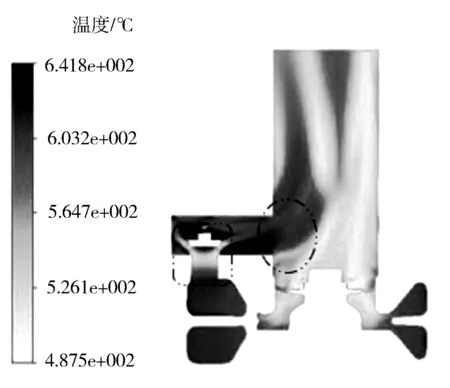
图8 110 000 r/min工况旁通阀开启时流场xz截面温度
3.2 对流场压力分布的影响
图9和图10示出50 000 r/min工况下,各模型对应的涡轮端流场xy截面和叶轮表面压力分布。
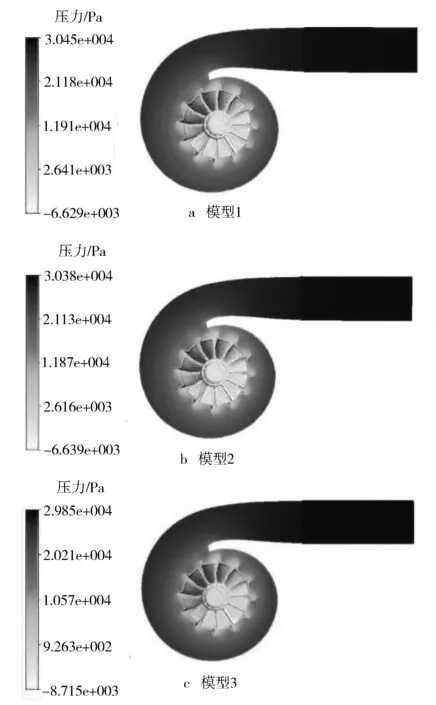
图9 50 000 r/min工况流场xy截面压力与叶轮表面压力


图10 50 000 r/min工况叶轮表面压力
气体压力沿着流动方向递减,在经过叶轮流道后,废气膨胀做功,压力下降明显。同一计算工况下,3种不同的边界条件流场压力范围分别是-6 629~30 450 Pa, -6 639~30 380 Pa和-8 715~29 850 Pa,差别很小。
3.3 对流场速度分布的影响
图11示出50 000 r/min工况下,各模型分别对应的流场速度矢量分布。由图11可以看出,不同热边界条件下流场速度矢量分布差异非常小。


图11 50 000 r/min工况流场速度分布
3.4 对涡轮效率计算的影响
涡轮增压器作为发动机的零部件,最终要参与到发动机的匹配与计算中,涡轮效率和压气机效率在匹配计算中尤为重要。图12示出在不同工况下,3个模型的计算出口温度和试验台架上的实测涡轮端出口温度。由图12可以看出,模型1完全忽略气体与流道之间的对流传热,导致各工况下的气体出口温度均高于模型2、模型3的计算出口温度和试验台架的实测出口温度,在低转速工况下,涡轮出口温度的偏差甚至达到了23 ℃。模型3计算得到的出口温度对试验数据跟随性较好,与实测数据的最大差值为3.1 ℃,出现在110 000 r/min工况下,分析可能是忽视了涡轮端蜗壳表面与环境之间的辐射换热。
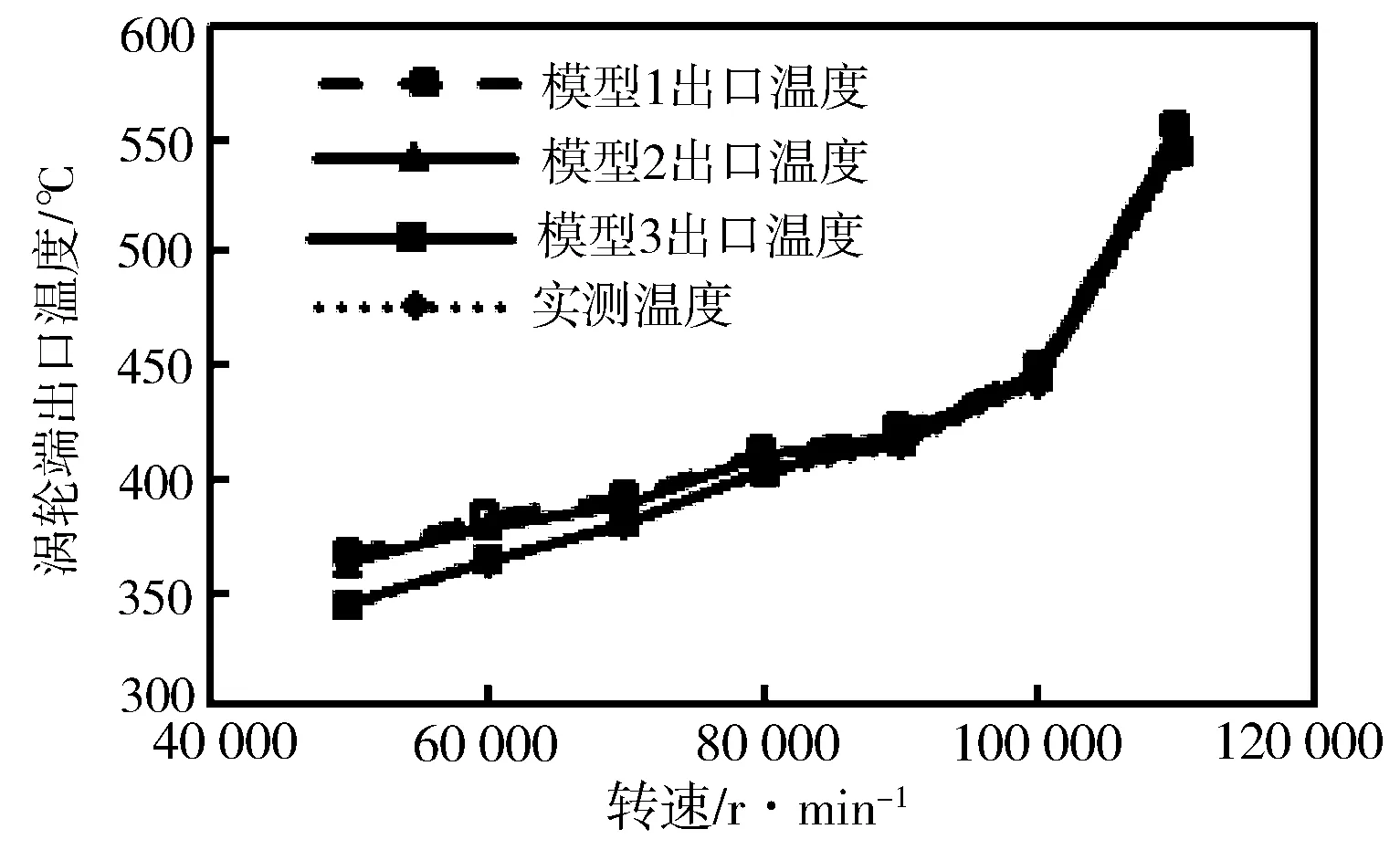
图12 涡轮端出口温度模型计算值和台架实测值的对比
图13示出基于3种模型计算得到的涡轮效率以及试验台架测得的涡轮效率。由图13可知,模型3计算值和试验值较为吻合,模型1、模型2计算值与试验值相比偏差较大且整体偏低,50 000 r/min工况下模型1计算效率和试验效率相差30%。

图13 效率模型计算值和台架试验值的对比
4 试验验证
为了对比不同热边界条件模型温度计算结果和实际温度值的差异,进行涡轮增压器热吹试验,通过温度数据采集系统采集各测点温度。试验台架由气体管道、电动阀门、燃油供给系统、润滑油供给系统、燃烧室、传感器(压力、流量、温度)和涡轮增压器等组成,试验台架原理见图14。测点的布置见表3和图15。同时进行瞬态试验研究测点温度值的瞬态特性,并探究进气条件(废气进口温度、废气进口流量)对涡轮端温度的影响。

1—双扭线流量计;2—流量计压差传感器;3—压气机入口温度/压力传感器;4—转速传感器;5—压气机;6—压气机出口温度/压力传感器;7—自循环阀;8—电动排气控制阀;9—电动微调阀;10—涡轮机;11—燃烧器;12—涡轮进气流量计;13—涡轮进气控制阀;14—气源放气阀;15—过滤器;16—气源。图14 涡轮增压器试验台架原理
表3温度测点布置
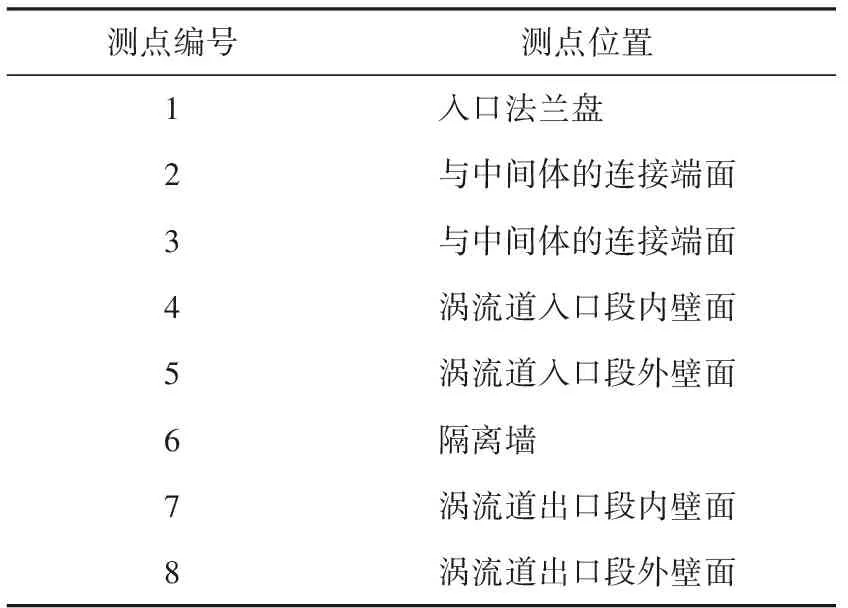
测点编号测点位置1入口法兰盘 2与中间体的连接端面3与中间体的连接端面4涡流道入口段内壁面5涡流道入口段外壁面6隔离墙 7涡流道出口段内壁面8涡流道出口段外壁面

图15 涡轮端试验测点布置
4.1 稳态试验
在50 000 r/min和110 000 r/min工况进行试验,每个工况稳定运行5 min,对传感器数据进行异常值剔除后取平均。由试验值可知,模型3的最大误差仅为4.02%,在误差允许范围内。最大误差点为中间体的连接端面,可能原因是中间体端面除了存在周围空气的自然对流传热外,还存在中间体的热传导。具体试验数据见表4和表5。
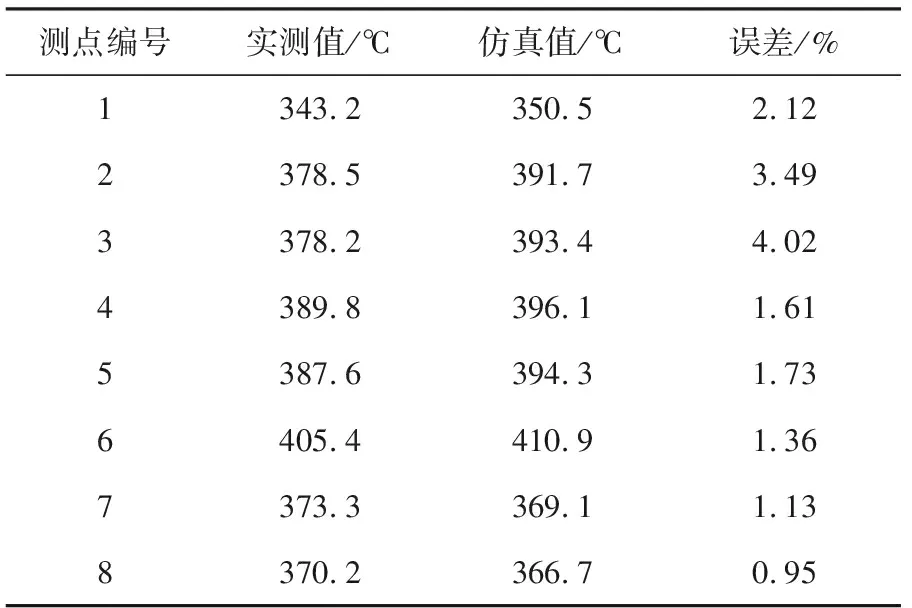
表4 50 000 r/min工况温度测点仿真值与试验值
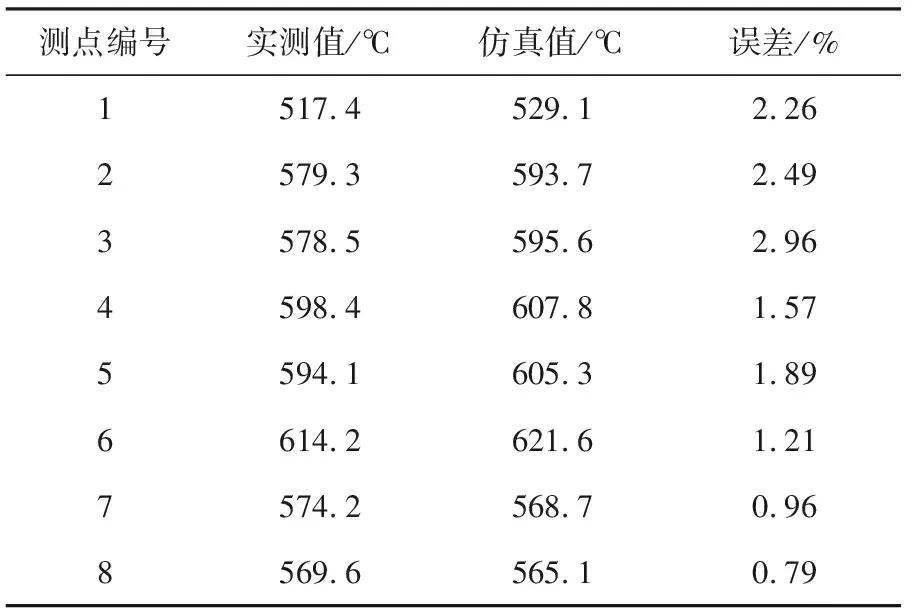
表5 110 000 r/min工况温度测点仿真值与试验值
4.2 瞬态试验
增压器在50 000 r/min工况下进入稳定状态(各测点的温度不再变化)后,调节涡轮进气控制阀使涡轮增压器转速上升至标定转速110 000 r/min,并实时记录相关试验数据。图16示出各测点温度随时间的变化情况,由图16可以看到,最终温度 和稳态试验一样,但是各测点从初始温度到达最终温度的时间不同,反映出涡轮端瞬态受热时不同部位的瞬态特性差异较大。

图16 各测点温度的瞬态变化
4.3 进气条件对涡轮端温度的影响
50 000 r/min工况下,改变废气进口温度和流量,记录各测点的温度变化情况。图17示出进气流量为0.047 kg/s,废气温度分别为427 ℃,477 ℃和527 ℃时的增压器热吹试验结果。由图17可以看出,测点温度和废气进口温度呈现正相关关系。

图17 废气进口温度对测点温度的影响
控制废气进口温度为427 ℃,调节增压器进气流量为0.094 kg/s,0.104 kg/s和0.114 kg/s,进行增压器热吹试验,记录测点温度的变化。试验结果见图18。由图18可以看到,增压器涡轮端温度受废气流量影响较小。
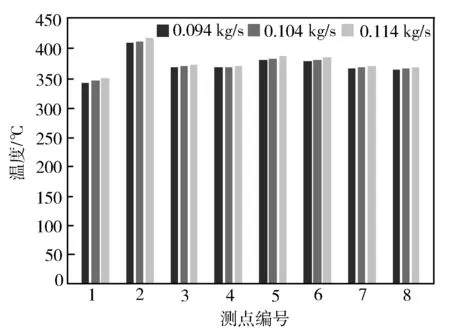
图18 废气流量对测点温度的影响
5 结论
a) 部分共轭和完全共轭传热温度场的温度分布趋势相同但是数值差异较大,50 000 r/min时差值达到25.4 ℃,完全共轭传热对涡轮增压器涡轮端试验温度的跟随较好;
b) 完全共轭传热和部分共轭传热对于流场的速度场和压力场影响不是很大;
c) 完全共轭传热和部分共轭传热对涡轮效率的影响较大,完全绝热在50 000 r/min的效率和试验值相差30%,为了进行准确的增压器匹配需要采用完全共轭传热条件;
d) 试验结果表明,增加进气温度,涡轮端的温度升高,而进气流量增加对涡轮端的温度影响不大。
