基于两段圆弧的倒推式平行泊车路径规划方法
2019-12-27张永林
张 持 张永林
(江苏科技大学电子信息学院 镇江 212003)
1 引言
随着世界各国汽车技术的飞速发展,汽车的家庭使用量急剧增加。车辆的增多,导致最直接的结果就是停车位越来越紧张,想要泊车稳准快难度比较大,对驾驶员也是一种考验[1]。泊车所引发的事故占交通事故的比例越来越大,调查显示我国保险公司接到交通事故理赔的申请中,有不少于35%是由泊车失误造成的[2]。那么,在汽车业强调电动化、自动化以及互联化的潮流下,为了缓解城市街道的压力,自动泊车系统(Automatic Parking Sys⁃tem,APS)的研究势在必行,这给出了研究自动泊车的第一个研究动机。
自动泊车系统主要有传感探测机构、决策生成机构和命令执行机构[3]。其中决策生成机构作为泊车控制器的组成核心,其生成的自动泊车路径对泊车成功具有重要意义。路径规划就是解决了车辆泊车过程中按照怎样路径引导这个问题[4]。路径规划方法主要有以下两种:第一种是基于驾驶员经验而研发出的模糊控制动态规划方法。如文献[5~6]提出了根据驾驶员的主观驾驶经验提取出控制规则,该规则能有效减小泊车过程中的控制误差。但是该规则对泊车区域规划不明确,且约束条件不易考虑周全,很难量化,因而不具有实用性。另一种方式就是通过对路径进行几何图形的规划,生成固定参考路径的静态规划方法。这种几何路径的规划方式能够根据车辆与车位之间的相对位置准确规划出无碰撞且充分考虑约束条件的泊车最佳路径,易于精确控制。REEDS等[7]采用了圆弧与直线相结合的泊车路径,但其方法路径曲率不连续,在曲率转折处需停车进行转向,这会造成很大的路径跟踪误差。PAROMTCHIK等[8]提出了回归算法,该算法采用正弦曲线将起始点和泊车终止点连接起来,若起止点变化了,正弦曲线也要随之改变,就需要重新计算一次,计算过程繁琐。文献[9~10]采用B样条曲线进行路径规划。文献[11~12]利用了五次多项式进行泊车路径规划,但是对泊车约束条件没有给出明确的规定,泊车时需要较大泊车空间,实际中很难实现。文献[13~14]对两段曲率连续的圆弧平行车位路径规划展开了研究,将泊车路径看成是两段相切的圆弧组成的序列,但是对组成两段相切圆弧的转弯半径没有给出建设性的方法。这给出了本文第二个研究动机。
本文创新性的提出了倒推式的计算策略,对两段圆弧的转弯半径进行研究。该策略的工作原理为:首先根据对泊车环境的推断,确定第二段圆弧的转弯半径为最小转弯半径Rmin。然后人为提出最大转弯半径Rmax的概念,对第一段圆弧的转弯半径在最大值与最小值之间利用二分法进行寻值。从而求出两个相切圆弧曲线的转弯半径,并在碰撞约束条件下确定泊车路径。该方法简化了路径规划过程的计算,能实现泊车路径曲率连续的要求,并针对不同的泊车起始点均能有效的完成泊车并满足泊车约束条件。
2 泊车运动学模型
在模型分析之前,先对文中所用符号进行说明,如表1所示。
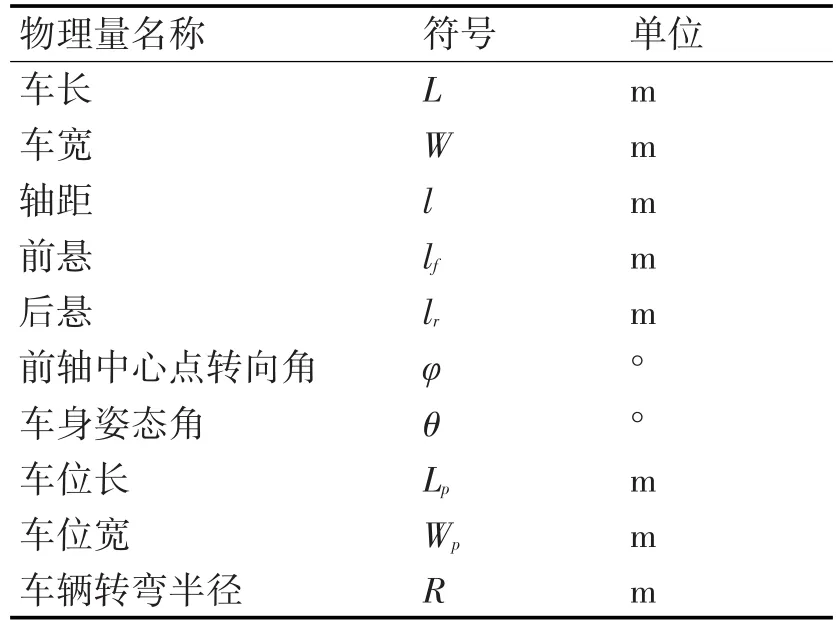
表1 符号说明
如图1所示,在大地坐标系下进行车辆模型分析。其中车辆后轴中心点坐标记为(x,y),车辆四个顶点A、B、C、D的坐标记为(xA,yA)、(xB,yB)、(xC,yC)、(xD,yD)。
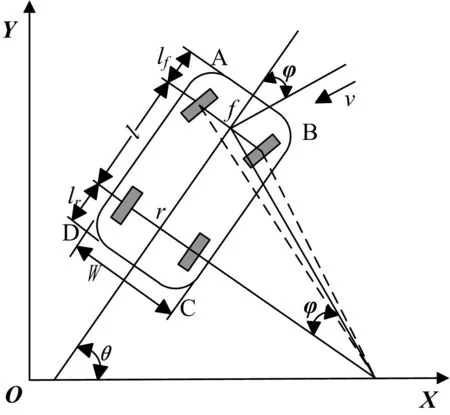
图1 车辆运动学大地坐标系
由于车辆在泊车过程中速度较低,所以车辆后轴侧滑可忽略,此时的运动系统是一个非完整约束系统,约束方程可表示为[15]

通过对式(1)推导得出下式的运动学方程:
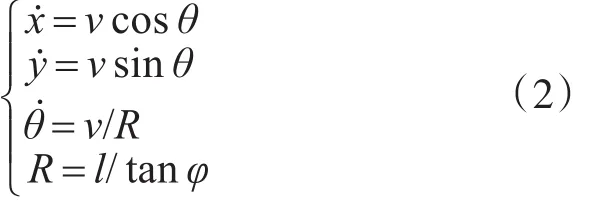
此外,将车身前方两个顶点的运动轨迹方程表示为
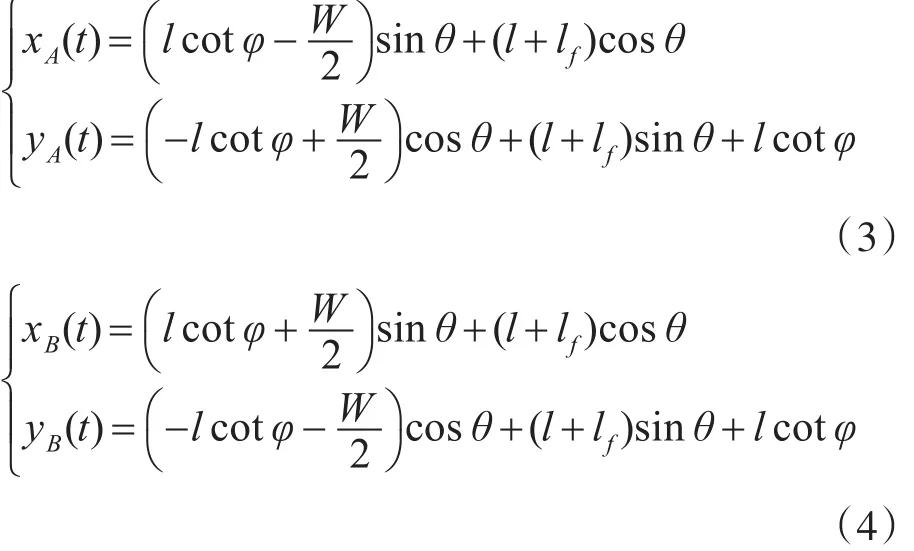
3 平行泊车路径规划
3.1 倒推式平行泊车路径规划
如图2所示,以车位左下角为坐标原点,以车辆后轴中心点作为参考点,建立泊车运动路径直角坐标系。车辆从P0行驶到泊车起始点P1的过程中,车身周围的传感器模块探测右侧的车位情况,并计算出车位大小深度。结合泊车起始点P1点所在位置,控制器根据车位情况计算确定泊车的终止点P2的位置,从而根据车位环境确定了起始点和终止点,开始泊车路径的规划。

图2 两段圆弧曲线泊车轨迹示意图
图2中,将两段曲率连续的相切圆弧作为泊车路径,泊车路径从泊车起始点P1过渡到终止点P2,且过程中保证车辆不会碰到车位边界,两段弧半径大于等于车辆最小转弯半径。泊车起始点P1记为(x,y),从泊车起始点起,第一段圆弧记为圆弧1,其圆心坐标为O1(x1,y1),第二段圆弧记为圆弧2,其圆心坐标为O2(x2,y2),泊车路径终止点P1(x3,y3),停车区域左前方拐点为P(Px,Py),E为两段圆弧的相切点即两圆心连线与泊车路径的交点,记泊车区域上边界的纵坐标为y=yup。
在进行路径规划前,首先需对泊车路径的约束条件进行论述:
1)圆弧2的圆心O2到车辆右前头的距离需小于O2到拐点P的距离:
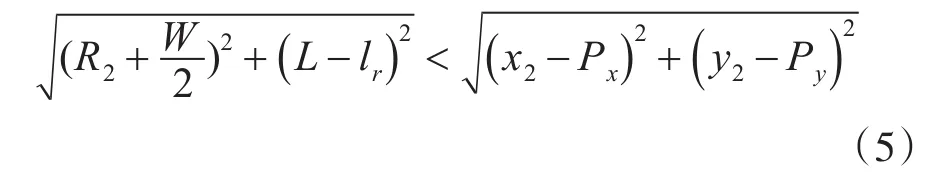
2)拐点P到圆弧1圆心O1的距离需小于圆弧1圆心O1到车辆右后方的距离:
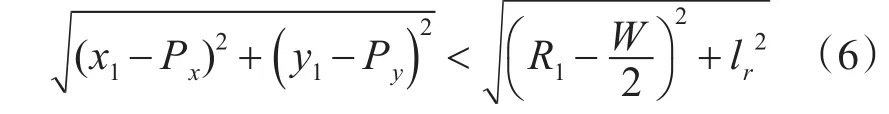
3)圆心O1到车辆左前方的距离需小于圆心O1到上边界的距离。

4)车辆自身也存在约束条件,由于车辆存在最小转弯半径Rmin,当车辆处于最小转弯半径时,曲率最大。所以后轴中心点轨迹曲线的曲率K需满足K≤1 Rmin。同时前轮转向角速度应有 φ̇≤φ̇max。
基于倒推的方式就是首先确定第二段圆弧的半径为最小转弯半径,再根据其推论出第一段圆弧的半径大小。根据以上约束条件,对泊车路径中两段圆弧的半径分别进行分析判断。
1)圆弧2的圆心及半径大小确定
在起始点和终止点位置确定且设定合理的前提情况下,有以下推断。
在终点位置确定的条件下,第二段圆弧的半径越小,车辆右前方车头距离停车位的拐点P则越远,发生碰撞的可能性越小;在起始点位置确定的条件下,第一段圆弧半径越大,车辆左前方车头与泊车区域上边界碰撞的可能性越低,且与P点的距离越远。因此,取车辆最小转弯半径作为圆弧2的半径。从而可确定圆弧2的圆心坐标O2(x3,y3+Rmin)。
2)圆弧1的圆心及半径大小的确定
车辆只有最小转弯半径而不存在最大转弯半径。为了便于数值的计算,在平行泊车的前提下人为设定最大转弯半径以达到确定圆弧1半径的目的。
根据初始点和终止点的相关信息来求解最大转弯半径:
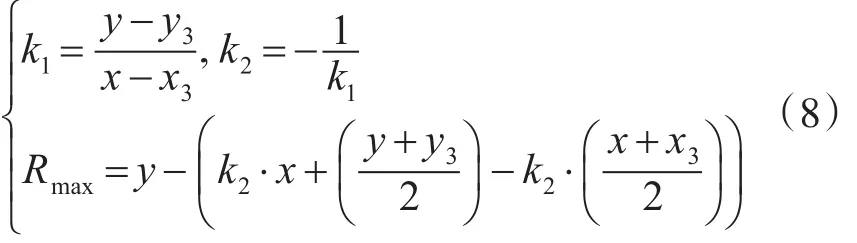
所以,通过求解最大转弯半径,此处圆弧1半径存在最大和最小转弯半径。
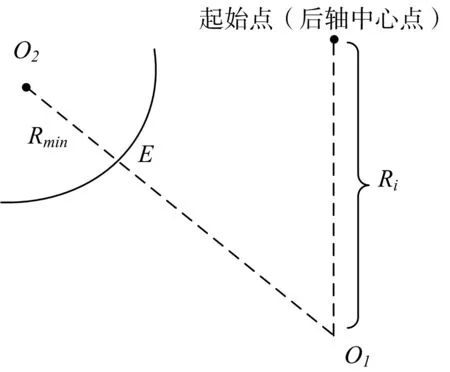
图3 圆弧1半径求解分析图
如图3所示,E为圆弧1圆心和圆弧2圆心连线与泊车路径的交点。理论上,若圆弧1与圆弧2相切,有O1E=R1,所以令此处的R1值即为所求的半径。此处,对圆弧1的半径R1,有 Rmin≤R1≤Rmax,因此,只需找到介于最大和最小半径之间的合理R值即可。
令li为介于最大和最小半径之间的值,有Rmin≤li≤Rmax,如果当li=R1时,此li值即为所求的圆弧1半径,取l1和l2,令其取值范围为 l1≤Rmax,l2≥Rmin。
3.2 二分法查找介于两者之间的最终解
当圆弧1的半径为最小转弯半径时,圆弧1的圆心坐标为Omin(x,y-Rmin)。假设此时使圆弧Omin与圆弧2相切的半径为l2,如式(9),比较l2与Rmin的大小。

并求解直线O2Omin与X轴所成的夹角ωmin,如式(10),此处的夹角为锐角。
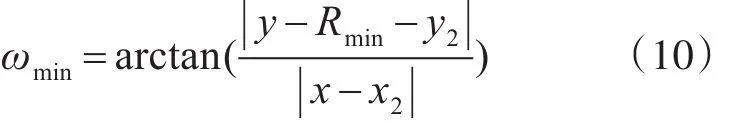
同理,当圆弧1的半径为最大转弯半径时,可求得相关的l1和ωmax。
若 l2>Rmin,l1<Rmax,则计算 ωmax和 ωmin的中间值,有:
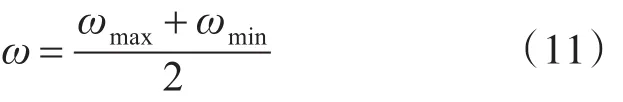
求解过圆弧2圆心且斜率为-tanω的直线与以(x,y)为起始点且沿y轴负方向的射线的交点到圆心O2构成线段的长度。假设交点为Om,则lm=O2Om-Rmin,有:

比较lm与OmP1的大小。若lm>OmP1,则以线段OmP1的长度替代最小转弯半径;若lm<OmP1,则以线段OmP1的长度替代最大转弯半径。
迭代上述过程直到lm=OmP1,此时,所求解得的半径R1使得圆弧1与圆弧2相切。
3.3 碰撞判断
为实现泊车路径的避障,需进行碰撞判断。在起始点和终止点时,车辆均平行于X轴,一般存在如图4所示碰撞点①和②的碰撞情况。

图4 碰撞点示意图
1)碰撞判断1
在进行圆弧1的泊车时,车辆左前方可能会与上边界①发生碰撞。如图5所示,圆心点O1到车辆左前方A的距离为d1,圆心O1到上边界的垂直距离为 yup-y1,比较两者大小。距离d1可表示为

上图中,θ为两段圆弧所对的圆心角,α0为线段O1A与圆心O1到上边界的垂直线段之间形成的夹角。以此两角作为判断条件:
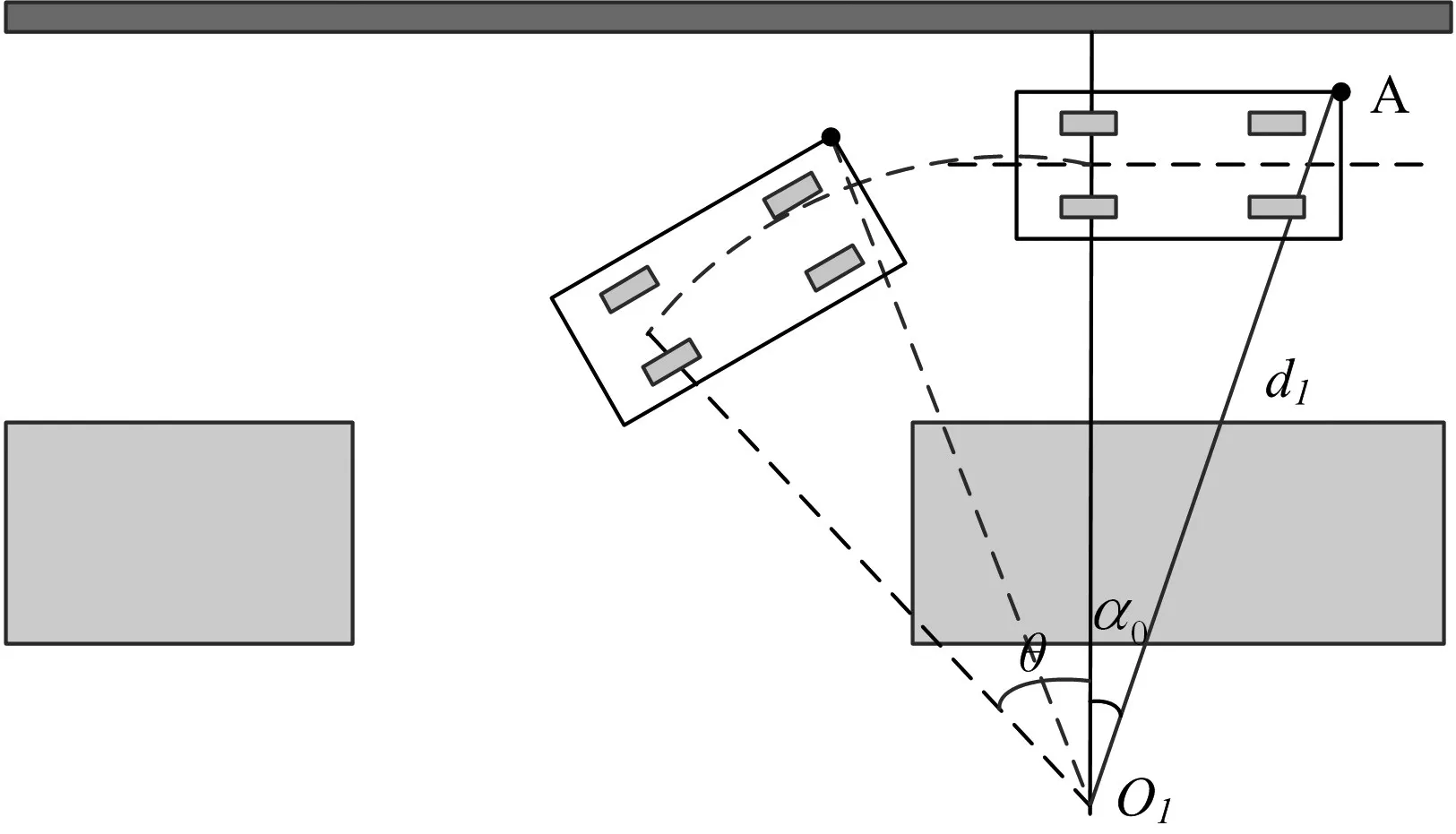
图5 上边界碰撞判断
(1)若θ>α0,说明车辆在泊车过程中d1所在线段会存在与X轴垂直的情况。比较 yup-y1和d1值的大小。
(2)若θ<α0,说明车辆在泊车过程中d1所在线段不会存在与X轴垂直的情况,即与X轴正方向夹角为锐角。比较 yup-y1和 d1⋅cos(α0-θ)值大小。
2)碰撞判断2
如图6所示,当车辆泊车到圆弧2时,车辆右前方B可能会与拐点P碰撞。给出如下判断条件:

图6 车位左前方碰撞判断
将此时判断条件由点到点的距离比较转换为投影到X轴上水平线段大小的比较,即将O2P与O2B的比较转换为线段O2P投影在X轴上的水平距离与当车辆右顶点行驶到线段O2P所在的直线上时线段O2B投影在X轴上的水平距离的比较。
其中,线段O2B的长度d2可以表示为
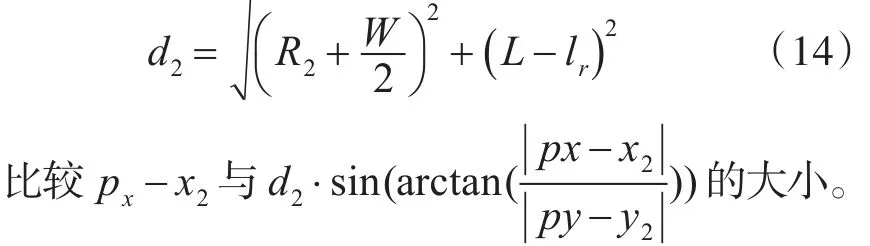
4 平行泊车路径规划数值分析
本节通过多个案例验证所提出的倒推式两段圆弧自动泊车路径规划方案在各种泊车工况下的可行性。
4.1 倒推式泊车路径规划的仿真
一般的家用轿车中型车的长度在4.3m~4.7m,宽度在1.7m~1.8m;中大型轿车长度在4.6m~4.9m,宽度在1.7m~1.9m之间。通常情况,平行车位的长度应是车身长度的1.4倍~1.6倍,车位的长度一般在6m~7m,车位宽度一般在2m~2.4m之间[16]。
根据上述平行车位尺寸的标准与要求,为了模拟真实车位环境,将选取的车位尺寸和车辆长宽尺寸列如表2。
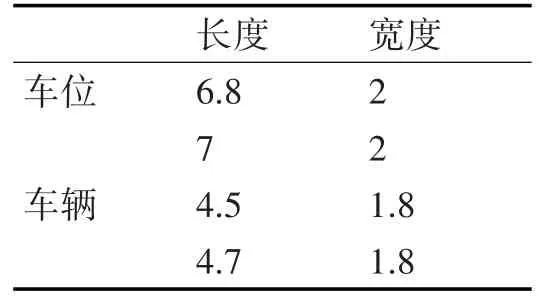
表2 车位和车辆尺寸
仿真结果如下,图7为在车位6.8m×2m,上边界纵坐标为6.5m的车身环境中,车辆大小为4.7m×1.8m的不同泊车起始点泊车轨迹。
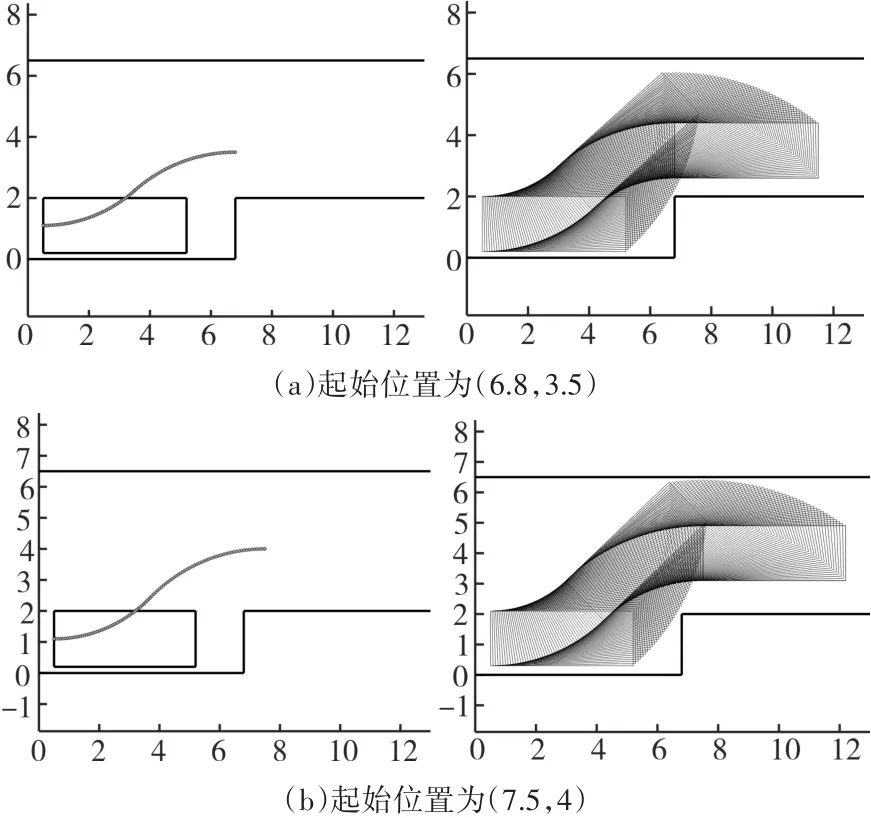
图7 后轴中心点泊车轨迹和车辆运行轨迹
图8为在车位6.8m×2m,上边界纵坐标为7m的车身环境中,车辆大小为4.5m×1.8m的不同泊车起始点泊车轨迹。
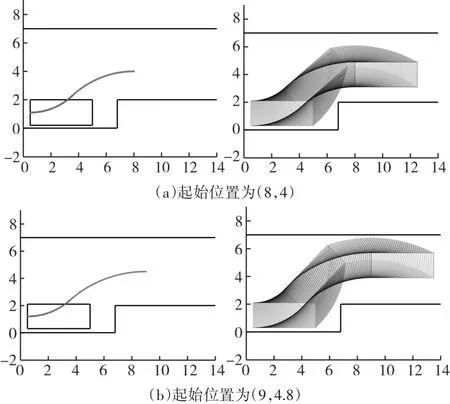
图8 后轴中心点泊车轨迹和车辆运行轨迹
图9为在车位7m×2m,上边界纵坐标为7.5m的车身环境中,车辆大小为4.5m×1.8m的不同起始点泊车运行轨迹。
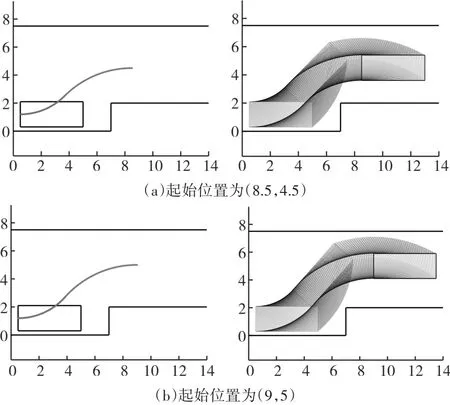
图9 后轴中心点泊车轨迹和车辆运行轨迹
通过比较图7和图8,可总结出在车位相同的情况下,不同大小的车都能够实现泊车入位。比较图8和图9,当车位变大时,车辆停入车位的后方距离会随之增大,但对泊车效果没有影响。
实验仿真证明,此路径规划方法可实现不同车位、不同大小车辆和不同起始点位置的泊车运动,能应对实际泊车中遇到的各种车位情况,为自动泊车提供可靠可行的泊车路径。
4.2 路径规划的拟合仿真结果
在倒车过程中,车辆运行轨迹呈现阶跃式变化。当车辆行驶到两段圆弧相切点时,转向角值会有一个较大的跳变,所行驶的路径也会有波动,对泊车效果会有影响。所以需对两段圆弧路径进行拟合,拟合出一条连续曲线。
利用反正切函数对泊车路径进行拟合,拟合的结果如图10所示,拟合曲线能够有效地贴近两段圆弧泊车路径。
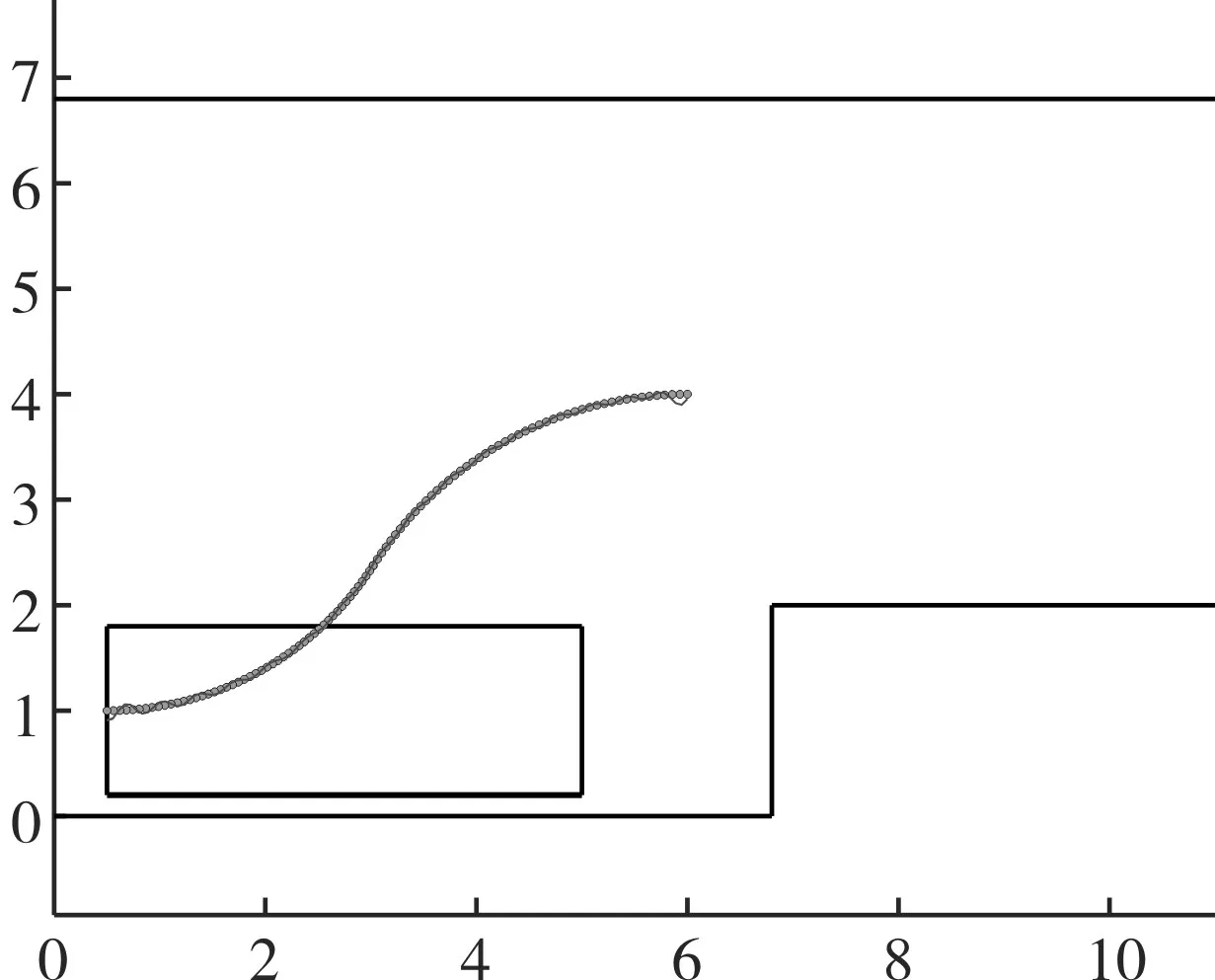
图10 泊车路径拟合
反正切函数形式如下:
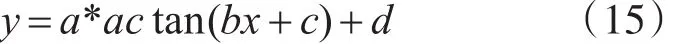
式中的a、b、c、d为可改变曲线形状的参数,修改这些参数可使曲线接近所要的两段圆弧泊车轨迹。将坐标点(8.5,3.8)作为起始点,适当的选取转弯半径的R1以及R2的大小,拟合得反正切函数为
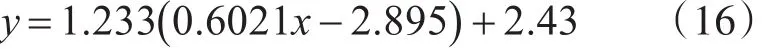
5 结语
本文研究了自动泊车路径规划问题。首先在大地坐标系下结合车辆在低速行驶状态下的特性,建立了车辆运动学模型。然后依据所建运动模型提出了一种基于两段圆弧的倒推式平行泊车路径规划方案,该方案采用二分法寻找最佳半径并给出了车辆碰撞判断条件。最后通过多个案例验证了所提方案可实现不同泊车起始点的路径规划,并对两段圆弧泊车路径使用反正切函数进行拟合,得出一段曲率连续的泊车路径,有效加强了泊车的连贯性。
