阶梯溢流坝与二级消力池联合消能体型研究

张荣斌，李 阳

(1. 云南省水利水电勘测设计研究院，云南 昆明 650021；2. 武汉大学水利水电学院，湖北 武汉 430072)

阶梯式溢流坝是一种具有较高消能率的消能泄水建筑物，在国内外工程中已得到大量的应用。它主要利用阶梯上水流形成的横向漩滚及其与主流之间的剪切和动量交换来达到消能目的。从20世纪80年代起，国内外对阶梯式消能工水力特性展开了广泛的研究。Sorensen对新蒙克斯维里坝进行的模型试验研究表明：当坝面水流流速较低，水深较浅时阶梯上会出现水流偏折现象，这种现象可通过设置尺寸由小到大的过渡阶段来消除[1]。Stephenson针对阶梯尺寸，溢流坝面坡度等对阶梯式溢流坝的影响进行的模型试验表明：采用阶梯消能时下游溢洪道坡度为1∶10～1∶5时消能效果最好，可用增大阶梯尺寸来增加消能效果[2]。王均星利用紊流数值模拟的方法，对阶梯尺寸进行对比分析研究，提出合理的阶梯形式和布置长度可以明显改善水流流态，优化沿程压力分布，提高阶梯消能率[3]。陈群发现单宽流量越大，则消能率越低，并对影响阶梯溢流坝的因素进行了分析[4]。曾丹结合凯乐塔水电站工程的水力学模型试验，选用3D紊流模型，对其阶梯式溢流坝流场进行了三维数值模拟[5]。目前对于阶梯溢流坝的研究大多数仅限于单级阶梯溢流坝的体型、消能研究，对于阶梯溢流坝与二级消力池联合消能的水力特性研究并不充分。

1 工程概况

1.1 工程概况

本文将依托绿冲河退水道的阶梯溢流坝，采用模型试验与数值模拟结合的方法，主要探究二级消力池及溢流坝上游局部尺寸对于水力特性的影响。绿冲河退水道位于大坡子隧洞出口，右侧为绿冲河倒虹吸进口，左侧为绿冲河退水道，全长345.683 m。绿冲河退水道由退水闸段、转弯段、一级消力池段、二级消力池段等组成。退水闸长6 m，堰型为有闸控制宽顶堰，设计退水流量20 m3/s，上游水位为1 418.045 m，堰宽为3.8 m，工作水头1 418.045 m，堰顶高程1 415.045 m。消能方式为台阶+底流消能，转弯段长25.527 m，宽3.8 m，一级消力池长18.68 m，宽3.8 m，底板高程1 298.352 m，共82阶台阶；二级消力池长30 m，宽3.8 m，底板高程1 270.000 m，经过消能后的水流放入下游冲沟。以坝轴线为桩号0+000.000点，纵剖面示意图见图1所示。

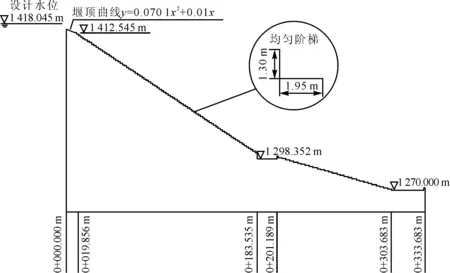
图1 原设计阶梯式溢流坝剖面图(单位：m)

1.2 初拟方案

初步设计拟定了以入流台阶尺寸、消力池入池、出池断面尺寸为变量的两种体型方案，方案二与方案一的差别体现在以下几处：

1)取消入流挑坎后的三个均匀台阶，在桩号0+019.856处开始设置高度由小变大的6个台阶；

2)一级消力池入池端取消上游3个台阶，替换为坡度1∶1.125的斜坡；出池端加高消力池尾坎高度0.9 m，并考虑出池水流与下游台阶水流的衔接，接1∶1.84的斜坡，斜坡底高程为1 299.325 m；

3)二级消力池入池端上游2个台阶进行调整，设置底坡为1∶2.333的斜坡段。

具体尺寸对比见表1。以上述两方案为基础，通过数值模拟研究各参数变化时其水力特性变化规律以及对泄洪消能效果的影响。

表1 溢流坝不同体型组合方案表

2 阶梯溢流坝数值计算

2.1 模型建立及网格划分

紊流作为一种高度非线性的复杂流动，数值模拟一般是通过一定的数值方法和模型对其进行分析。在Fluent中提供了以下几种湍流模型：普朗特混合长度模型，一方程湍流能量方程，二方程k-ε模型，重整化群模型(RNGk-ε)和大涡模型。本文采用RNGk-ε模型。通过在大尺度运动和修正后的粘度项体现小尺度的影响，将小尺度运动从控制方程中排除。模型计算区域分为三个区块，上游到下游依次为水库、一级溢流坝、中段消力池以及二级溢流坝。在划分网格时考虑到来流流量较小的特点，水流充满水库与溢流时间较长，为平稳水流，增加计算速度，且考虑到各区块流态复杂程度，单元尺寸在进口段(区域1)、一级溢流坝段(区域2)和二级溢流坝段(区域3)均采用0.2 m×0.2 m×0.2 m，有效网格数约386万。

本次计算区域边界条件：采用压力进口和压力出口边界(Pressure)，通过设定该处控制水位实现；各网格计算区域底部采用无滑移壁面边界(Wall)；消力池及溢流坝两侧设置对称边界(Symmetry)条件；计算区域上方设置压力边界，P=0。

几何模型及网格划分布置如图2所示。

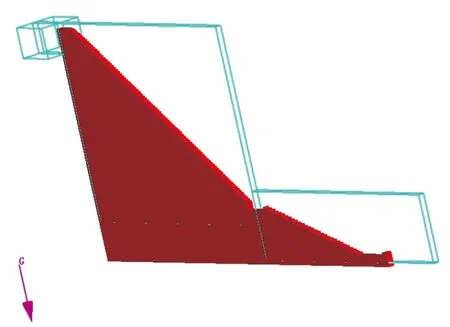
图2 几何模型及网格划分示意图

2.2 数值方法可靠性分析

为了保证所选用的数值模型计算准确，将数模计算结果与物模试验结果进行初步对照，取方案一典型断面测点水深、流速进行数据对比，如图3所示。

由图3所示，溢流坝各典型测点计算数据与模型试验数据误差在10%以内，考虑实验误差可认为本数值模拟结果较为可靠。

2.3 数值模拟结果分析

2.3.1 流态

方案一中，上游量水堰来流平稳，水流较为平顺过流并逐步加速滑移至阶梯溢流坝前端，挑坎上的水流收缩水深为0.6 m，经过挑坎后水流壅高且掺气膨胀隆起，在经过六级台阶，从桩号为0+026.395 m处开始逐渐平顺下泄，掺气较为均匀，但偶有波动，泄流流入一级消力池后发生剧烈漩滚，且在入流下部形成稳定空腔，消力池出流波动较为明显，且有少量飞溅，下游溢流坝面流态较差，二级消力池中流态较差，漩滚明显，消能不充分。相比方案一，方案二中调整入流台阶体型后入流更为平顺，掺气均匀，泄流经斜坡流入一级消力池后池内流态有明显改善，空腔减少，在加高尾坎后池内消能更为充分，下游溢流坝面水流流态有较大改善。各方案中两级消力池流态如图4所示。

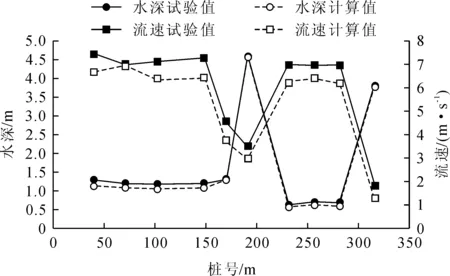
图3 数模计算结果与试验结果对照图

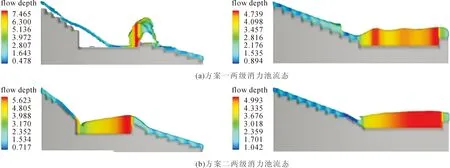
图4 各方案中两级消力池流态图

2.3.2 沿程水深及流速

方案一中，绿冲河溢洪道起始段桩号0+000.000处水深1.53 m。堰后及挑坎段水深1.13 m～0.60 m，0.60 m为挑坎上的水流收缩水深，流速9.50 m/s。泄槽中上部水流脱离台阶，桩号0+040.187 m处水深1.30 m，流速7.50 m/s。桩号0+049.939 m处水深1.20 m，流速5.55 m/s。一级消力池开始段，水流水深1.18～1.20 m，流速4.45～7.30 m/s。一级消力池末至二级消力池开始段，水流水深0.58～0.88 m，流速6.00～7.40 m/s。方案二中，绿冲河溢洪道起始段桩号0+000.000处水深为1.58 m。堰后水深1.05～0.60 m，流速4.75～8.50 m/s。桩号0+055.789 m处水深1.33 m，流速3.05 m/s。一级消力池开始段，水流水深0.50～1.35 m，流速1.70～8.15 m/s。一级消力池末至二级消力池前开始段，水流水深0.63～0.70 m，流速6.50～7.10 m/s。对比发现，方案二中沿程水深较方案一中更大，相应沿程流速较小，各方案流速水深及其对比如图5、图6所示。

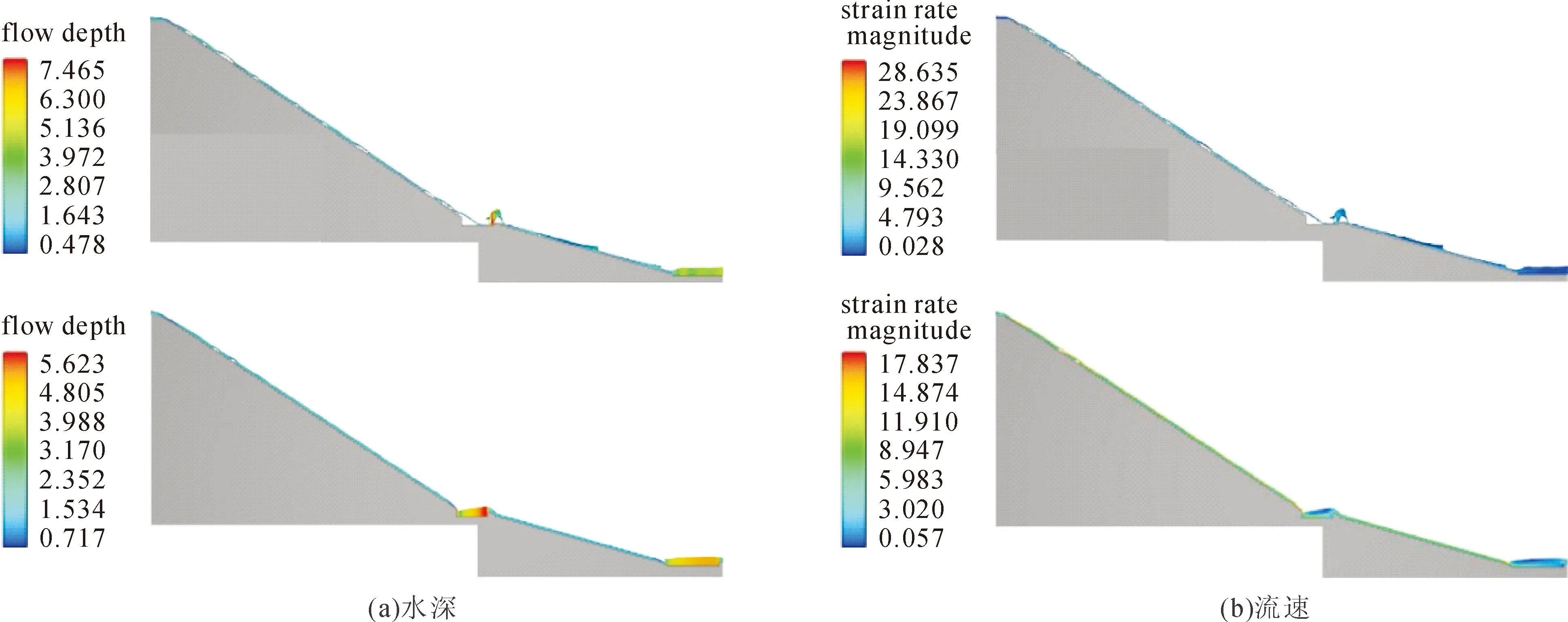
图5 各方案沿程水深及流速图

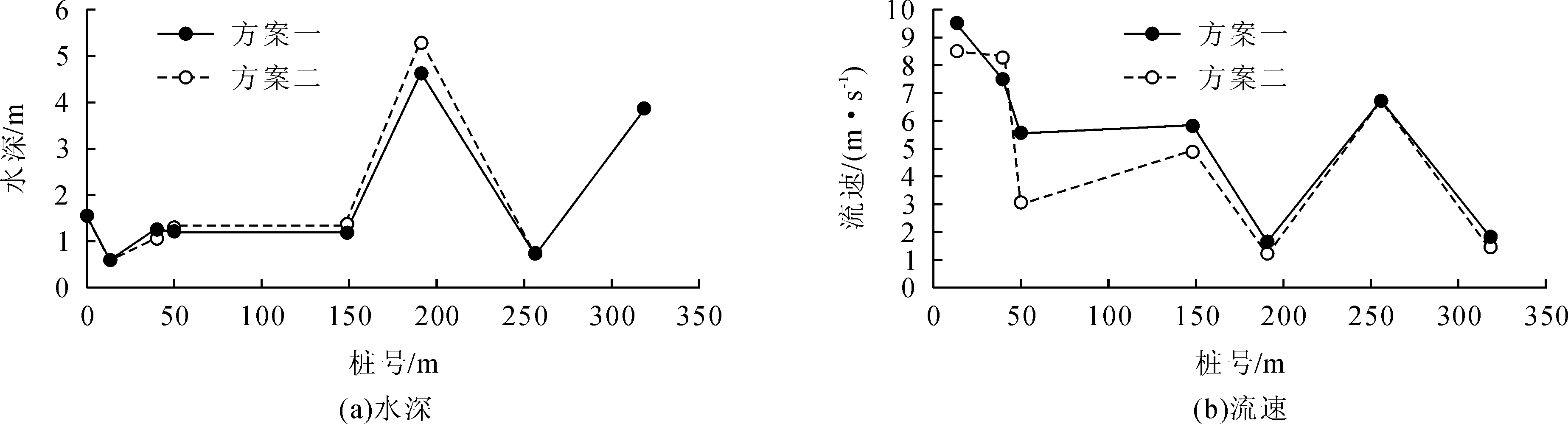
图6 各方案沿程水深及流速对比图

2.3.3 压强分析

因阶梯溢流坝面掺气较充分，因此无需考虑坝面空蚀空化问题，由于消力池底板常受水流直接冲击，其时均压强以及脉动压强成为常见的重要指标之一，设计流量工况下，消力池的底部时均、脉动压强值见表2。

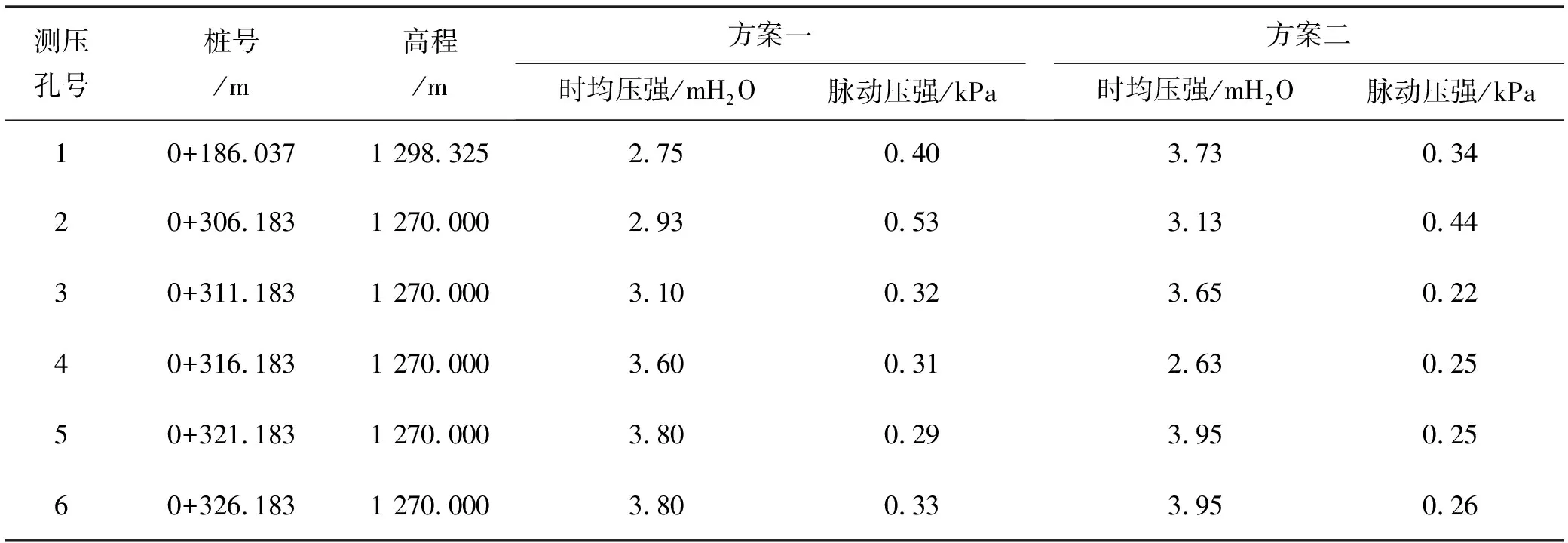
表2 消力池底板压强表

由表2可知，方案一中消力池底板时均压强均在2.75～3.80 m H2O间波动，与消力池内水深变化规律一致，而二级消力池中脉动压强最大值出现在入池断面，表明该断面水流波动最为剧烈，对池底冲击最为剧烈。结合流态分析，此断面水流从坝面跌入消力池，上下漩滚剧烈，冲击消力池底板，与压强分布规律相符，脉动压强最大值达0.53 kPa，远远小于建筑安全设计脉动压强，方案二整体时均压力较方案一更小，最大脉动压强只有0.44 kPa，表明二级消力池的尺寸体型修正能降低入池水流对于消力池底板的冲刷，工程运行更为安全。

2.3.4 消能效果分析

溢洪道消能率的计算采用应用最广泛的消能率计算公式：

式中：E1为以下游消力池底部为基准面的上游控制段断面水流总能量(取控制段桩号0+000.000 m断面为计算断面)；E2为二级消力池末端断面水流总能量。

两种方案计算结果如表3所示。

表3 方案一、二消能率计算表

比较两个方案消能率可知，整体消能率未出现较大变化，均在97%以上，表明两个方案均满足消能要求。

3 结 语

1)利用RNGk-ε紊流模型对绿冲河退水道阶梯溢流坝与两级消力池联合消能进行数值模拟，计算结果与物理模型试验数据较吻合，说明RNGk-ε紊流模型对联合消能模拟的可靠性较高。

2)采用两级溢流坝+两级消力池能有效达到消能的目的，阶梯溢流坝入流端采用小尺寸逐渐过渡到均匀尺寸台阶的组合能有效调整入流流态，消力池入池端采用斜坡代替台阶能调整入池下跌水流角度，减少对于消力池底板的冲刷，优化思路可供类似工程进行参考。