协作机器人动力学参数辨识方法研究*
2019-12-26潘炳伟蒋劲峰薛佩姣
潘炳伟,吕 燕,蒋劲峰,薛佩姣
上海电气集团股份有限公司 中央研究院 上海 200070
1 研究背景
如果要提高高速、重载、高精度机器人的控制精度,那么需要采用构建更加先进的考虑机器人动力学模型的控制方法,如力矩控制、动力学前馈控制等。由于机器人的动力学模型体现了机器人内在的力与运动关系,因此基于机器人动力学模型的控制方法可以实时、准确地给出机器人进行目标运动所需要的力矩值[1]。
随着工业、医疗及服务业水平的不断提高,人们迫切希望工业机器人能够与人类协同工作,人机协作的需求越来越强烈,协作机器人得到了快速发展。拖动示教和碰撞检测功能是实现人机协作的基础,实现这两个功能,需要精准的动力学模型。得到精准动力学模型的前提是进行动力学参数辨识。
惯性参数是机器人动力学模型分析的重要指标之一,决定机器人末端执行器的控制精度,在机器人动力学研究中占据重要地位。惯性参数需要借助参数辨识的方法进行获取,惯性参数的辨识问题一直是国内外专家学者研究的重点,为人们所关注和重视。惯性参数的辨识方法大致可以分为五类:解体测量法[2-3]、计算机辅助设计法[4-5]、不解体测量法、理论辨识法、加装传感器辨识法。
笔者对影响动力学参数辨识的因素——机器人关节摩擦进行建模与分析,设计关节摩擦力矩和重力矩的测量试验,基于实测摩擦数据,研究动态力矩对摩擦力矩,即库伦摩擦的影响,并应用关节匀速运动轨迹法对黏性摩擦系数进行拟合与对比。笔者在研究中提出基于连接组合体的机械臂惯性参数分步辨识方法,这一方法将关节锁定,无论机器人关节数目多少,每次的辨识对象都是末端连杆。应用这一方法,每次辨识相互独立,不需要将辨识结果带入其它辨识中,误差累积大大减小。这一方法对每个连杆组合体的惯性参数分别进行辨识,参数辨识精度高,尤其是对于靠近基座的关节而言。
2 协作机器人运动学理论
串联机器人由一系列连杆连接构成,通常应用Denavit-Hartenberg模型进行研究。为了清晰描述每个连杆与相邻连杆之间的相对位置关系,需要在每个连杆上定义一个坐标系。将固连于连杆上的坐标系称为连杆坐标系[6-7]。
将固连于机器人基座上的坐标系定义为坐标系{0},该坐标系通常固定不动,作为参考坐标系。在这个参考坐标系中,可以描述机器人其它连杆坐标系的位置。为了使问题简化,通常设定Z0轴为沿关节轴1方向。
3 协作机器人连杆坐标系与连杆参数
对于协作机器人而言,所有关节都是旋转关节。对机器人各机械臂建立连杆坐标系,如图1所示。根据Denavit-Hartenberg模型和图1,推算出机器人的连杆参数,见表1。
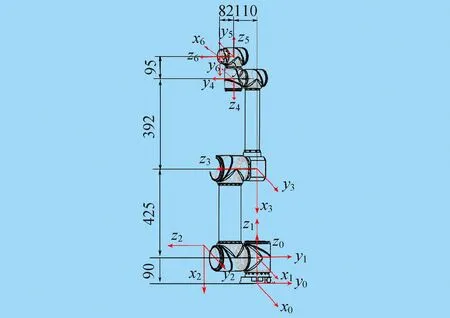
图1 协作机器人连杆坐标系
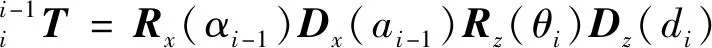
(1)
式中:Rx(αi-1)为绕x轴旋转αi-1角度的旋转变换矩阵;Dx(ai-1)为沿x轴平移ai-1距离的平移变换矩阵;Rz(θi)为绕z轴旋转θi角度的旋转变换矩阵;Dz(di)为沿z轴平移di距离的平移变换矩阵。
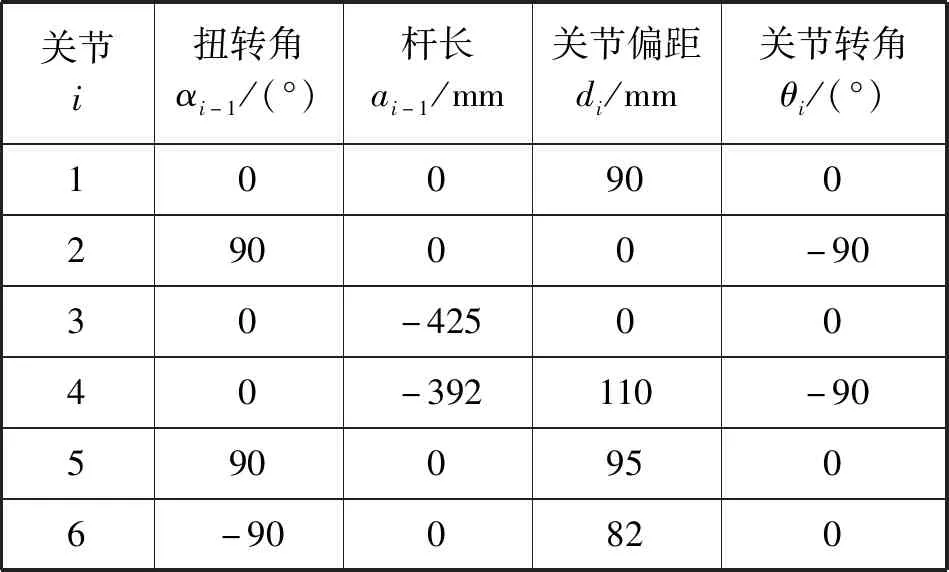
表1 协作机器人连杆参数
根据协作机器人的连杆参数,可以求出每一个连杆的变换矩阵,从而求出运动学正反解。
4 协作机器人动力学模型
根据牛顿-欧拉动力学建模,得到协作机器人动力学模型为:
τ=τf+τd
(2)
(3)
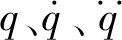
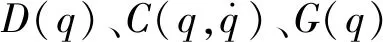
pg=[Ixx,Ixy,Ixz,Iyy,Iyz,Izz,Hx,Hy,
Hz,m]
(4)
(5)
式中:Ixx、Ixy、Ixz、Iyy、Iyz、Izz为机器人惯量矩阵I中的六个参数;rcx、rcy、rcz为质心向量;m为质量。
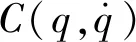
机器人的动力学参数主要包括机械臂的惯性参数及关节摩擦参数,关节摩擦参数取决于所采用的摩擦模型。尽管摩擦是一种非常复杂的非线性现象,但对于大多数机器人系统而言,其线性近似模型可以保证所需的精度。因此,协作机器人动力学参数辨识一般采用线性摩擦模型[8]:
(6)
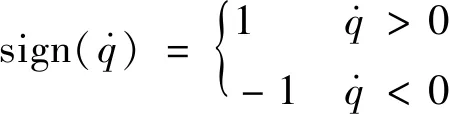
(7)
式中:σ为黏性摩擦系数,N·m·s/rad;fc为库仑摩擦常数,N·m;μ为库仑摩擦动态力矩因数。
由此,完整的动力学参数写为向量形式为:
pd=[Ixx,Ixy,Ixz,Iyy,Iyz,Izz,Hx,Hy,Hz,m,
σ,fc,μ]
(8)
pd就是协作机器人动力学参数辨识的对象,每个关节均包含十个机械臂惯性参数与三个关节摩擦参数,因此每个关节的动力学参数均可表示为式(8)的形式。
5 机器人关节摩擦特性分析及建模
对于任意机器人关节i,若关节的轴线始终与重力方向平行,即满足平行条件,则当关节i恒速运动时,其余关节锁住不动,惯性力为零,输入力矩等于摩擦力矩。为提取摩擦数据,可使关节i由θ1恒速转动至θ2,以不同的恒速重复多组试验,得到不同速度下的摩擦数据。
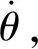
(9)
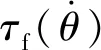
试验②运动方向与试验①相反,输入力矩u2为:
(10)
对于笔者研究的协作机器人,由于采用高精度的旋转矢量减速机和谐波减速器传动,正反摩擦力矩差异很小,因而有:
(11)
由式(9)至式(11)可以得到摩擦力矩、重力矩分别为:
(12)
τg(θ)=(u1+u2)/2
(13)
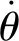
另一方面,重力矩也可以表示为:
τg(θ)=rcxmgcosθ+rcymgsinθ
(14)
式中:rcx、rcy分别为第i个连杆的质心在连杆坐标系{i}中x方向和y方向上的表示。
根据式(12)至式(14)能够将rcxmg和rcymg求解出来,然后求解出不同角度位置的重力矩。
在协作机器人中,满足平行条件的典型关节为关节1,不满足平行条件的典型关节为关节2、关节3。
黏性摩擦力矩和关节转速成正比,可以根据不同关节转速下的摩擦力矩拟合出黏性摩擦系数。笔者以关节2为例,使用多组关节匀速转动轨迹进行黏性摩擦系数的拟合。
第一步,只转动关节2,其它关节锁定,测量50组不同速度下不同角度位置的摩擦力矩与重力矩。
第二步,根据角度位置,使50组不同速度下的摩擦力矩一一对应,按角度位置重新分为若干组,每组中有50个不同速度的摩擦力矩。
第三步,关节2相同角度位置下的重力矩是相同的,所以库仑摩擦也是相同的,可以看成一个常数。摩擦力矩的变化是由于角速度的不同导致黏性摩擦变化而引起的,对此有:
(15)
第四步,根据式(15),应用最小二乘法,将黏性摩擦系数σ拟合出。若干组角度位置可以拟合出若干结果,进而求得所有结果的平均值。
关节2向一个方向匀速转动时,关节2的黏性摩擦系数是不变的,为常数,而由于角度位置不同,由式(14)可得关节2的重力矩τg在变化,也就是动态力矩τd在变化。由此,根据式(6)和拟合出的黏性摩擦系数,可以求出库仑摩擦常数fc和库仑摩擦动态力矩因数μ。
(16)
将关节2的匀速轨迹运动学参数、摩擦力矩和黏性摩擦系数代入式(16),应用最小二乘法,计算出关节2的库仑摩擦常数fc和库仑摩擦动态力矩因数μ。基于50组匀速轨迹,可以计算出50组库仑摩擦数据。
6 连接组合体惯性参数辨识方法
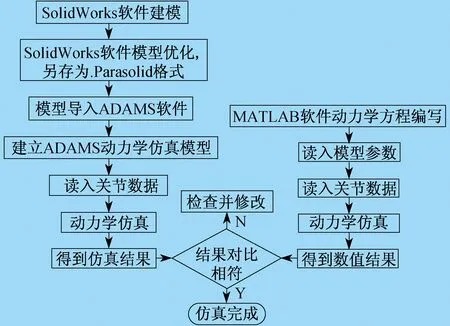
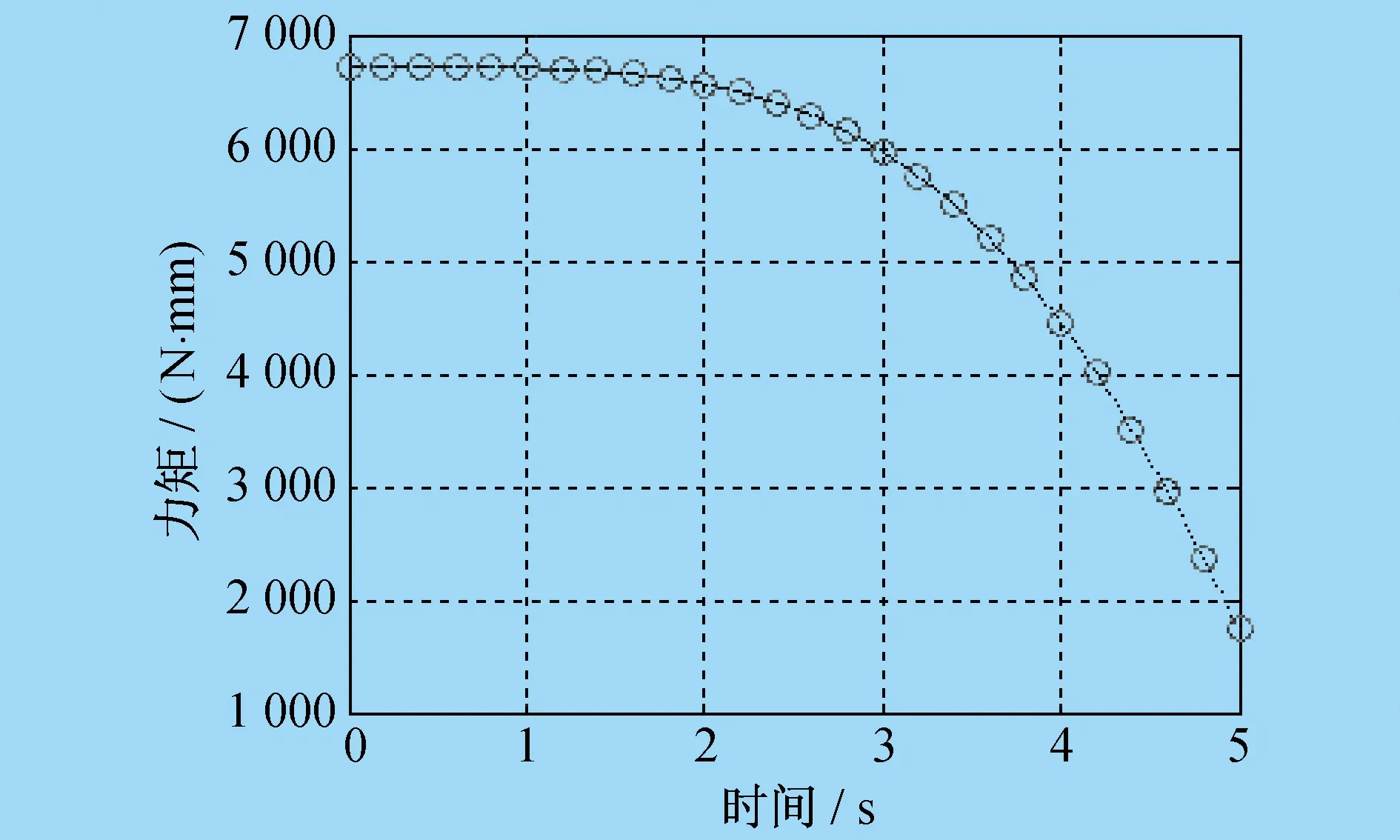
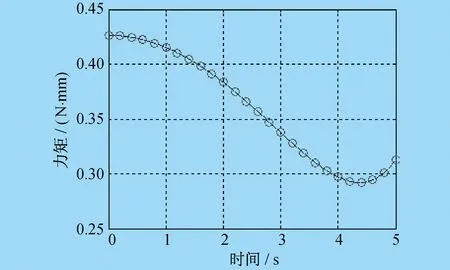
协作机器人机械臂i的十个惯性参数在关节力矩τi中,只有(iIxx,iIxy,iIxz,iIyy,iIyz,iIzz,iHx,iHy)可辨识,所对应的最小参数集向量ipb=[iIxx-iIyy,iIxy,iIxz,iIyz,iIzz,iHx,iHy],这七个独立参数可在与关节i不平行的关节j(j 所谓连接组合体,就是指将串联机器人的关节i+1至关节n锁定,这样机械臂i至机械臂n都可以看作一个整体,记为连接组合体I。同理,关节i至关节n锁定,机械臂i-1至机械臂n都可以看作一个整体,记为连接组合体I-1,依次类推。在笔者研究中,左上标I表示连接组合体的参数,左上标i表示单个机械臂的参数,两者是关于同一个关节的两种不同表示。将第I个连接组合体的独立参数集表示为IpB=[IIxx-IIyy,IIxy,IIxz,IIyz,IIzz,IHx,IHy],将剩余参数集表示为IpR=[IHz,mI,IIyy]。mI为连杆组合体I的质量,IpB可由第i个关节力矩τi辨识,而剩余参数集IpR必须通过其它关节力矩来辨识。在τi-1中,参数IpR与i-1pB不相互独立,两者组合为最小参数集,最小参数集可由相邻连接组合体的参数来表示。 基于以上分析,惯性参数辨识总体而言分为两步。 第一步,由τi辨识连接组合体I的参数IpB。 τi-τif=IcBIpB (17) 式中:τif为第i个关节的摩擦力矩;IcB为连接组合体I惯性参数的因数向量。 IcB可以由机器人运动学参数求得。对式(17)应用最小二乘法,即可解出辨识参数IpB: IpB=[IcBTIcB]-1IcBT(τi-τif) (18) 为了由组合体参数正确求出单个机械臂的参数,需要有关节锁定时各关节的相对转角。为方便计算,一般将关节锁定在零位。 第一步结束后,所有关节所对应的连接组合体参数IpB均已辩识出。第二步,可以通过相邻连接组合体的参数I+1pR、IpB求出单个机械臂的最小参数集组合值ipb。文献[9]和文献[10]给出了求解公式,但是所给出的求解公式较难理解,且没有给出在不同连杆坐标系中的变换过程。因为组合体连杆I-1是由单个连杆i-1和组合体连杆I组成的,所以笔者根据不同坐标系之间惯性张量的平行轴定理和旋转变换定理得出相邻连接组合体的参数I+1pR、IpB,再求出单个机械臂的最小参数集组合值ipb。 (19) (20) mi-1=mI-1-mI (21) 式(19)至式(21)中,参数I-1H、IH、I-1I、II均已辩识出。i-1ri为结构的几何参数,是已知值。mI是IpR中的参数,此时是未知的,也是待辨识的。i-1Izz需要由I-1Izz、IIyy求得,而i-1Hx需要由I-1Hx、IHz求得。此时IIyy、IHz是待辨识的,因此无法求出i-1pb具体数值,只能将i-1H、i-1I,即参数i-1pb表示为待辨识参数IpR的函数。这样,通过式(19)至式(21)就可以求出i-1pb各参数与I-1pB、IpR的关系。 动力学参数辨识正确与否,最直接的验证方法是对测量力矩与所建立的动力学模型计算力矩进行对比。笔者应用ADAMS软件对协作机器人进行动力学仿真,输出力矩为仿真力矩,并使用辨识出的动力学参数在MATLAB软件中建立数学模型,对两者进行对比。仿真验证流程如图2所示。 图2 仿真验证流程 应用牛顿-欧拉递推法对协作机器人进行动力学分析,并采用SolidWorks三维设计软件及ADAMS动力学仿真软件联合建立接近实际的协作机器人动力学仿真模型,得到动力学仿真结果。将ADAMS软件仿真结果与MATLAB软件数学模型计算结果绘制为性能曲线,如图3至图8所示。图3中,红圈为ADAMS软件仿真结果,蓝点为MATLAB软件计算结果,可以看出两者完全吻合,验证了笔者所述协作机器人动力学参数辨识方法的正确性,可以为协作机器人实现拖动示教和碰撞检测功能提供依据。 图3 关节1仿真验证对比 图4 关节2仿真验证对比 图5 关节3仿真验证对比 图6 关节4仿真验证对比 图7 关节5仿真验证对比 图8 关节6仿真验证对比 笔者对协作机器人动力学参数的辨识方法进行了研究,提出了基于连接组合体的辨识方法,建立应用惯性参数组合值的动力学模型,对机器人的关节摩擦进行分析。 通过ADAMS软件建立动力学仿真模型,将仿真结果与MATLAB软件数学模型计算结果进行对比,验证了所采用的参数辨识方法的正确性。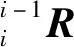
7 仿真验证
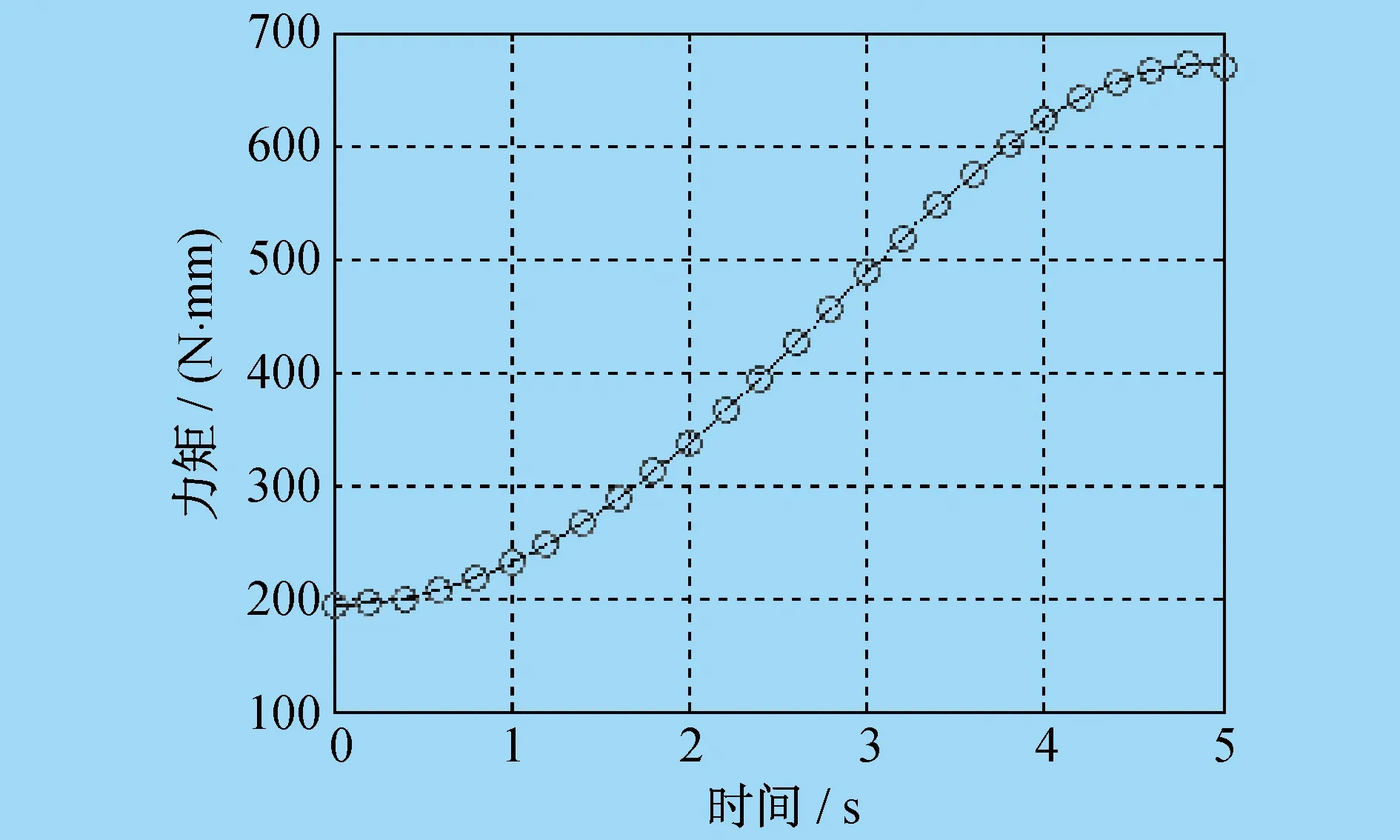
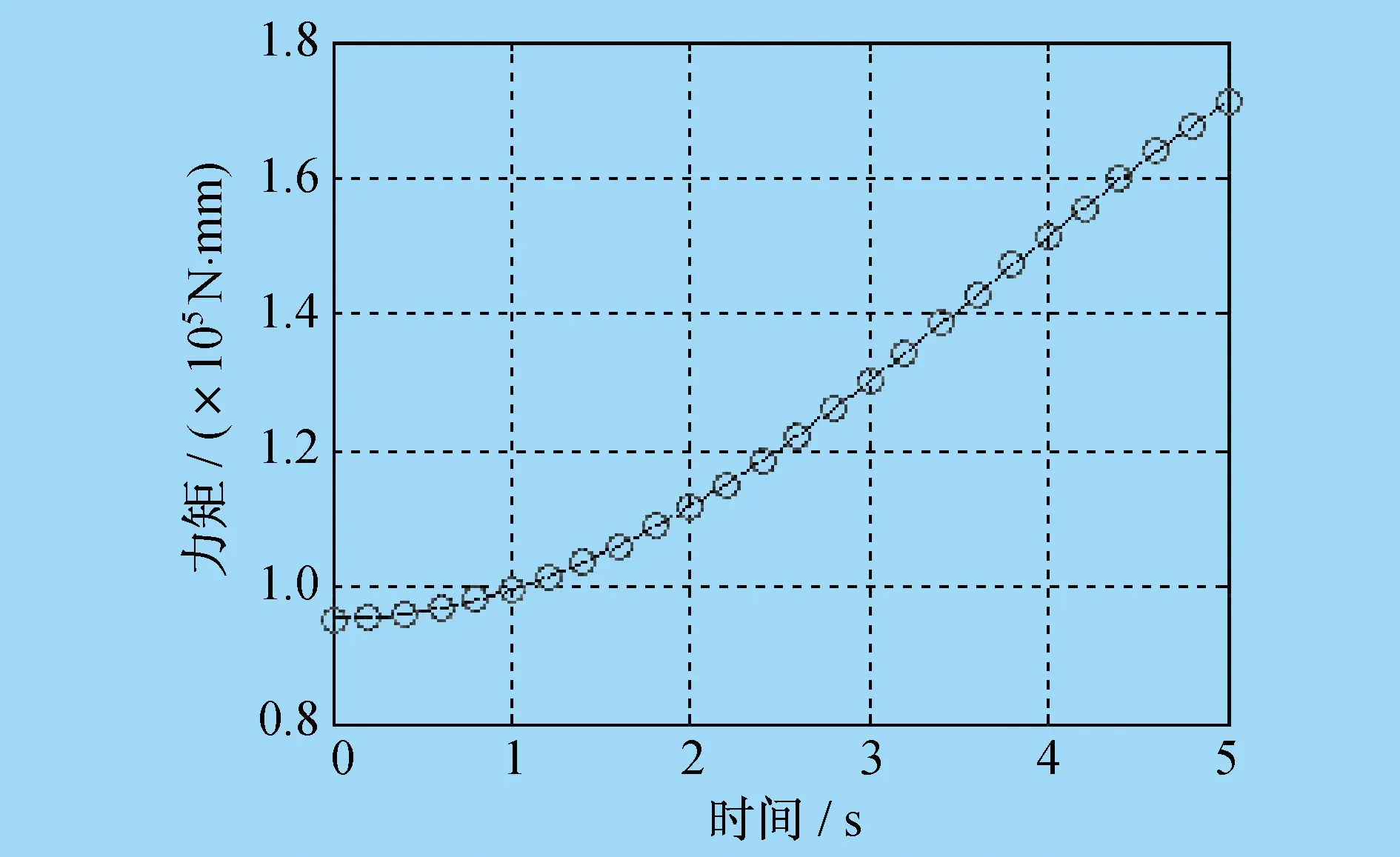
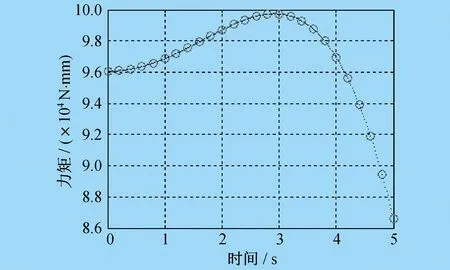
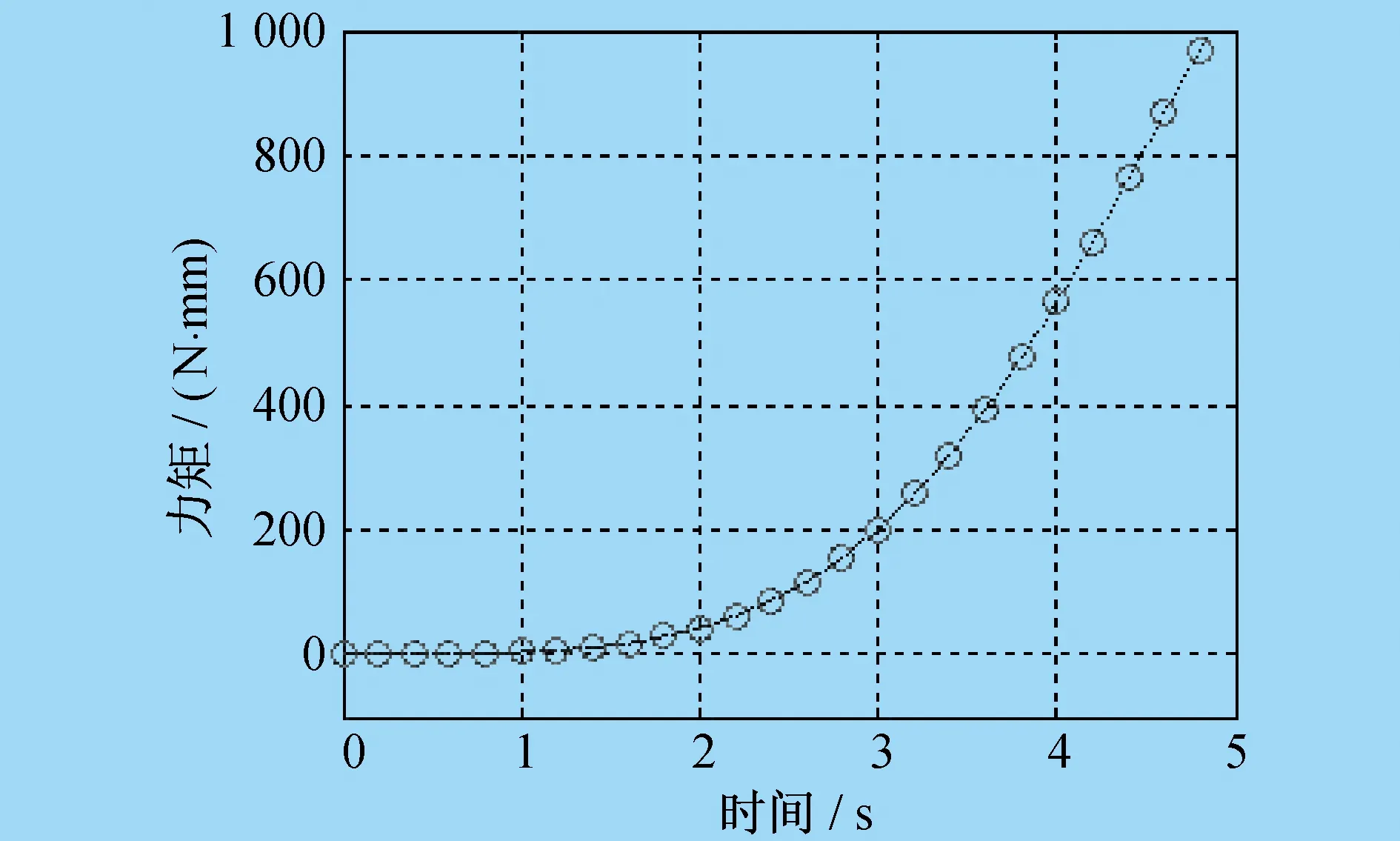
8 结束语
