DOA估计经典MUSIC算法性能分析
2019-12-26陈鹏年温宗周李丽敏
陈鹏年,温宗周,李丽敏,郭 伏
(西安工程大学电子信息学院,西安710600)
1 引 言
波达方向(Direction of Arrival, DOA)估计是阵列信号处理领域的重要研究方向,在雷达、声纳、通信、导航等领域有着广阔的应用前景[1]。现有的高分辨率波达方向估计算法,包括基于子空间分解的波达方向估计算法、最大似然波达方向估计算法以及MVDR 波达方向估计算法等。然而这些算法都不同程度存在计算复杂度高、实时性差等问题,限制了其在实际工程环境中的广泛应用[2]。 刘团宁在文献[2]中,基于子空间分解的波达方向估计算法,提出了利用根值最小范数算法进行改进后的一种基于实数多项式的根值最小范数算法,该算法的主要思想是利用保角变换技术将复数多项式转换为实数多项式,从而减小了计算量,并略为提高了估计精度。袁熹提出了一种最大似然算法在动态DOA估计中的应用方案,针对信源方向时变的情况,提出了一种基于最大似然算法的动态DOA估计方法[3]。
利用处于不同位置的阵列天线接受来自不同方位信号源的信号,并计算信号源的波达方向,是阵列信号研究中的一个重要课题,目前已成果丰硕。波达方向估计经典算法有例如MEM、MVM、MUSIC 以及ESPRIT 等,经过实际中的应用,已不断发展完善。在此主要分析用于DOA估计的经典多重信号分类算法(Multiple Signal Classification, MUSIC),并针对不同条件下MUSIC 算法的性能进行MATLAB 仿真和分析。
2 DOA估计及MUSIC 算法介绍
2.1 DOA估计技术
DOA估计技术是近20 年以来发展起来的一门新型信号处理技术,属于阵列信号处理的一个重要分支[4]。波达方向估计又称为角谱估计(Angle spectral estimation)或波达角(Angle of Arrival, AOA)估计。一个信源有很多可能的传播路径和到达角。如果几个发射机同时工作,每个信源在接收机处形成潜在的多径分量。因此,接收天线能估计出这些到达角就显得很重要。估计的最终目的是判断出哪个发射机在工作以及发射机所处的方向,简单来说就是利用己方雷达接收来自目标发射机的来波方向进行估计,在物理上仍是利用了电磁波的直线传播原理。
通过测量辐射信号的波达方向或波达角来估测辐射源位置, 理论上这种估计只需要两个接收阵元就能达到目的,但在现实中,由于受到角度分辨率、多径和噪声等因素限制,所需阵元通常要多于两个。
DOA 定位技术原理是利用接收机处的阵列天线和波达方向估计技术来确定一个从接收机到信源的波达方向线,即为方向线(LOB),最终利用多个接收机估计的DOA 进行三角测量,方向线的交点就是信源的估计位置。
2.2 MUSIC 算法
多重信号分类算法的基本原理是把阵列输出数据的协方差矩阵进行特征分解,得到与信号分量相对应的信号子空间和与信号分量正交的噪声子空间,然后利用两个子空间的正交性实现信号的入射方向估计。由于MUSIC 算法在特定的条件下具有很高的分辨力、估计精度及稳定性,从而吸引了大量的学者对其进行深入的研究和分析。总的来说,MUSIC算法用于阵列的波达方向估计,有以下一些突出的优点:
1) 多信号同时测向能力;
2) 高精度测向;
3) 对天线波束内信号的高分辨测向;
4) 可适用于短数据情况;
5) 采用高速处理技术后可实现实时处理。
设某个天线阵列具有M 个阵元,且阵元按照等距直线排列,相邻两个阵元之间的距离为d,天线阵接收到的谐波信号[5]即为si,其中i=1,2,…, p,到达每个阵元的波达方向角为θi(i=1,2,…, p),其中p 为远场信号的个数,模型如图1 所示。
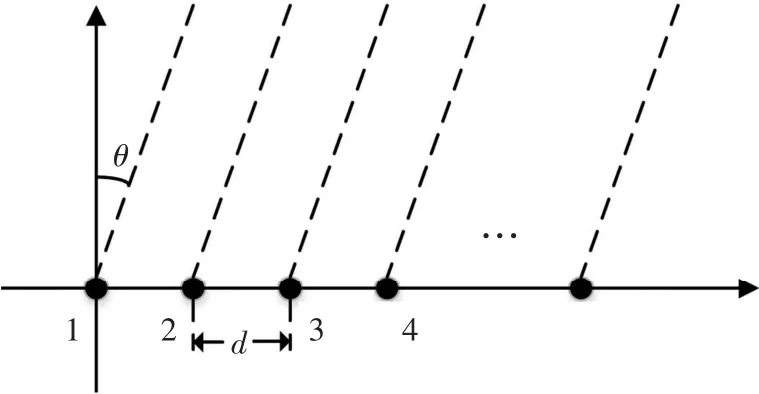
图1 等间距线性天线阵列
因此,第k 个阵元接收到的第i 个信号即可表示为:
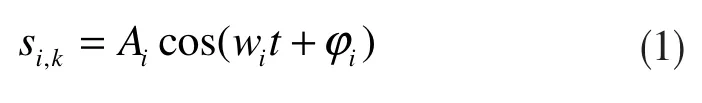
由于信号到第k+l 个阵元的传播距离比到第k个长,第k+l 个阵元接收的信号与第k 个阵元接收的信号之间的相位差为[6]:

其中β=2π/λ 是相位传播因子,λ 表示波长。因此,信号si到M 个阵元的相位差所组成的向量为[7]:
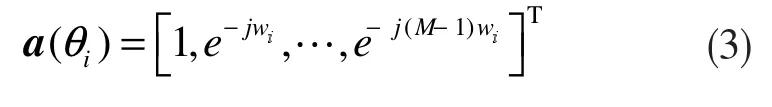
因此,当有p 个信号位于远场时,且p 不大于M,则该等距直线阵上各阵元在观测加性高斯白噪声(Additive Gaussian White Noise, AWGN)下所接收到的信号为:
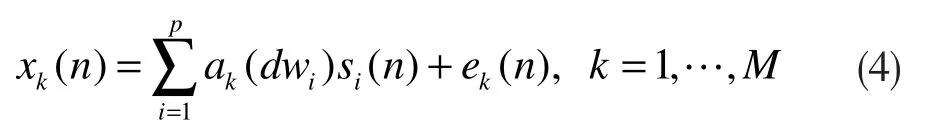
用向量形式表示为:
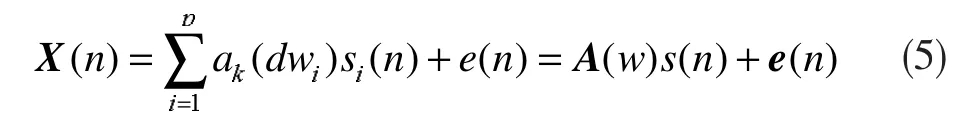
其中:
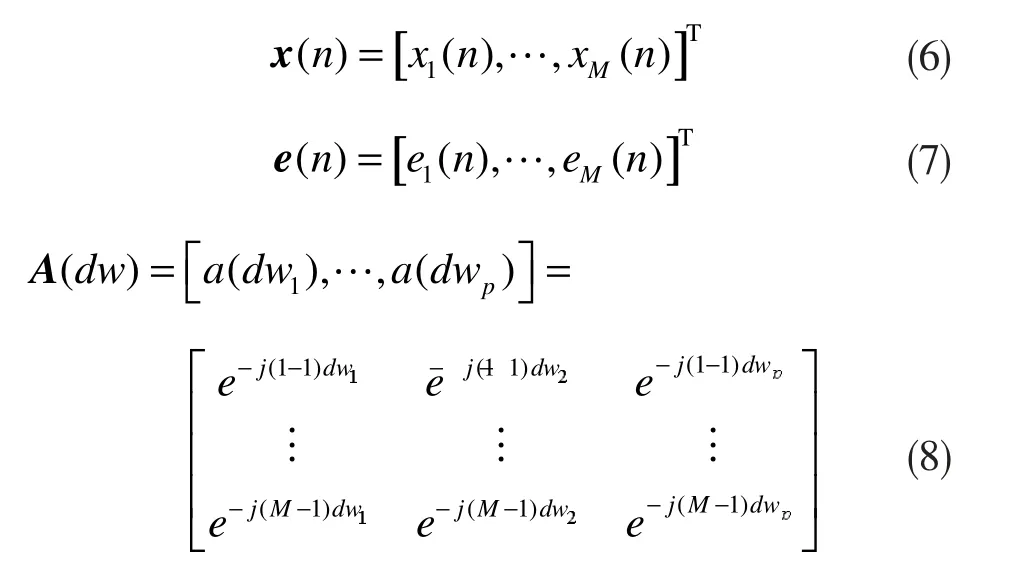
在阵列信号处理中,一次采样成为一次快拍,假定在每个阵元上共观测到N 次快拍的接受信号[8]为X1(1), X2(2), …, Xn(n)。考虑使N 次快拍的输出能量最小,即:
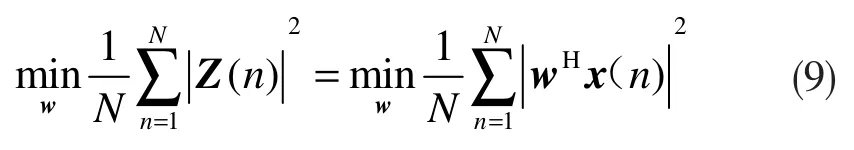
设计权向量w 的这一准则称为最小输出能量(MOE)准则,它在通信信号处理、雷达信号处理等领域有着重要的应用[9]。令:
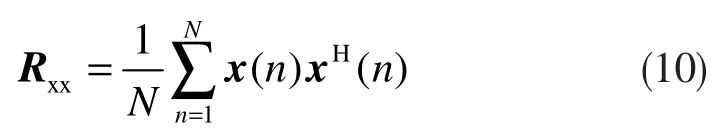
经过推导可以得出一种类似于功率谱的函数:
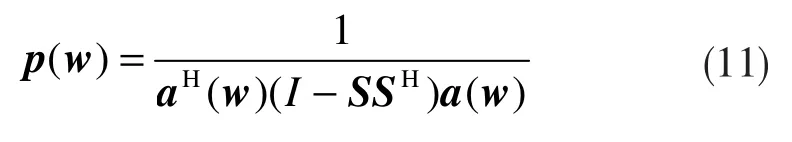
以上的公式(6)被称为信号子空间算法,相应的下式被称为噪声子空间算法:
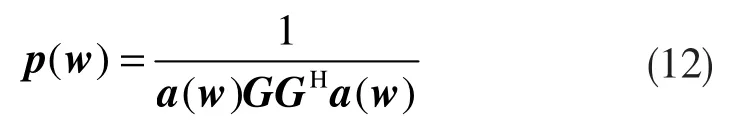
2.3 MUSIC 算法计算步骤
要完成MUSIC 算法的计算,首先要利用阵列所接收的L 快拍数据,得到数据的协方差矩阵的估计值:
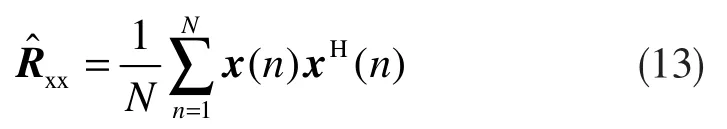
再根据下式进行谱峰搜索:
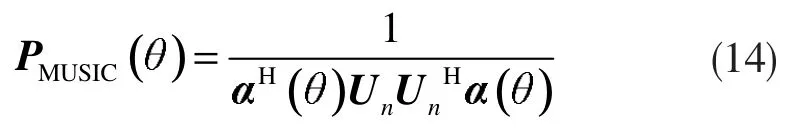
从中找出极大值所对应的角度, 它即是入射信号的角度。至此MUSIC 算法计算完成。
3 MUSIC 算法的MATLAB 仿真分析
运用MATLAB 2018 软件对不同情况下MUSIC算法的性能进行仿真分析,观察不同因素造成的影响。
3.1 阵元数对算法性能的影响
当信源为3,且入射角为-60°、20°、50°,波长为λ/2 时,不同阵元数对MUSIC 算法性能的影响如图2 所示。在仿真中,原始阵元数为8,信源为3,入射角为-60°、20°、50°,波长为λ/2。
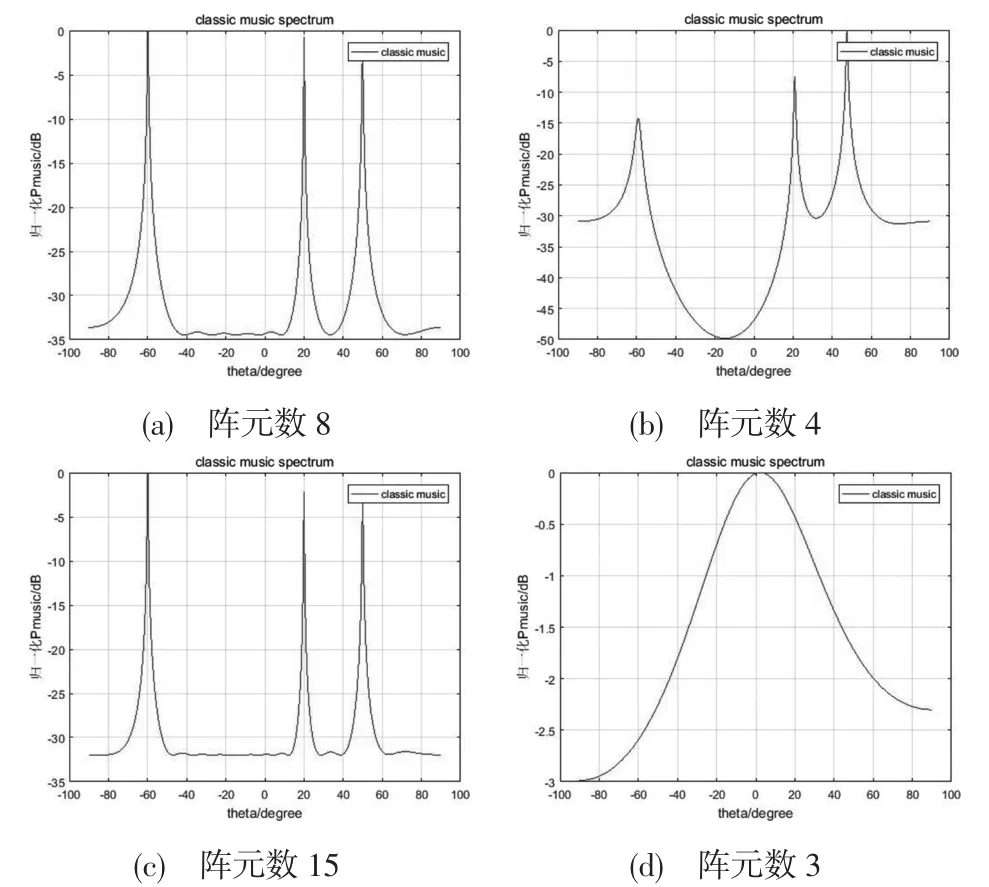
图2 不同阵元数对MUSIC 的影响
可以得出结论:当阵元数为15(大于原始阵元数)时,对入射角的估计更准确;当阵元数为4(小于原始阵元),可以大致反映入射角,但效果不佳;当阵元数为3(等于信源数)时,MUSIC 算法已不能反映信源入射角。
3.2 阵元间距对算法性能的影响
当入射角为-60°、20°、50°,阵元数都为8 时,不同的阵元间距对MUSIC 算法性能的影响如图3 所示。
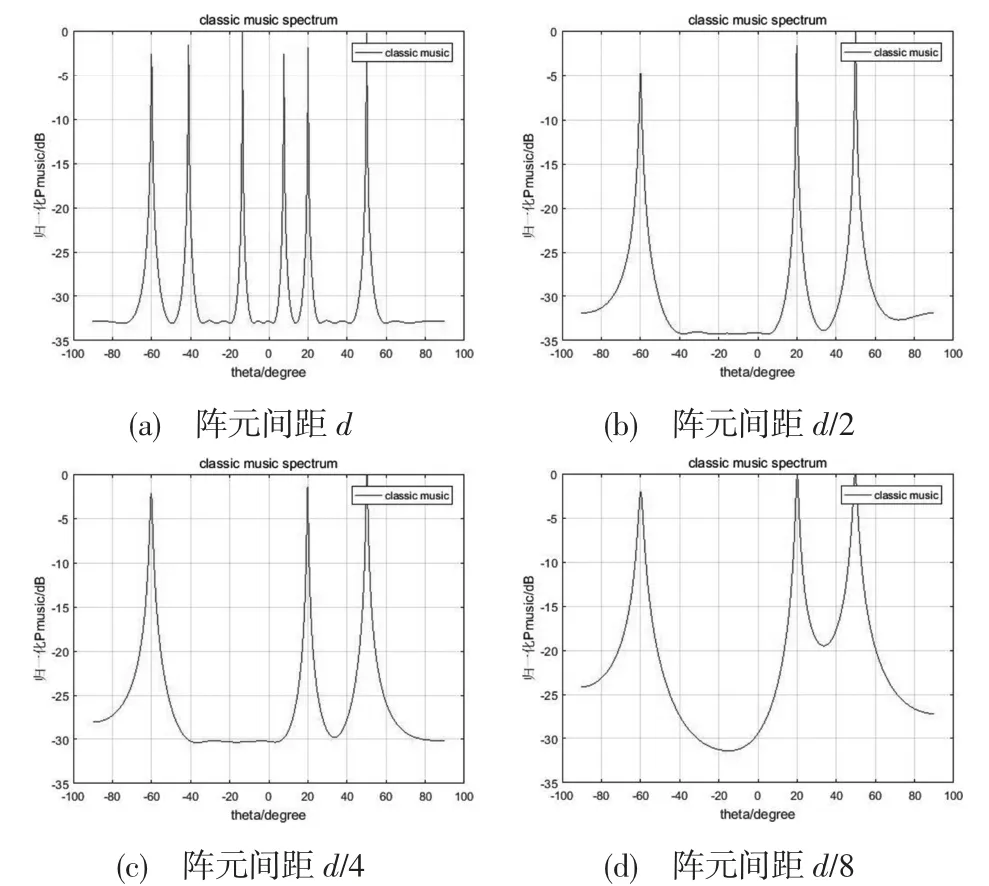
图3 不同阵元间距对MUSIC 的影响
可以得出结论:当阵元间距为d(大于原始间距)时,图中出现伪峰,不能反映信源入射角的方向,如图3(a)所示;当阵元间距为d/2(即半波长)时,估计效果较好,如图3(b)所示;当阵元间距为d/4 和d/8 时,可以反映信源入射角,但效果相对较差,如图3(c)、3(d)所示。
3.3 信源入射角对算法性能的影响
当阵元数为8,阵元间距为λ/2 时,仿真结果如图4(a),可以看出,在信源入射角为-60°、20°、22°时,在一个峰中出现了两个小尖峰,表明有两个信源叠加;其他几种入射角的仿真情况如图4(b)、4(c)、4(d)所示,可见其中明显只有一个尖峰,表明两个信源已趋于完全叠加。因此可得出结论:当信源入射角相接近时,MUSIC 算法比较难以区分入射角度,仿真图上的谱线已不能反映入射角度。
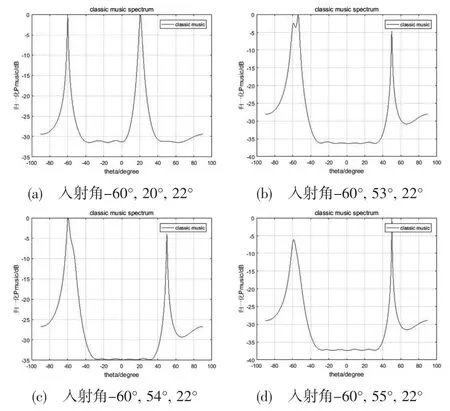
图4 不同信源入射角对MUSIC 的影响
4 结 束 语
波达方向估计测量技术是一种多元天线结合现代信号处理技术的新型测量技术,MUSIC 算法的提出意味着波达方向估计技术向实际应用迈出了重要一步。通过改变阵元数,阵元间距,信源入射角对MUSIC 算法的性能进行仿真分析,证实MUSIC算法有很高的分辨能力,但需要十分精确的阵列校准;其精确度与阵元数阵元间距有着密切的关系;当入射角过于接近,传统的MUSIC 算法失效。这些结论可为DOA 技术的实际应用提供参考。
