基于SVD的陀螺阵列异常诊断及识别方法

杜滨瀚，石志勇，宋金龙

(陆军工程大学石家庄校区，河北 石家庄 050003)

MEMS陀螺具有制造成本低、体积小、质量小、运行功耗低、集成度高、信号处理简单等诸多优点，但其测量精度和稳定性相比于传统惯性敏感器件还有着较大的差距，目前普遍使用阵列技术对其缺点进行改进。陀螺阵列是指利用多个陀螺对同一运动过程进行观测，再对各陀螺进行信号分析与数据融合从而提高其精度、可靠性与稳定性。MEMS陀螺在运行过程中会出现不同模式的数据异常，如发生故障或出现野值等，特别是在陀螺阵列中，零部件数量增多，出现数据异常的几率增大。MEMS陀螺阵列中数据异常具有突发性，且工作环境复杂多变，机载计算机性能有限，导航系统实时性要求高，出现异常后人工难以进行干预[1]。因此，简单有效的数据异常处理方法对于MEMS陀螺阵列是至关重要的。

测量数据中的野值是指严重偏离大部分数据所呈现趋势的小部分数据点，即使是高精度测量设备也会有1%～5%甚至20%的数据严重偏离真值[2]，其一般可分为离群点、孤立型野值和斑点型野值[3]。许多学者对导航数据的野值剔除方法做了大量研究[4-7]，目前导航系统中主要有三类剔除野值方法：根据测量数据的统计特性进行判断、通过信息处理和特征提取方法进行判断以及根据新息的统计特性进行判断，文献[4]对3σ准则进行改进，提高了3σ准则的适应性，但仍需在一个周期结束后进行检验，实时性较差；文献[5]利用5个连续实测数据的标准差作为阈值来判断下一个点是否为野值，减少了计算量，提高了实时性，但样本量较小，没有用到观测值所有信息，在动态情况下可信度较低；文献[6]采用双状态χ2检验法,利用野值点的信息进行剔野，但滤波对非线性情况的估计精度较差，容易出现虚警或漏剔情况。以上方法有的计算量大，无法满足实时性要求；有的需要与特定模型结合，适用范围小；有的在实际工作中可信度较低，无法满足高精度导航系统的要求，且大多数方法无法剔除斑点型野值。

MEMS陀螺故障是指整体或部件无法正常工作的状态，可分为瞬时性、间歇性和永久性故障，或分为可恢复型与不可恢复型故障[6,8]。现在主要有四类故障诊断和隔离(FDI)的方法：基于解析模型的方法、基于知识的方法、基于信号处理的方法和基于数据驱动的方法。由于机载计算机性能限制以及对实时性的考虑，基于小波变换、神经网络和信息熵的诊断方法一般不适用于在线故障诊断，目前较成熟的方法有χ2检验法和奇偶空间法，文献[9]中Ren Da对χ2检验法进行改进，采用两个辅助滤波器定期交换校正，同时用两个状态变量单独进行检测，提高了灵敏度；文献[10]提出以速度误差作为依据的判断准则，解决了χ2检验法误差随时间累计的缺点，但由于滤波在动态情况下精度较差，实际使用时存在较大风险；文献[11]设计了导航系统敏感的最优奇偶向量；文献[12]验证了GLT与OPT方法的等效性；文献[13]对SVD方法进行了解耦矩阵的改进，在原方法的基础上进行了单位化和取模的运算，取得了不错的效果。以上方法对阵列陀螺的故障有较好的诊断效果，但无法辨识野值与故障模式，一般是将不同类型的数据异常均视为故障直接隔离，这可能导致误警过多，组合模式切换频繁，系统可用信息丢失，甚至导致输出值断点等问题。

目前陀螺阵列的故障诊断与野值剔除一般采用不同的方法分开进行，这无疑增加了计算机的负担。笔者利用基于SVD的数据异常诊断方法对陀螺阵列中不同模式的异常数据同时进行检测，并定义了新的统计量对数据异常模式进行辨识，对可恢复型故障和斑点型野值有较好的辨识效果，有效地解决了在线剔野可信度不高、实时性差以及故障诊断虚警率高的问题，在一次预处理步骤中对多种数据异常模式进行处理，极大地降低了系统的运算负担。

1 基于SVD的数据异常诊断方法

1.1 基于SVD的数据异常诊断方法

奇异值分解法是陀螺阵列系统中常用的一种FDI方法，是属于奇偶空间方法的一种。其特点是方法简单、计算量小、正检率高、隔离率高，不需要过多先验知识，对系统建模要求低，是一种较好的FDI方法[13]。

基于SVD的数据异常诊断方法基本思路是:根据系统的硬件冗余或解析冗余方程，构造一个奇偶矩阵，通过实际观测量与奇偶矩阵构造奇偶向量与检测函数，从而达到数据异常检测和隔离的目的[12-13]。使用该方法时首先对陀螺阵列的几何配置矩阵进行分解:

(1)

式中，

UH=[U1⋮U2],

(2)

(3)

利用V阵与陀螺阵列的测量数据向量Z计算奇偶向量p:

p=VZ/σ,

(4)

式中，Z是n维的系统测量值矩阵，当陀螺阵列系统出现故障或数据中存在野值时，测量方程可归纳为[13]

Z=Hx+b+ε,

(5)

式中，b为测试数据的n维数据异常向量。若某一陀螺信号存在数据异常，即出现故障或野值时，b中对应的元素不为0，其余元素均为0.通过奇偶向量p构造出数据异常诊断函数与数据异常隔离函数:

FD=pTp,

(6)

(7)

1.2 仿真实验

陀螺采用6陀螺正十二面体配置，利用Simulink搭建单个陀螺动态信号发生器，如图1所示。仅考虑ARW以及RRW两种主要的随机噪声，并假设确定性误差已经得到补偿，采样时间为100 s，采样频率为100 Hz,正弦信号的频率为0.1 rad/s，幅值为10 (°)/s.利用该信号发生器仿真得到6组不同的陀螺动态信号，将这6组信号作为不存在数据异常的原始陀螺信号。

引理1.1[8] 设f是拓扑空间X到拓扑空间Y的连续函数,若B为X的可数既约闭集,则clYf(B)为Y的可数既约闭集。

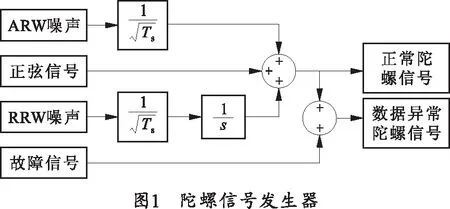
假设陀螺阵列中某陀螺出现数据异常，依次在该陀螺的原始信号上注入野值脉冲、常偏变化故障、噪声增大故障和自行恢复的常偏变化故障，并利用基于SVD的数据异常诊断方法对其进行分析。

图2中数据异常的模式分别为存在野值点、逐渐恶化的常偏变化故障、随机噪声增大故障和可恢复的常偏变化故障。

存在野值点的观测信号是在原始陀螺信号的基础上与野值信号相加得到，野值信号由一个周期为10 s、脉冲宽度为0.05 s、幅值为1的脉冲信号与一组均值为0、方差为3、采样频率为100 Hz的随机信号相乘得到，由此能得到一组从第0 s开始每过10 s就会出现一系列野值点的陀螺信号。其余3种数据异常信号产生方法相同，均是将不同的随机噪声信号作为异常信号与原始信号相加得到，后3种数据异常信号的参数如表1所示。

表1 三类数据异常信号仿真参数

图3为通过SVD方法求解以上4种情况的数据异常诊断函数值FD.

图4为存在数据异常陀螺的隔离函数值FI和正常陀螺的隔离函数值FI，正常陀螺的隔离函数值基本相同，由各陀螺的FI值可知，在出现异常时存在数据异常的陀螺FI值远高于其他正常陀螺。分析图3与图4可知，存在野值点的陀螺信号的FD与FI值仅在野值点处突然增大，其他时刻的FD与FI值较小；常偏变化故障逐渐恶化的陀螺信号在故障发生时刻FD与FI值开始随故障恶化程度逐渐增大；随机噪声增大的故障陀螺信号在故障发生时刻FD与FI值突然增大，比正常值大两个数量级以上；可恢复故障陀螺的FD与FI值先增大至正常值的4～5倍而后回归到正常值。

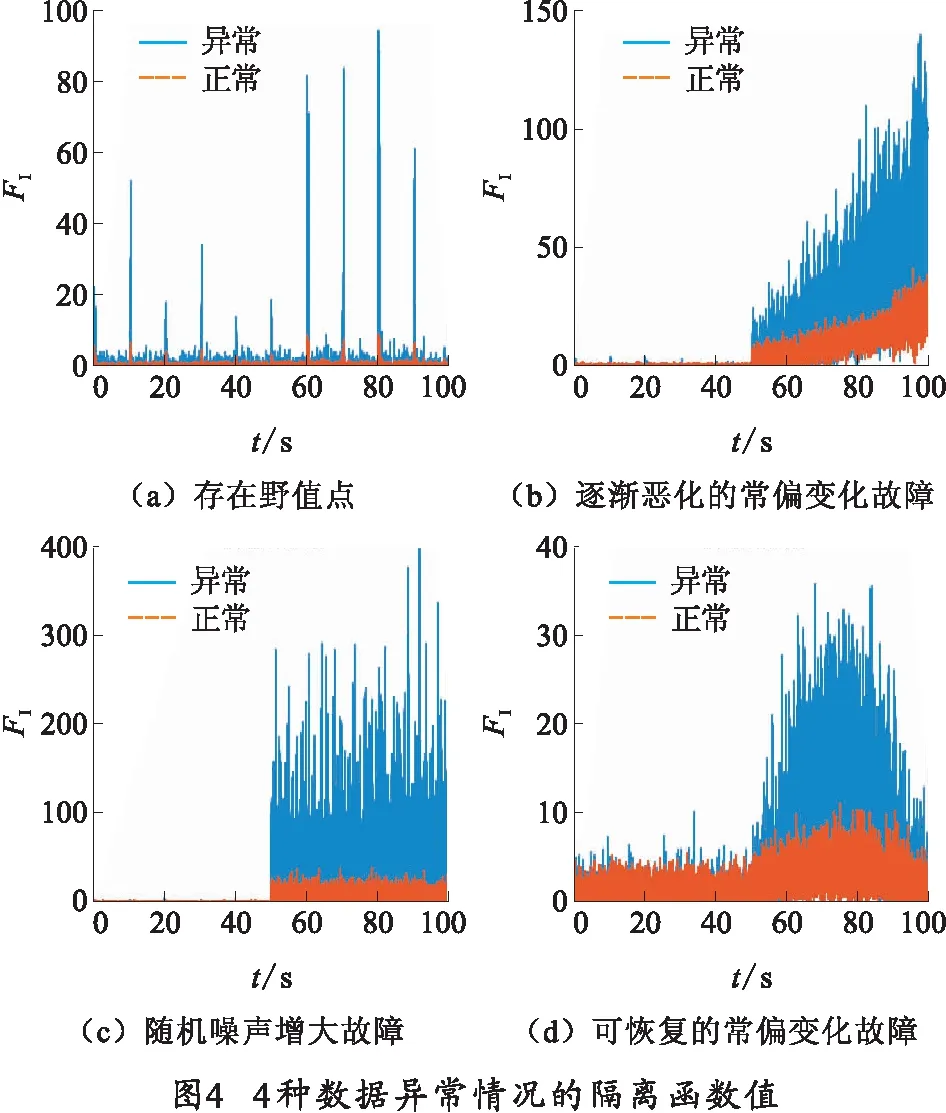
可以看出，基于SVD的数据异常诊断方法求得的FD对数据异常有较好的诊断效果，在几种不同数据异常出现时FD值都超过了预设门限值TD，且FD值的数值大小和变化情况与实际情况相符。而异常陀螺的隔离函数值FI远大于其他正常陀螺，FI同样能够很好地反应出数据异常的恶化程度以及变化趋势。所以能够得出结论：

1)基于SVD的数据异常诊断方法能很好地诊断出各种不同模式的异常数据，并能够真实地反应每种数据异常的特点。

2)故障和野值不同点在于，野值点邻域内其他时刻的FD和FI值均正常，但陀螺故障在一段时间内的FD和FI值均为异常状态。

3)诊断函数值FD和隔离函数值FI均能够较好的反映数据异常的恶化程度以及变化趋势。

2 模式辨识方法

2.1 数据异常模式辨识方法

根据1.2的分析结果，分辨野值点和故障的关键在于邻域内FD和FI异常点的占比不同，分辨可恢复故障与永久性故障的关键在于隔离函数值随时间变化趋势不同。可恢复故障和大型斑点型野值的FD和FI值变化形式相同，均是先增大后恢复到正常值，在之后数据异常的处理步骤中，野值点和可恢复性故障由于持续时间较短，可以通过相同的容错方法进行处理，因此可以将斑点型野值等同于短时间内出现的随机噪声增大故障。经过较长时间才能自行恢复的故障一般和永久性故障处理方法相同，也将其直接进行隔离处理，因此把较长时间才能恢复的故障等同于永久性故障，把经过两个以上诊断周期才能恢复的故障均视作不可恢复故障。

进行数据异常模式辨识前，先对周期内的故障诊断函数值FD进行0.1 s平均处理，每个诊断周期内有n个隔离函数平均值mi(i=1,…,n)，利用最小二乘法对FD进行拟合,得到

A=(NTN)-1NTM,

(8)

(9)

M=[m1,…,mn]T；

(10)

A=[a0,a1,a2]T，

(11)

得到

f(i)=a0+a1i+a2i2.

(12)

定义新的判定值g：

(13)

式中:

m′=f(tn+n);

(14)

(15)

g反映了依照当前诊断周期FD变化趋势下一周期结束时FD的预测值高于或低于诊断门限值的程度。当g<0,则FD预测值大于诊断门限值，该故障可能不会在短时间内消失；当g>0,则FD预测值小于诊断门限值则，该故障就有可能在下一个诊断周期内消失。但为了确保系统尽量不被异常数据数据污染，通过统计的方法确定门限值Tg，只有当g>Tg时才认为该故障恶化程度较低，可以在较短时间内消失，是可恢复故障。若周期内出现的数据异常为野值点，由于野值点属于突变的数据异常，FD的值上升或下降的速率均较大，利用该方法得到的g>>Tg.

Tg可由离差平方和法求得，野值点和可恢复故障的处理方式相同，因此只需设定一个门限值Tg对不可恢复故障和其他模式的数据异常进行区分。设可恢复故障为类Gp，包含了p个元素；永久型故障为类Gq，包含了q个元素；Gp+q为包含Gp和Gq的大类，包含了p+q个元素，由如下公式可求得Tg：

(16)

(17)

(18)

(19)

(20)

(21)

2.2 仿真实验

设计仿真实验，在一段10 s的信号中注入3 000次异常信号，其中1 000次注入野值点，1 000次注入永久故障，1 000次注入可恢复故障，每次数据异常的恶化程度以及持续时间均随机产生。实验求得的g值分布如图5与表2所示。

表2 三类数据异常模式的g值分布

从图5和表2中可以看到，3种不同模式异常数据求得的g值分布范围完全不同，用该方法进行数据异常模式辨识能够取得较好的效果。

利用上述方法确定门限值Tg=7.256，为验证该方法模式识别的准确率，另求出可恢复故障与野值点g值的分界门限值为25.136，在实际工作中没有求解该分界门限值的必要。由存在野值点信号求出的g值基本在25.136以上，1 000次仿真中仅有10次在25.136以下，4次小于门限值Tg，可能是由于随机噪声的影响,FD在诊断周期末期出现上升趋势；由可恢复故障信号求出的g值1 000次仿真中仅有23次小于门限值；而不可恢复故障的g值在1 000次仿真中仅有8次超过门限值。整体来看，3 000次仿真实验中有2 965次辨识正确，正确率达到了98.83%，基本符合预想效果，可以看出该方法对不同模式的数据异常有较好的识别效果。

3 数据异常处理流程

在进行导航参数解算之前进行的预处理步骤增多，导航精度也会相应地提高。但由于运载体上装配的计算机不能和实验室相提并论，同时导航系统对实时性要求极高。所以在进行数据处理时应该力求精简步骤，减少运算量。

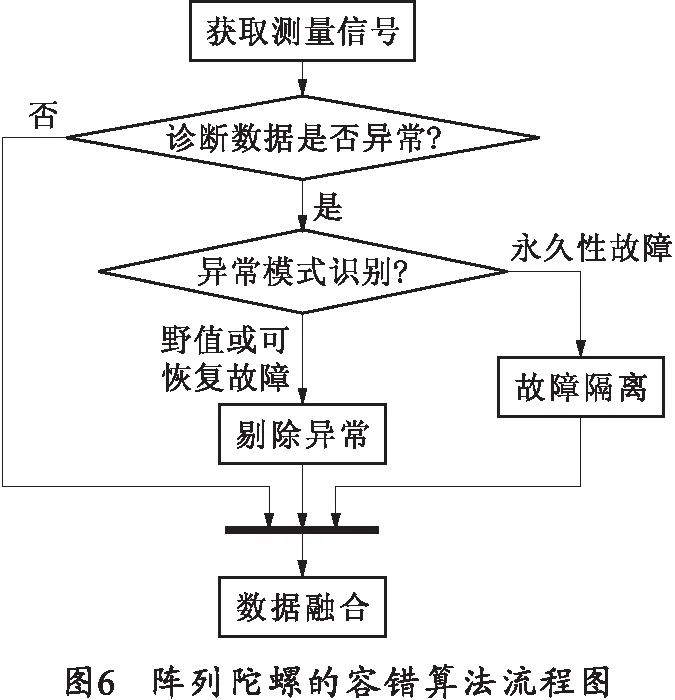
阵列陀螺的容错算法流程图如图6所示。每一时刻在获取观测向量后先利用SVD算法进行诊断，若数据正常则直接进行数据融合，若数据不正常，则进行异常数据隔离，同时诊断周期开始计数。在一个周期结束之前，均把异常数据视为孤立型野值点进行处理，当周期结束时进行数据异常模式辨识，根据不同的数据异常模式进行不同方式的处理。

4 结束语

笔者设计了一种新的阵列陀螺数据预处理方法，验证了基于SVD的新方法对数据异常进行诊断和隔离的有效性，分析了野值点、可恢复性故障和永久性故障三类数据异常通过基于SVD的数据异常诊断方法求得的故障诊断、故障隔离函数值的变化特点，利用其不同的特点定义了新的统计量进行数据异常模式识别，进行了仿真实验。实验结果表明，该方法能准确地对陀螺运行中发生的数据异常进行诊断，能较好地辨识出不同模式的数据异常，极大地减小了异常观测数据对导航系统的影响。将该方法与目前使用较多的剔野方法和故障诊断方法进行比较，现有方法只能判断是否存在某种特定类型的数据异常，无法辨识对多种数据异常类型进行辨识，但如果单看野值诊断成功率，本文方法的成功率高于大多数传统剔野方法，因为大多数传统剔野方法对大型野值斑点无能为力；如果单看故障诊断成功率，本文的方法也不逊于目前大多数故障诊断方法的成功率，且对于正负向故障均能到达接近99%的隔离率。