视觉化表征：让数学问题轻松解决

赵晨鑫 魏佳

【摘要】在数学课堂教学中，用应用题来评估并促进学生数学潜能发展是一种有效手段。视觉化表征能够使学生更好地理解问题，直观地把握问题实质。本文呈现了应用题教学的三种视觉化表征方式：图像表征、图式表征、情境表征。希望通过选择符合小学生思维发展特点的呈现方式来提高数学问题解决能力。

【关键词】小学生  视觉化表征  数学问题解决  思维能力

【中图分类号】G623.5 【文献标识码】A 【文章编号】2095-3089（2019）48-0003-02

1.引言

《义务教育数学课程标准（2011年版）》提出：“运用数学的思维方式进行思考，增强发现和提出问题的能力、分析和解决问题的能力” [1]。在数学课堂教学中，用应用题来评估并促进学生数学潜能发展成为一种有效手段。应用题的解决不仅需要学生具备良好运算能力，也需要有一定的问题表征能力。所谓问题表征能力，就是在应用题的解决过程中，利用画图形、列表格等方法来增加对问题的理解。根据著名数学心理学家Mayer的研究，数学中问题解决的能力主要涵盖以下两个方面：一是对数学问题的表征能力，二是解决计划的执行能力[2]。如果小学生对问题的表征能力相对薄弱，将直接影响数学问题的解决。

2.视觉化表征、问题解决、应用题

2.1视觉化表征促进小学生思维转化

何美萍等人曾探讨视觉化表征及其在数学学习中的作用[3]：视觉化表征描绘了具体的、形象的、直观的意义，便于人们较为快捷地视觉化数学的整体结构和意义，这些表征既是人脑右半球的功能特点，也是右半球发展的外在促进。因此，视觉化表征在数学学习中有着举足轻重的作用。

在小学阶段，学生思维发展的特点主要是抽象逻辑思维在逐步发展，但仍带有很大的具体性，离不开具体事物的支持[4]。因此，在进行纯文字的应用题教学当中，将文字表征模式的应用题转化为图像表征丰富的应用题，不仅可以帮助学生直观地理解题意，而且能够促进思维过渡。美国心理学家维特罗克认为，如果训练学生对他所阅读的东西产生一个类比或表象，他们的理解就会增强，这些表象可能包括图形、图像、表格和图解等[5]。也有专家认为，个体在知识的表征过程当中，影响比较大的是视觉认知。基于此，我们可以认为小学生对图式有着更好的理解力，多利用图式表征能够使小学生更好地明白问题的含义，从而提高解决应用题能力[6]。

如果教师能根据不同年龄段学生运算策略的使用特征及数学思维发展状况，并遵循科学的原则，选择恰当的方式进行教学，不仅可以提高课堂效率，还能有效促进学生数学思维发展。

2.2应用题成为培养问题解决能力的重要载体

应用题是用语言或文字叙述有关事实，反映某种数量关系，并求解未知数量的题目。小学数学应用题通常分为两类：只用加、减、乘、除一步运算进行解答的称简单应用题;需用两步或两步以上运算进行解答的称复合应用题[7]。

应用题——作为小学阶段的重点教学内容，不仅考查了学生们所学习和掌握的数学基本知识与相关技巧，更考查了他们的思考能力以及整合所学知识与技能解决身边现实问题的能力，同时也包含了学生们对于生活中某些问题的态度与情感。正如Reusser所说[8]，应用题是将数学知识与实际情境相结合的问题形式，这种形式有助于帮助学生进行数学思维的建构[9]。但在实际的教学当中我们却发现，学生解决应用题，尤其是纯粹文字应用题的状况却并不理想。

影响问题解决的客观因素之一便是问题的情境。问题情境是指问题呈现的知觉方式。当问题呈现的知觉方式与人们已有的知识经验越接近，问题就越容易解决;相反，如果问题呈现的知觉方式与人们已有的知识经验相差很远，问题解决起来就越困难[10]。而大多数教师在课堂教学中往往会把能力培养形式化，倾向于直接交给学生抽象的數学算法、公式与技巧，而非根据学生的思维发展特点为其创设合理的问题情境来解决问题。这就导致学生不能很好地弥合所学知识与实际问题情境，也不能发挥真正潜能来解决问题。

Morales，Shute，&Pellegrino（1985）[11]通过分析3至6年级学生在解决应用题上的错误后发现：超过67%的错误是“概念性的”而不是“计算性的”。解答错误的学生是因为他们选择了错误的方法而不是计算上失误，这些概念性错误通常只是发生在对问题进行转化的阶段。如果学生不能用正确的数学方法表述应用题中的文字信息（转化），他们将不能正确解决问题;如果能够准确地转化，计算并不是主要的问题[12]。

3.应用题教学的视觉化表征举例

3.1图像表征方式

看图列式计算隶属问题解决范畴。虽有图画做衬托，对于以形象思维为主的小学生来说要准确领悟图所表达的意思，也并不容易。他们对图中信息的解读可能会出现各种各样问题。要通过图片引导学生读懂图，就要从学生对图片的理解入手。开始时，学生可能会停留在仿说跟说的层面，随着说图练习的加强，他们对于问题情境建构就会逐渐清晰起来。

如图1，一道混合运算题目，看箭头的顺序，两张图片要连接在一起看。“湖中原来有4只天鹅在嬉戏，不一会儿飞来了三只天鹅，过了一会儿，又有两只天鹅结伴飞走了，湖中现有多少只天鹅？”其中要强调“飞走”这样的词用减法，“飞来”用加法。当学生反复经历看图——说图——列式这样的步骤，也就等同于经历了自主学习、合作交流，共同探究等过程，在培养了学生思维能力的同时，也在一定程度上帮助学生理解运算过程，提高数学表达能力以及解决实际问题的能力。

3.2图式表征方式

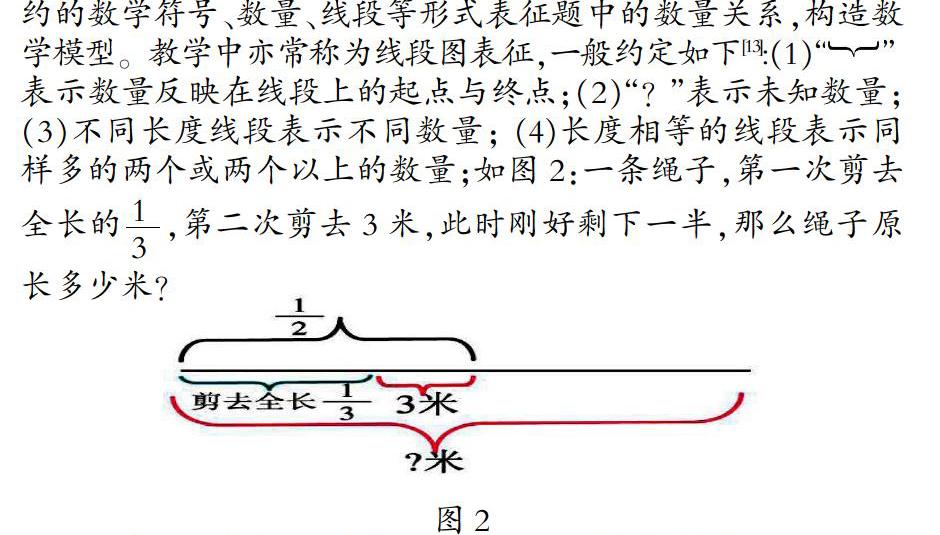
在解决数学问题的过程中，一个关键的影响因素便是对问题的表征能力。学生在面对数学问题时，首先要对问题进行相应的表征，是否具有相应的图式决定着表征的成功与否。图式表征策略是小学生广泛采用的、影响小学生数学问题解决能力的一种表征策略。图式表征是以数学语言和特征为基础，以简约的数学符号、数量、线段等形式表征题中的数量关系，构造数学模型。教学中亦常称为线段图表征，一般约定如下[13]：（1）“     ”    表示数量反映在线段上的起点与终点;（2）“？”表示未知数量;（3）不同长度线段表示不同数量; （4）长度相等的线段表示同样多的两个或两个以上的数量;如图2：一条绳子，第一次剪去全长的，第二次剪去3米，此时刚好剩下一半，那么绳子原长多少米？

用线段图来表征这类问题，它可以有效减弱引入图像或其他元素时造成的认知负荷过大的情形。另外，通过作图，原来题目中文字叙述的数量变得直观，符合小学生形象思维特点，学生一看就明白文字的含义，也就能正确地求解。求解过程中还可保留这些痕迹，其优点在于：这些具体操作活动是进一步开始抽象思考的基础，同时保留具体作图痕迹也便于监控及反思解题过程。

3.3情境表征方式

小学阶段的数学内容多数源自生活，但也包含数学本身的内容。在实际教学过程中，学生们大多被灌输“为了快速解题而解题”的学习思想，而不考虑真实问题情境。这种行为会导致学生们不能理解问题情境的意义，无法将所学知识技巧与生活弥合，不能充分发挥其在日常生活中解决问题的潜力。Kees Hoogland et al.（2018）在语境教学问题表征变化对学生表现的影响这一研究中，通过改变问题表征方式，对来自中小学年龄在10-20岁之间的31，842名学生进行了测试并得出结论：学生在描述问题情境的问题上得分明显较高[14]。在研究中，他们所采用的问题表征方式主要以照片、报纸的标题和手写注释的形式（如图3），来增强模拟的逼真度，追求对现实生活的再现，一定程度上避免了为“尽快得出答案”而专注于计算方法与结果的定势思维。

苹果以 2.5 公斤的袋装出售，一个苹果重157克。袋子里大概有几个苹果？文字表征转换为视觉表征后，问题情境更加真实，加强了学生对问题的知觉性理解。所谓应用题，是要把理论概念应用起来解决真正的问题。问题不仅仅以书面形式存在，更渗透于生活当中。转换问题表征方式，糅合知识与实际经验，才能真正做到将应用题应用于生活。

结束语

小学生，尤其是低段的学生，在实际生活中的经验和知识量是十分有限的，因此对应用题所表达的情境以及某些符号语句都会感到难以理解。这就要求我们依照弗赖登塔尔的数学教学原则[15]，尽量为小学生创设与生活相关的实例——接近生活实际的图像或照片，让小学生容易理解题目文字的意思，引导他们结合已有数学知识经验去解题，以便更好地向抽象思维过渡，从而激发数学学习的潜能，提升数学问题解决的能力。

需要注意的是，我们从认知负荷理论角度来看，在添加图像时，额外的信息会给学生的理解带来额外的认知负荷，从而引发注意分散。基于小学生思维的特点，容易被解决问题的无关因素所吸引，例如，若出示一幅色彩丰富的图片，题意是要学生计算图片中小明手里和地上筐里的苹果共有多少个，而学生可能额外注意到的蓝天、白云、花草树木这些无关因素。因此，在给文字应用题添加视觉化表征时应尽力避免太过复杂的图像，仅呈现从题目文字中所提取出的信息即可。

参考文献：

[1]中华人民共和国教育部.义务教育数学课程标准 （2011年版）.北京：北京师范大学出版社，2011

[2]路海东.小学生数学应用题解决的认知与元认知策略及其训练研究[D]. 东北师范大学，2004

[3]何美萍，唐剑岚，全波.视觉化表征及其在数学学习中的作用[J].内蒙古师范大学学报（教育科学版）.2008（08）

[4]沈德立.小学儿童发展与教育心理学[M].上海：华东师范大学出版社，2003.8

[5]付建中.教育心理学[M].北京：清华大学出版社，2010.8

[6]路海东，董妍.小学生表征数学应用题策略的实验研究[J].心理发展与教育，2003（01）：60-63.

[7]顾明远.教育大辭典（增订合编本）[M].上海：上海教育出版社，1998，20-32.

[8]Reusser K，Stebler R. Every Word Problem Has a Solution—The Social Rationality of Mathematical Modeling in Schools.Learning and Instruction，1997（4）：309-327

[9]陈英和，仲宁宁，赵宏，张小龙.小学2-4年级儿童数学应用题表征策略对其解决不规则问题影响的研究[J].心理科学.2005（06）

[10]张大均.教育心理学（第二版）[M].北京：人民教育出版社，2003.

[11]Morales， R. V.， Shute， V J.，&Pellegrino， J. W. Development differences in understanding and solving simple mathematics word problems. Cognition and lnstruction.1985（2）：41-57.

[12]杨光伟.学生在应用问题解决上的元认知行为表现与信念[D].华东师范大学，2006

[13]张敏铃.小学生运用图式表征进行问题解决的现状研究[J]. 课程教学研究，2017（01）

[14]Kees Hoogland;Jaap de Koning;Arthur Bakker;Birgit E.U. Pepin;Koeno Gravemeijer. Changing representation in contextual mathematical problems from descriptive to depictive： The effect on studentsperformance[J]. Studies in Educational Evaluation， 2018， Vol.58：122-131.

[15]杜剑影.小学数学简单应用题教学策略的研究[D].天津师范大学，2010

作者简介：

赵晨鑫（1996.3.14-），女，汉族，辽宁盘锦人，硕士研究生在读。