基于随机变量状态时序模拟的光伏并网系统概率潮流研究
2019-12-25朱浩祎孙佳琪余维涛王欣然段佳鑫
苑 婷 ,王 俊 ,朱浩祎 ,王 刚 ,张 林 ,孙佳琪 ,余维涛,王欣然,段佳鑫,孟 妍
(1.国网辽宁省电力有限公司 盘锦供电公司,辽宁盘锦 124000;2.沈阳农业大学 信息与电气工程学院,沈阳 100161;3.国网辽宁省电力有限公司 沈阳供电公司,沈阳 110003)
截至2018年末,我国光伏累计装机容量达到174.63GW,稳居世界第一位。光伏发电在缓解能源紧张等方面起到了重要作用,但也为电网的安全稳定运行带来了新的问题[1]。越来越高的光伏并网渗透率使得传统配电网的单向辐射状供电模式被改变的同时,增加了光伏发电的随机性、波动性等各种不确定因素,考虑各种不确定性因素的电力系统概率潮流研究成为近年来学术界的热点问题。严岩等[2-3]针对传统发电机和负荷不确定性问题对传统拉丁超立方抽样法的抽样过程、抽样次数进行改进,并开展研究;鲍海波等[4]基于证据理论研究风电出力和负荷不确定性,提出了一种电力系统概率区间潮流模型和算法;柳志航等[5]综合考虑随机性和模糊性,建立了风电出力和负荷的随机模糊不确定性模型;吴巍等[6-7]在概率潮流计算中考虑了光伏发电相关性对系统的影响,采用改进的Nataf法处理相关随机变量的抽样;周竞等[8]考虑源荷双侧响应变量的概率模型,对基于半不变量法的概率潮流进行改进;田蓓等[9]考虑多个风电场间功率相关性,建立了概率潮流联合分布计算方法;张喆等[10]为准确评估分布式电源出力及负荷不确定性对电网电压的影响,对传统2点估计法进行了改进;任洲洋等[11]考虑了光伏功率和负荷间的相关性,提出了基于Monte Carlo模拟法的概率潮流计算方法;叶林等[12]将高斯混合模型与改进加权最小二乘法相结合,有效简化了求解的复杂程度;肖天颖等[13]研究了考虑风电、光伏发电出力时变相关性的电力系统概率潮流问题。现有文献中鲜有讨论光伏发电功率具有时序的不确定性[14-16]、波动性。针对上述不足,本研究结合对应时间的光伏发电功率预测,开展基于随机变量状态时序模拟的光伏并网系统概率潮流研究,以为电力系统调度、安全稳定运行提供理论指导。
1 基于BP神经网络的光伏发电功率预测
1.1 光伏发电功率影响因素分析
影响光伏发电多少的环境因素主要有辐射强度、温度、风速等。本研究从DKA(desert knowledge australia)太阳能中心获取某光伏电站历史发电、环境等数据用于相关研究。该电站有光伏面板22块,每块额定输出功率250W,总容量为5.5kW,面积共计36.30m2。基于电站数据分析了环境数据与输出功率的关系,其中,太阳辐射强度、环境温度、湿度以及风速与光伏发电输出功率间的相关系数分别为0.9939,0.5032,-0.3861,0.5383,表明存在极显著的相关,具有较强的统计意义。故本研究以太阳辐射强度、环境温度、湿度以及风速4种环境因素作为预测模型的输入变量,忽略其他因素。4种环境因素与光伏输出功率间关系散点图如图1。
1.2 BP神经网络
光伏发电功率预测方法有时间序列法[17]、回归模型法、灰色预测技术、组合预测法、BP神经网络法等。其中,BP神经网络法可对复杂的非线性关系进行较好拟合,本研究采用该方法进行光伏发电功率预测。神经网络是模拟动物大脑神经处理以及记忆信息的方式,由大量相互交叉的单元组成的非线性、自适应的信息处理系统。而BP(back propagation)反向传播网络,则是目前被应用最为广泛的一种神经网络。它的名字源于其处理内部信息网络权值的调整规则,即BP神经网络算法。
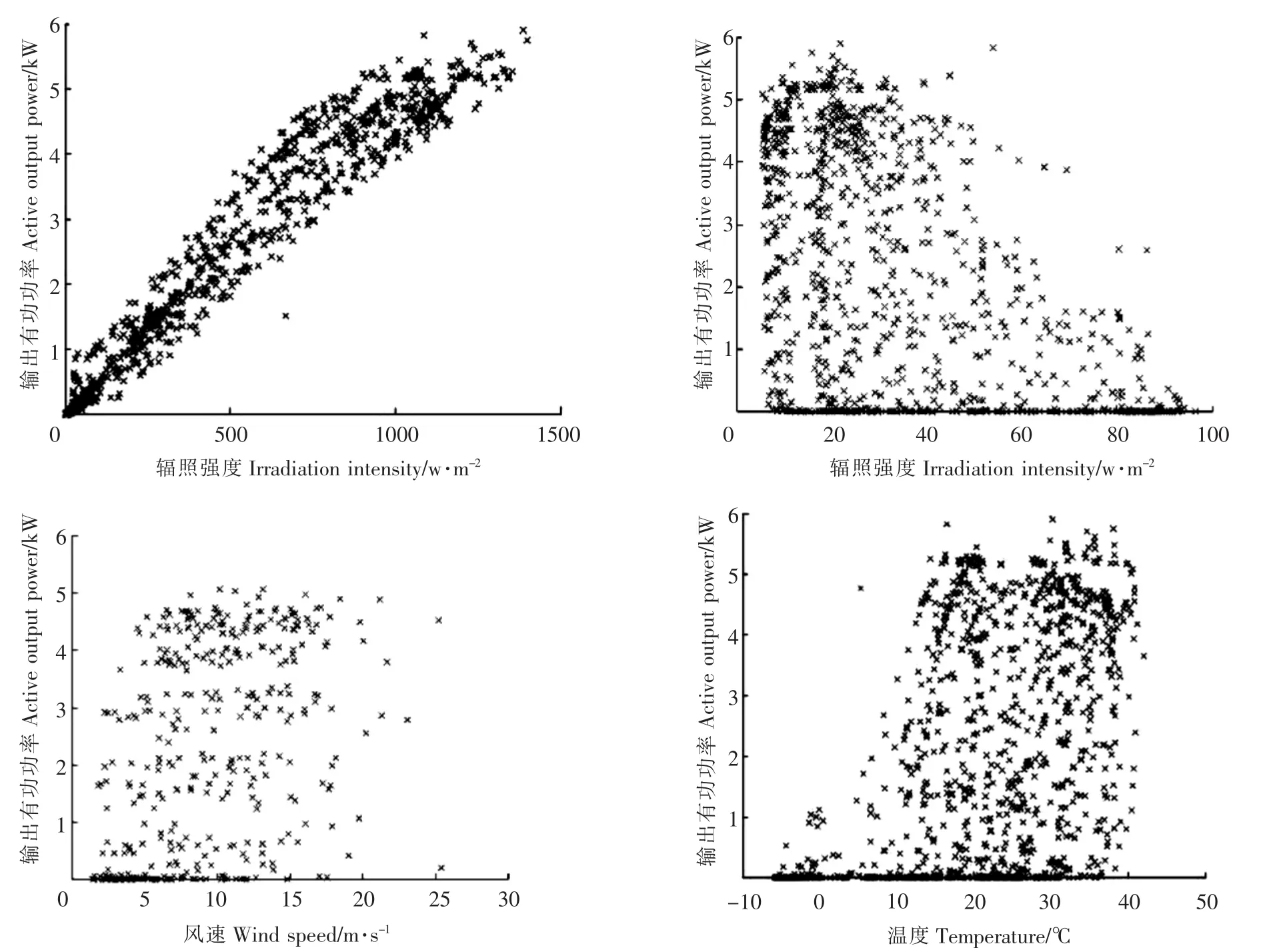
图1 环境因素与光伏输出功率间关系Figure 1 The relationship between environmental factors and photovoltaic output power
本研究以太阳辐射强度、环境温度、湿度以及风速等4种环境因素作为预测模型的输入变量,由此构成四输入一输出的BP神经网络(图2)。其中,x1,x2,x3,x4分别为风速、温度、湿度、辐射强度,y为输出功率。
在三层神经网络当中,中间前层有两个神经元,其输入函数分别为:
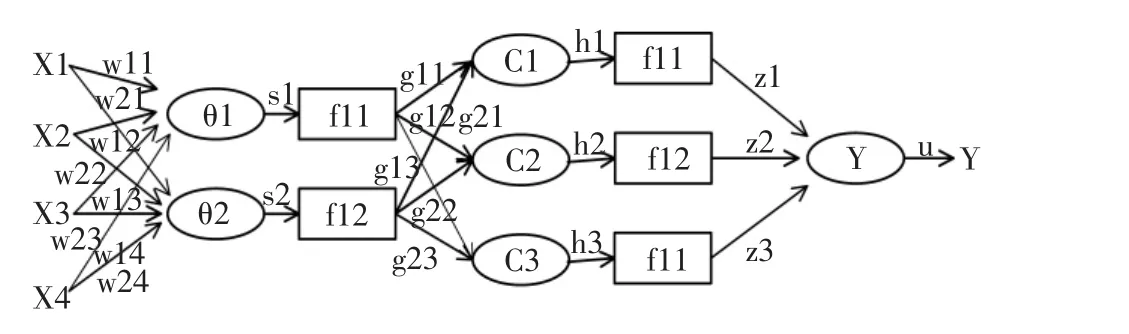
图2 光伏发电功率预测BP网络模型示意图Figure 2 BP network model for photovoltaic power generation prediction

与输入函数相对应的两个输出函数分别为:

中间后层设置有3个神经元,其对应输入函数分别为:

式中:g为权数;c为阈值;h为输入。
3个相应的输出为:

式中:z为中间后层输出。

输出层的输入函数,表示为:关于BP神经网络算法的详实介绍可参考文献[18-19]。
2 基于序贯蒙特卡洛法的电网状态确定
电网中含有诸多元件,任意元件均可能发生故障,元件的个体故障概率、故障时间、修复时间等将影响整个电网运行状态。利用序贯蒙特卡洛法[20]能够模拟电网的时序状态,该方法是基于元件状态持续时间概率分布进行的抽样,其主要步骤为:(1)首先需要设定系统中每个元件的最初状态,假设初始均为正常运行状态;(2)需要研究每个元件在正常运行状态下持续运行时间及每次转换过程持续的时间;(3)在所要计算的时间段内重复步骤(2),并对所有的时间值进行记录分析,既能得到这段时间内的元件的状态变化过程(图3);(4)将单个元件的状态转换过程,按照实际的需求,将其进行排列组合,就可以得到线路,甚至是电网的时序转换图(图4)。
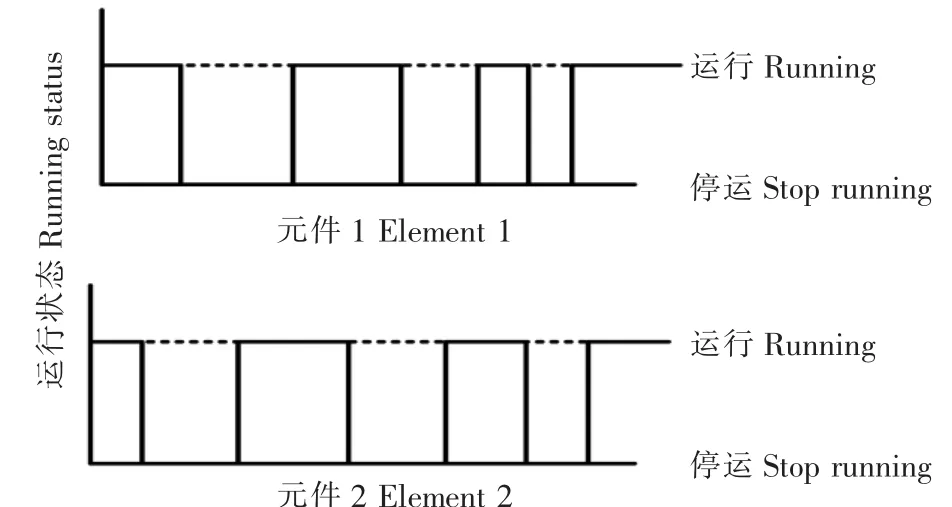
图3 元件运行状态转换过程图Figure 3 Component running state transition process
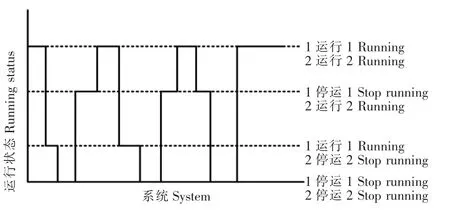
图4 系统状态转移过程Figure 4 System state transition process
3 算例分析
基于IEEE 30节点标准系统开展相关研究,系统结构和参数可参考文献[21]。
3.1 光伏发电功率预测方法有效性验证
利用DKA太阳能中心某电站实际数据开展光伏发电功率短期预测研究。图5为预测功率与实际功率对比图;另外,计算得知,通过3000次的模型训练后,模型的输出值与目标值均方根误差最小值达到约0.000256。可知本研究提出的四输入一输出的BP神经网络适用于光伏发电功率的实际预测。
3.2 考虑光伏接入的电力系统概率潮流研究
假设 IEEE 30 节点系统中节点 3,7,14,21,29 接入分布式光伏电源,容量均为5kW,利用前述光伏发电功率预测方法预测出未来72 h实际光伏出力,在此基础上进行潮流计算。图6显示了光伏接入下未来72h的系统中各节点电压幅值情况。为观察不同光伏出力对节点电压的影响,将预测的光伏输出功率放大100倍并进行潮流计算,各节点电压幅值情况如图7。对比图6可发现光伏出力越大对节点电压影响越大。另外,由图7可知,若电压波动允许上限为10%,则节点26已经超出限值,达到115%,该数值会对电网安全稳定运行带来较大风险,在系统中接入光伏时需要格外注意,应采取有效手段调整该节点电压。图8为未来72h节点电压幅值的均值与初始值(无光伏接入)对比情况。由图8可知,光伏接入可显著提高电网电压水平,改善电能质量。图9为光伏接入后节点6,16,26电压幅值在未来72h的变化情况。由图9可知,光伏的接入对不同节点有不同程度的影响。若能合理的选择光伏接入点及容量,必将能够有效改善电网电能质量。
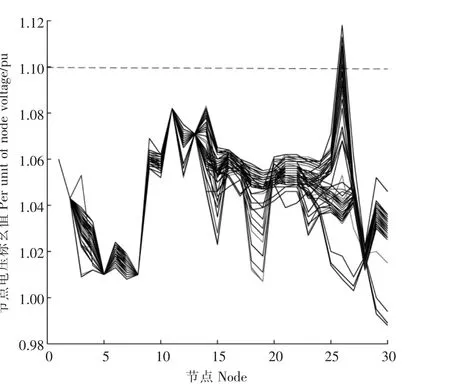
图7 光伏接入下各节点电压幅值Figure 7 Voltage amplitude of each node under PV output increases
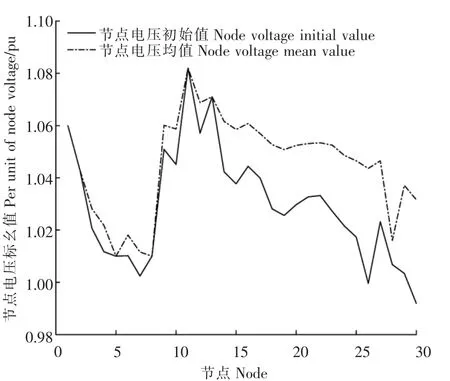
图8 光伏并网前后的节点电压对比Figure 8 Voltage comparison before and after photovoltaic grid connection
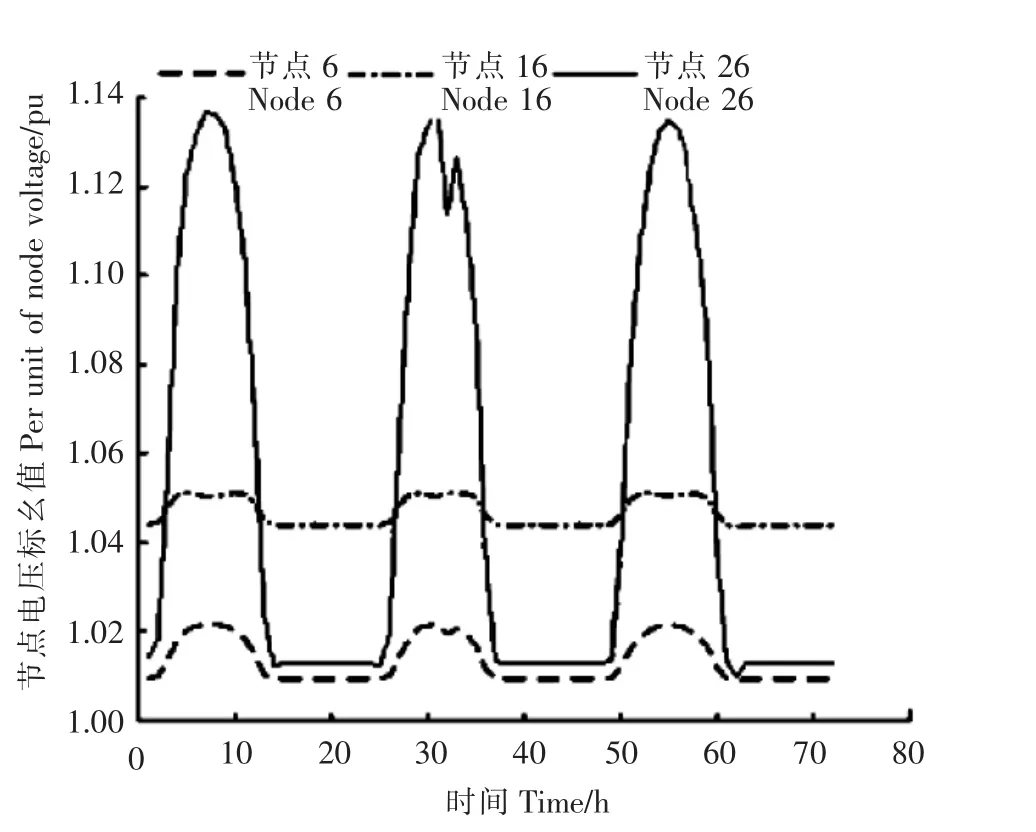
图9 光伏接入下部分节点电压的时序变化Figure 9 Time scries change of voltage at some node
3.3 考虑电网状态时序变化的电力系统概率潮流研究
本研究中考虑线路故障退出对电网状态的影响。设定每条线路的故障概率均为0.01,当线路故障时,故障线路修复平均时间为5h,故修复概率为0.2,假设初始均为正常运行状态,采用时序蒙特卡罗法,可以时序模拟出一段时间内每条线路的运行状态。图10为IEEE 30节点系统中某两条线路在未来72 h的状态。由图10可知,第一条线路在第46h和47h的时候各出现了一次断线故障,第二条线路除了一次较短时间的故障外,在第27 h更有一次持续了将近14 h的故障。
将系统中所有线路状态进行时序组合,即可得到整个电网的时序状态。表1为所有线路在第15h的状态,其中,1表示运行,0表示此线路故障退出。
图11为未来72 h考虑电网状态变化时各节点电压情况;图12为考虑电网状态变化情况下未来72h部分节点电压的时序变化情况。
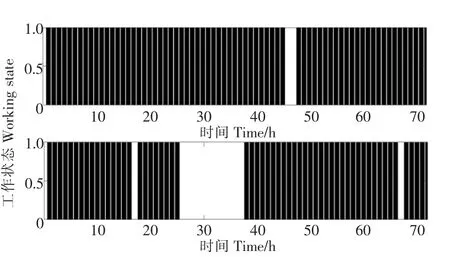
图10 部分线路状态时序模拟Figure 10 Time series simulation of branch state
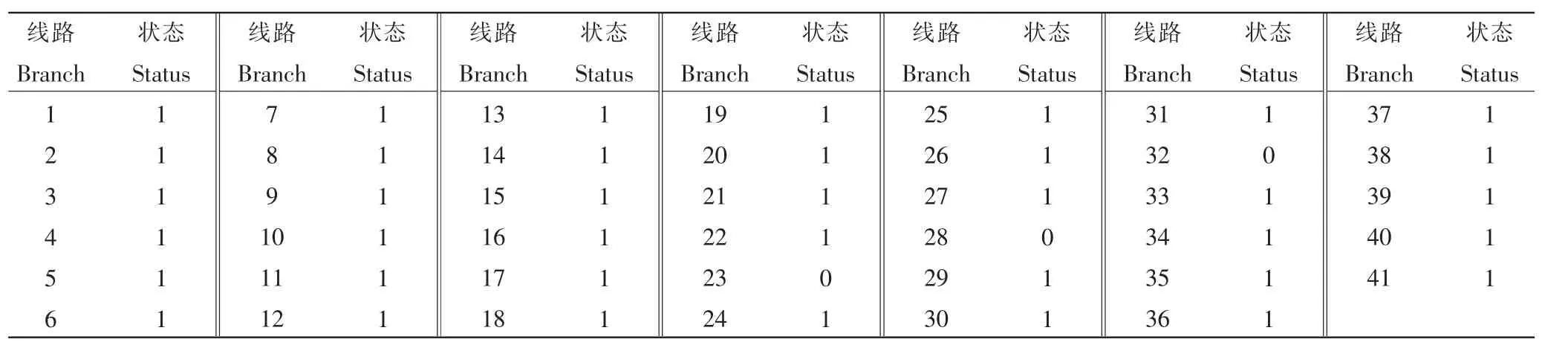
表1 第15 h所有线路状态Table 1 All branch status at 15 hours
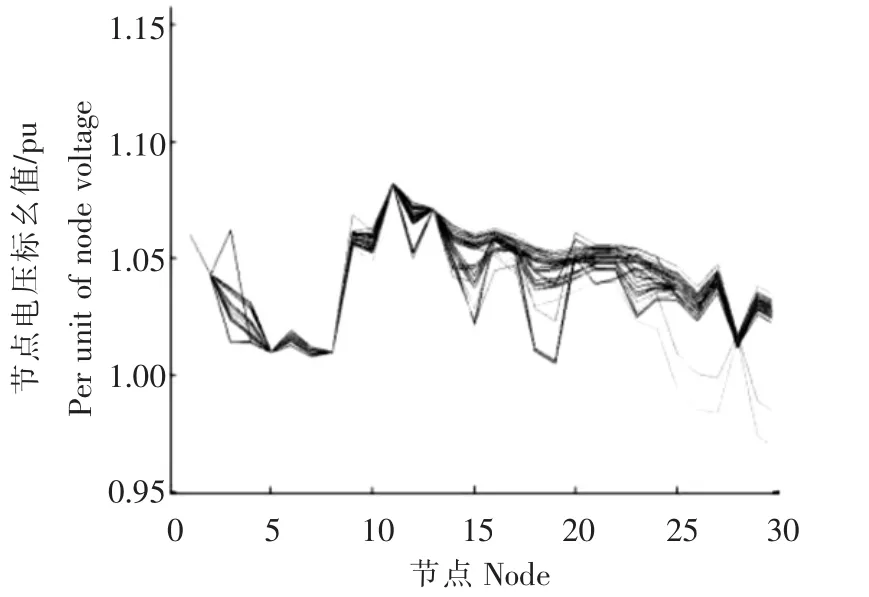
图11 电网状态变化时各节点电压幅值Figure 11 Voltage amplitude of each node when the grid state changes
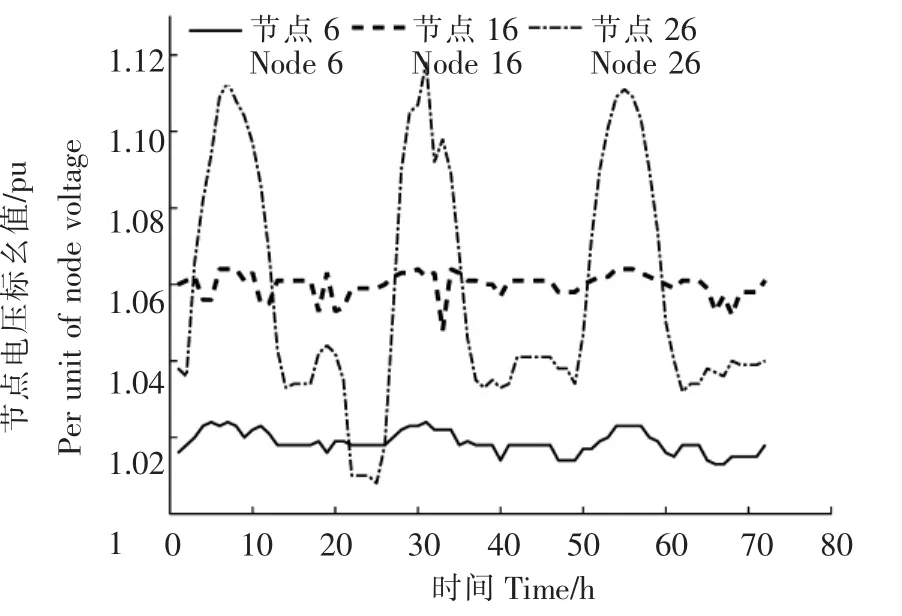
图12 电网状态变化时部分节点电压的时序变化Figure 12 Time series change of voltage at some node when the grid state changes
3.4 考虑光伏接入和电网状态不确定性的电力系统概率潮流研究
图13 为综合考虑光伏输出功率、电网状态的不确定性情况下未来72 h系统中各节点电压变化情况。由图13可知,相比只考虑光伏接入的图7和只考虑电网状态变化的图11,线路各节点的电压波动得更加严重,节点23的峰谷差甚至超过15%。所以,在电力系统潮流计算中综合考虑光伏输出功率、电网状态等随机变量的不确定性非常必要。除了节点电压以外,还可通过节点注入的有功、无功功率等对系统潮流进行分析,得到更为详实的潮流信息(图14)。以此为基础,可分析系统可能出现的风险和薄弱环节,为相关规划、调度等部门的决策提供全面的信息,提升电网的安全水平。
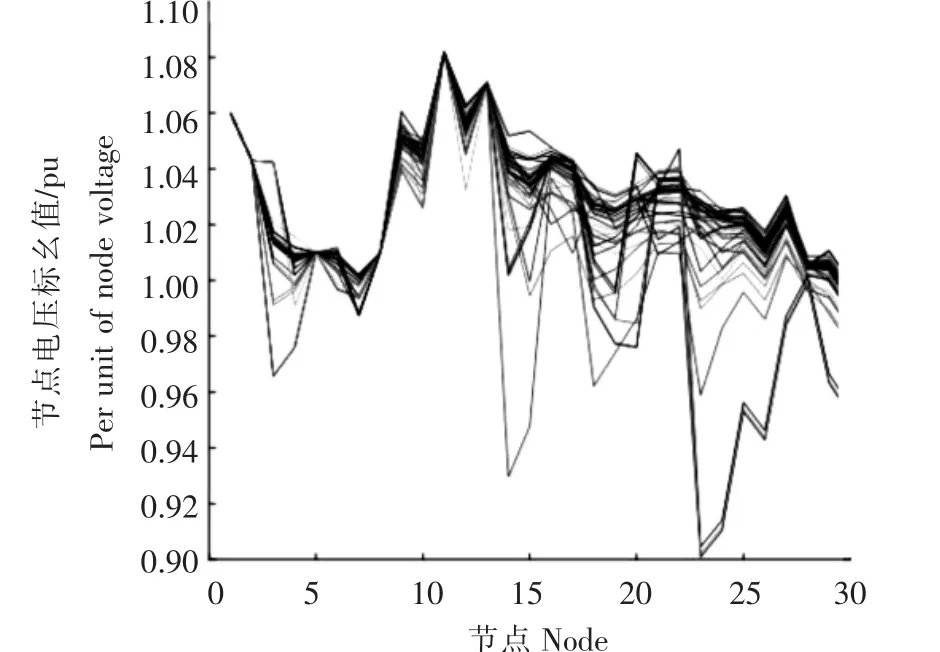
图13 考虑光伏输出和电网状态不确定性的各节点电压Figure 13 The node voltage under considering the uncertainty of photovoltaic output and grid state
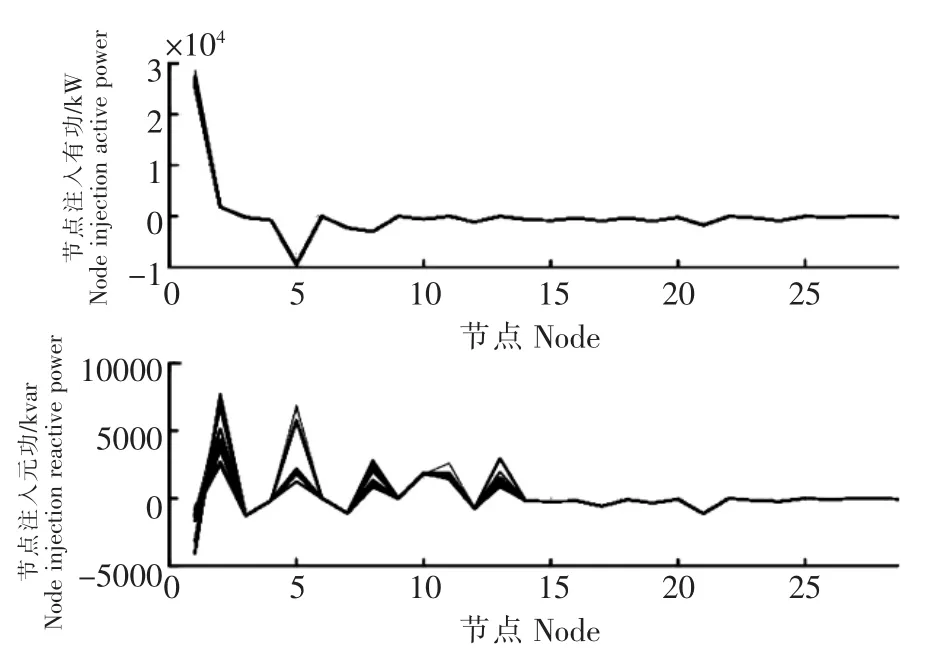
图14 节点注入功率的时序变化图Figure 14 Sequential variation of diagram of node injection power
4 讨论与结论
观察不同光伏出力对节点电压的影响,可发现光伏出力越大对节点电压影响越大,光伏接入可显著提高电网电压水平,改善电能质量。光伏的接入对不同节点有不同程度的影响,当接入点处于电网末端时对电网影响最大。若能合理的选择光伏的接入点及容量,必将能够有效改善电网电能质量。现阶段,在考虑系统不确定性的概率潮流研究中,均单独考虑可再生能源发电不确定性或电网状态不确定性,势必不能准确反映系统状态;另外,光伏发电功率具有时序的不确定性、波动性,所以针对电力系统的整体研究,也应对应考虑电网状态的时序不确定性,但在现有文献中鲜有讨论。相比光伏发电的周期性,电网线路的状态更加充满着不可控性,严重影响了电网的安全稳定运行,本研究采用的蒙特卡罗法在已知线路故障以及其修复时间的前提下,模拟出了72h内线路的状态,预测出了未来72h潮流分布情况。
本研究结果表明,通过学习逼近,建立了四输入一输出的BP神经网络光伏预测模型,成功预测了未来7d的光伏功率输出情况,将预测值与实际值相比较,计算均方差达到0.000256,可用于实际预测。另外,建立了考虑随机变量时序状态变化的光伏并网系统概率潮流计算方法。利用IEEE30标准算例验证了本研究提出方法的可行性和有效性,能够有效反映电网运行风险的电压、线路潮流,通过对潮流的分析,及时发现电网中存在的薄弱环节,有针对性地制定事故预防和电网改进措施。本研究验证了在电力系统潮流计算中综合考虑光伏接入和电网状态时序变化的必要性。
