THERMAL CREEP FLOW IN THE RAREFIED GAS∗

Feimin Huang

(Academy of Math.and System Sciences,CAS,Beijing 100190,PR China)

Abstract The usual heat flow moves along the direction from high temperature place to the low one,as often observed in the daily life.However,when the gas is very rarefied,the gas may move along a different way,that is,the so-called thermal creep flow moves along the direction from the low temperature place to the high one. In this note,we will survey our recent mathematical works on this topic,mainly based on[27]and[25].

Keywords thermal creep flow;rarefied gas;Boltzmann equation;low Mach limit;Compressible Navier-Stokes equations

1 Introduction

The usual heat flow moves along the direction from high temperature place to the low one,as often observed in the daily life. However,when the gas is very rarefied,an interesting phenomenon may happen. A so-called thermal creep flow moves along a different direction,that is,from the low temperature area to the high one,see the pictures below,

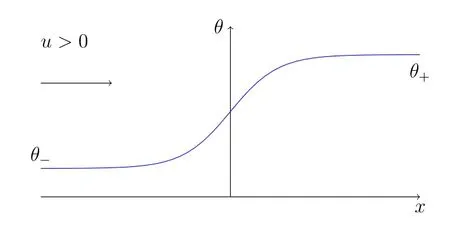
Figure 1:θ-＜ θ+

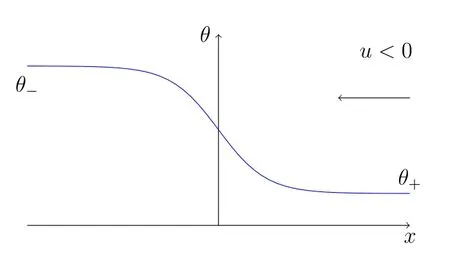
Figure 2:θ-＞θ+

whereθdenotes the temperature andudenotes the velocity of the flow.The thermal creep flow in a rarefied gas was known since the time of Maxwell.Since the funda-mental equation in statistical physics for rarefied gas is the Boltzmann equation,it is naturally conjectured that the Boltzmann equation provides more information in the microscopic level and can model the thermal creep flow. Although there have been a large of numerical computations on the basis of kinetic equation since 1960s,see[46-48]and the references therein,rigorous mathematical analysis is few.The first mathematial analysis was given in[10],later by[27].Recently the same phenomenon was also observed in the low Mach limit of compressible Navier-Stokes equations with non-trivial profile,see[25]. In the following two sections,we will survey the works on the thermal creep flow in both the Boltzmann equation[27]and the low Mach limit of the compressible Navier-Stokes equations[25].

2 Boltzmann Equation

The non-dimensional Boltzmann equation takes the form

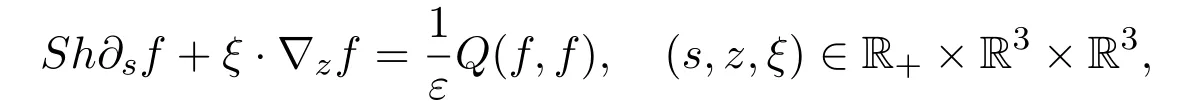
wheref(s,z,ξ)≥0 is the distribution function of particles,Q(f,f)is the collision operator with a kernel determined by the particle interaction.There are two parametersShandεcalled Strouhal and Knudsen numbers respectively. Their productSh·εistimes the ratio of the mean free time to the reference time.

There has been tremendous progress on the mathematical theories for the Boltzmann equation,see[4,5,7,12,14,15,17,26,28,29,36,37,51-53]and the references therein.Among them,the classical works of Hilbert,Chapman-Enskog revealed the close relation of the Boltzmann equation to the classical systems of fluid dynamics through asymptotic expansions whenSh=1 andεis small.

On the other hand,there are some phenomena described by the Boltzmann equation,for which the time evolution of the macroscopic components are not governed by the classical fluid dynamic systems. This happens,for example,when the parametersShandεas well as the macroscopic velocity are small while the density and temperature are of the order 1,such as the thermal creep flow phenomenon.There have been a lot of studies on this kind of phenomena which is called the“ghost effect”in the Boltzmann equation and most of the results are mainly built on the asymptotic expansions and numerical computations,see[5,46]and the references therein.A rigorous mathematical analysis for the ghost effect was first given in[10]where the thermal creep flow was studied for the stationary linearized Boltzmann equation. Recently we justified the thermal creep flow phenomenon for the Boltzmann equation[27],whose main results were outlined as follows.

We assume both the Strouhal number and the macroscopic velocity(that is,flow velocity)is of the order ofε,and rewrite the Boltzmann equation under the following scalings:

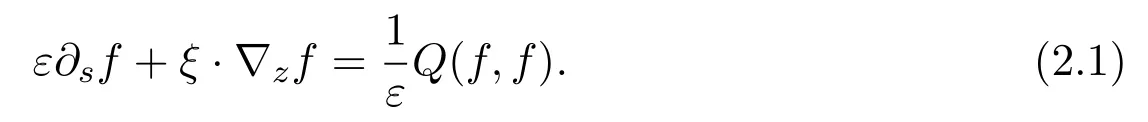
The solution to the Boltzmann equation has the following decomposition([5]):

whereM[ρ,εu,θ]is the local Maxwellian andGis the microscopic component. The local MaxwellianM[ρ,εu,θ]is defined by the five conserved quantities,that is,the mass densityρ(s,z),momentum densitym(s,z)=ερ(s,z)u(s,z)and energy densityE(s,z)+|εu(s,z)|2given by

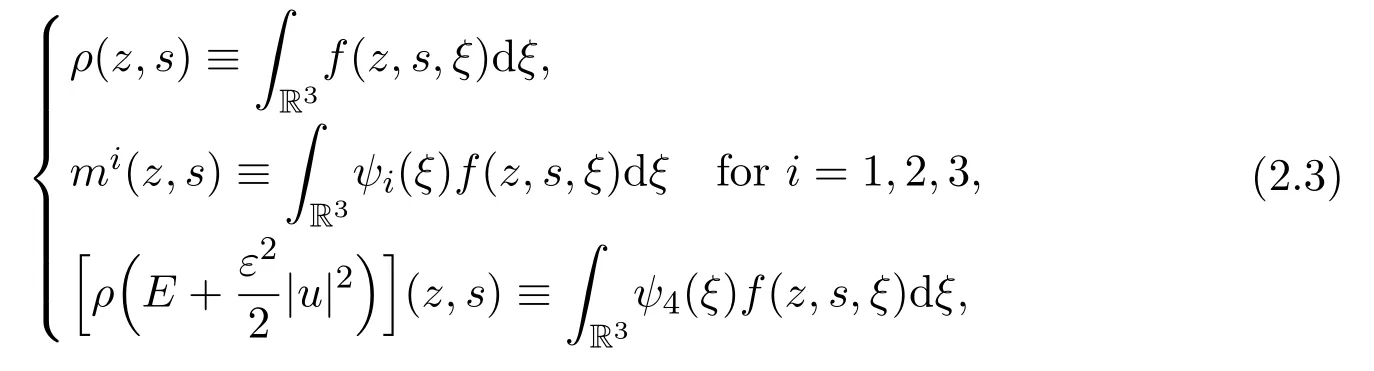
and

where the collision invariantsψα(ξ)are given by

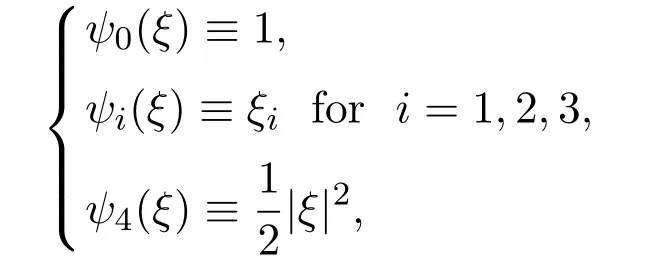
satisfying

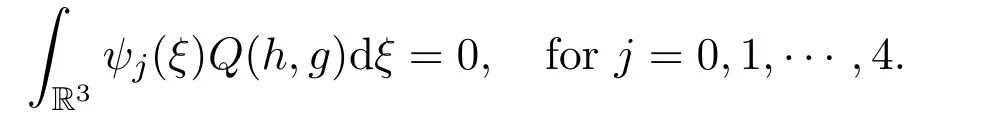
Hereθ(s,z)is the temperature related to the internal energyEbyE=RθwithRbeing the gas constant,andεu(s,z)is the flow velocity,uis the scaled flow velocity.

Whenεis small,an interesting phenomenon of the“ghost effect”is that the flow moves from the low temperature to the high one,while in the Euler or Navier-Stokes level,the flow moves from the high temperature to the low one,which is well known in heat flow. Therefore the resulted system of equations for these macroscopic variables,ρ,uandθare not given by either the classical Euler or Navier-Stokes equations. Indeed,by expanding the variables in the power ofεand by letting(ρ0,u0,θ0)be the leading order of the variables(ρ,u,θ),Bardos,Levermore,Ukai and Yang[5]derived the following system for(ρ0,u0,θ0)which is the same obtained by Sone using Hilbert expansion:

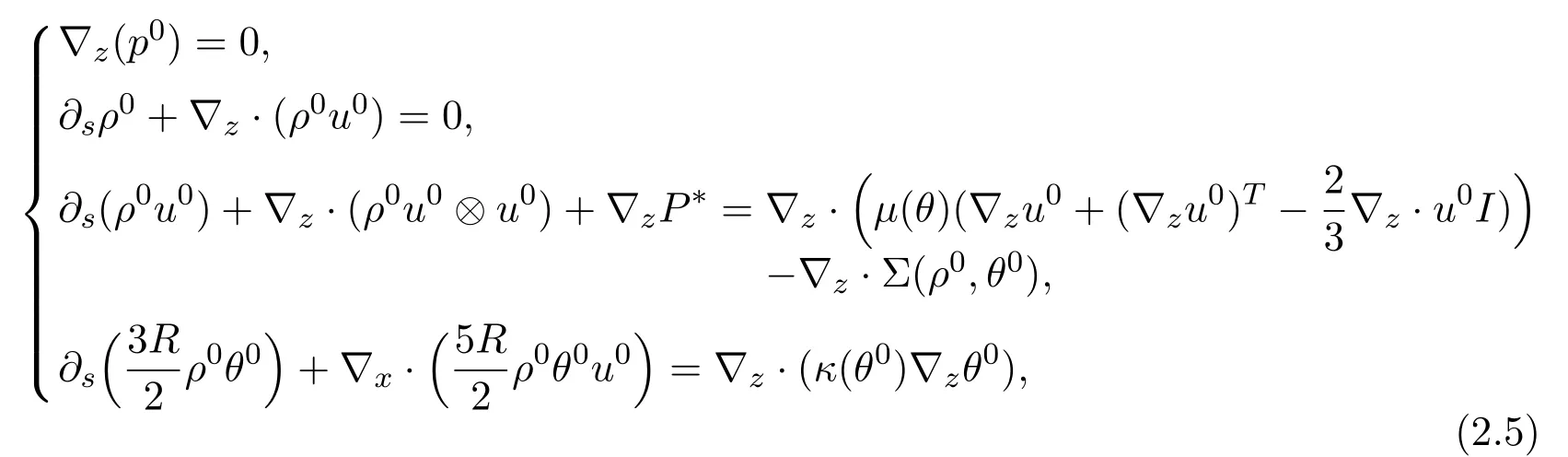
whereP ∗is an unknown scalar pressure while

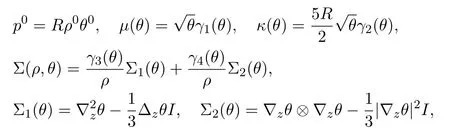
andIis the identity matrix andγj(θ)(j=1,2,3,4)are positive functions ofθ ＞0 whose explicit formulas can be found in the book by Sone[48]. Levermore,Sun and Trivisa[35]established the local well-posedness of the Cauchy problem of(2.5).We in[27]constructed a one dimension special solution of(2.5),which indeed can describe the thermal creep flow phenomenon,that is,the flow moves from the low temperature area to the high one,see Figures 1 and 2.The same phenomenon can also be observed in high dimension for system(2.5),see[24].Next we will show the 1-d special solution of the ghost effect system(2.5)for the thermal creep flow.

Note that system(2.5)in one space dimension reads

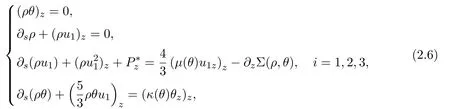
whereP ∗is an unknown function and

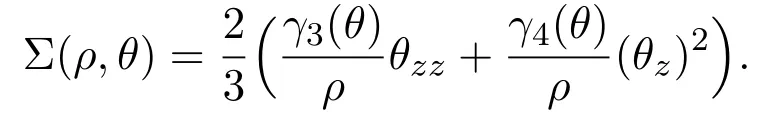
It is more convenient to rewrite the system and the equation by using theLagrangiancoordinates

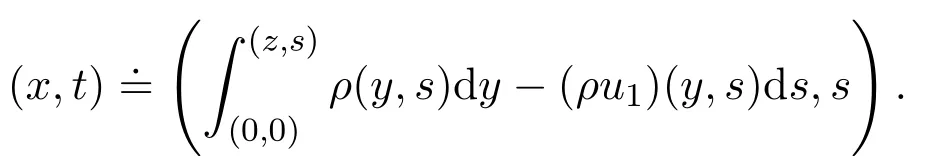
Then system(2.6)becomes

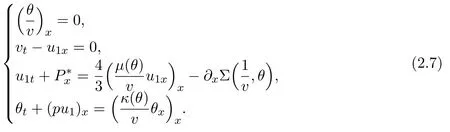
We normalize the gas constantRtobefor simplicity so thate=Rθ=θandp=Rρθ=ρθ.The viscosity coefficient µ(θ)＞0 and the heat conductivity coefficientκ(θ)＞0 are smooth functions of the temperatureθ.

From(2.7)1,we observe thatθ ≡vandp=,if we assume

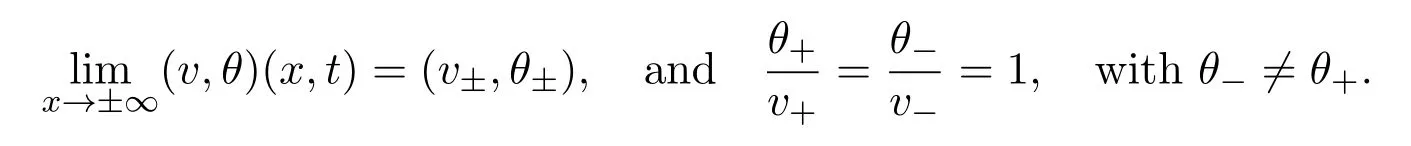
Then equations(2.7)4is rewritten as

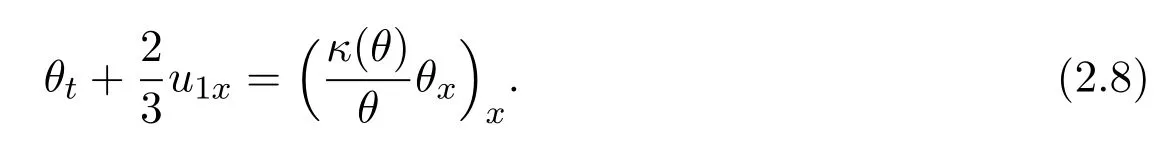
Substituting(2.7)2into(2.8)and noting thatv ≡ θ,we get the following scalar nonlinear diffusion equation

From[3]and[13],it is known that the nonlinear diffusion equation(2.9)admits a selfsimilar solution(η)withη=satisfying the boundary conditions(±∞,t)=θ±.Letδ=|θ+-θ-|,then(t,x)has the property that

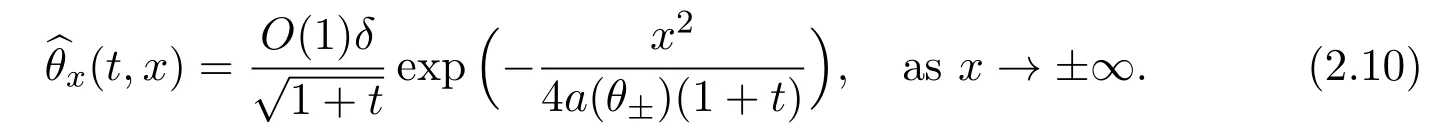
Define

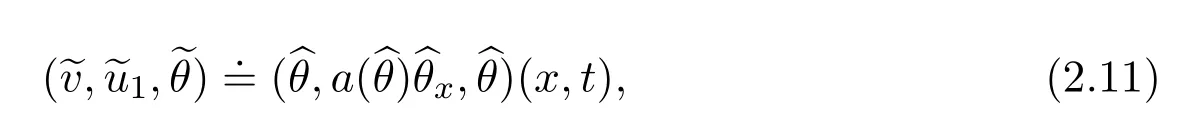
then from(2.9)it can be checked thatsatisfies system(2.7)as:

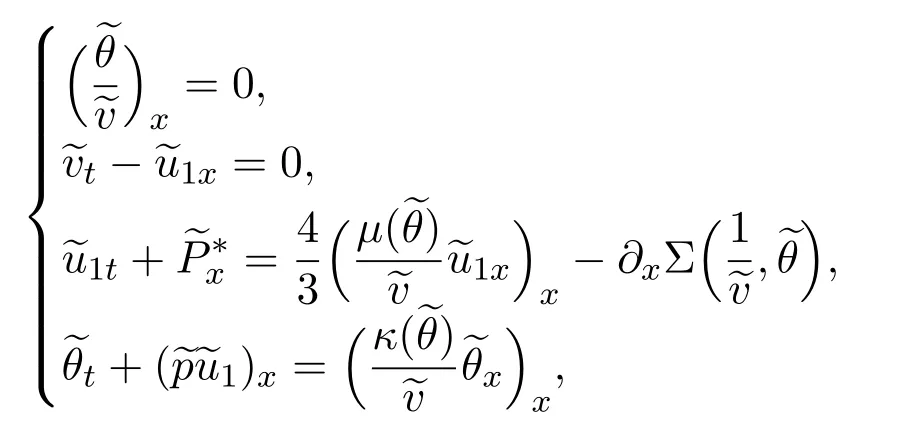
where

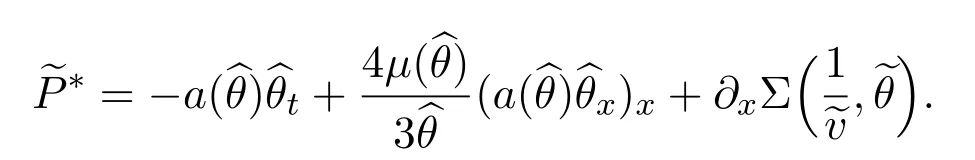
Remark 2.1Ifθ-＜ θ+,then＞0,that is,the flow moves from the low temperature to the high one,see Figure 1 in the previous section.The caseθ-＞ θ+also has the same phenomenon.These explicit solutions mean system(2.5)derived in[5]is indeed a good approximation for the ghost effect of the Boltzmann equation.

Remark 2.2The construction of the profileis motivated by the one of the viscous contact wave of compressible Navier-Stokes equations,see[23],[30]and[31].The viscous contact wave is used to approximate the contact discontinuity for compressible Euler equation and its pressure keeps constant.Thus we establish a relationship between the ghost effect for the Boltzmann equation and the viscous contact wave for the compressible Navier-Stokes equations.

Let's turn to the scaled Boltzmann equation with“slab symmetry”

For monatomic gas,the rotational invariance of the molecule leads to the collision operatorQ(f,f)as a bilinear collision operator in the form of,cf.[6]:

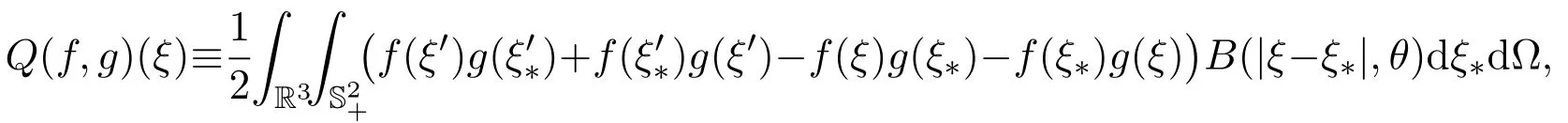
withθbeing the angle between the relative velocity and the unit vector Ω. Here={Ω∈S2: (ξ-ξ∗)·Ω≥0}.The conservation of momentum and energy gives the following relation between velocities before and after collision:

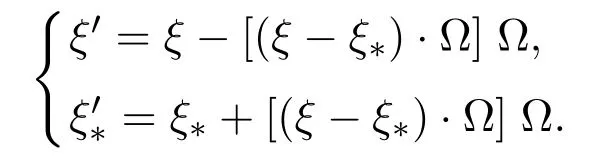
In this note,we will consider the Boltzmann equation for the hard sphere model,for simplicity,that is,the collision kernelB(|ξ-ξ∗|,θ)takes the forms

System(2.12)in the Lagrangian coordinates becomes

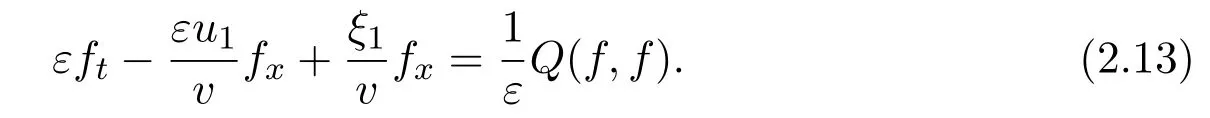
Based on the special solutionof the ghost effect system(2.7),we can construct a solution(v,u,θ,G)to the Boltzmann equation(2.13),which is a small perturbation ofsatisfying

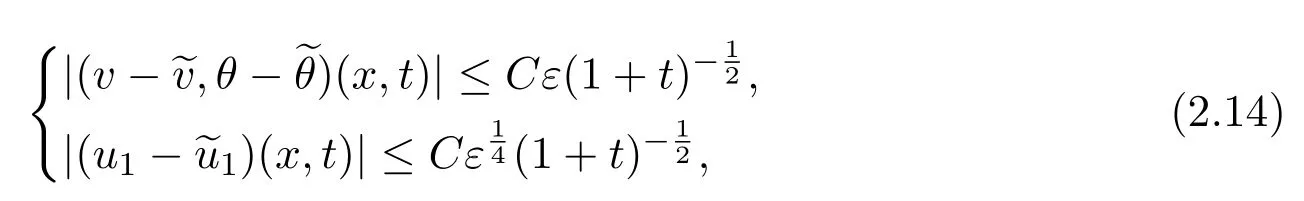
that is,the fluid part(v,u1,θ)of the solution of(2.12)converges to the solutionof(2.7)in the sense of(2.14)as the Knudsen numberεtends to zero,see[27]for details.Moreover,the flowis driven byas shown in Figures 1 and 2,therefore we justify the ghost effect expansion in the Knudsen number of the Boltzmann equation as for the thermal creep flow in a mathematical setting rigorously.

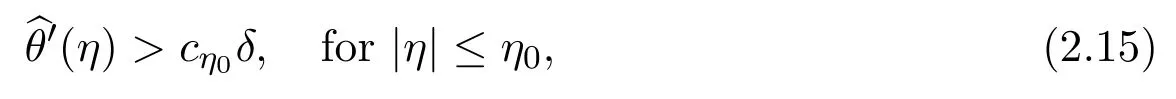
whereis a positive constant depending onη0.In[27],we further show that for any fixedη0＞0,there exists a small positive constantε1=ε1(η0)≤ ε0,such that ifε ≤ ε1,it holds that

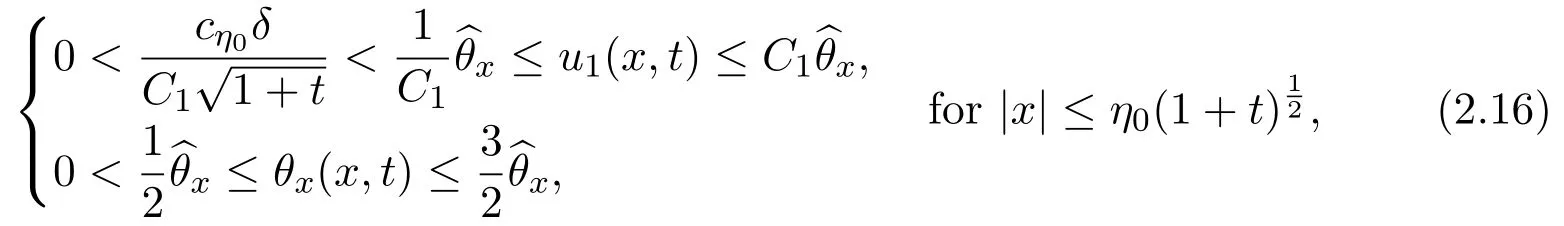
whereC1is a suitably large positive constant only depending onθ±.In particular,(2.16)implies that the flow is driven by the gradient of the temperature,that is,the flow speedu1is proportional to the temperature gradientθxin the sense of(2.16)on the region increasing with the time rate.

3 Low Mach Limit for Compressible Navier-Stokes Equations

Recently it was observed in[25]that the thermal creep flow phenomenon also happens in the low Mach limit for the non-isentropic Navier-Stokes system with non-trivial profile.Indeed,the N-S system in Rnreads

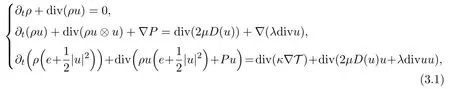
fort ＞0,x ∈Rn.Here the unknown functionsρ,u,andTrepresent the density,velocity,and temperature,respectively.The pressure function and internal function are defined by

where the parametersR ＞0 andcv ＞0 are respectively the gas constant and the heat capacity at constant volume.Here we renormalizeR=1 andcv=1.D(u)is the deformation tensor given by

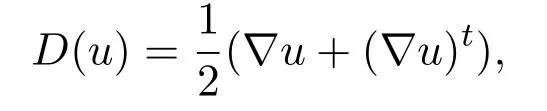
where(∇u)tdenote the transpose of matrix∇u.µandλare the Lam´e viscosity coefficients which satisfy

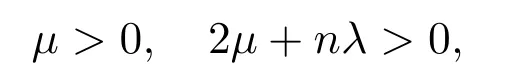
andκ ＞0 is the heat conductivity coefficient.For simplicity,we assume thatµ,λ,κare constants.

Letεbe the compressibility parameter which is a nondimensional quantity.As in[44],we set

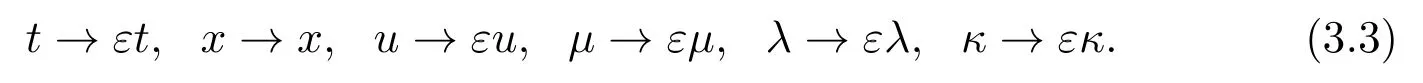
Based on the above changes of variables,the compressible Navier-Stokes system(3.1),written after the nondimensionalization,becomes

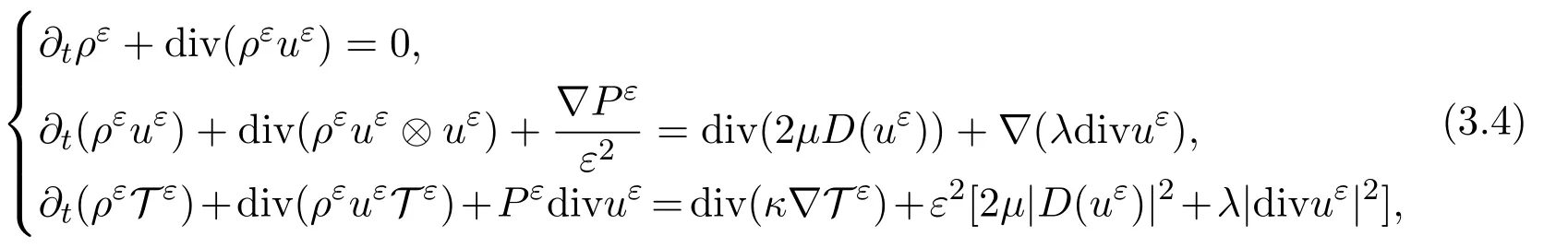
in which the typical mean fluid velocity has been chosen as the ratio of time units to space units.Accordingly,the parameterεessentially presents the maximum Mach number of the fluid.The limit of solutions of(3.4)asεgoes to 0 is usually called as low Mach limit[33,34].The purpose of the low Mach number approximation is to justify that the compression,due to pressure variations,can be neglected.This is a common assumption when discussing the fluid dynamics of highly subsonic flows.Similar to[1,44],we assume that the pressure is a small perturbation of a given constant state＞0,that is

Formally, as the Mach number tends to zero, system (3.4) becomes

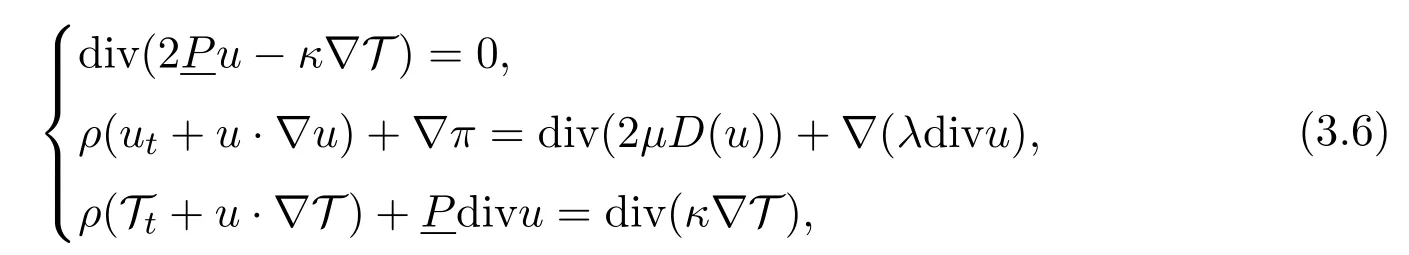
and the density satisfiesρ=/Tand

Without loss of generality,we normalizeto be 1. Let the approximate initial dataconverge to(pin,uin,Tin)asε →0 in some sense. Then,the approximate initial data is regarded as well-prepared data ifuinandTinsatisfies(3.6)1.Otherwise,it is called as ill-prepared data.

The low Mach limit is an important and interesting problem in the fluid dynamics. There have been a lot of literatures on the low Mach limit. The first result is due to Klainerman and Majda[33,34],in which they proved the incompressible limit of the isentropic Euler equations to the incompressible Euler equations for local smooth solutions with well-prepared data.Since then,there have been considerable progress in this topic,see([50],[2],[43],[41],[42],[1],[32],[11])and the references therein.

Note that in the whole space,all the above results require that both density and temperature have the constant background,that is

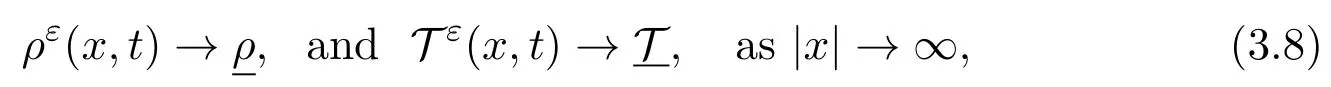
where＞0 and＞0 are given constants.In this note,we will show the low mach limit when the background is not a constant state in the one dimensional case,that is

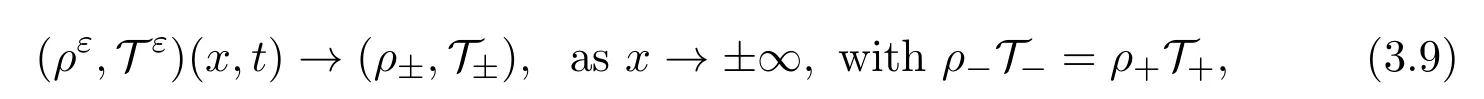
whereT-may not be equal toT+,and want to know what happens in the limiting process.In fact,we find the solutions of compressible Navier-Stokes equations converge to a nonlinear diffusion wave solution globally in time as Mach number goes to zero.In particular,the velocity of diffusion wave is only driven by the variation of temperature.This phenomenon looks like thermal creep flow[20,27,45].Moreover,when Mach number is small,the compressible Navier-Stokes system also has the same property,which has never been observed before.

Now let's formulate the main results.System(3.4)and the limiting system(3.6)in one dimension become,respectively,

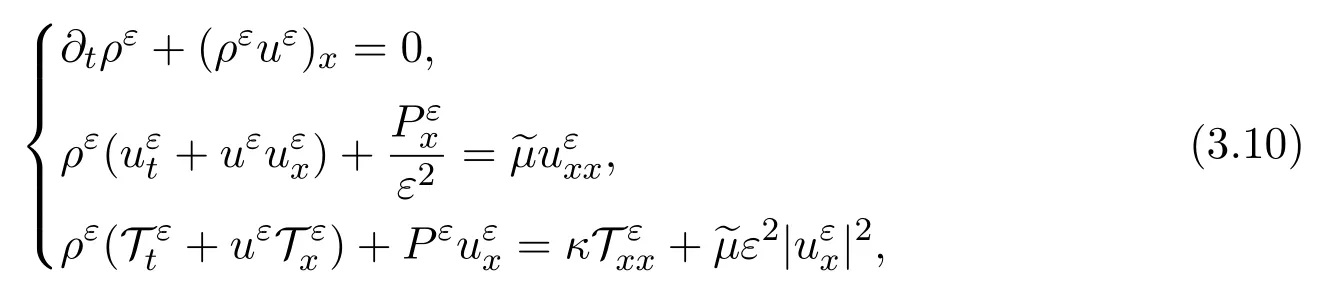
and

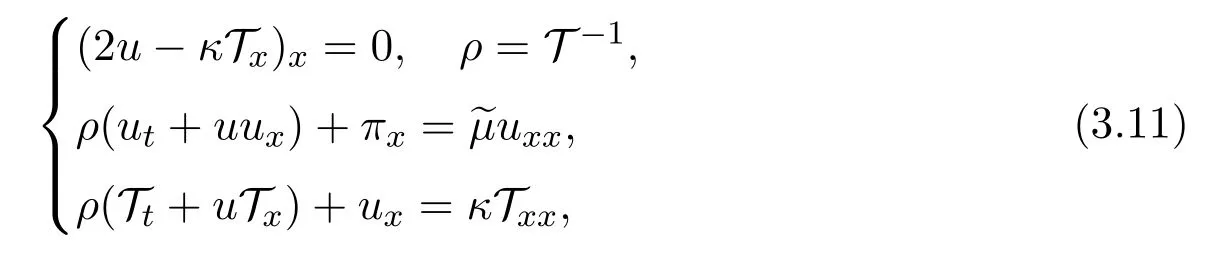
where(x,t)∈R×R+and~µ=2µ+λ ＞0.We shall construct a special solution of(3.11).Indeed,from(3.11)1,we choose

Substituting(3.12)into(3.11),as in previous section for the ghost effect system(2.7),we again obtain a nonlinear diffusion equation

From[3]and[13],it is known that the nonlinear diffusion equation(3.13)admits a unique self-similar solution Ξ(η),η=satisfying Ξ(±∞,t)=ρ±.Letδ=|ρ+-ρ-|,then Ξ(t,x)satisfies

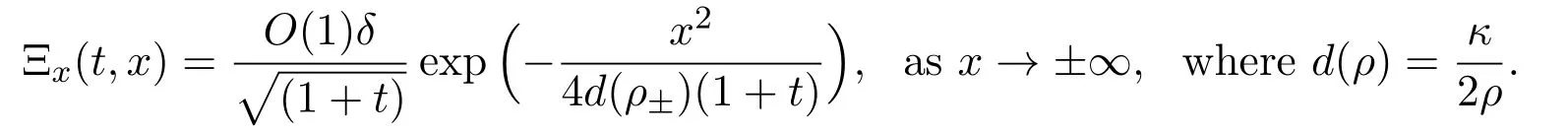
We define

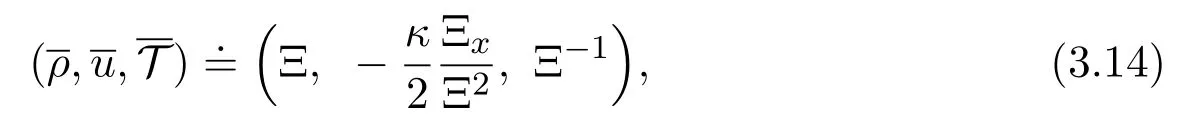
which is a special solution of(3.11),that is

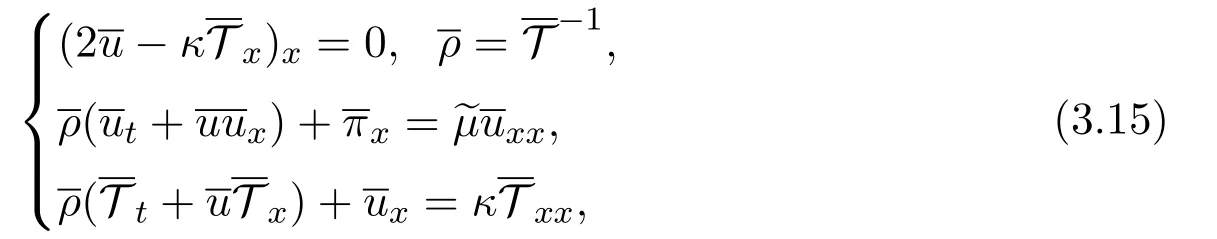
Figure 3

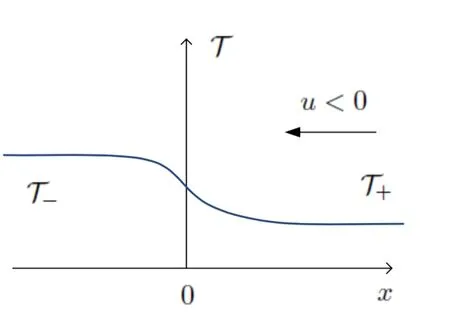
Figure 4

It should be noted that the usual Poiseuille flow moves from the high pressure part to the low one due to the difference of pressure.

3.1 Main Results

As in the previous section,it is more convenient to use theLagrangiancoordinates for the global behavior of solutions.That is,take the coordinate transformation

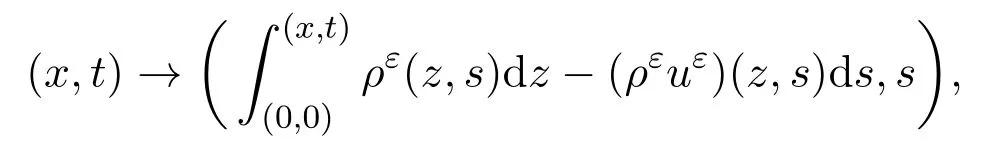
which is still denoted as(x,t)without confusion.Letv=be the specific volume.Then,in the Lagrangian coordinates,system(3.10)becomes

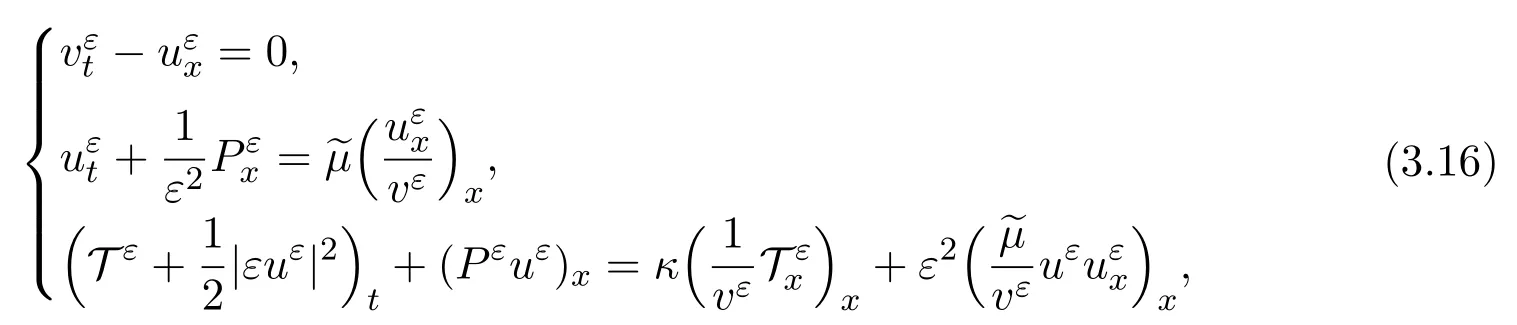
where the pressureP=v-1T. Similarly,the limiting system(3.15)in the Lagrangian coordinate becomes

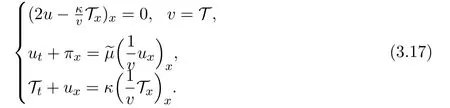
As in(3.14),we can construct a special diffusive wave solutionof(3.17)by choosing

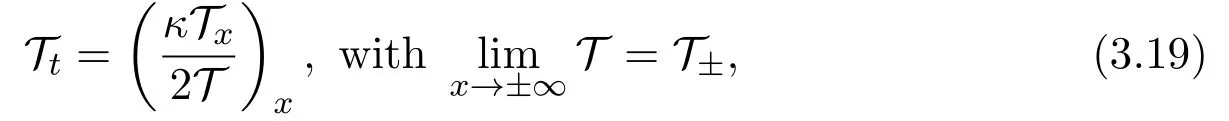
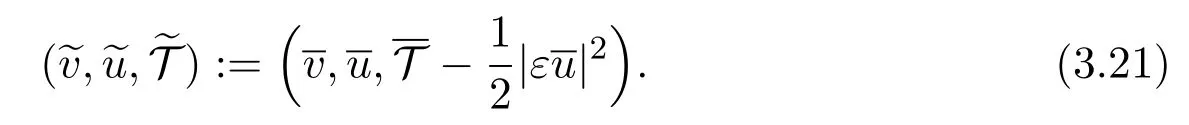
A direct calculation gives that

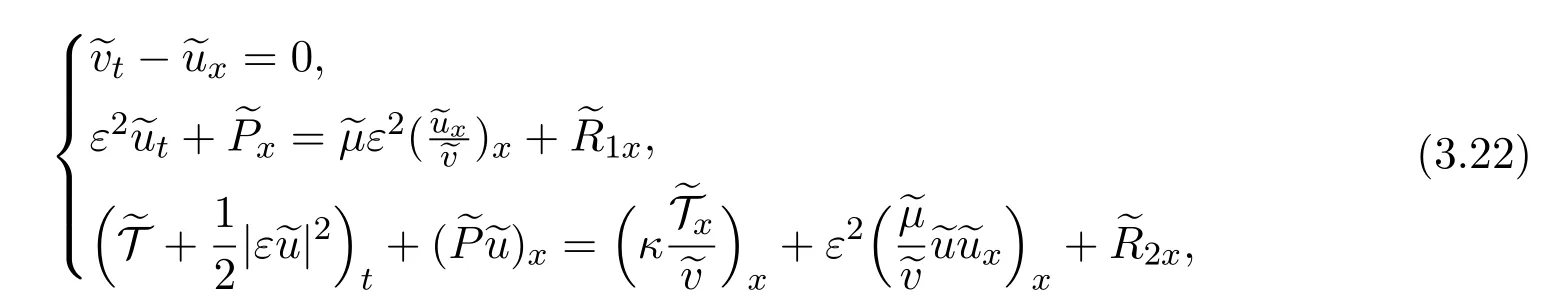
where

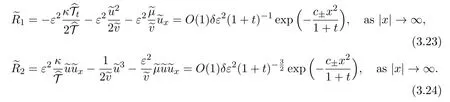
It follows from(3.18)and(3.21)that

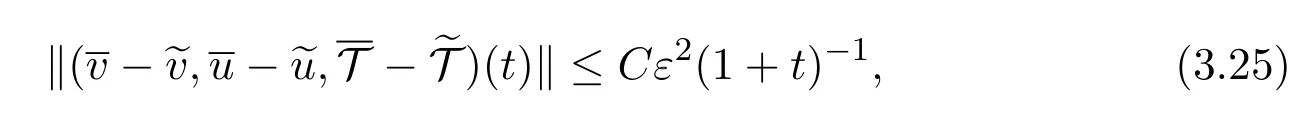
We consider system(3.16)with the initial data

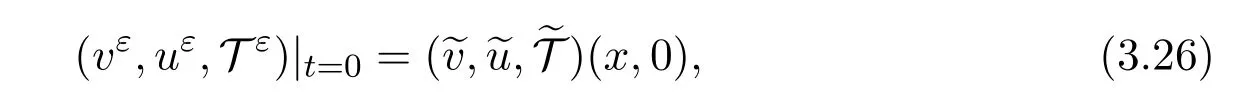
then the following global existence and uniform estimates hold.

Theorem 3.1(Uniform Estimates[25])Let(~v,~u,~T)(x,t)be the diffusive wave defined in(3.21)with the wave strength δ=|T+-T-|.There exist positive constants δ0and ε0,such that if δ ≤ δ0and ε ≤ ε0,then the Cauchy problem(3.16),(3.26)has a unique global smooth solution(vε,uε,T ε)satisfying

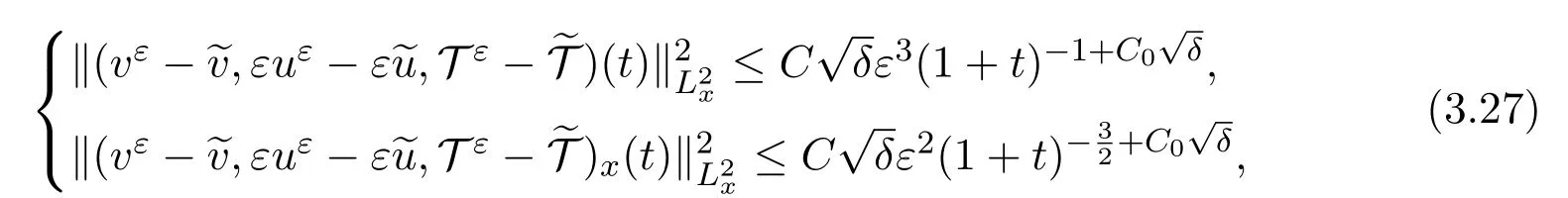
where C and C0are positive constants independent of ε and δ.

Based on the uniform estimates(3.27)and Sobolev embedding,we can justify the following low Mach limit.

Corollary 3.1(Low Mach Limit[25])Under the assumptions of Theorem3.1,it follows from(3.25)and(3.27)that as ε →0,

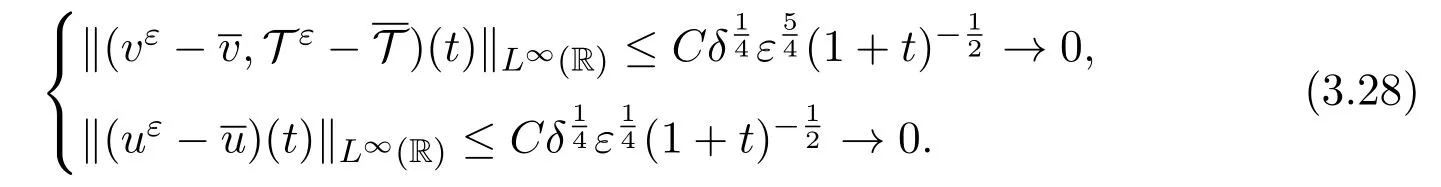
Moreover,we have:

Corollary 3.2(Driven by the Variation of Temperature[25])For the solutions obtained in Theorem3.1,there exists a small positive constant ε1=ε1(η0)≤ ε0,such that if ε ≤ ε1,it follows from(3.28)and(3.29)that

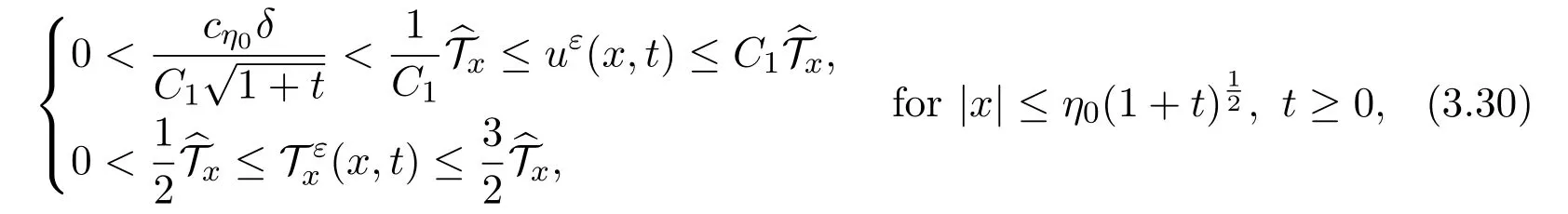
which yields immediately that

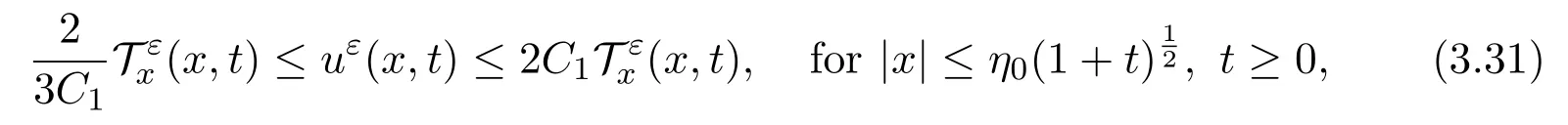
where C1is a suitably large positive constant depending only on T±.

Remark 3.1The estimate(3.31)shows that the velocityuεof the compressible Navier-Stokes system(3.16)is also driven by the variation of temperature whenεis small.Note that the pressurePis almost 1,this phenomenon behaviors like thermal creep flow[20,27,45].

Remark 3.2Note that the diffusion wave defined in(3.19)is independent of the viscosityµ,this hints that the thermal creep flow can be also observed in the low Mach limit for the non-viscous and heat-conductive gas,that is,µ=0. This was investigated in[39].