MULTIPLE VORTICES FOR THE SHALLOW WATER EQUATION IN TWO DIMENSIONS∗†
2019-12-25DaominCao
Daomin Cao
(Institute of Applied Math.,Chinese Academy of Science,Beijing 100190,PR China)
Zhongyuan Liu
(School of Mathematics and Statistics,Henan University,Kaifeng 475004,Henan,PR China)
Abstract In this paper,we construct stationary classical solutions of the shallow water equation with vanishing Froude number Fr in the so-called lake model.To this end we need to study solutions to the following semilinear elliptic problem for small ε >0,where p >1,div =0 and Ω ⊂R2 is a smooth bounded domain.
Keywords shallow water equation;free boundary;stream function;vortex solution
1 Introduction and Main Results
In this paper,we consider fluid contained in a basin by a uniform gravitational acceleration g and fixed vertical lateral boundaries(that is,no sloping beaches).Suppose that(x,y)is horizontal spatial coordinate which is confined to a fixed bounded domain Ω with boundary∂Ω.The vertical coordinate is chosen so that the mean height of the fluid's free upper surface is atz=0.Letz=-b(x,y)give the fixed bottom topography,sobis a strict positive function over Ω.Letz=h(x,y)be the free upper surface.We assume that bothband∂Ω vary over distancesLwhich are large compared to typical depthB,that is,the ratiois small.
Let u andwdenote the horizontal and vertical components respectively of the fluid velocity. We will consider only those motion for which u,wandheach vary in(x,y)over distancesL,in other words,we will make the long-wave approximation.The“Froude number”is denoted as,whereUis the characteristic magnitude of u.We will consider the case of small“Froude number”Frandhis small compared toB.In such cases,from[1,3,4,19],the leading-order evolution of u(x,y,t)andh(x,y,t)will be governed by equations that have the non-dimensional form
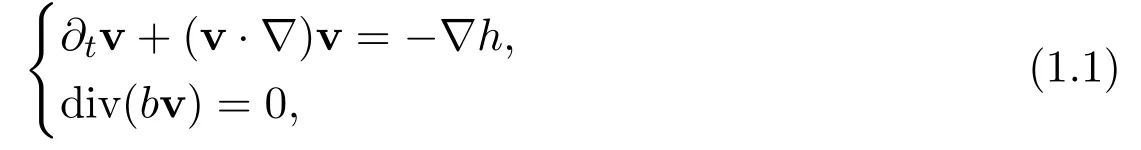
where ∇is the horizontal gradient.Since these equations are applied to a domain which is shallow compared to its width and whose free surface exhibits negligible surface motion,they are called the“lake”equations(see[4],for instance).
The first equation in(1.1)can be rewritten in terms of the vorticityω=∇×v:=as
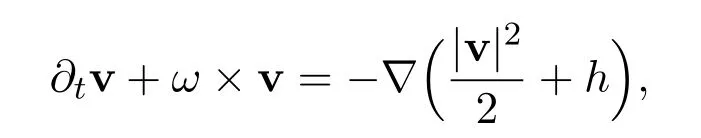
ω×v=(-v2ω,v1ω).This model is analogous to the two-dimensional Euler equation for an idea incompressible fluid and has been recently studied by many authors.For instance,see[1,3,4,19]and the references therein.
Recently,De Valeriola and Van Schaftingen[9]studied the desingularization of vortices for(1.1)with the stream function method,which consists in observing that ifψsatisfies
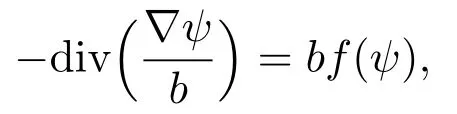
forf∈C1(R),then v=,andh=-F(ψ)-withF(s)=f(s)dsform a stationary solution to the shallow water equation. Moreover,the velocity v is irrotational on the set wheref(ψ)=0. It is easy to see that ifψ0satisfies-div=0,then v0=,h0=-is an irrotaional stationary solution to(1.1).In[9],they studied the asymptotics of solutions to
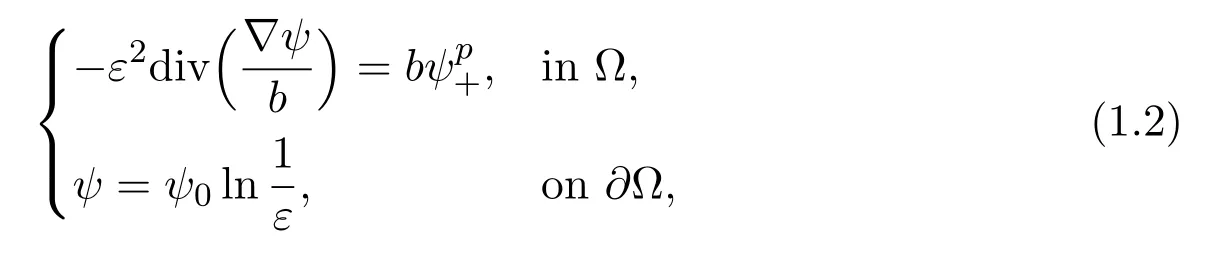
wherep >1,Ω ⊂R2is a smooth bounded domain.
Letψ=u-qln,whereq=-ψ0,then(1.2)becomes
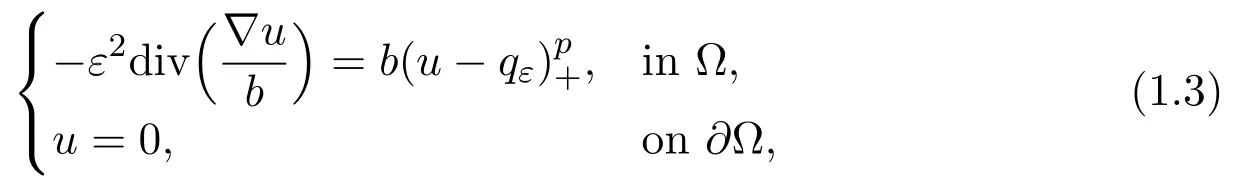
wherep >1,qε=qln,Ω ⊂R2is a smooth bounded domain.
More precisely,they first obtained the existence of solutions to(1.3)by using mountain pass lemma and studied the asymptotic behavior of solutions by giving exact estimates to the upper and lower energy bounds of the least energy solutions.As a consequence,they obtained that the“vortex core”shrinks to a pointx0which is the minimum point of.However,it is hard to apply their method to construct multiple vortices for(1.1).Moreover,they also considered desingularization of vortex ring for three dimensional axisymmetric incompressible Euler equations. We will construct multiple vortex rings in the future work.
Motivated by[9],our goal in this paper is to construct multiple stationary vortices for shallow water equations. More specifically,we want to find some high energy solutions whose“vortex core”consists of multiple components which shrink to several distinct points inasε→0 under some additional assumptions on.
Our main results in this paper can be stated as follows:
Theorem 1.1Suppose thatΩ ⊂R2is a smooth(boun)ded domain.Suppose thatb∈C2(),>0and=0.Then,for any givenψ0<0satisfying-div
strictly local minimum(maximum)points,···,of,there exists an ε0>0,such that for each ε∈(0,ε0),there exists a family of solutionsvε∈C1(Ω,R2)and hε∈C1(Ω)of
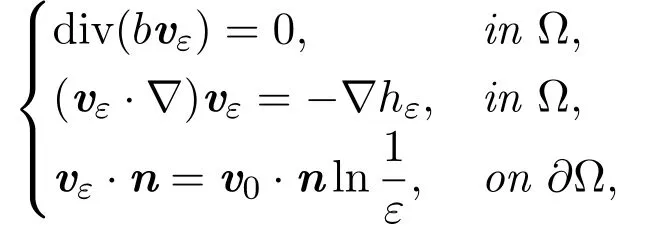
such that its vorticity ωε:=curl vεsatisfying
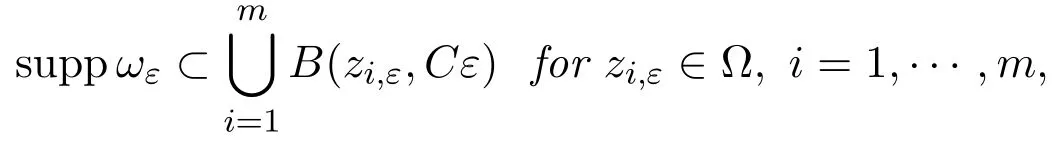
and as ε→0,
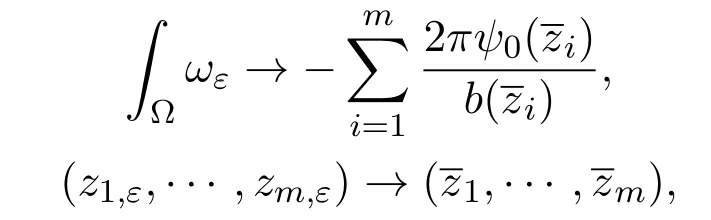
wherenis the unit outward normal of ∂Ω,C is a positive constant.
Remark 1.1Sincezi,ε→asε→0,we have
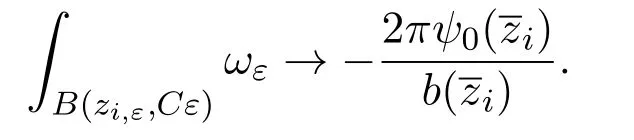
Thus,as in[9],we can obtain from(i=1,···,m)that
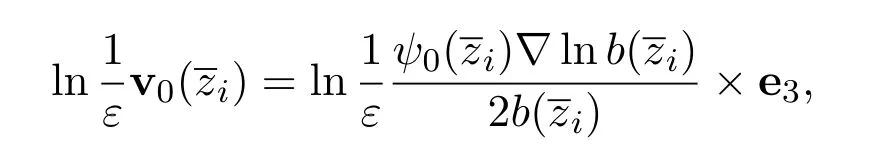
which is consistent with Richardson's asymptotics as in[9,19].
The next result shows that strictly local minimum points ofon the boundary∂Ω can also lead to vortex solutions to(1.1).
Theorem 1.2Suppose thatΩ ⊂R2is a smooth bounded domain. Supposethat b∈C2(),>0and<0satisfying-div=0. Then,forany given strictly local minimum points,···,ofon the boundary ∂Ω,thereexists an ε0>0,such that for each ε∈(0,ε0),there exists a family of solutionsvε∈C1(Ω,R2)and hε∈C1(Ω)of
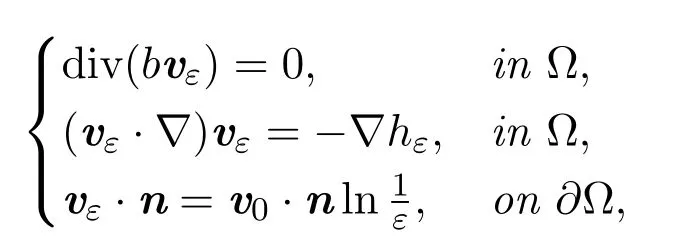
such that its vorticity ωε:=curl vεsatisfying
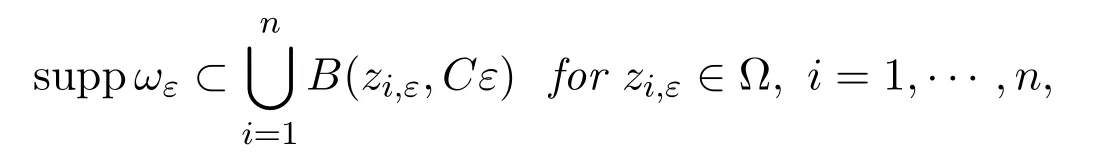
and as ε→0,
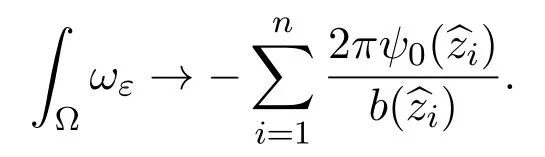
Moreover,
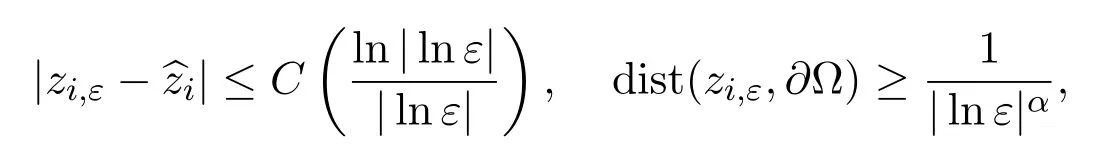
wherenis the unit outward normal of ∂Ω,α,C are positive constants.
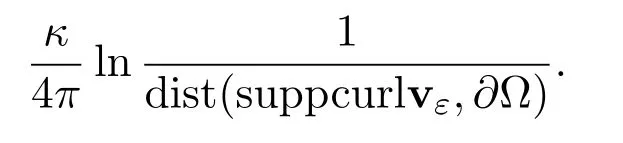
Hence,the Richardson's asymptotics does not hold in this case.There is a similar situation for the two dimensional Euler equation as in[20].Ifbis a constant,thenbhas no impact on the location of vortex. This case has been studied by some authors,see references[15,16,20]for more details.
Remark 1.2Ifhas strictly local minimum points in Ω and on the boundary∂Ω,there is,from Theorems 1.1 and 1.2,a stationary solution to the shallow water equation such that its vorticity set shrinks to the corresponding strictly local minimum points.Moreover,ifψ0is a nonzero constant,then we can obtain the existence of stationary solutions satisfyingvε·n=0 on∂Ω.
It is worthwhile to pointing out that although the structure of shallow water equations is very analogous to that of two dimensional Euler equations for an ideal incompressible fluid,the position of vortex for(1.1)exhibits a striking difference with that of the Euler equations.The position of vortex for Euler equation is closely related to Kirchhoff-Routh function.The interested reader can refer to[5,8,17,18,20]for more results on this problem.
Theorems 1.1 and 1.2 are proved via the following results concerning problem(1.3).
Theorem 1.3Suppose thatΩ ⊂R2is a smooth bounded domain.Suppose thatb,q∈C2(),>0and>0. Then,for any given strictly local minimum(maximum)points,···,of,there exists an ε0>0,such that for eachε∈(0,ε0),(1.3)has a solution uε,such that the setΩε={x:uε-qln>0}has exactly m componentsΩε,i,i=1,···,m and as ε→0,eachΩε,ishrinks to thepoint.
Theorem 1.4Suppose thatΩ ⊂R2is a smooth bounded domain. Let b,q∈C2(),>0and>0.Then,for any given strictly local minimum points,···,ofon the boundary ∂Ω,there exists an ε0>0,such that for eachε∈(0,ε0),(1.3)has a solution uε,and the setΩε={x:uε-qln>0}has exactlym componentsΩε,i,i=1,···,m and as ε→0,eachΩε,ishrinks to the point.
To obtain good estimates for approximate solutions and to simplify notations,unlike in[9]we do not investigate(1.3). Instead we change(1.3)to the following equivalent problem.then(1.3)becomes
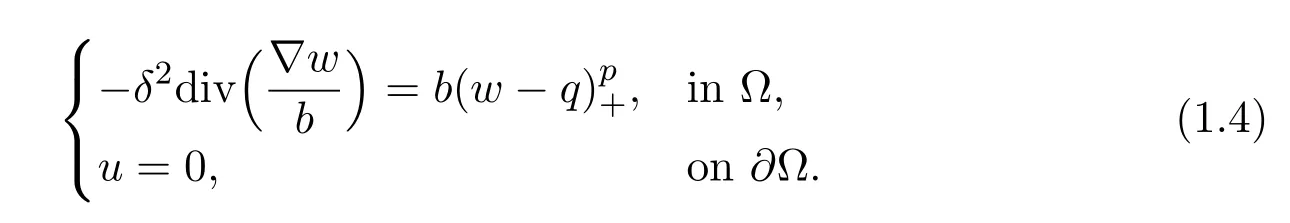
Let us outline the proof of the main results of this paper.The solutions in[9]were obtained by finding the least energy solutions to the corresponding function-al in a suitable function space. This method is hard to construct solutions whose vorticity set has several components.In the present paper,we will use a reduction argument to prove Theorems 1.3 and 1.4. To this end,we need to construct an approximate solution to(1.4). For the problem studied in this paper,the corresponding“limit”problem in R2has no bounded nontrivial solution. So,we will follow the method in[7,10]to construct an approximate solution.Since there are two parametersδ=ε(|lnε|)andbin problem(1.4),which causes some difficulty,we must take this influence into careful consideration and give delicate estimates in order to perform the reduction argument. In addition,to get better estimates for approximate solutions,we need to choose the parameters suitably,for example,=1,···,min Section 2.We will also apply the above idea and techniques to construct vortex pairs to shallow water equations in Section 5,which has never been addressed before.Fraenkel[11]constructed vortex rings for an unbounded inviscid fluid with uniform density.The novel idea is to consider an equivalent integral equation and then split it into linear and nonlinear components.The reduction method is basically the same as the argument of Fraenkel.However,our methods give more finer estimates of vortices.
As a final remark,our results seem connected with the work of Wei,Ye and Zhou[21,22]on the anisotropic Emden-Fowler equation
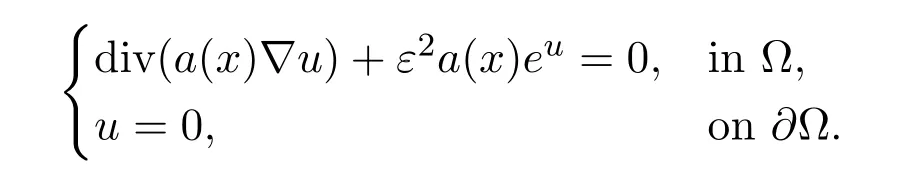
They constructed(boundary)bubbling solutions showing a striking difference with the isotropic case(a≡constant). Moreover,we point out that problem(1.4)can be considered as a free boundary problem. Similar problems have been studied extensively. The reader can refer to[5-7,9,10,13,16,20]for more results on this kind of problems.
This paper is organized as follows.In Section 2,we construct the approximate solution to(1.4). We will carry out a reduction argument in Section 3 and prove the main results in Section 4.In Section 5,we give some further results on vortex pairs for the shallow water equations.Some basic estimates used in Sections 4 and 5 will be given in Section 6.
2 Approximate Solutions
In this section,we will construct approximate solutions to(1.4).
LetR >0 be a large constant,such that for anyx∈ Ω,Ω ⊂⊂BR(x).For any givena >0,it is well-known from[10]that the following problem

has a unique positive solutionWδ,a,which can be written as

whereφ(x)=φ(|x|)is the unique solution to
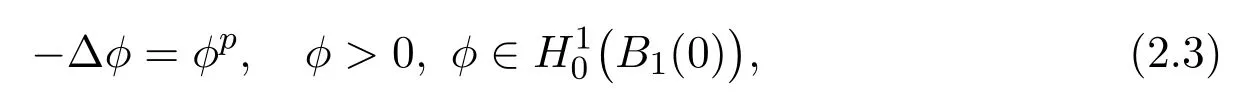
andsδ∈(0,R)is determined by
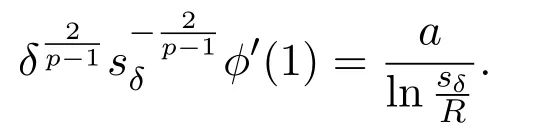
Thus it is easy to check(see[10])that
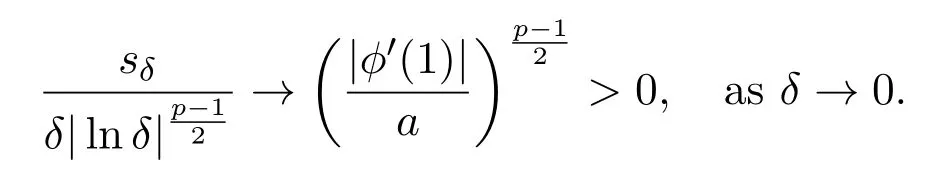
Moreover,by Pohozaev identity(see Lemma 4.3 in[16]),we have
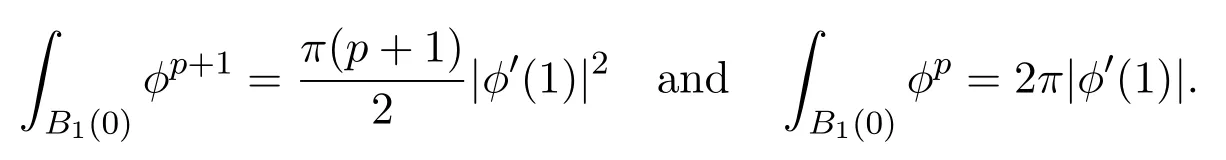
We now consider the following problem

Taking advantage of(2.1)and(2.2),we obtain
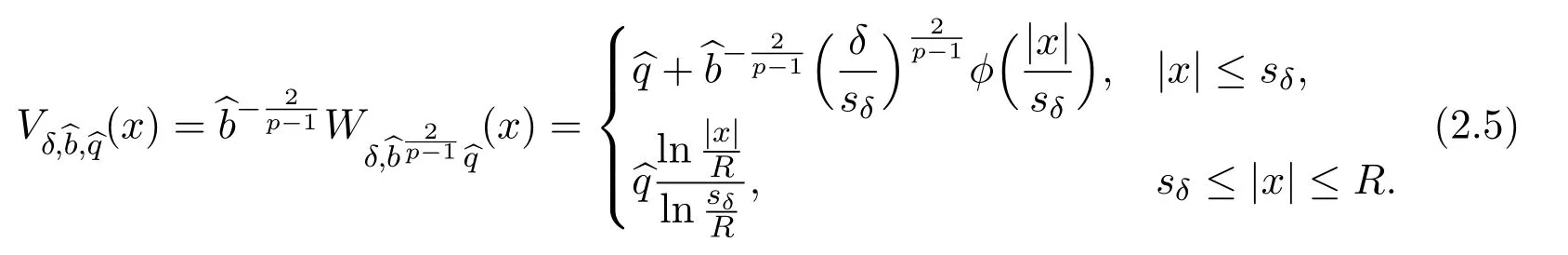
For anyz∈ Ω,define(x)=(x-z).BecauseVδ,^b,^qdoes not vanish on∂Ω,we need to make a projection.Letbe a solution to
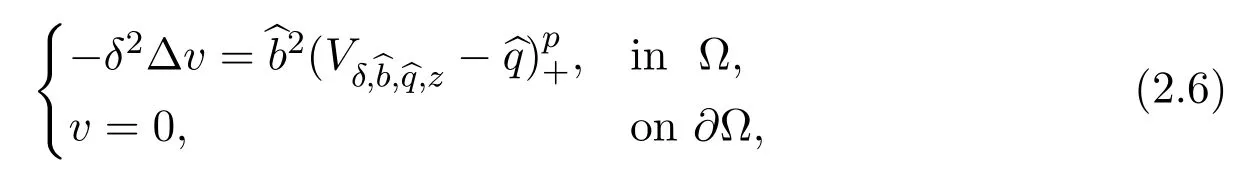
andh(x,z)be the regular part of the Green function with Dirichlet boundary condition(see[5,16,20]),that is the solution to
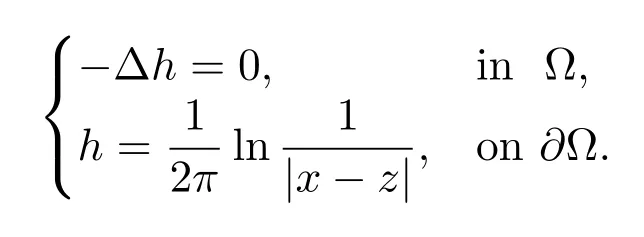
Then
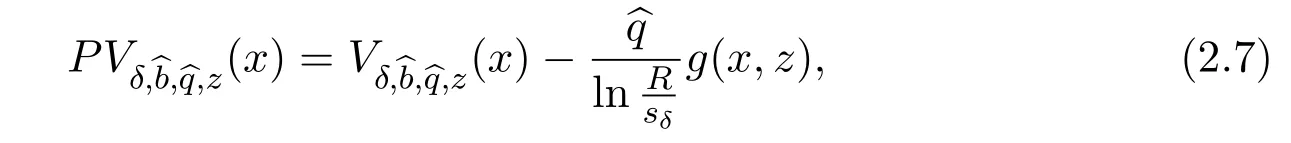
whereg(x,z)=lnR+2πh(x,z).
We will construct solutions to(1.4)of the form
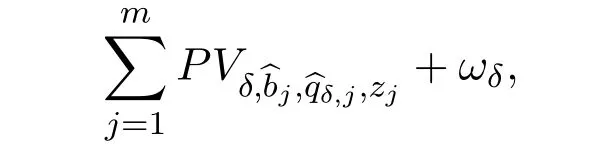
wherezj∈ Ω forj=1,···,m,ωδis a perturbation term.To makeωδas small as possible,we need to chooseproperly.
DenoteZ=(z1,···,zm)∈R2m.In this paper,we always assume thatzj∈ Ωsatisfies
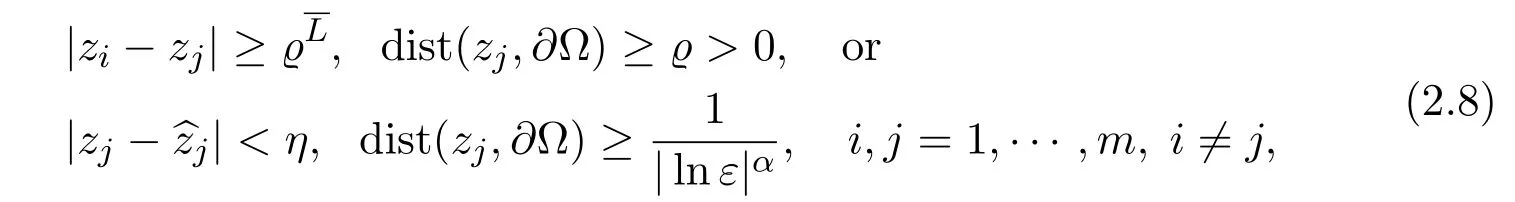
whereϱ,η >0 is a fixed small constant andα >0 are fixed large constants.
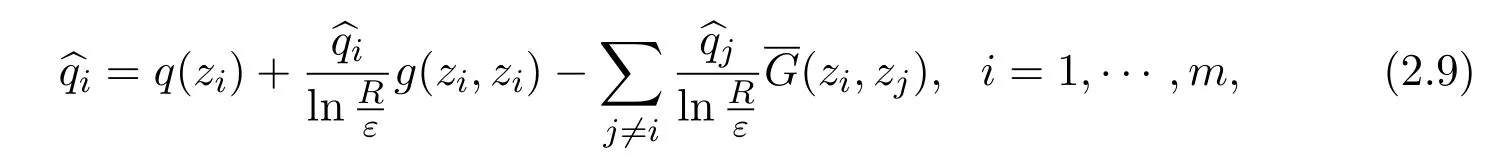
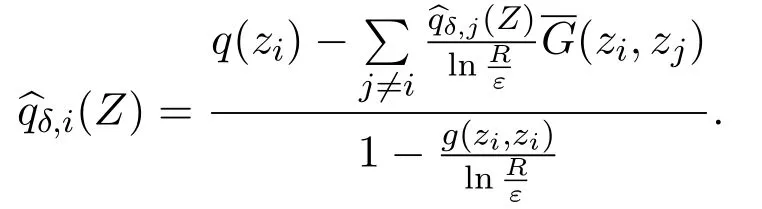
For simplicity,for givenZ=(z1,···,zm),in this paper,we will useto denoteq^δ,i(Z).Define
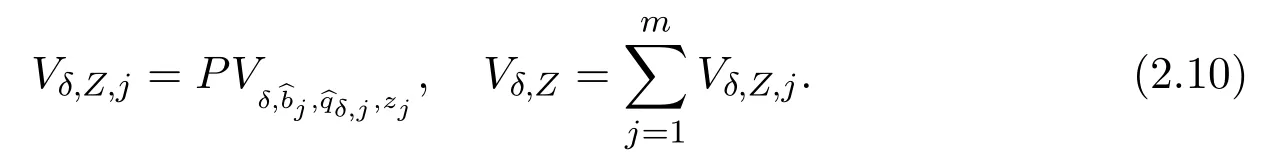
Setsδ,ito be the solution to
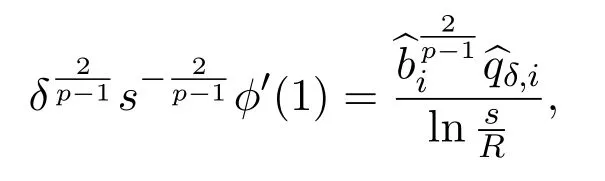
then,from[10,16],we have

Thus,we find that forx∈BLsδ,i(zi),whereL >0 is any fixed constant,
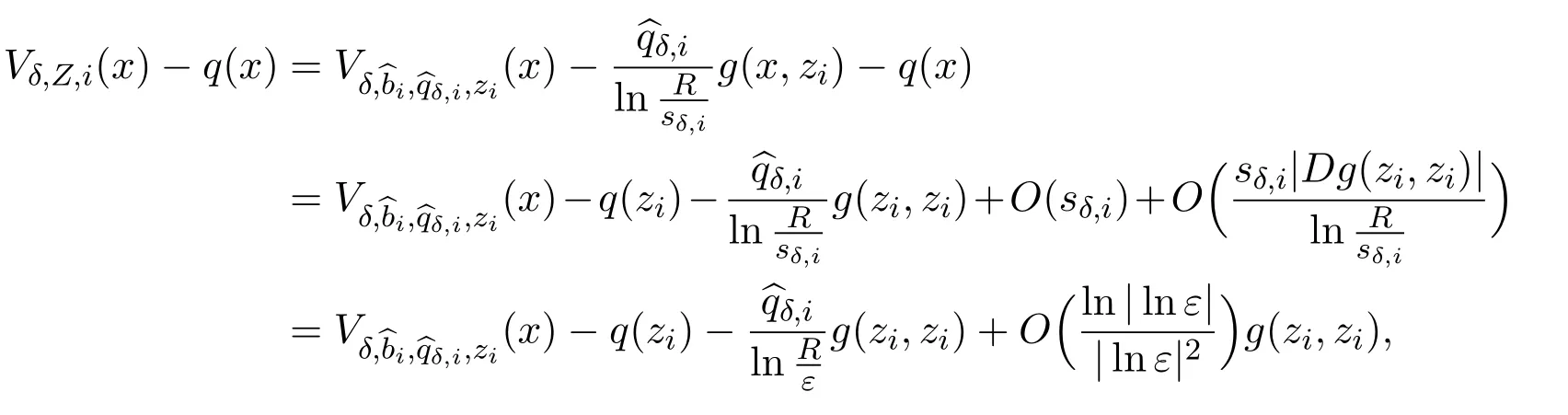
and forj̸=iandx∈BLsδ,i(zi),
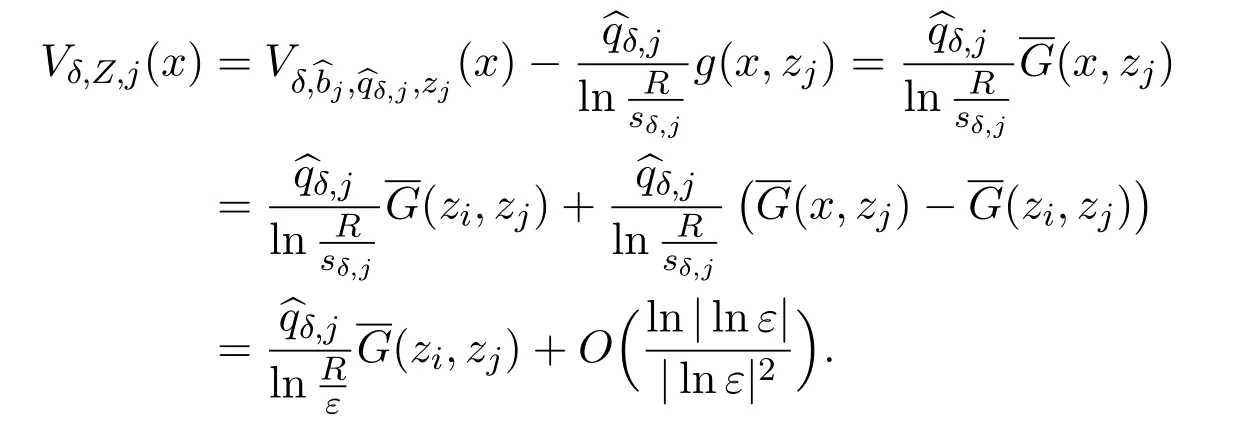
So,by using(2.9),we obtain
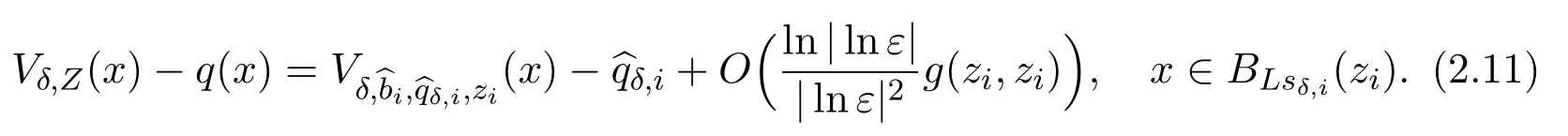
We end this section by giving the following formula which can be obtained by direct computation and will be used in the next two sections
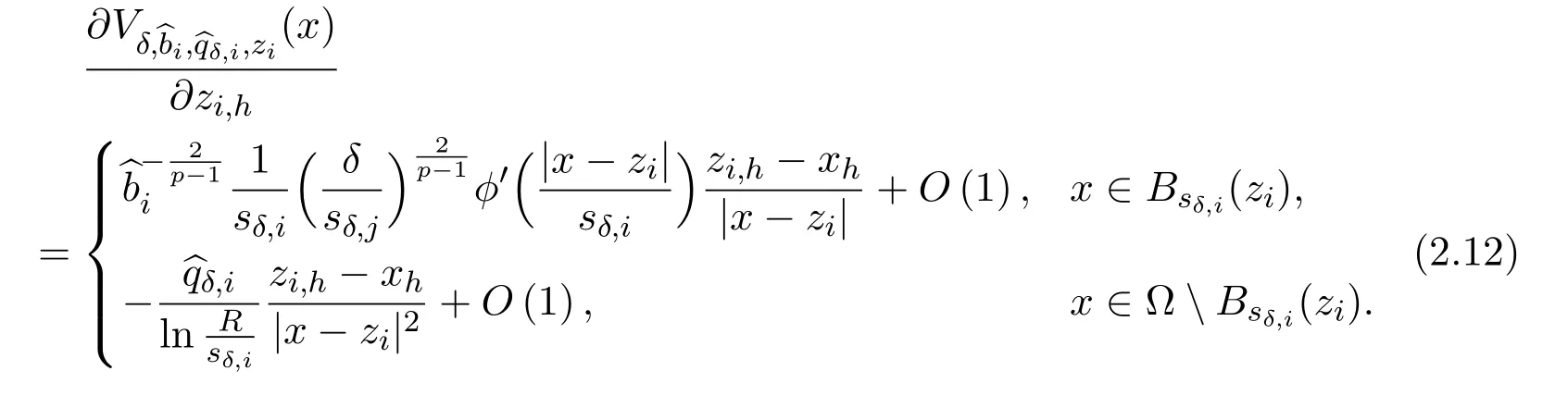
3 The Reduction
LetVδ,Zbe given as in(2.10),we are to find solutions to the formVδ,Z+ωδ,Z,whereωδ,Zis a small perturbation(obtained in Proposition 3.2).We will show that for any givenZ,there exists anωδ,Zsuch thatwδ,Z=Vδ,Z+ωδ,Zsatisfies
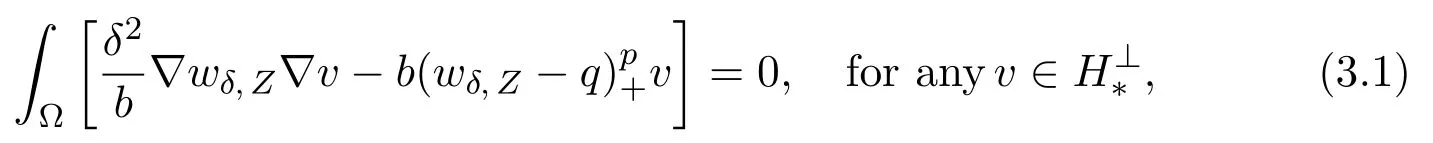
whereH∗is a finite dimension subspace of(Ω)∩W2,p(Ω).In the next section,we will chooseZproperly so thatVδ,Z+ωδ,Zis a solution to(1.4).
To show(3.1),we need to study the kernel of Lw:=-δ2div()-pb(Vδ,Z-w.To do this first we need to understand the kernel of the linearized equation of

Let
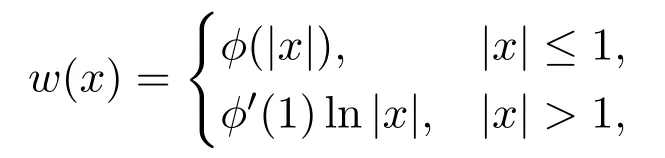
whereφis the solution to(2.3),thenw∈C1(R2)is the unique solution to(3.2).Sinceφ′(1)<0 and ln|x|is harmonic for|x|>1. Moreover,sincew+is Lipcontinuous,by the Schauder estimate,w∈C2,αfor anyα∈(0,1). Ifpis large enough,we can get better regularity ofw,e.g.,w∈Ck,α,p >k+α.
The linearized equation of(3.2)atwis as follows
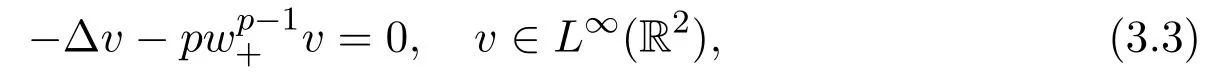
LetVδ,Z,jbe the function defined in(2.10).Set
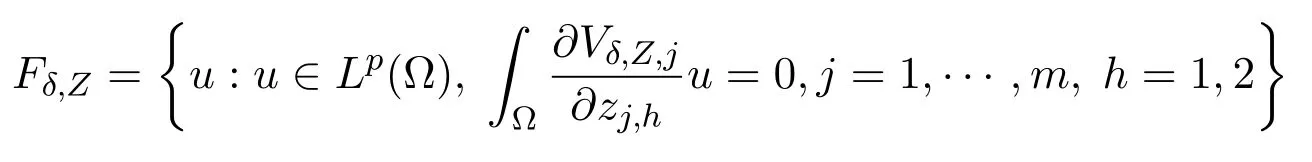
and
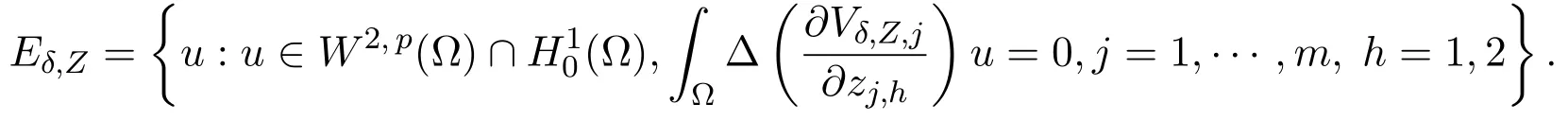
For anyu∈Lp(Ω),we need to make a projection fromLp(Ω)toFδ,Zwith respect to,j=1,···,m,h=1,2.To this end,defineQδuas follows:
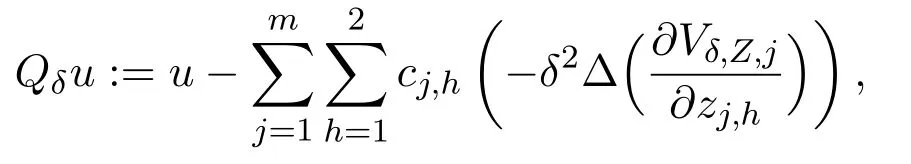
where the constantscj,h(j=1,···,m,h=1,2)depending onZ,δare chosen to satisfy
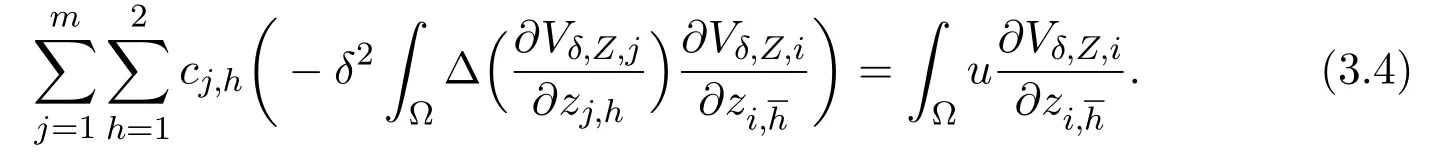
In order to show the existence ofcj,hsatisfying(3.4),we just need the following estimate(by(2.12)):
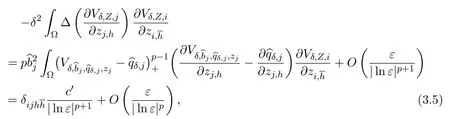
wherec′>0 is a constant,=1,ifi=jandh=;otherwise,=0.Set
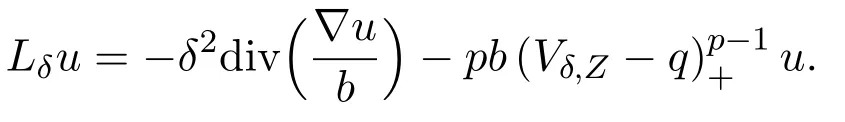
To obtain the invertibility of the linearized operatorQδLδ,we need the following lemma.
Lemma 3.1There are constants ρ0>0and δ0>0,such that for any δ∈(0,δ0],Z satisfying(2.8),u∈Eδ,Zwith QδLδu=o(1)inΩfor some L >0large,then
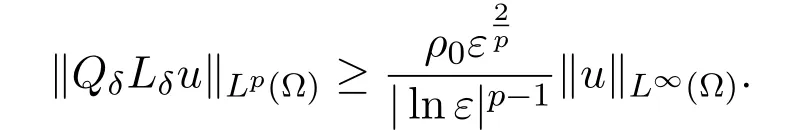
ProofSetsn,j=sδn,j.We will use ‖·‖p,‖·‖∞to denote ‖·‖Lp(Ω)and ‖·‖L∞(Ω)respectively.
We argue by contradiction.Suppose that there areδn→0,Znsatisfying(2.8)andun∈Eδn,ZnwithQδnLδnun=0 in Ω,such that
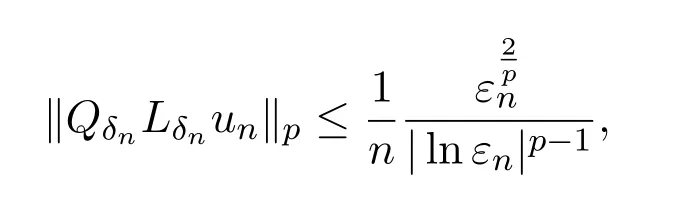
and ‖un‖∞=1.
Firstly,we estimatecj,h,nin the following formula:

For each fixedi,multiplying(3.6)bynoting that
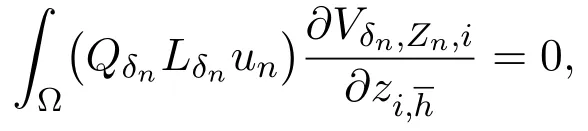
we obtain
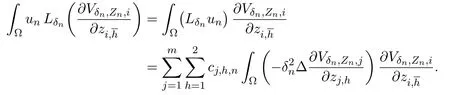
Using(2.11)and Lemma 6.1,we obtain
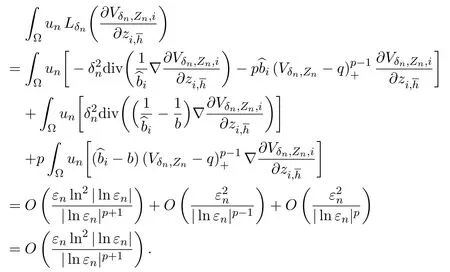
Using(3.5),we find that

Therefore,
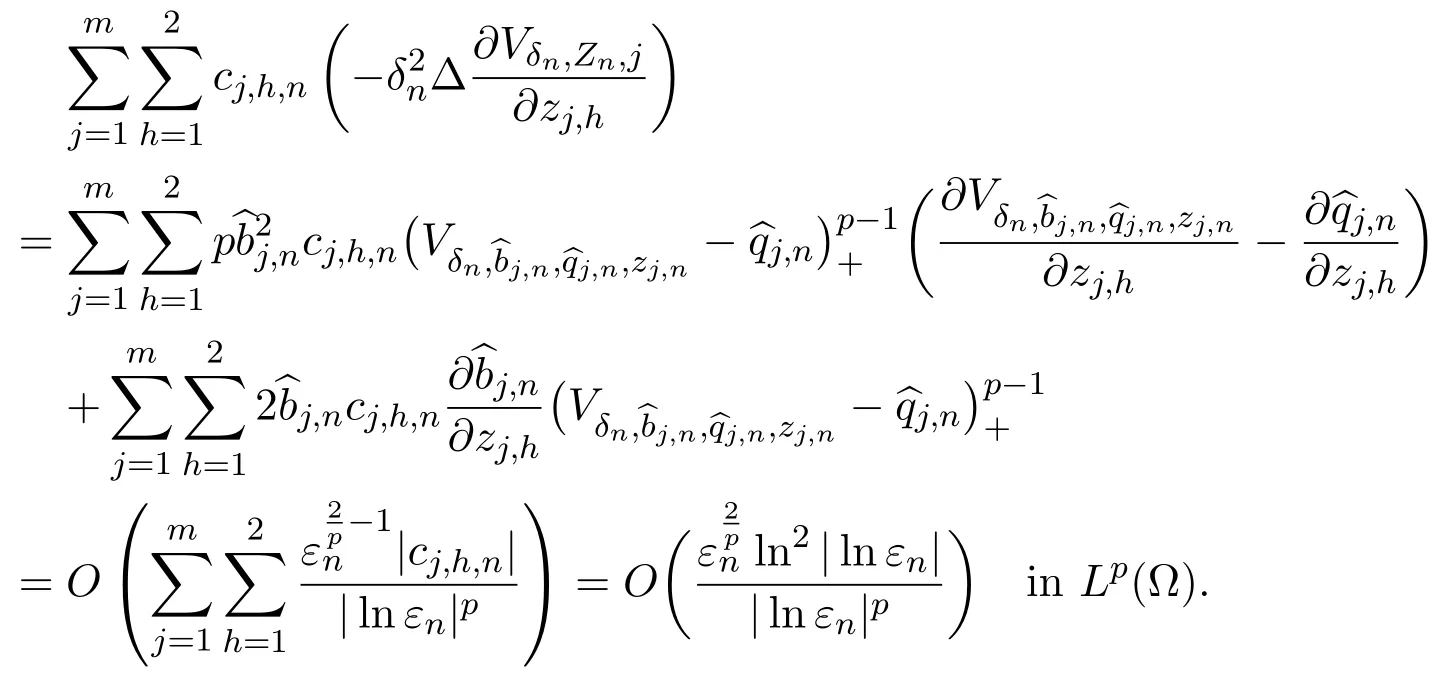
Thus,we obtain

For any fixedi,define(y)=un(sn,iy+zi,n).Let

Then

Noting that

we find that
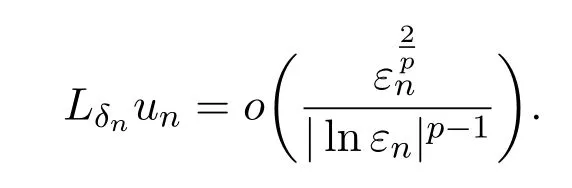
As a result,
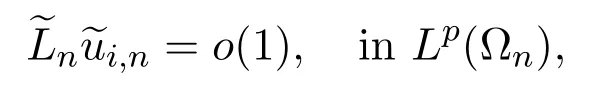
where Ωn=.
Thus,we may assume that
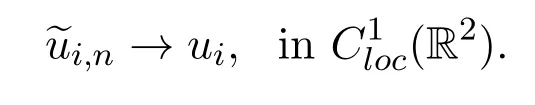
It is easy to see that
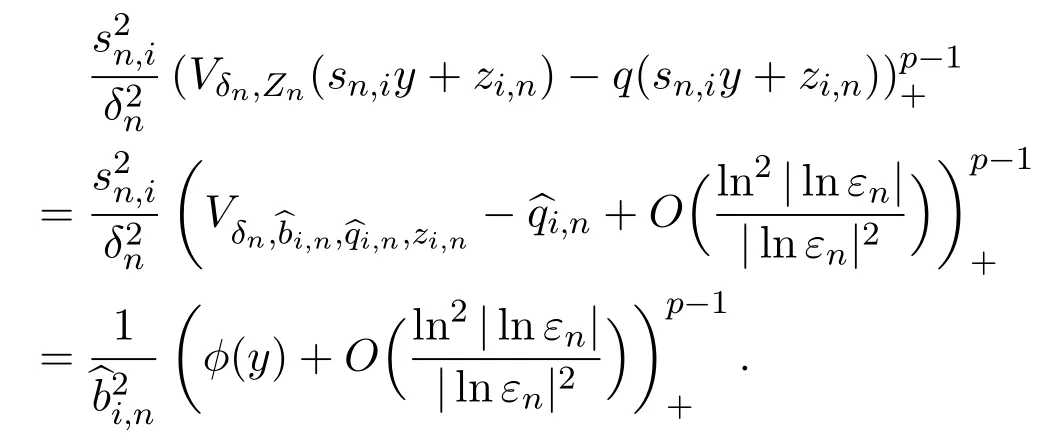
Then,by Lemma 6.1,we find thatuisatisfies
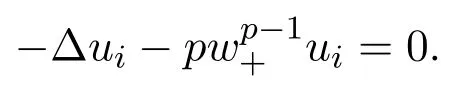
Now from Proposition 3.1 in[10],we have

Since
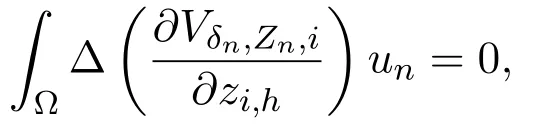
we find that
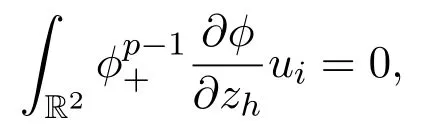
which,together with(3.7),givesui≡0.Thus,
for anyL >0,which implies thatun=o(1)on∂BLsn.i(zi,n).
By assumption,

On the other hand,by Lemma 6.1,forj=1,···,m,we have
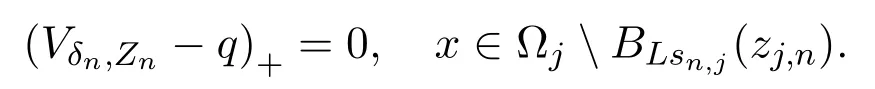
Thus,we find that
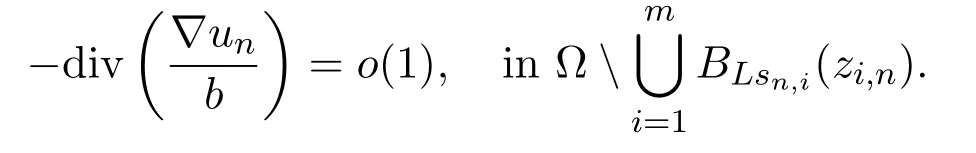
However,un=0 on∂Ω andun=o(1)on∂BLsn,i(zi,n),i=1,···,m.So we have
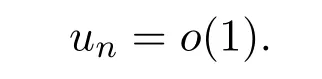
This is a contradiction.The proof is completed.
Proposition 3.1Under the same assumptions as in Lemma3.1,then QδLδu is one to one and onto from Eδ,Zto Fδ,Z.
ProofSuppose thatbQδLδu=0.Then,by Lemma 3.1,u=0.Thus,bQδLδis one to one.Next,we prove thatbQδLδis an onto map fromEδ,ZtoFδ,Z.
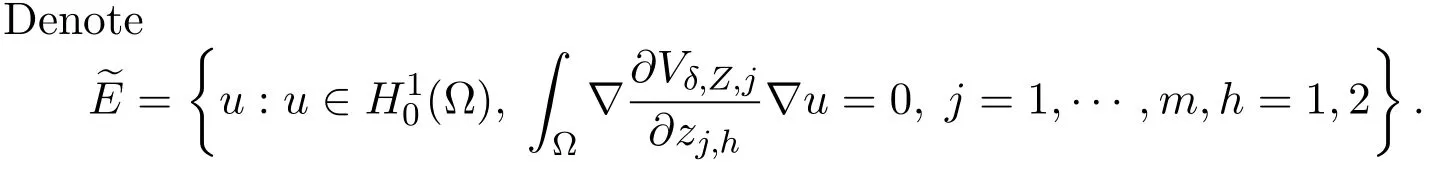
Note thatEδ,Z=∩W2,p(Ω).
For any~h∈Fδ,Z,by the Riesz representation theorem,there is a uniqueu∈(Ω),such that
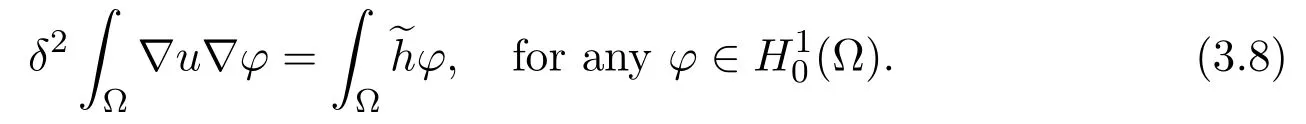
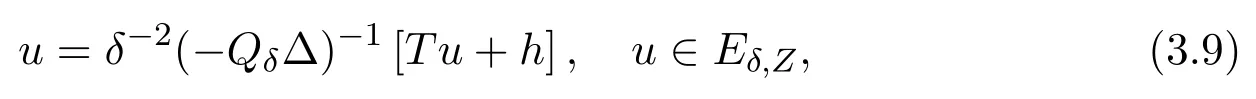
where

It is easy to check thatδ-2(-Qδ∆)-1Tuis a compact operator inEδ,Z.By the Fredholm alternative,(3.9)is solvable if and only if
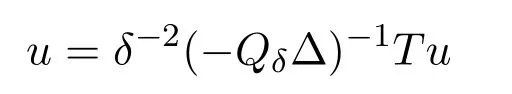
has only trivial solution,which is true sincebQδLδis a one to one map.The proof is completed.
Now consider the equation
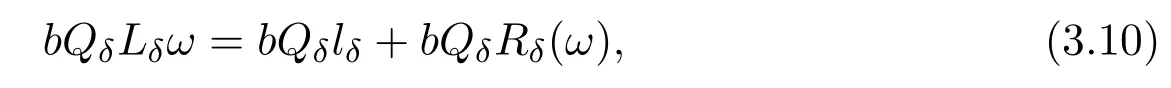
where
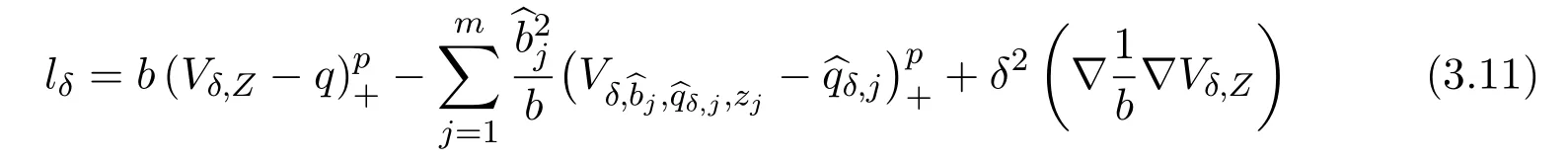
and

Using Proposition 3.1,we can rewrite(3.10)as

The next Proposition enables us to reduce the problem of finding a solution to(1.4)to a finite dimensional one.
Proposition 3.2There is a δ0>0,such that for any δ∈(0,δ0]and Z satisfying(2.8),(3.10)has a unique solution ωδ,Z∈Eδ,Z,with
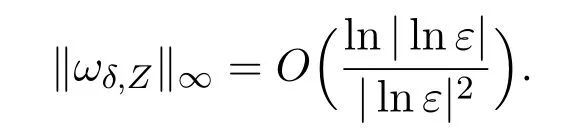
ProofIt follows from Lemma 6 that ifLis large enough andδis small,then
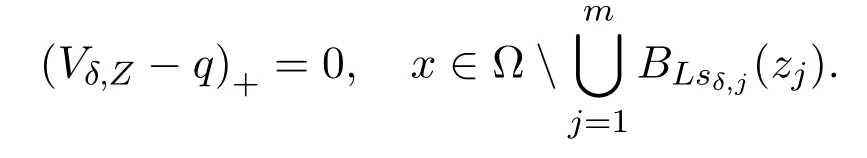
Let

whereθ >0 is a small constant.
ThenMis complete underL∞norm andGδis a map fromEδ,ZtoEδ,Z.We will show thatGδis a contraction map fromMtoMby two the following steps.
Step 1Gδis a map fromMtoM.
For anyω∈M,similar to Lemma 6.1,it is easy to prove that for largeL >0,δsmall
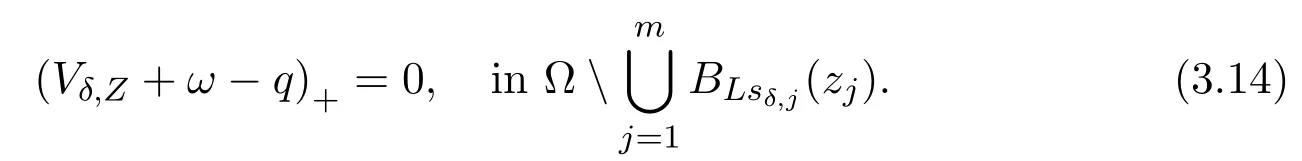
Note also that for anyu∈L∞(Ω),
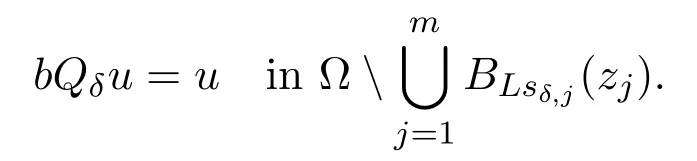
Direct computations yield that
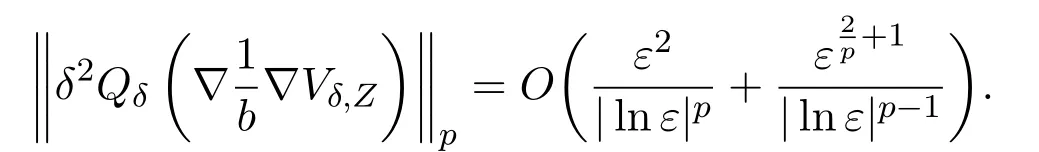
Therefore,using Lemma 6.1,(3.11)and(3.12),we find that for anyω∈M,
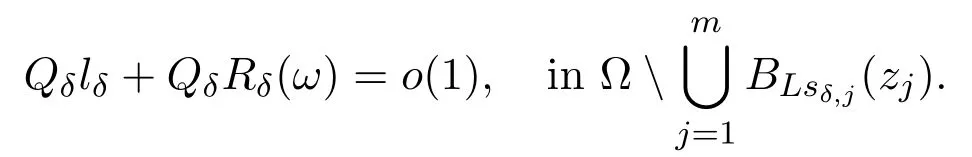
So,we can apply Lemma 3.1 to obtain
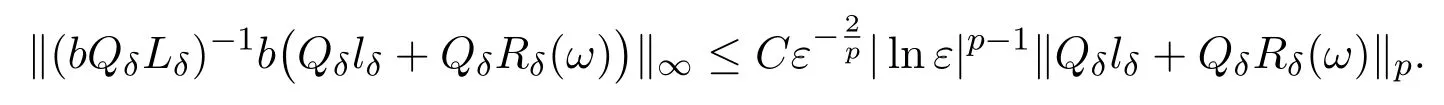
Thus,for anyω∈M,we have
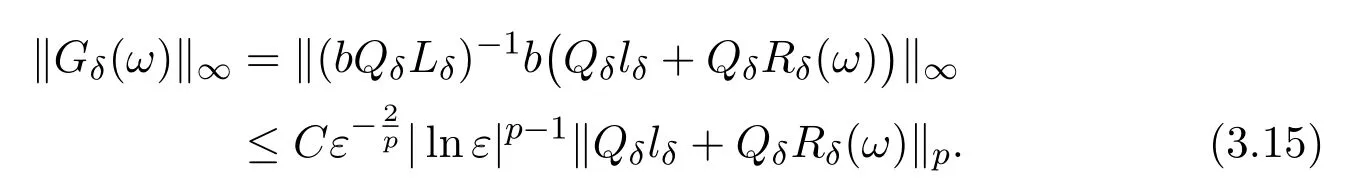
It follows from(3.4),(3.5)that the constantcj,h,corresponding tou∈L∞(Ω),satisfies
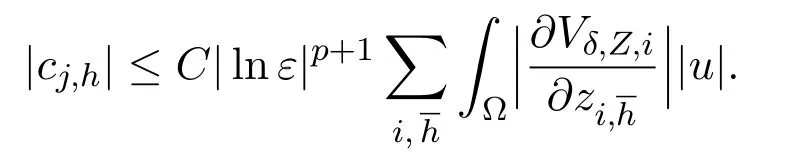
Hence,we find that the constantcj,h,corresponding tolδ+Rδ(ω)satisfies
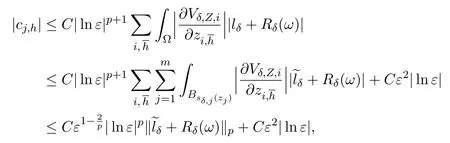
where
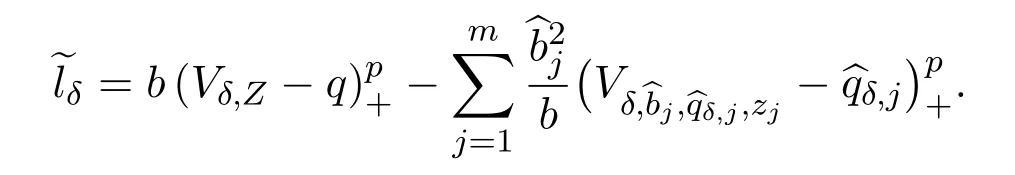
As a consequence,
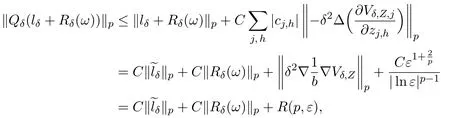
where
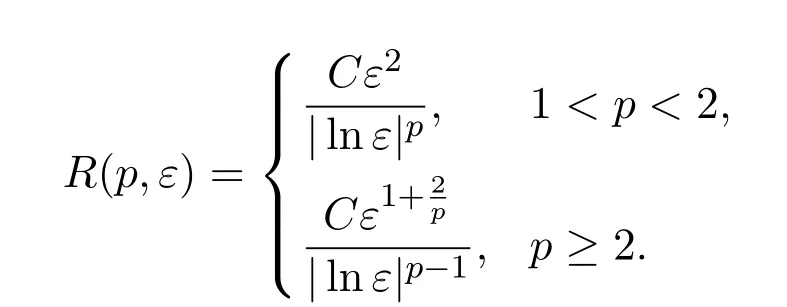
On the other hand,from Lemma 6.1 and(2.11),we can deduce
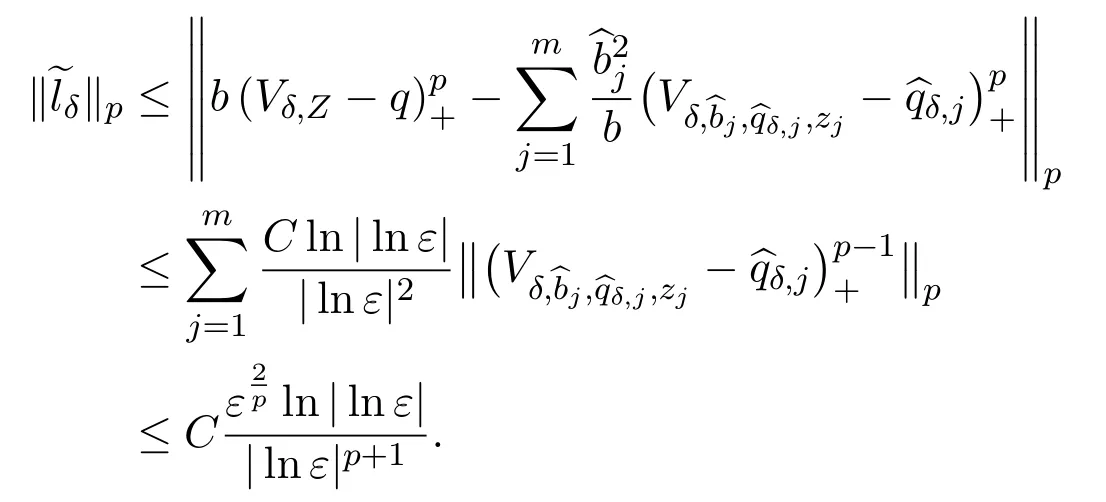
For the estimate of ‖Rδ(ω)‖p,we have
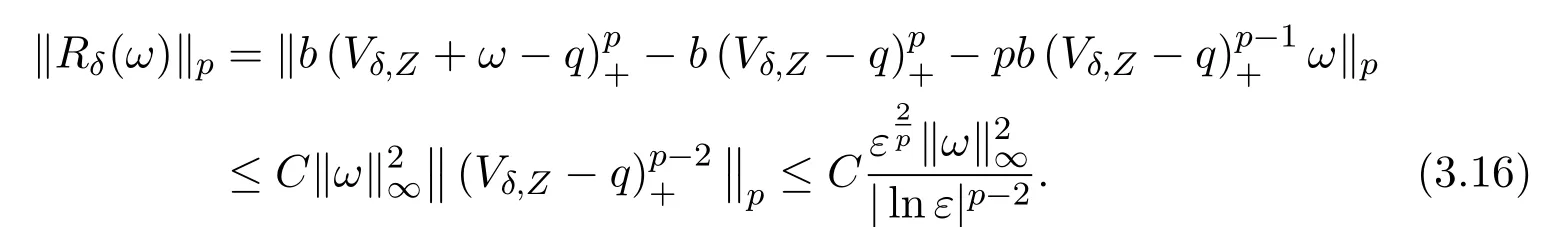
Thus,we obtain
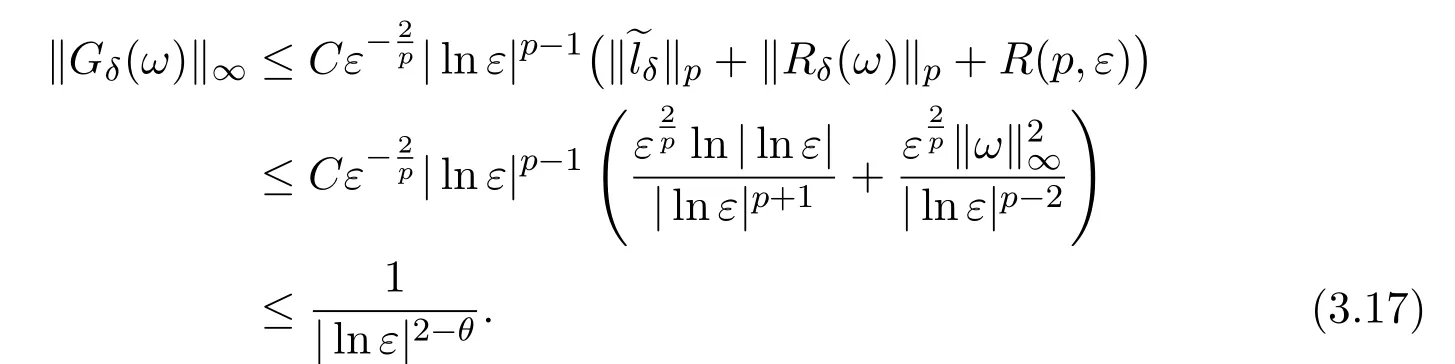
Thus,Gδis a map fromMtoM.
Step 2Gδis a contraction map.
In fact,for anyωi∈M,i=1,2,we have
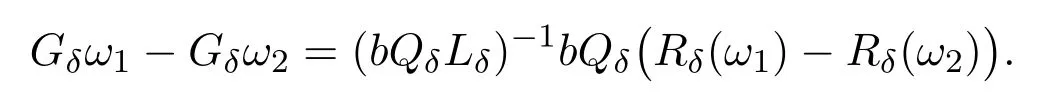
Noting that
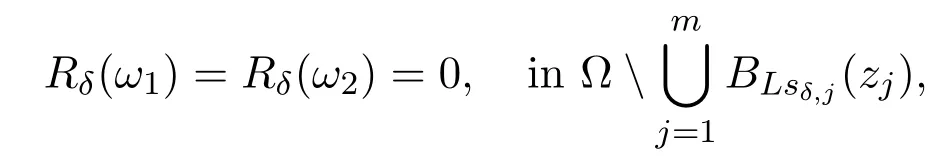
we can deduce as in Step 1 that
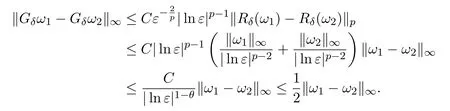
Combining Steps 1 and 2,we see thatGδis a contraction map fromMtoM.As a consequence,there is a uniqueωδ,Z∈M,such thatωδ,Z=Gδωδ,Z.Moreover,it follows from(3.17)that
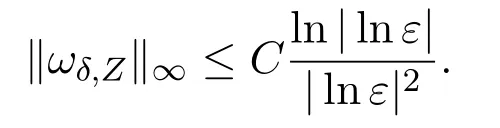
The proof is completed.
Remark 3.1It is worthwhile to point out that from Lemma 3.7 in[7],we also have thatωδ,Zis aC1-map ofZin the norm ofH10(Ω)since in our case the nonlinearity has better smoothness than in[7]and thus the argument is still applicable.
4 Proof of Main Results
In this section,we will give proofs for our main results.First,we will chooseZ,so thatVδ,Z+ωδ,Z,whereωδ,Zis the map obtained in Proposition 3.2,is a solution to(1.4).
Define
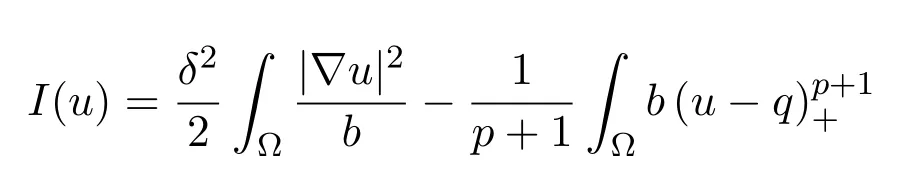
and

It follows from Remark 3.1 thatK(Z)is aC1function ofZ. Moreover,it is well known that ifZis a critical point ofK(Z),thenVδ,Z+ωδ,Zis a solution to(1.4).
We will prove thatK(Z)has a critical point. To do this we first find out the main part ofK(Z)as follows.
Lemma 4.1We have
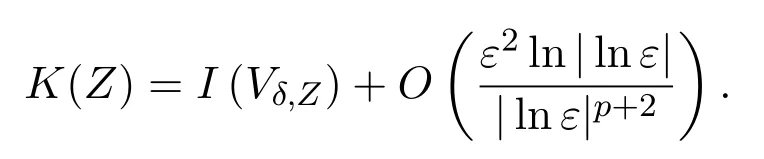
ProofRecall that
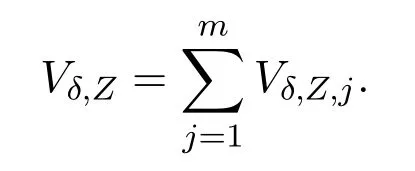
We find that
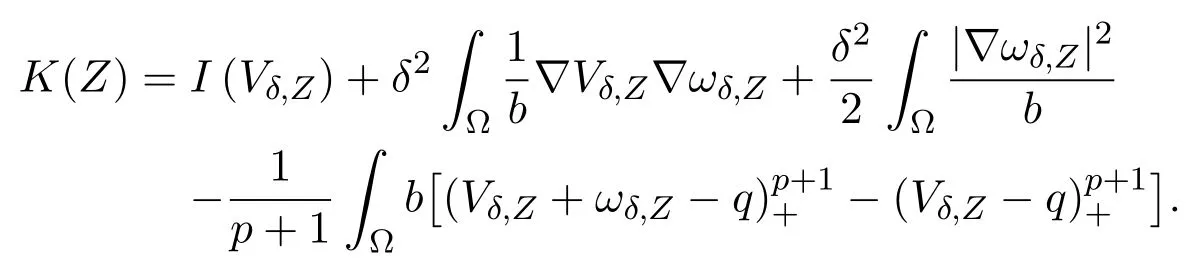
Using Proposition 3.2 and(3.14),we have
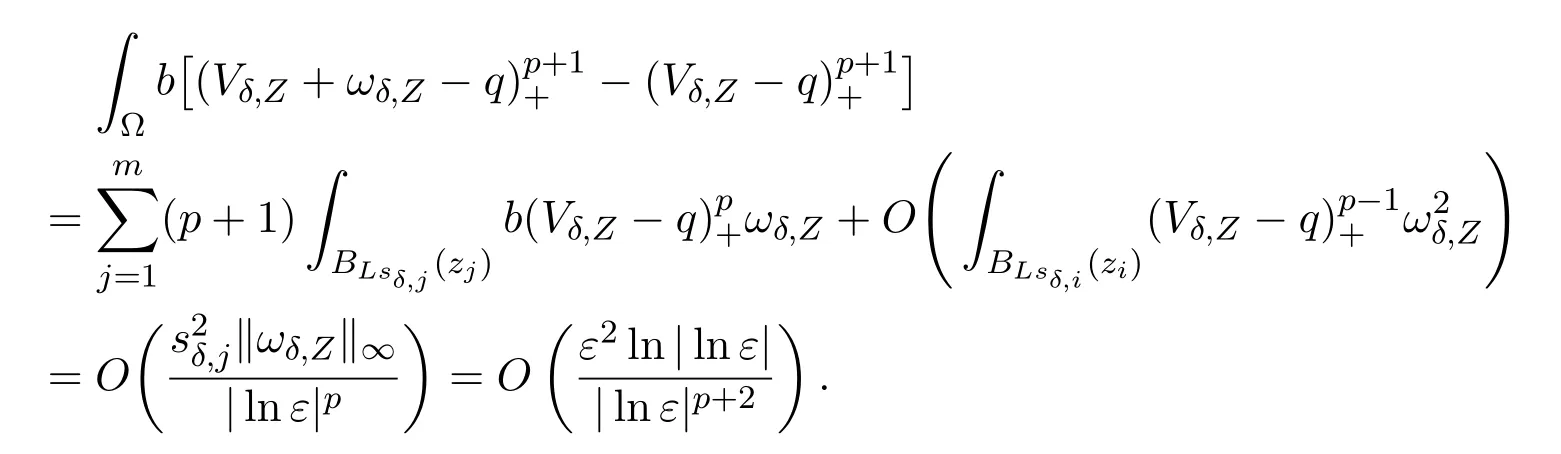
On the other hand,
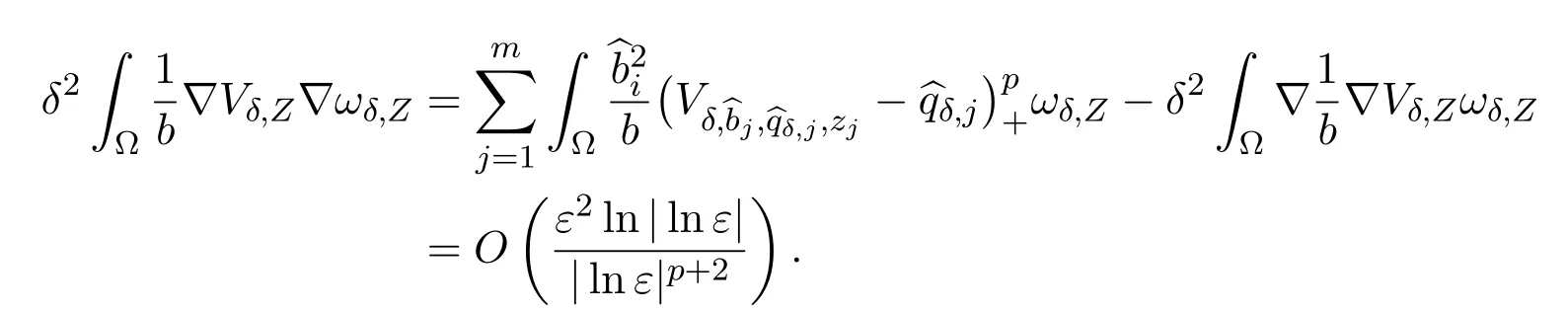
Note that
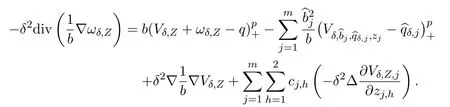
Hence,
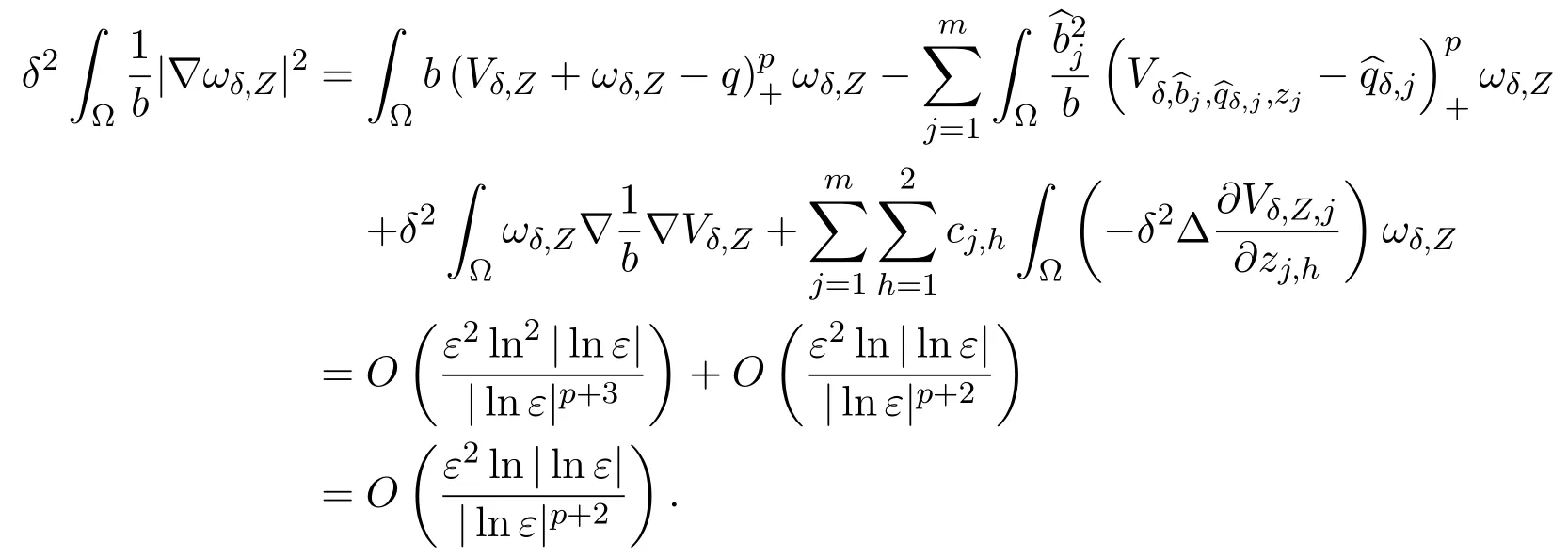
The proof is completed.
Proof of Theorem 1.3By Proposition 6.1,we have
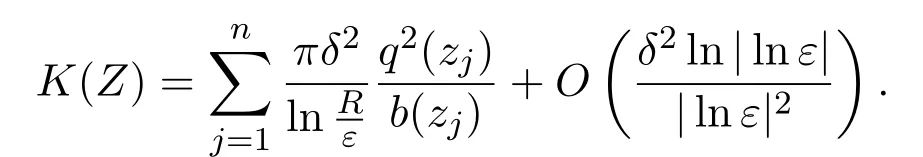
Proof of Theorem 1.4Define
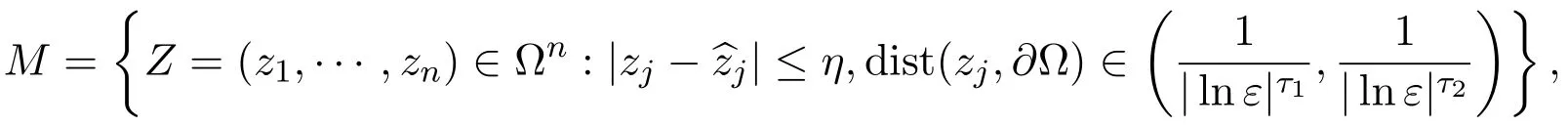
whereτ1andτ2will be determined later.
Consider
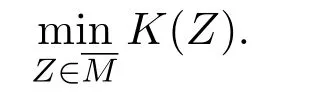
There exists a minimizerZεforK(Z)in.Now,as in Theorem 1.3,we just need to verify thatZεis an interior point ofMand hence is a critical point ofK(Z).
By Proposition 6.1,we have
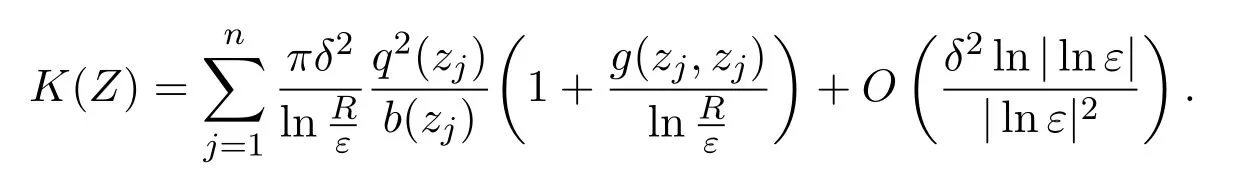
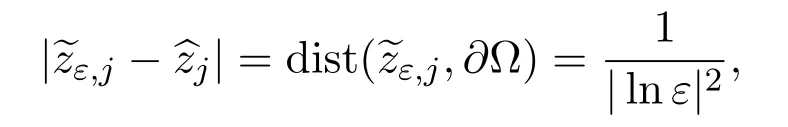
then
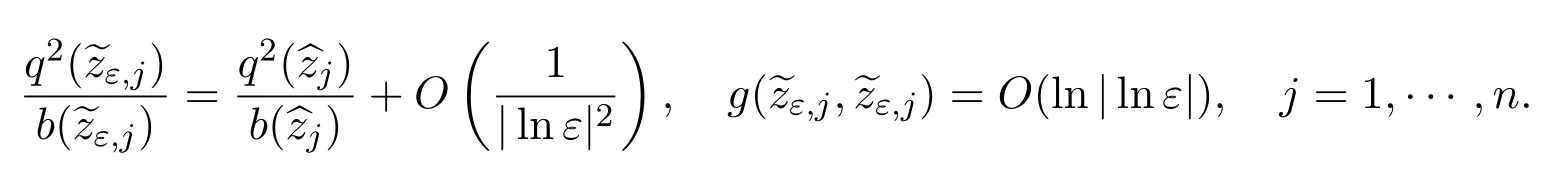
As a result,
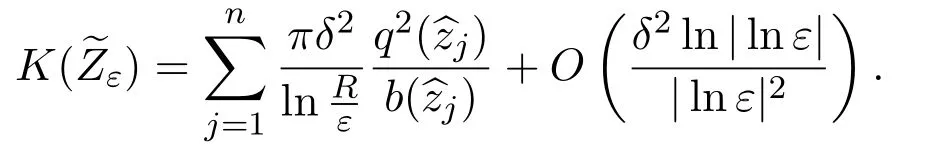
Note that
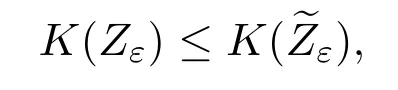
we find
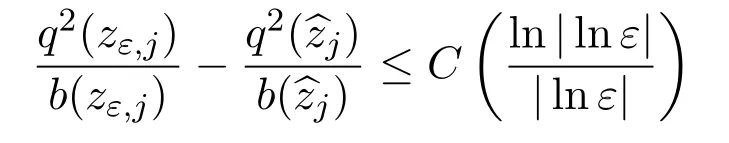
and
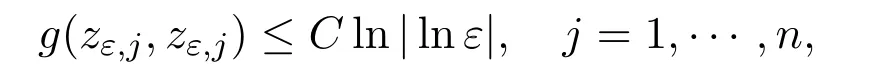
whereCis independent ofτ1andτ2.Hence,forj=1,···,n,we have
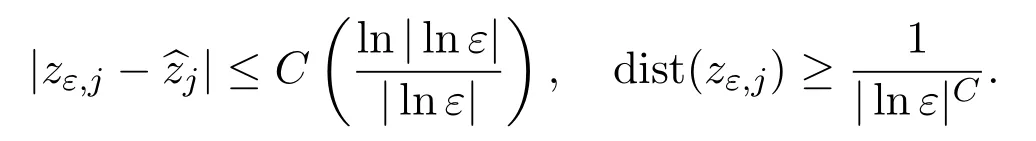
Thus,Zεis an interior point ofMif we chooseτ1to be sufficiently large andτ2sufficiently small in the definition ofM.The proof is completed.
Proof of Theorems 1.1 and 1.2By Theorems 1.3 and 1.4,we obtain thatuεis a solution to(1.3).
Define forx∈Ω
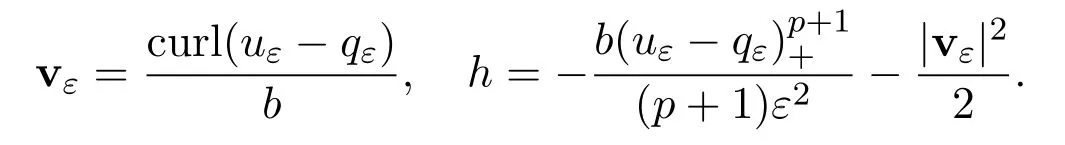
Then,vεis a stationary solution to(1.1)with
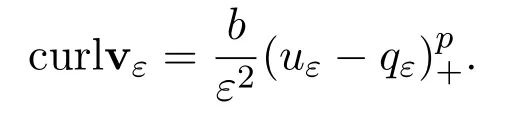
To finish our proof we only need to verify
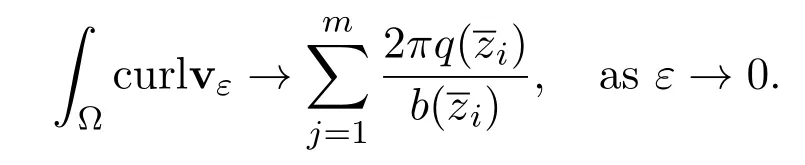
By direct calculations,we obtain
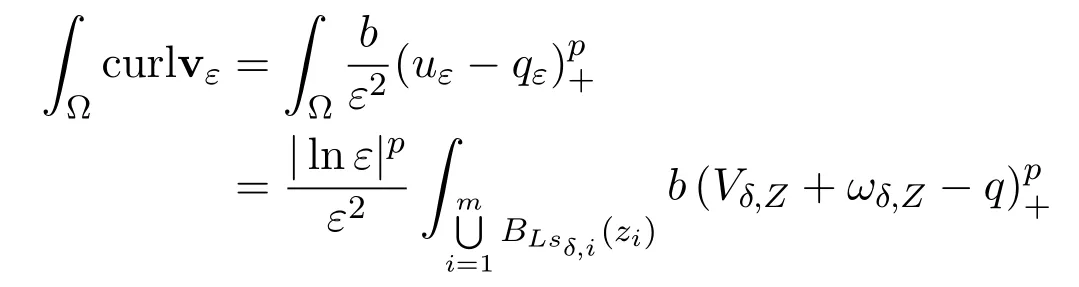

Therefore,the result follows.The proof is completed.
5 Further Results
In this section,we will use the idea and techniques in the previous sections to construct vortex pairs for the shallow water equations,which has not been addressed before.
Instead of(1.3),similar to[9],we now consider the following boundary value problem:
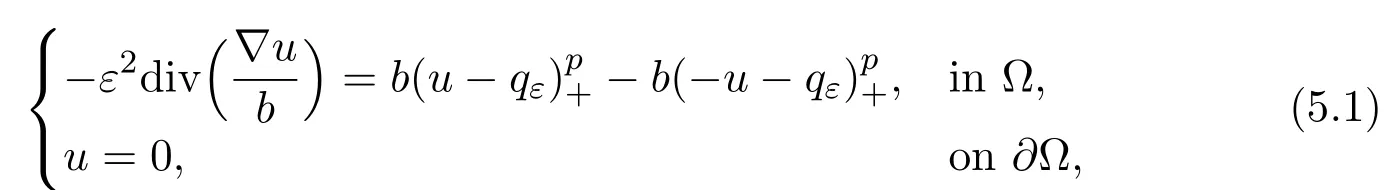
wherep >1,q=-ψ0,qε=qln,Ω ⊂R2is a smooth bounded domain.
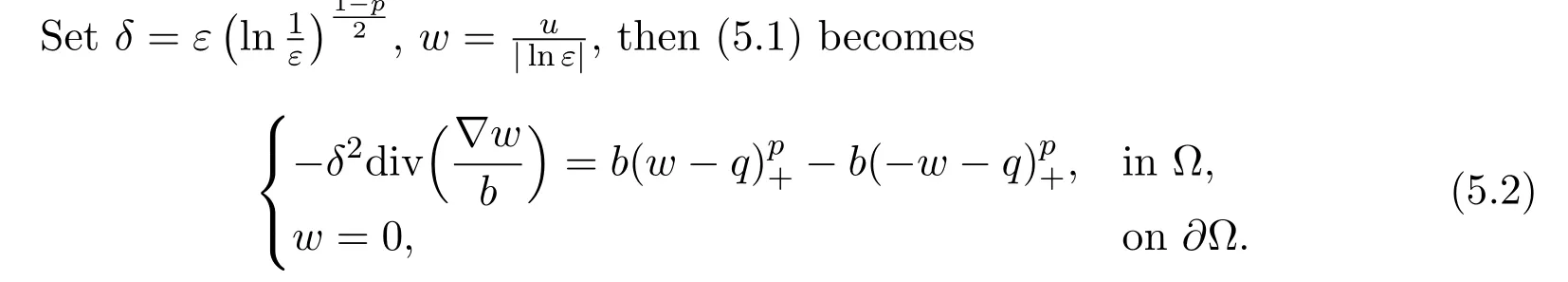
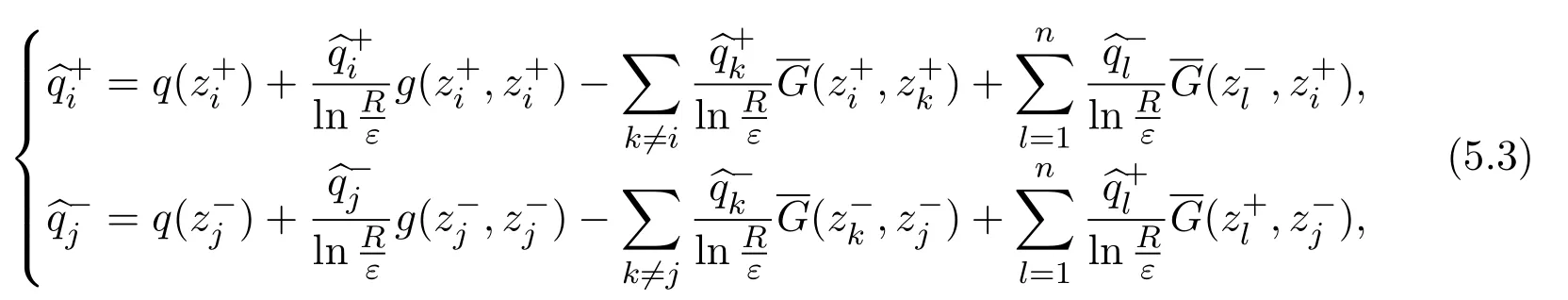
wherei=1,···,m,j=1,···,n.
Set
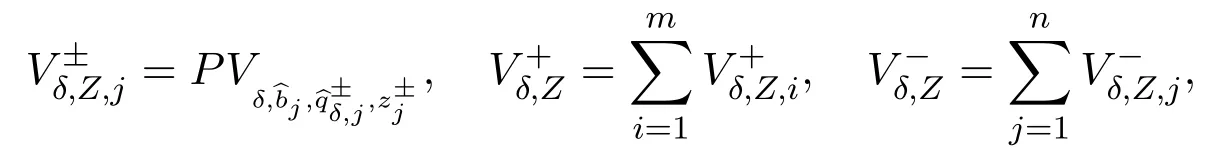
and
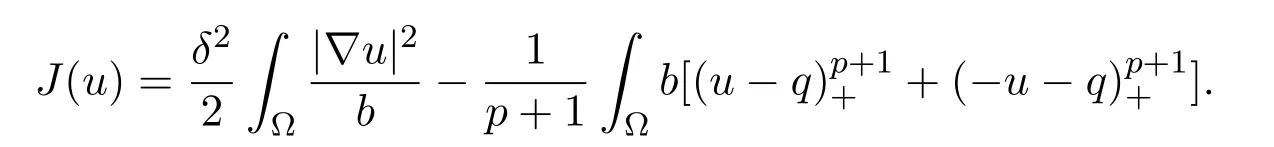
Letbe the solution to
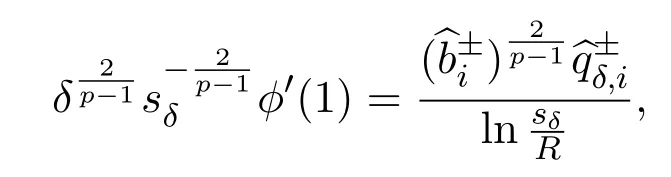
then,we have
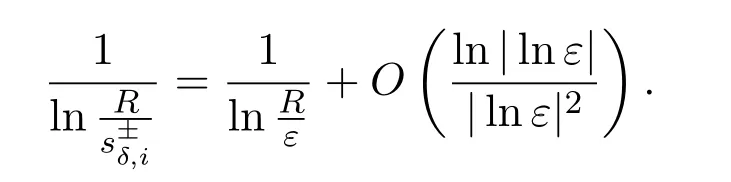
Thus,as in(2.11),we find,fori=1,···,mandj=1,···,nthat
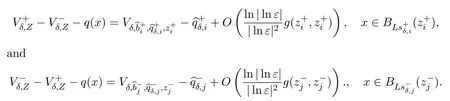
Similar to Proposition 6.1,we have the following energy expansion:
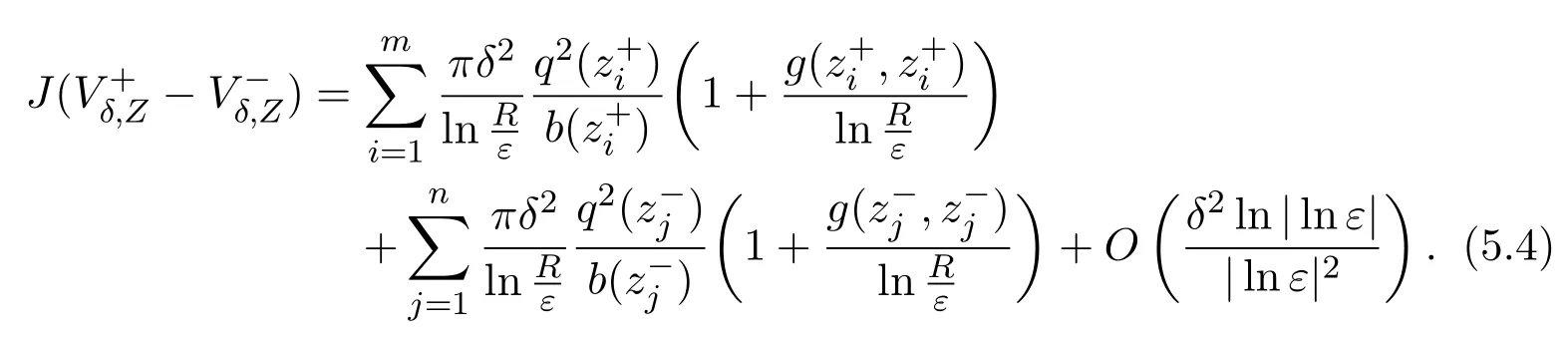
Theorem 5.1Suppose thatΩ ⊂R2is a smooth bounded domain. SupposeFrom(5.4),we can deduce the following results:thatb∈C2(),infΩb >0andsupΩψ0<0satisfying-div=0. Then,forany given strictly local minimum(maximum)points?,·····,of,there exists an ε0>0,such that for each ε∈(0,ε0),there exists a family solutionsvε∈C1(Ω,R2)and hε∈C1(Ω)of
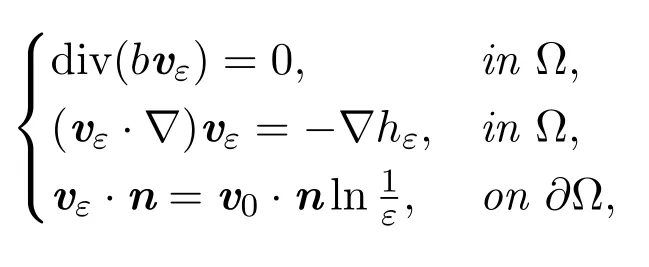
such that its vorticity ωε:=curlvεsatisfying
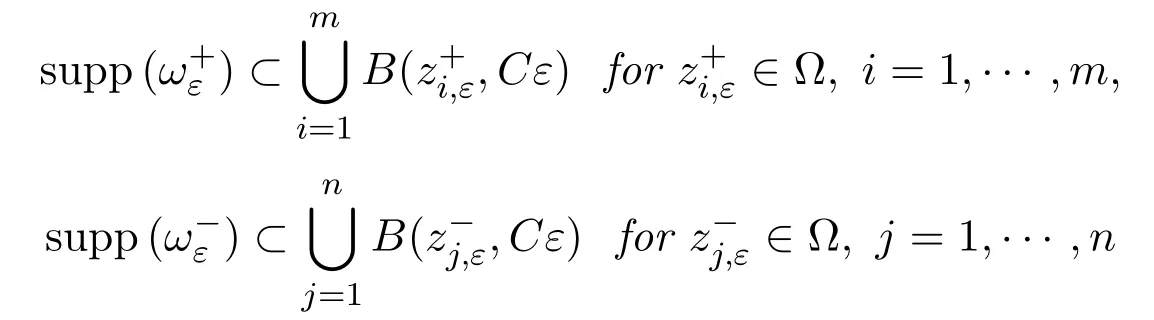
and as ε→0,
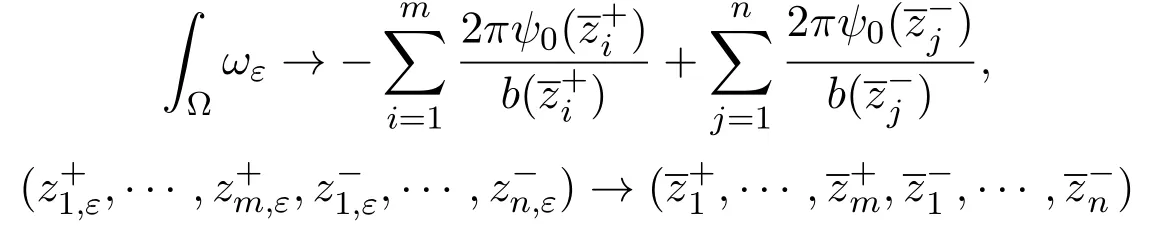
wherenis the outward normal direction of ∂Ω,C is a positive constant.
ProofLetωδ,Zbe the map obtained in the reduction procedure.Define
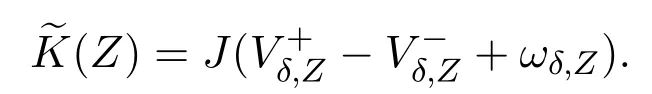
Then,as in Lemma 4.1,we can prove
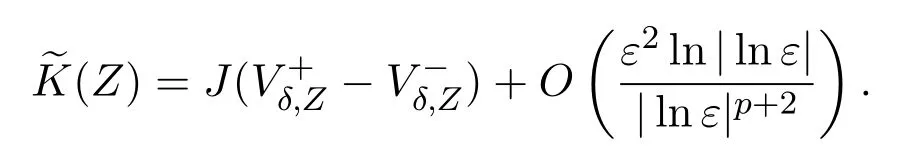
Similar to Theorem 1.3,we can obtain a solutionuεto(5.1).
Define forx∈Ω
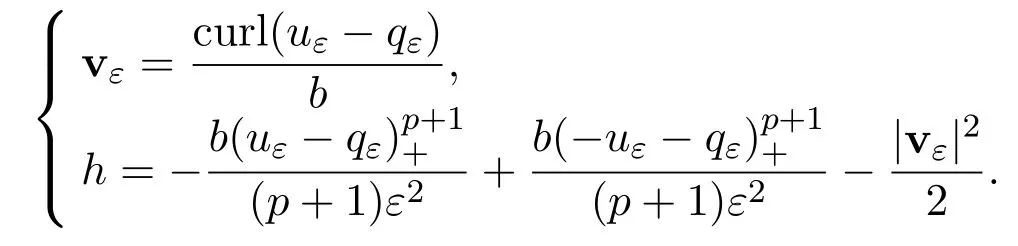
Thus,vεis a stationary solution to(1.1)with
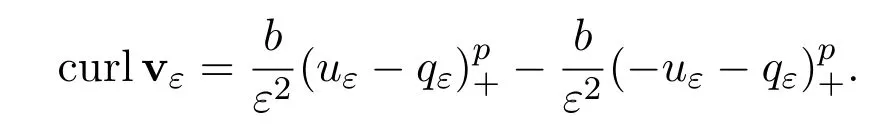
Now,as in Theorem 1.1,we find
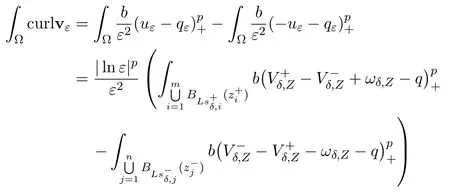
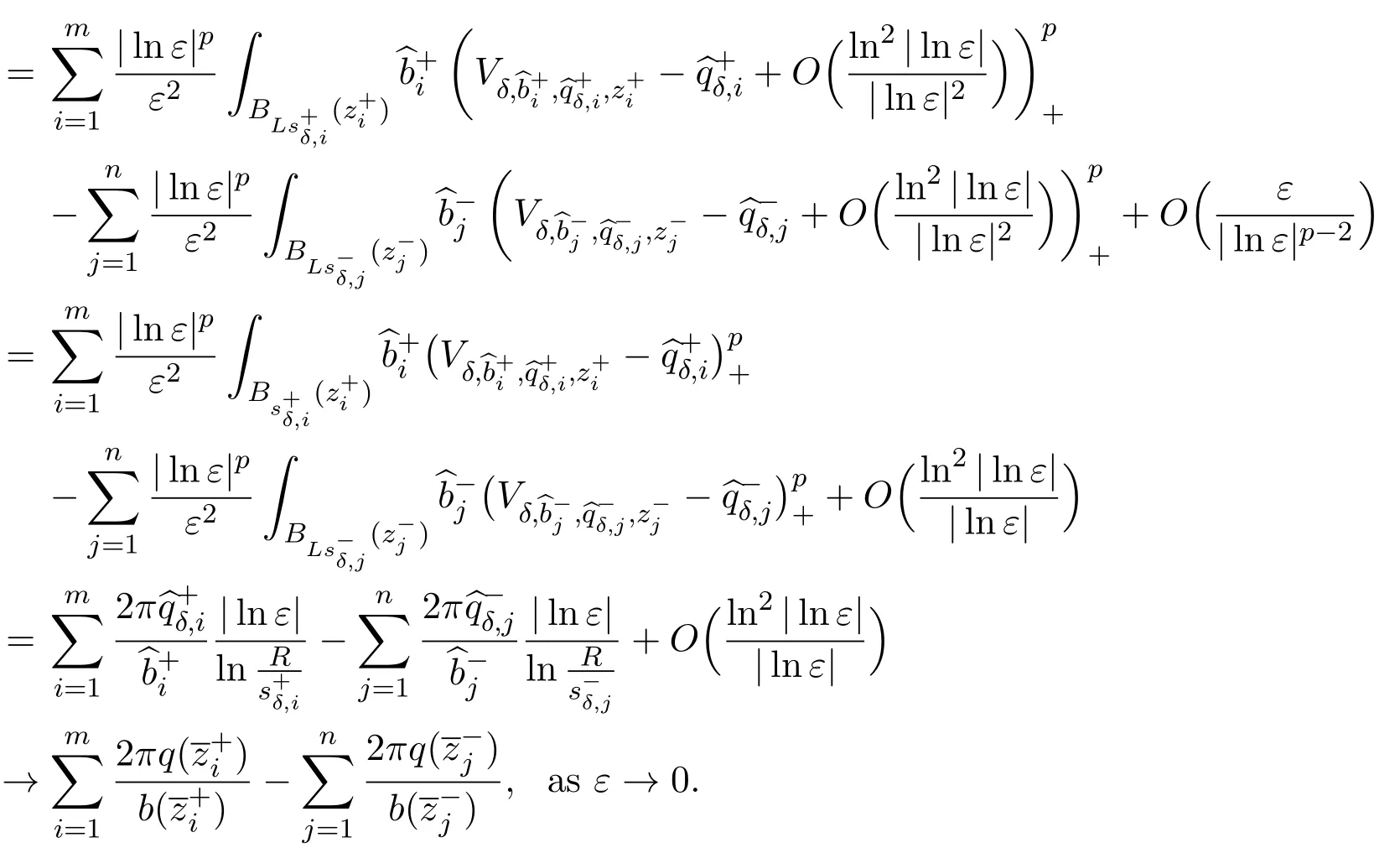
So,the result follows.
Remark 5.1For any given strictly local minimum points,···,,···,ofon the boundary∂Ω,we can also obtain the corresponding results as in Theorem 1.2.
6 Technical Estimates
In this section we will give precise expansions ofI(Vδ,Z),which has been used in Section 4.Let

Recall that
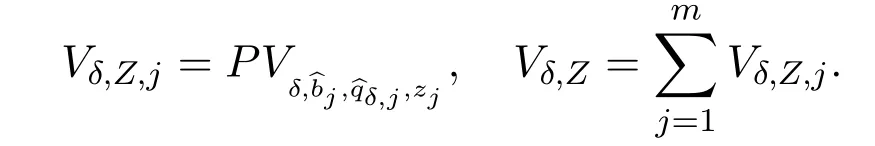
Lemma 6.1There is a large constant L >0such that
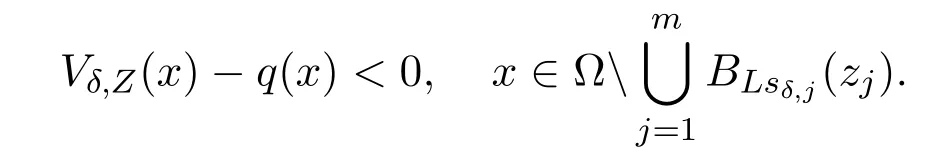
ProofThe proof is similar to that of Lemma A.1 in[10].For convenience,we only give a sketch here.
Ifσ >0 is small and|x-zj|≥,j,j=1,···,m,
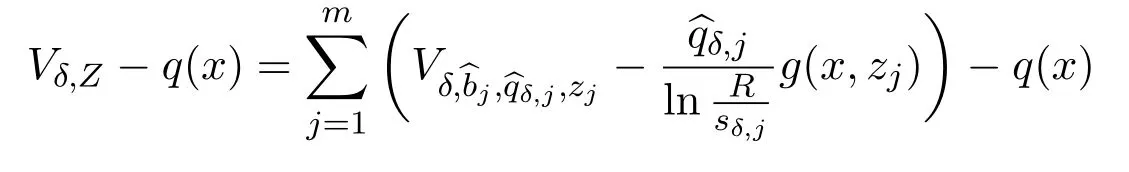
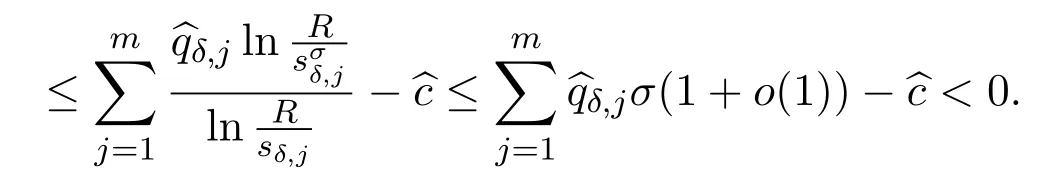
IfLsδ,j≤|x-zj|≤,then it follows from(2.11)that
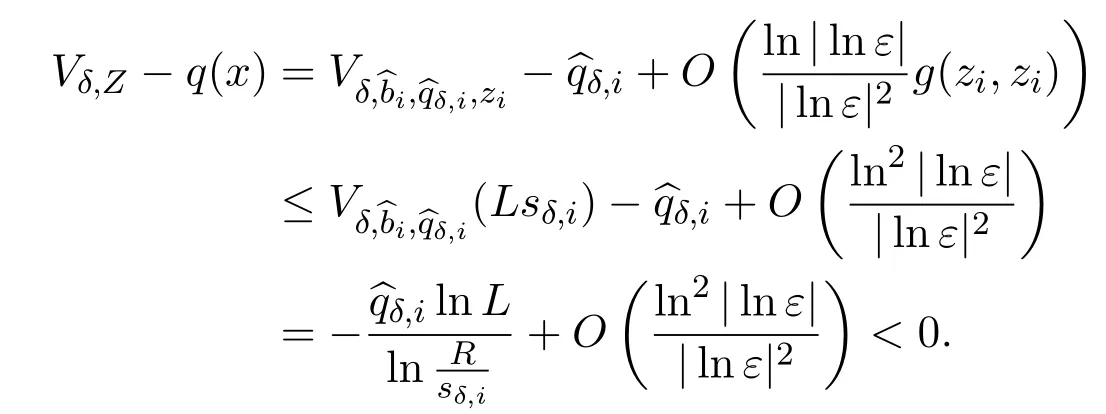
The proof is completed.
Proposition 6.1We have
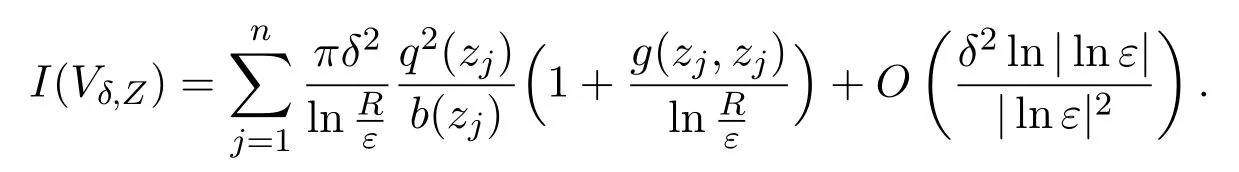
ProofTaking advantage of(2.6),we find that

First,we estimate
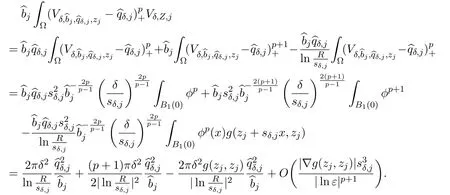
Next,forj̸=i,
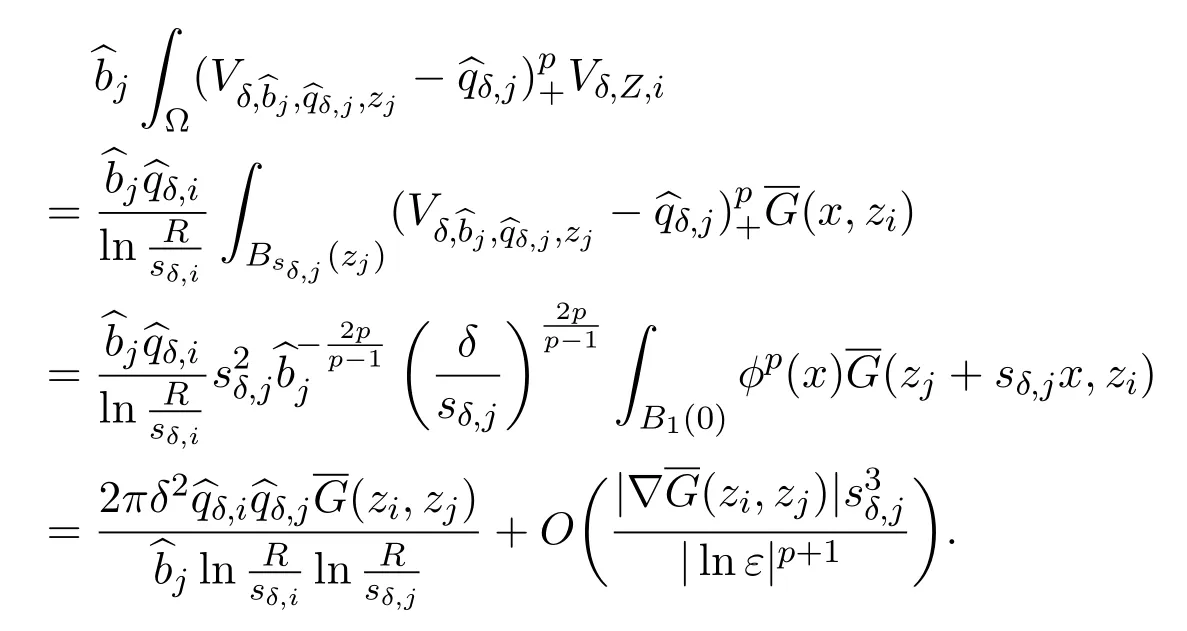
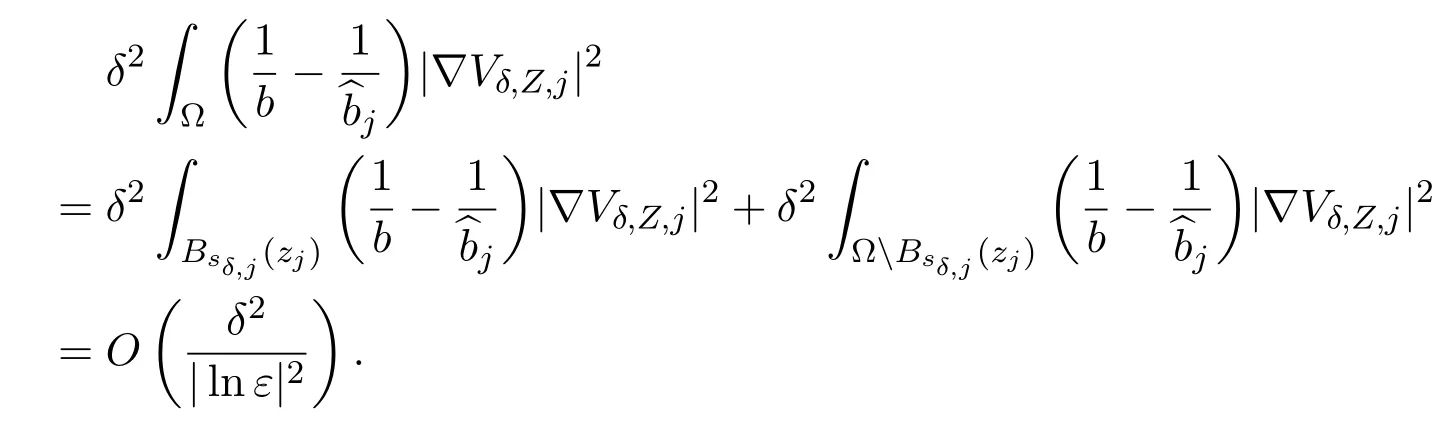
Similarly,
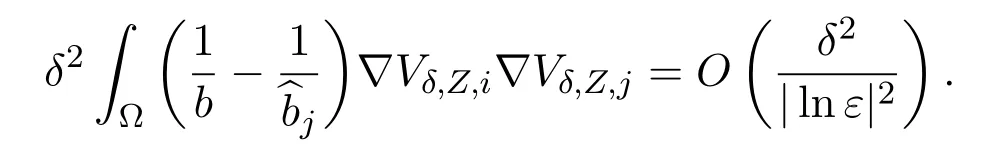
By Lemma 6.1,we have

Thus,we find
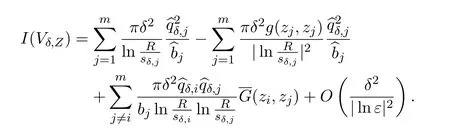
The result follows from the fact that

The proof is completed.
