LIPSCHITZ CONTINUITY OF MINIMIZERS FOR THE GINZBURG-LANDAU FUNCTIONAL BETWEEN ALEXANDROV SPACES∗†

Jia-Cheng Huang, Hui-Chun Zhang

(Dept.of Math.,Sun Yat-sen University,Guangzhou 510275,Guangdong,PR China)

Abstract In this paper,we shall prove that any minimizer of Ginzburg-Landau functional from an Alexandrov space with curvature bounded below into a nonpositively curved metric cone must be locally Lipschitz continuous.

Keywords Ginzburg-Landau functional,Alexandrov space,NPC metric space

1 Introduction

LetNbe a positive integral and Ω be a bounded domain in a smooth Riemannian manifold. For fixedK ＞0,recall that the Ginzburg-Landau functionalIK(·)onW1,2(Ω,RN)is defined by

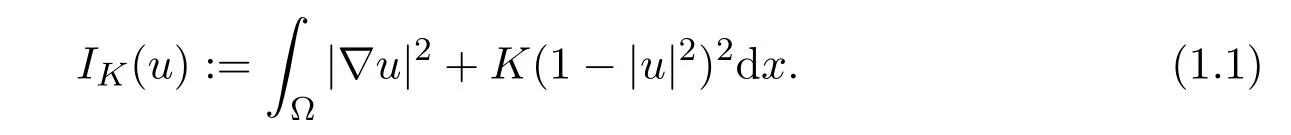
This kind of functionals has been originally introduced as a phenomenological phase-field type free-energy of a superconductor.The Ginzburg-Landau functionals have deserved a great attention by the mathematical community too.Starting from the classical monograph[2](see also[1])by Bethuel,Brezis and H´elein,many mathematicians have been interested in studying minimization problems for the Ginzburg-Landau energy on smooth manifolds.We refer the readers to,for instance,[1,2,27]and references therein for this topic.

In this paper,we will study the Ginzburg-Landau functional from an Alexandrov space with curvature bounded below(shortly,CBB)into a non-positively curved(shortly,NPC)metric space.Roughly speaking,an Alexandrov space with CBB is a length spaceXwith the property that any geodesic triangle inXis“fatter”than the corresponding one in the associated model space.The seminal paper[4]and the 10th chapter in the book[5]provide introductions to Alexandrov geometry.

Let us begin from the concept of energy for maps between metric spaces,which was introduced by N.Korevaar and R.Schoen in[23].Let(X,|·,·|),(Y,d)be two metric spaces and Ω be a bounded domain(connected open subset)ofX.µis a Radon measure onX.Givenp≥1,ε ＞0 and a Borel measurable mapu:Ω →Y,the approximating energy functionalofuis given as follows.For each compactly supported continuous functionφ∈Cc(Ω),we set

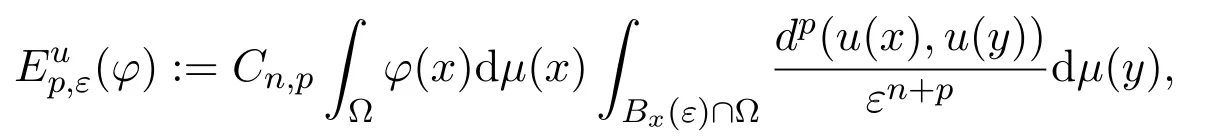
whereCn,pis a normalized constant.Thep-th energy functional ofuis defined by

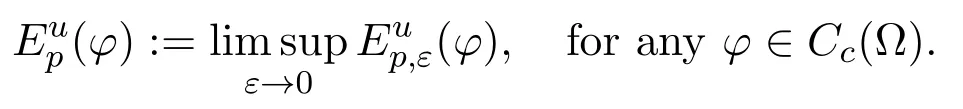
We say thatu∈W1,p(Ω,Y)ifu∈Lp(Ω,Y)and it has finitep-energy

Let(Y,dY)be an Euclidean cone with the vertexoand Ω be a domain ofX.GivenK ＞0,now one can define the Ginzburg-Landau functional,IKonW1,2(Ω,Y)as

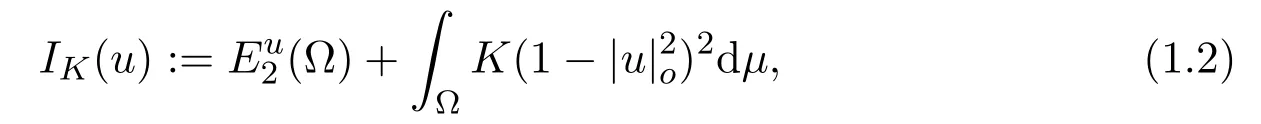
where|u|o:=dY(u,o)for anyu∈Y.We also write|·|instead of|·|ofor short.We say thatu∈W1,2(Ω,Y)is a minimizer of(1.2),if for anyv∈W1,2(Ω,Y)withd(u,v)∈(Ω),we haveIK(u)≤IK(v).

The purpose of this paper is to study the regularity theory of minimizers for the Ginzburg-Landau functionIKfrom a domain of an Alexandrov space with CBB into a complete NPC length space.IfK=0,a minimizer ofIKis a harmonic map.In this case,this problem was initiated by F.H.Lin[26]and J.Jost[15-18],independently.They established the locally H¨older continuity for harmonic maps from a domain of an Alexandrov space with CBB into a complete NPC length space.In fact,one can modify their arguments in[17,26]to deduce the locally H¨older continuity for minimizers of the Ginzburg-Landau functionIK,for anyK ＞0,under the same setting.

Similar as the harmonic maps between singular spaces,an interesting problem is to extend the above H¨older regularity to Lipschitz continuity.In this direction,Serbinowski[35]established the following result.

Theorem 1.1Let K ＞0andΩbe a bounded domain of a smooth manifold M.Assume that uKis a minimizer of IKfromΩinto the Euclidean cone Y=C(Z)over a metric space Z with curvature(Z)≤1. Suppose that|uK(x)|≤1for any x∈∂Ω.Then uKis locally Lipschitz continuous interiorΩ.

However,the Lipschitz constant in Theorem 1.1 depends on theC1-norm of the metric(gij)of the manifoldM.So,the argument in[35]is not available to obtain the Lipschitz continuity for a minimizer ofIKfrom Alexandrov spaces with CBB.

Recently,the locally Lipschitz regularity for harmonic maps from a domain of an Alexandrov space with CBB into a complete NPC length space has been proved by the second author and Zhu in[40].

In this paper,we will extend the method in[40]to the minimizers of the Ginzburg-Landau functionalIK,and prove the following locally Lipschitz result.

Theorem 1.2Let K ＞2.Let X be an n-dim Alexandrov space with curvature≥k with k≤0,andΩ ⊂X be a bounded domain.Let Y=C(Z)be the Euclidean cone over a complete locally compact geodesic space Z,with curvature(Z)≤1(in the sense of Alexandrov).o∈Y is the vertex of Y.Then every minimizer u of(1.2)with|u|≤1on ∂Ωis locally Lipschitz continuous interiorΩ.Precisely,for any ball Bq(R)with Bq(2R)⊂ Ω,there exists a constant C(n,k,R),depending only on n,k and R,such that

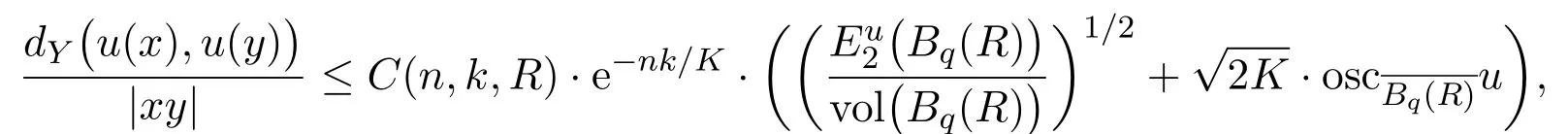
for all x,y∈Bq(R),where(Bq(R))is the energy of u on Bq(R).

Remark 1.1IfYis the Euclidean cone over a complete locally compact geodesic spaceZwith curvature(Z)≤1,thenYis an NPC space.

We also give a Lipschitz regularity result for the case where the target spaceYis a metric space with 2-sided curvature bounds,see Theorem 6.1.

Organization of the paper. In Section 2,we will provide some necessary materials on Alexandrov spaces,Sobolev spaces for maps. In Section 3,we will discuss some properties of minimizers for(1.2).In Section 4,we will prove the H¨older regularity via a method of[17]and an estimate for pointwise Lipschitz constant of the minimizers.The Lipschitz regularity result for the minimizers will be proved in Section 5.Finally,in Section 6,we will give a Lipschitz regularity result for the case where the target spaceYia a metric space with 2-sided curvature bounds.

2 Preliminaries

2.1 Alexandrov spaces

Letk∈R andl∈N.Denote bythe simply connected,l-dimensional space form of constant sectional curvaturek.The spaceis calledk-plane.

Let(X,|·,·|)be a complete metric space.A rectifiable curveγconnecting two pointsp,qis called ageodesicif its length is equal to|pq|and it has unit speed.A metric spaceXis called ageodesic spaceif,for every pair of pointsp,q∈X,there exists some geodesic connecting them.

Fix anyk∈R.Given three pointsp,q,rin a geodesic spaceX,we can take a triangle △ink-planesuch that=|pq|,=|qr|and=|rp|.Ifk ＞0,we add the assumption that|pq|+|qr|+|rp|＜2π/.The triangleis unique up to a rigid motion. We call itcomparison triangle.Letdenote the angle at the vertexof the triangle △,and call it ak-comparison angle.

Definition 2.1Letk∈R.A geodesic spaceXis called anAlexandrov spacewith curvature≥kif it satisfies the following properties:

(1)It is locally compact;

(2)for any pointx∈X,there exists a neighborhoodUofxsuch that the following condition is satisfied:For any two geodesicsγ(t)⊂Uandσ(s)⊂Uwithγ(0)=σ(0):=p,thek-comparison angleκγ(t)pσ(s)is non-increasing with respect to each of the variablestands.

It is well known that the Hausdorffdimension of an Alexandrov space with curvature ≥k,for some constantk∈R,is always an integer(see,for example,[5]or[4]).LetXbe ann-dimensional Alexandrov space with curvature ≥k.We denote by vol then-dimensional Hausdorffmeasure onX.The Bishop inequality and the Bishop-Gromov inequality are satisfied onX(see[4]).In particular,the doubling condition is satisfied onX.

Lettingp∈X,given two geodesicsγ(t)andσ(s)withγ(0)=σ(0)=p,the angle

is well defined. We denote bythe set of equivalence classes of geodesicγ(t)withγ(0)=p,whereγ(t)is equivalent toσ(s)if ∠γ′(0)σ′(0)=0.The completion of metric spaceis called the space of directions atp,denoted by Σp. The tangent cone atp,Tp,is the Euclidean cone over Σp. For two tangent vectorsu,v∈Tp,their“scalar product”is defined by(see Section 1 in[34])

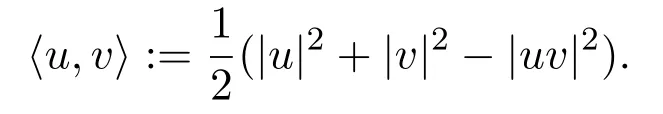
Definition 2.2[4]The boundary of an Alexandrov spaceXis defined inductively with respect to dimension. If the dimension ofXis one,thenXis a complete Riemannian manifold and theboundaryofXis defined as usual.Suppose that the dimension ofXisn≥2.A pointpis aboundary pointofXif Σphas non-empty boundary.

From now on,we always consider Alexandrov spaces without boundary.

For anyδ ＞0,we denote

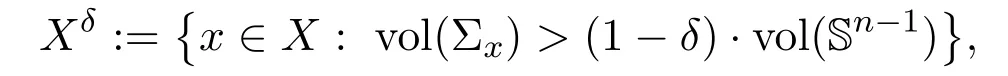
where Sn-1is the standard(n-1)-sphere,and vol denotes the(n-1)-dimensional Hausdroffmeasure.Xδis an open set(see[4]).The setSδ:=XXδis called theδ-singular set.Each pointp∈Sδis called aδ-singular point.The set

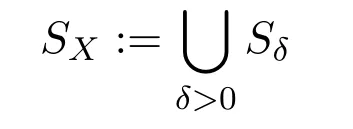
is called asingular set.A pointp∈Xis called asingular pointifp∈SX.Otherwise it is called aregular point. Equivalently,a pointpis regular if and only ifTpis isometric to Rn([4]). It is proved in[4]that the Hausdorffdimension ofSXis≤n-1.We remark that the singular setSXmight be dense inX([29]).

Some basic structures of Alexandrov spaces are in the following.

Proposition 2.1Let k∈Rand X be an n-dim Alexandrov space with curvature≥k.There exists a BVloc-Riemannian metric g on Xδsuch that

·the metric g is continuous in XSX([29,31]);

·the distance function on XSXinduced from g coincides with the original one of X([29]);

·the Riemannian measure on XSXinduced from g coincides with the Hausdorffmeasure of X([29]).

A pointpis called asmoothpoint if it is regular and there exists a coordinate system(U,φ)aroundpsuch that

where(gij)is the corresponding Riemannian metric in the above Proposition 2.1 nearpand(δij)is the identityn×nmatrix. It is shown in[31]that the set of smooth points has full measure.

2.2 The exponential map and second variation of arc-length

LetXbe ann-dimensional Alexandrov space andp∈X.For each pointx̸=p,the symboldenotes the direction atpcorresponding tosomegeodesicpx.Denote by

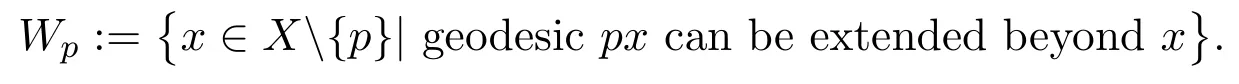
According to[29],the setWphas full measure inX.For eachx∈Wp,the directionis uniquely determined,since any geodesic inXdoes not branch([4]).Recall that the map logp:Wp→Tpis defined by logp(x):=|px|·(see[34]).It is one-to-one fromWpto its image

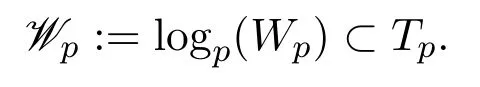
The inverse map of logp,

is called theexponential map at p.

One of the technical difficulties in Alexandrov geometry comes from the fact that Wpmay not contain any neighbourhood of the vertex of the coneTp.IfXhas curvature ≥konBp(R),then exponential map

is a non-expending map([4]),whereTk p is thek-cone over Σpandois the vertex ofTp.

In[32],A.Petrunin established the notion of parallel transportation and second variation of arc-length on Alexandrov spaces.

Proposition 2.2(Petrunin,Theorem 1.1.B in[32])Let k∈Rand X be an n-dimensional Alexandrov space with curvature≥k. Suppose that points p and q satisfy that the geodesic pq can be extended beyond both p and q.Then,for any fixed sequence{ϵj}j∈Ngoing to0,there exist an isometry T:Tp→Tqand a subsequence{εj}j∈N⊂{ϵj}j∈Nsuch that

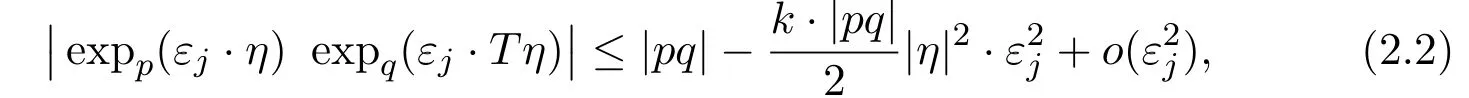
for any η∈Tpsuch that the left-hand side is well-defined.

Here and in the following,we denote byg(s)=o(sℓ)if the functiong(s)satisfies

The following asymptotic behavior ofWparound a smooth pointpwas proved in[39].

Lemma 2.1(Lemma 2.1 in[39])Let p∈X be a smooth point.We have

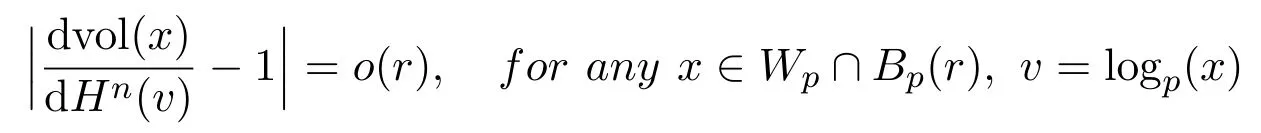
and

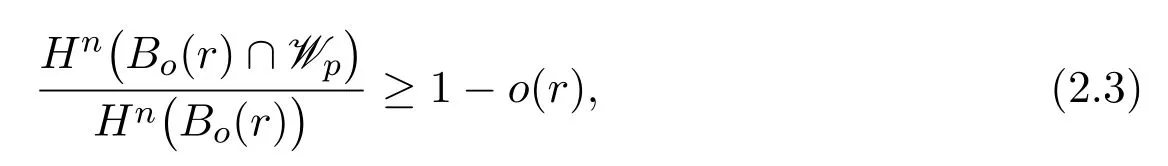
where Bo(r)⊂Tpand Hnis n-dimensional Hausdorffmeasure on Tp

2.3 Semi-concave functions and Perelman's concave functions

LetXbe an Alexandrov space without boundary and Ω ⊂Xbe an open set.A locally Lipschitz functionf:Ω →R is called to beλ-concave([34])if for all geodesicsγ(t)in Ω,the function

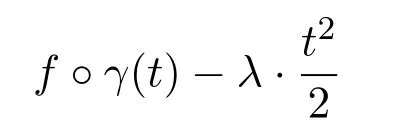
is concave.A functionf:Ω →R is called to besemi-concaveif for anyx∈ Ω,there exist a neighborhood ofUx∋xand a numberλx∈R such thatf|Uxisλx-concave(see Section 1 in[34]for the basic properties of semi-concave functions).

Proposition 2.3(Perelman's concave function,[19,30])Let p∈X.There exist a constant r1＞0and a function h:Bp(r1)→Rsatisfying:

(i)h is(-1)-concave;

(ii)h is2-Lipschitz,that is,h is Lipschitz continuous with a Lipschitz constant2.

We refer the reader to[39]for the further properties for Perelman's concave functions.

2.4 Sobolev spaces and Laplacian

Several different notions of Sobolev spaces have been established on metric spaces,see[6,13,23-25,36]1In[6,13,36],Sobolev spaces are defined on metric measure spaces supporting a doubling condition and a Poincar´e inequality..They coincide each other on Alexandrov spaces.

From now on,we assume thatXis ann-dim Alexandrov space with curvature≥k,Ω ⊂Xis a domain ofX. It is well-known that the metric measure space(X,|·,·|,vol)supports a local(weak)Poincar´e inequality.

We denote by Liploc(Ω)the set of locally Lipschitz continuous functions on Ω,and by Lipc(Ω)the set of Lipschitz continuous functions on Ω with compact support.

For a continuous functionu:XR,define

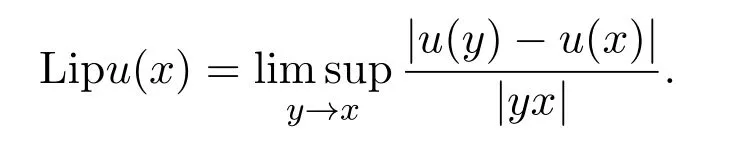
Definition 2.3For any 1 ≤p≤+∞ andu∈Liploc(Ω),itsW1,p(Ω)-norm is defined by

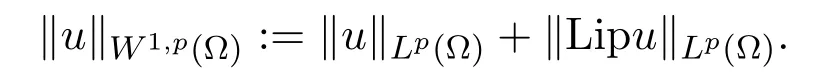
Sobolev spacesW1,p(Ω)is defined by the closure of the set

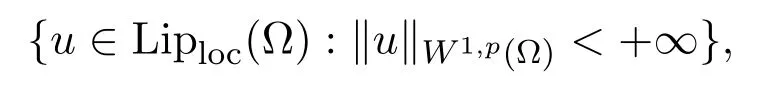
underW1,p(Ω)-norm. Spacesis defined by the closure of Lipc(Ω)underW1,p(Ω)-norm.We denote byW1,pc (Ω)={f∈(Ω):fhas compact support}.We say that a functionf∈iff∈W1,p(Ω′)for every open subset Ω′⊂⊂ Ω.

Cheeger[6,Theorem 4.48]proved thatW1,p(Ω)is reflexive when 1＜p ＜∞.We denote by ∇uthe weak gradient ofu∈W1,p(Ω).

We recall the chain derivation property ofW1,2(Ω).It is formulated as follows:Forf,g∈W1,2(Ω)∩L∞(Ω)and Φ:R →R which isC1on the range off,Φ(f)belongs toW1,2(Ω)and

Givenf∈,the Laplacian offis defined as a functional on Lipc(Ω)by

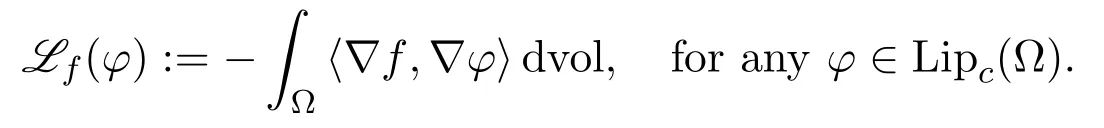
Givenh∈,a functionf∈is said to satisfy the inequality

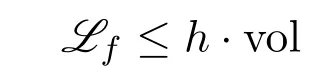
in the sense of distribution if the inequality

holds for all 0 ≤φ∈Lipc(Ω). In this case,the functional Lfis a signed Radon measure.

Given a functionh∈L2(Ω)andg∈W1,2(Ω),we can solve the Dirichlet problem of the equation

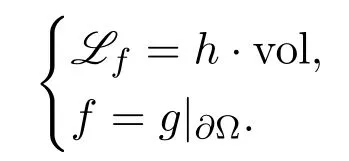
Indeed,by Sobolev compact embedding theorem(see[12,24])and a standard argument(see,for example,[10]),it is known that the solution of the Dirichlet problem exists uniquely inW1,2(Ω)(see,for example,[6,Theorem 7.12 and Theorem 7.14]).Furthermore,if we add the assumptionh∈Lswiths ＞n/2,then the solutionfis locally H¨older continuous in Ω(see[21,24]).

Lemma 2.2(Corollary 5.8 in[39],[14])LetΩbe a bounded domain of an Alexandrov space. Assume that g∈L∞(Ω). If f∈W1,2(Ω)is a weak solution of the Poisson equation

Then f is locally Lipschitz continuous inΩ.

We need the following mean value inequality.

Proposition 2.4([40],Proposition 3.2)Let X be an n-dimensional Alexandrovspace andΩbe a bounded domain in X. Assume a function h∈withh(x)≤C for some constant C. Suppose that f∈∩C(Ω)is nonnegativeand satisfies that

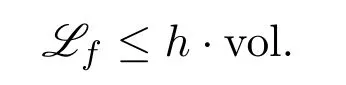
If p∈ Ωis a Lebesgue point of h,then

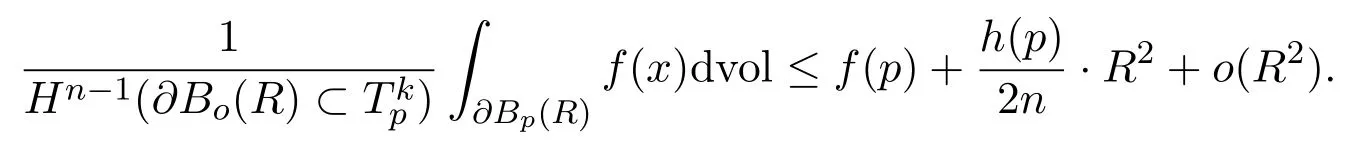
The following lemma is due to Kinnunen-Martio[20],see also[40].

Lemma 2.3LetΩbe a bounded domain of an Alexandrov space.Assume thatf∈∩C(Ω)and g∈L∞(Ω).Then the following properties are equivalentto each other:

(i)f is a super-solution ofLf=g·volonΩ;

(ii)f satisfies the following comparison principle:For each domainΩ′⊂⊂ Ω,we have v≤f inΩ′,where v∈W1,2(Ω′)is the(unique)solution of

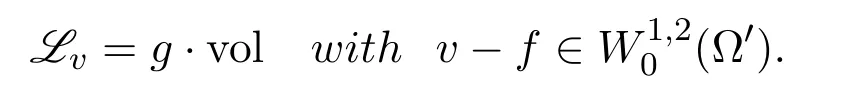
2.5 The heat equations

Given a domainG⊂Xand an intervalI=(a,b),Q=G×Iis called aparabolic cylinderin space-timeX×R.

For a parabolic cylinderQ,we equip with the product measure

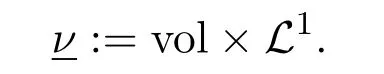
WhenG=Bx0(r)andI=Iλ0(r2):=(λ0-r2,λ0+r2),we denote by the cylinder

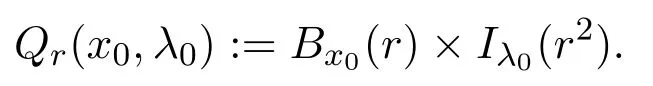
If without confusion arises,we shall write it asQr.

Definition 2.4LetQ=G×Ibe a cylinder.A functiong(x,λ)∈is said a(weak)super-solutionof the heat equation

if it satisfies

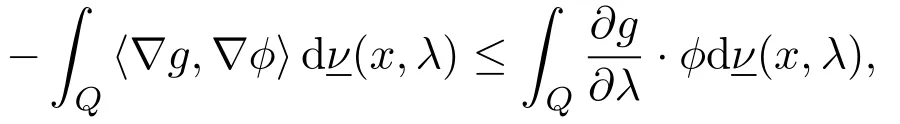
for all nonnegative functionφ∈Lipc(Q).

A functiong(x,λ)is said asub-solutionof equation(2.4)onQif-g(x,λ)is a super-solution onQ.A functiong(x,λ)is said alocal weak solutionof equation(2.4)onQif it is both a sub-solution and a super-solution onQ.

The theory forlocal weak solutionof the heat equation on metric spaces has been developed by Sturm in[37]and,recently,by Kinnunen-Masson[22],Marola-Masson[28].They proved the following weak Harnack inequality for sub-solutions of the heat equation(See[37,Theorem 2.1]or[28,Lemma 4.2]).

Lemma 2.4[37,28]Let G×I be a papabolic cylinder in X×R,and g(x,λ)be anonnegative,local bounded sub-solution of the heat equationon Qr⊂G×I.Then there exists a constant C=C(n,k,diamG),depending only on n,k anddiamG,such that we have

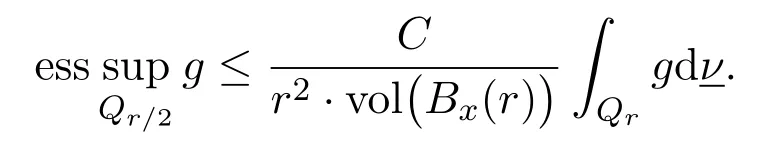
For a function,An equivalent characterization for solutions inof the heat equation is given in the following lemma.

Lemma 2.5([40],Lemma 6.12)Let Q=G×I be a cylinder. Suppose afunction g(x,λ)∈.If,for almost all λ∈I,the function xg(x,λ)is asuper-solution of the Poisson equation

Then g(x,λ)is a super-solution of the heat equation

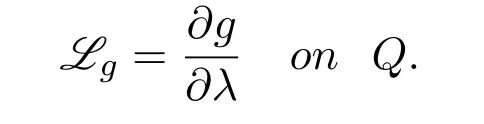
2.6 Energy functional and Sobolev spaces into metric space

From now on,we assume that Ω is a domain of an Alexandrov space and that(Y,dY)is a complete metric space. Fix anyp∈[1,∞). Fixed a pointP∈Y,a Borel measurable mapu: Ω →Yis said to be in the spaceLp(Ω,Y,P)if it has separable range and

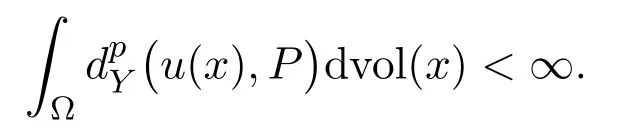
If vol(Ω)＜∞,the spaceLp(Ω,Y,P)does not depend on the choice of the pointP∈Y.In this case,we denoteLp(Ω,Y)the space.The spaceLp(Ω,Y)is a metric space under the distance

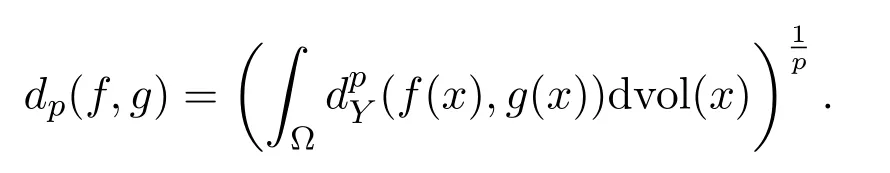
The space(Lp(Ω,Y),dp)forms a complete metric space.

Definition 2.5Foru∈Lp(Ω,Y),the approximating energyis defined by

for anyφ∈Cc(Ω),where the approximating density ofuis defined by with the constantcn,p=andσbeing the canonical volume on.

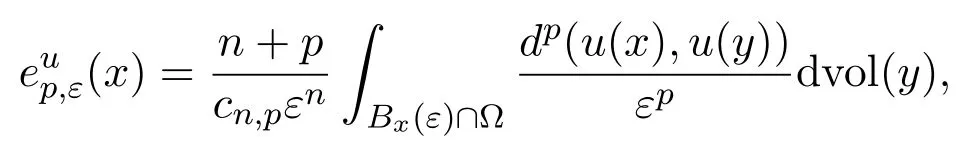
When Ω is a domain of a smooth manifold,and(Y,d)is an arbitrary metric space,Korevaar-Schoen[23]proved that,for anyφ∈Cc(Ω),the limit

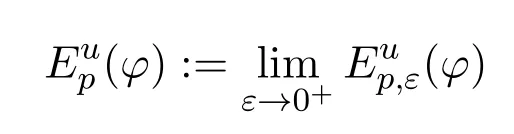
exists.This is extended to the case where Ω is a domain of a Lipschitz manifold[11],or a domain of a polyhedra[7],or Ω is a domain of an Alexandrov space with curvature bounded below[25].We calltheenergy functionalofu,defined onCc(Ω).

Definition 2.6We define the Sobolev space from Ω toYby

Notice that the space of Lipschitz maps Lip(Ω,Y)⊂W1,p(Ω,Y). However,in general,this imbedding does not dense.

Proposition 2.5[25]Let1＜p ＜∞and u∈W1,p(Ω,Y).Then the following assertions(1)-(3)hold.

(1)(Energy measure,[25,Theorem 4.1 and Proposition 5.1])There exists a finiteBorel measure,denoted byagain,onΩ,is calledenergy measureof u,such thatfor any0 ≤φ∈Cc(Ω),

Furthermore,the measure is strongly local.That is,for any nonempty open subset O⊂ Ω,we have u|O∈W1,p(O,Y),and moreover,if u is a constant map almosteverywhere on O,then(O)=0.

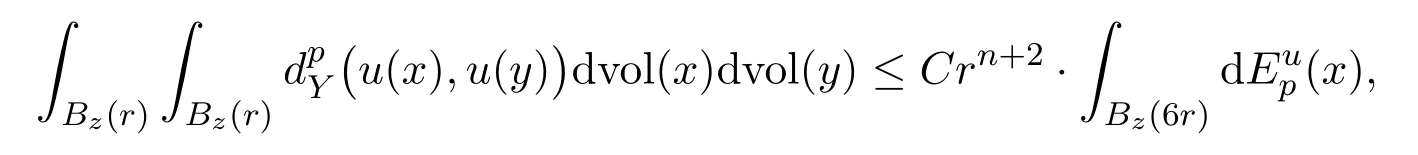
where the constant C given in[25,page 61]depends only on the constants R,ϑ,andΘin the Definition2.1for WMCPBG condition in[25].In particular,for the case of Alexandrov spaces as shown in the proof of Theorem2.1in[25],one can choose R ＞0arbitrarily,ϑ=1and

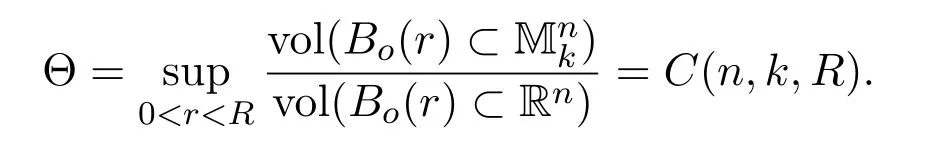
(3)(Equivalence forY=R,[25,Theorem 6.2])If Y=R,the above Sobolev space W1,p(Ω,R)is equivalent to the Sobolev space W1,p(Ω)given in Definition2.3.Precisely,for any u∈W1,p(Ω,R),the energy measureis absolutely continuous with respect tovoland

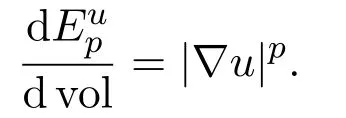
Given 1＜p ＜∞andu∈W1,p(Ω,Y). As a Radon measure on Ω,according to the Lebesgue's decomposition theorem(see,for example,[8,Section 1.6]),the energy measurecan be written as

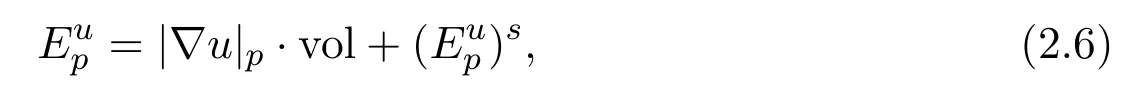
for some|∇u|p∈L1(Ω,dvol),and a Borel measurewhich is the singular part of.Here and in the rest of this paper,the function|∇u|palways denotes the absolutely continuous part of.

Let recall the following mean value property forW1,p(Ω,Y)-maps.

Lemma 2.6([40]Corollary 4.6)Let1＜p ＜∞and u∈W1,p(Ω,Y).Then,forany sequence of positive numberconverging to0,there exists a subsequence{εj}j⊂{ϵj}jsuch that for almost everywhere x0∈ Ω,we have the following mean value property:

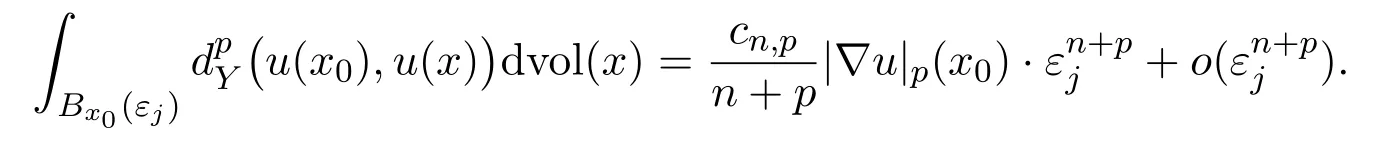
2.7 Spaces of curvature bounded from above

Definition 2.7(see,for example,[5]) A geodesic space(Y,dY)is called to be withcurvature bounded from abovebyl(in the sense of Alexandrov),if the following comparison property holds:Given any triangle △PQR⊂Yand pointS∈QRwith

there exist a comparison triangleand a pointwith

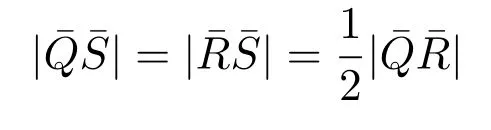
such that

It is also called aCAT(l)space.We write alsoCAT(0)byNPC.

Given aCAT(l)spaceYandp∈Y,the space of directions ofYatpis welldefined.For each pointx̸=p,the symbolalso denotes the direction atpcorresponding toone ofgeodesicpx.We refer the readers to[5]for the details.

Definition 2.8Given any pair of pointsP,Qin aNPCspace andλ∈[0,1],one defines(1-λ)P+λQto be a point on a unique geodesic joiningPandQthat is a fractionλaway fromP,that is

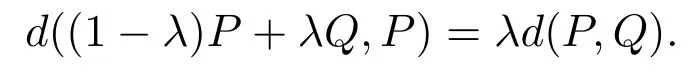
Some convexity arguments of the distance function on aNPCspace is given in the following.

Lemma 2.7[35]Let△PQS be a triangle in a CAT(0)space. For a pair of numbers0 ≤η,η′≤1,define Pη′=(1-η′)P+η′Q and Sη=(1-η)S+ηQ.Then

The following lemma is a special case of Corollary 2.1.3 in[23].

Lemma 2.8Let(Y,dY)be a CAT(0)space.Take any ordered sequence{P,Q,R,S}⊂Y,and let point Qmbe the mid-point of QR.We denote the distance dY(A,B)abbreviatedly by dAB.Then we have

Definition 2.9Given a geodesic space(Z,dZ)with diam(Z)≤π,the Euclidean cone overZ,denoted byC(Z),is defined by

where two points[P,t]～[Q,s]if and only if thatt=s=0 or thatP=Qandt=s.The equivalence class[P,0]is the vertex ofC(Z),denoted byo.The coneC(Z)can be made into a metric space with the distanceDdefined by the cosine law

It is well-known that the Euclidean cone over aCAT(1)space is aCAT(0)space(see,for example[5]).

3 The Ginzburg-Landau Functional

We continue to assume that Ω is a bounded domain of an Alexandrov space.LetY=C(Z)be the Euclidean cone over a complete locally compact geodesic spaceZ,with curvature(Z)≤1.We denote byothe vertex ofY.In this section,we will prove some properties for the minimizers of the Ginzburg-Landau functional.

Recall the Ginzburg-Landau functionalIK(·):W1,2(Ω,Y),

where,and in the sequel,we always denote by|u|:=dY(o,u).

Definition 3.1We say thatu∈W1,2(Ω,Y)is a minimizer of(3.1)ifIK(u)≤IK(v)for everyv∈W1,2(Ω,Y)withdY(u,v)∈(Ω).

Forv∈W1,2(Ω,Y),we say thatvsatisfies|v|≤1 on∂Ω,if(|v|-1)+∈.Herea+:=max{a,0}.

Lemma 3.1(weak maximum principle,[35])Let u∈W1,2(Ω,Y)be a minimizer of(3.1).If|u|≤1on ∂Ω,then we have|u|≤1almost everywhere onΩ.

ProofLetB={y∈Y=C(Z):|y|≤1}.Let Π be the canonical projection fromYontoB,namely,it sends(y,t)to(y,min{t,1}).Obviously,Π is a 1-Lip map(that isdY≤dY(u,v)for anyu,v),so we have

On the other hand,note that|u|≤1 on∂Ω,by the definition of Π,we have

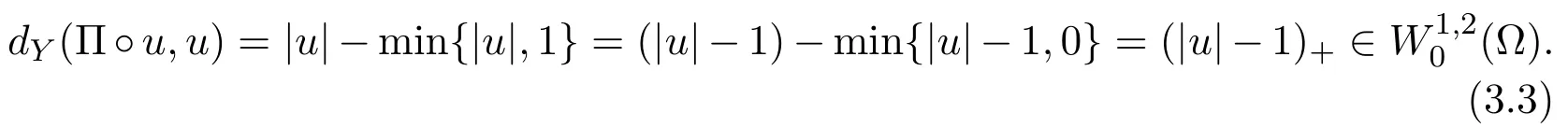
Note thatuis a minimizer of(3.1),by(3.3),we have

Thus,the combination of(3.2)and(3.4)implies that

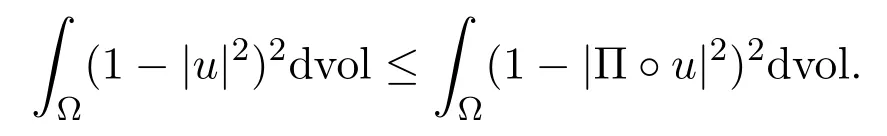
This inequality implies that|u|≤1 almost everywhere on Ω.The proof is completed.

Lemma 3.2Suppose that u∈W1,2(Ω,Y)is a minimizer of(3.1)with|u|≤1on ∂Ω.For every fixed P∈Y,the function

satisfies

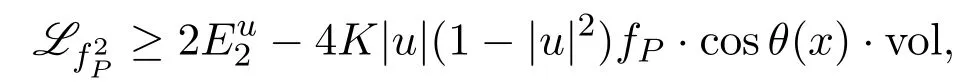
where θ(x)=is the angle such that

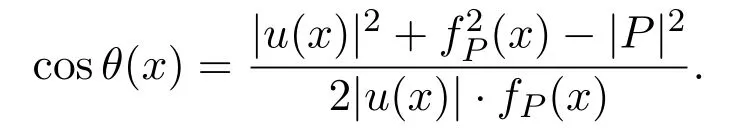
In particular,we have

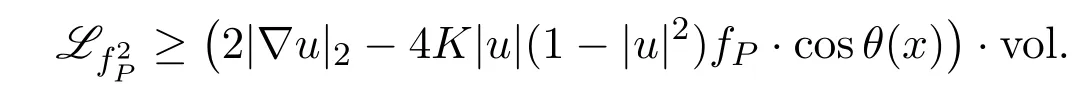
ProofDue to Lemma 3.1,we know that|u|≤1.For anyφ∈Lipc(Ω),0 ≤φ≤1,letuφ=(1-φ)u+φP.Applying Lemma 2.7,we obtain that

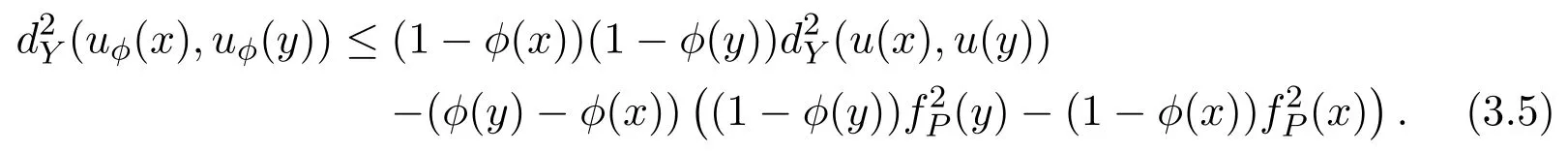
Thus,we have,for anyη∈Cc(Ω),0 ≤η≤1,

Lettingε→0,we have

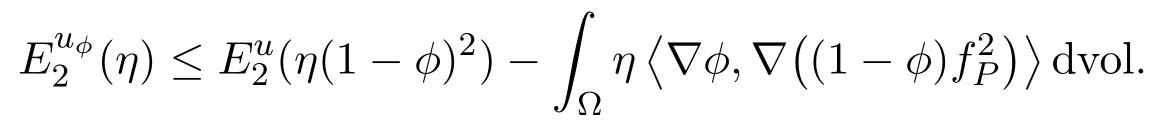
Lettingη↗1,we get that

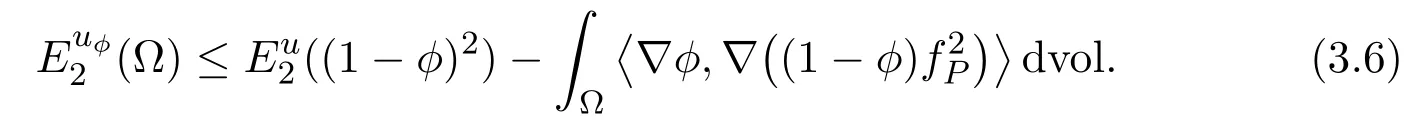
Note thatφ∈Lipc(Ω),thendY(uφ,u)∈W1,20 (Ω).Recall thatuis a minimizer of(1.2).Thus,we have

The combination of(3.6)and(3.7)implies that

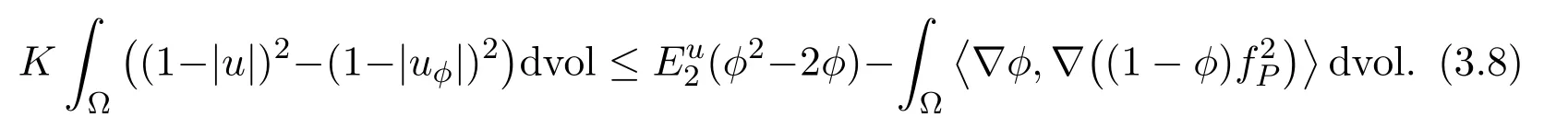
For anyt∈(0,1),by replacingφwithtφin(3.8),and divington both sides of(3.8),we obtain

On the other hand,by the definition of distance in cones(the cosine law),we have

Thus,lettingt→0 in(3.9),and noticing that|utφ|-|u|/t≤dY(u,utφ)/t=φfP(≤|P|+1),the dominated convergence theorem and(3.9)conclude that

The proof is completed.

Corollary 3.1Let u,P and fPbe as in Lemma3.2.Then we have

whereProofDue to Lemma 3.1,we know that|u|≤1.Forε ＞0 sufficiently small,defineBy Lemma 3.2,for any 0 ≤φ∈(Ω)∩L∞(Ω),we have

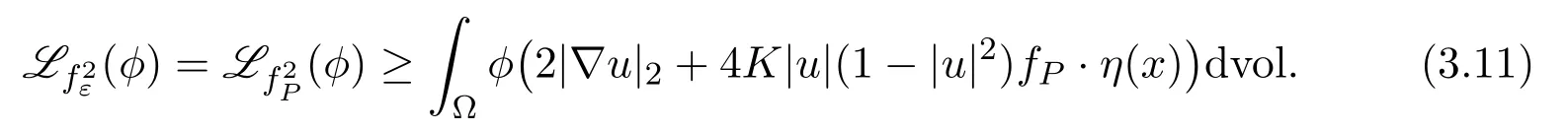
On the other hand,

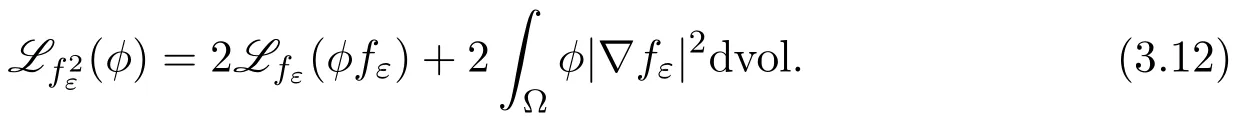
Note that|∇u|2≥|∇fP|2＞|∇fε|2.The combination of(3.11)and(3.12)implies

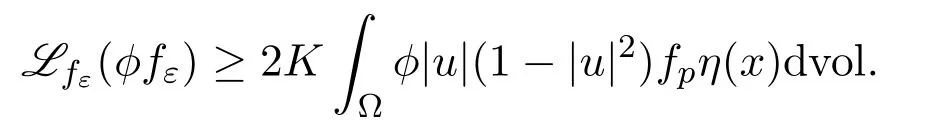
Noticing thatfε≥ε. Thus,by replacingφ/fεin the above inequality,we obtain that

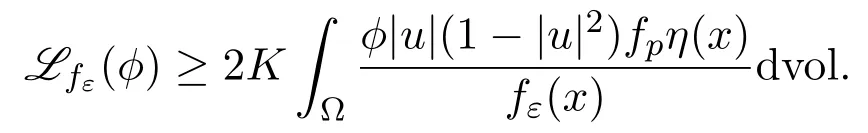
Recall thatW1,2(Ω)is reflective.It is easy to see thatfεis uniformly bounded inW1,2(Ω).Finally,by taking a subsequence of{εj}converging to 0,and applying the dominated convergence theorem to the right hand side of the above inequality,we conclude that

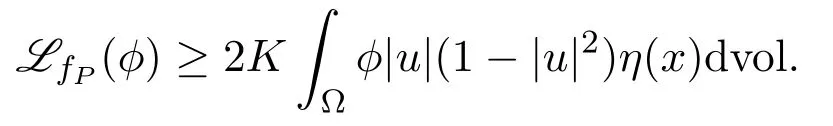
This completes the proof.

The Lemma 3.2 and Corollary 3.1 play the same role of the subharmonicity ofdY(P,v(x))for harmonic mapsv(x). It has two main consequences: the locally H¨older continuity ofuand an estimate for pointwise Lipschitz constant ofu,

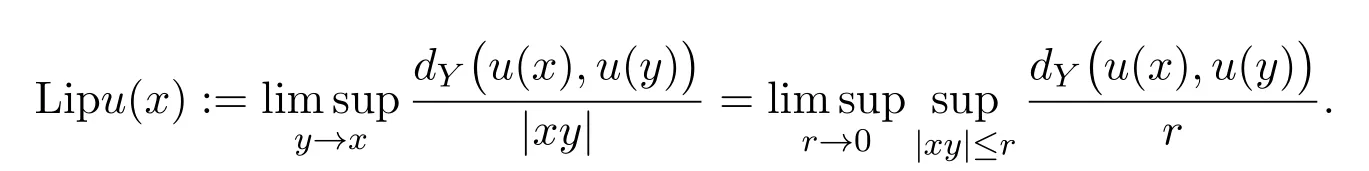
We will discuss these properties in the following section.

Let Ω be a bounded domain in ann-dimensional Alexandrov space(X,|·,·|)with curvature ≥kfor somek≤0. We continue to assume thatY=C(Z)is the Euclidean cone over a complete locally compact geodesic spaceZ,with curvature(Z)≤1.ois the vertex ofY. Throughout this section,we suppose thatuis a minimizer of(3.1)with|u|≤1 on∂Ω.According to Lemma 3.1,we have|u|≤1.

4.1 H¨older continuity for the minimizer u

Notice that Ω satisfies the volume doubling property and measure vol supports aL2-Poincare inequality.By employing a same method in[17]and Lemma 3.2,one can obtain the local H¨older continuity ofu.This method was also used in[9].

Our considerations are essentially local,in some ballBx0(12R)⊂⊂ Ω with 12R ＜1.We denote byB(r):=Bx0(r).

Theorem 4.1LetΩbe a bounded domain in an n-dimensional Alexandrov space(X,|·,·|)with curvature≥k for some k≤0.Y=C(Z)is the Euclidean cone over a complete locally compact geodesic space Z,with curvature(Z)≤1.o is the vertex of Y.Suppose that u is a minimizer for(3.1)with|u|≤1on ∂Ω.Then u is locally H¨older continuous onΩ.

The argument of Theorem 4.1 is almost parallel with Jost's proof for harmonic maps in[17].

For a functionv∈L∞,we put

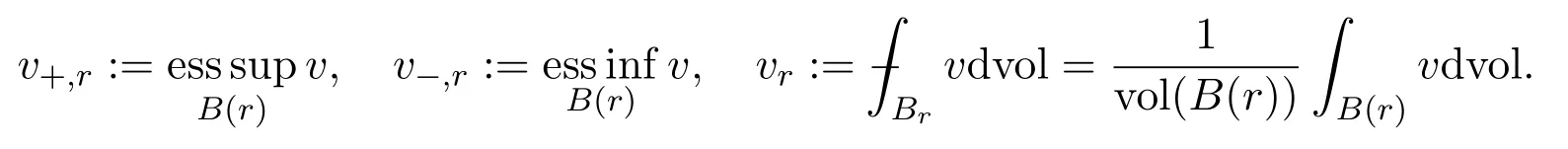
To prove of Theorem 4.1,we need some lemmas.

Lemma 4.1Suppose that u is a minimizer for(3.1)with|u|≤1.Let P∈Ywith|P|≤1,fP(x):=dY(u(x),P),v=. Then there exist constants δ0=δ0(n,k,R)∈(0,1)and C1＞0,independent of v and r,such that

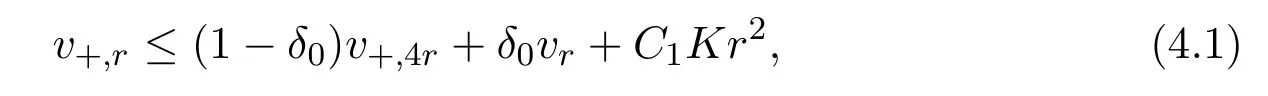
for r ＜R.Here and in the sequel of this section,c1,c2,···,C1,C2,···,denote the constants depending only on n,k,R.

ProofLetz:=v+,4r-v.Then by Lemma 3.2,we have

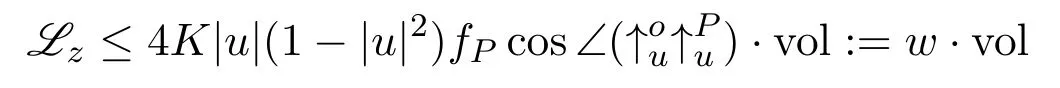
in the sense of distribution.From the classical Nash-Moser iteration(see,for example,Theorem 8.17 in[10]),we conclude,for anyq ＞n,that there exists a constantC(n,k,R,q)＞0 such that

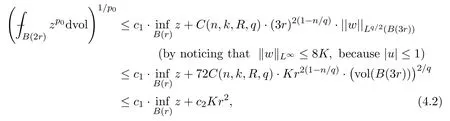
for some constantsc1,c2＞0 andp0＞1,where we have used the Bishop inequality

On the other hand,by the volume doubling property,we have

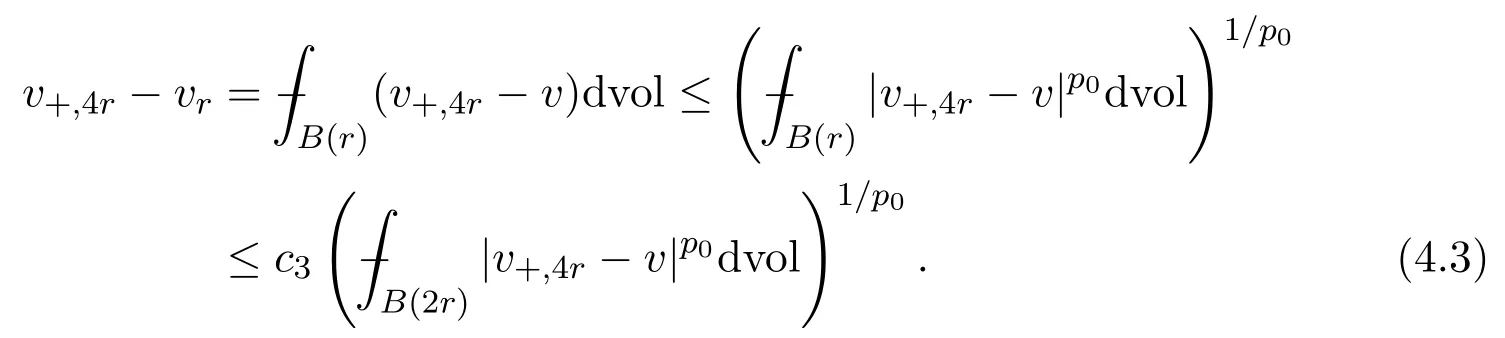
The combination of(4.2)and(4.3)implies that

Thus,we have

This completes the proof.

Letvandδ0be as in Lemma 4.1,and suppose 0＜ ε ＜1/4. By using the same iterating method in[17,Lemma 7],one can get that there exist anm∈N(independent ofvandε)and a constantC(n,k,R,ε)such that

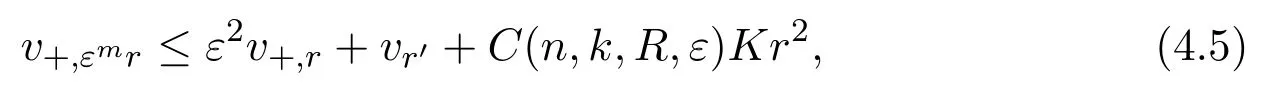
for somer′withεmr≤r′≤r/4(r′may depend onvandε). We only need to replace the first inequality of the proof of[17,Lemma 7]by

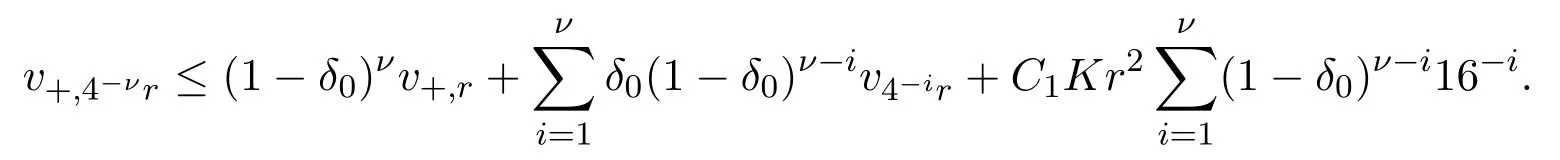
By using the same argument of[17,Lemma 8],one can obtain the following lemma.

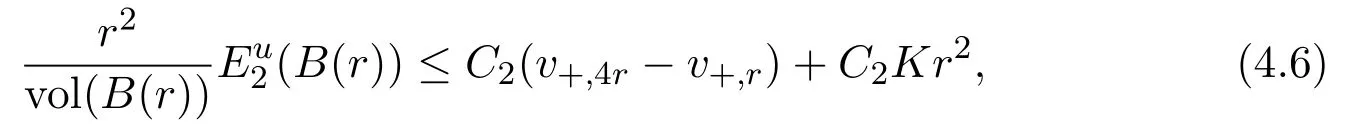
for some constant C2＞0.

ProofLetGbe the mollified Green function onB(r)relative toB(2r),then we have

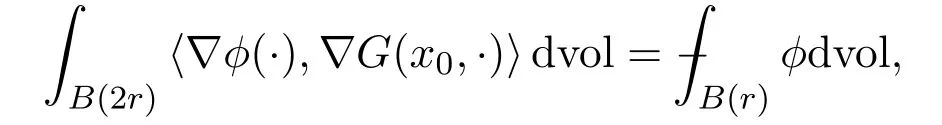
Lemma 4.2Let v be defined in Lemma4.1.Then we have

for allφ∈(B(2r)).Let

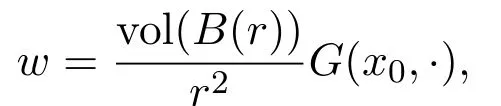
then we have

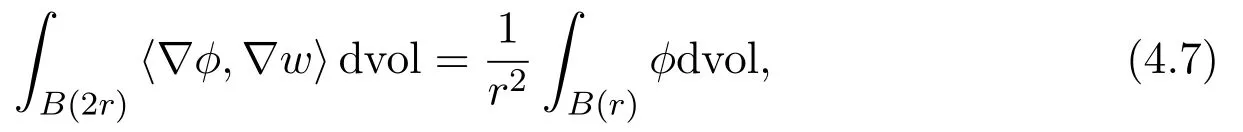
for allφ∈(B(2r)).More,we have from[3]that

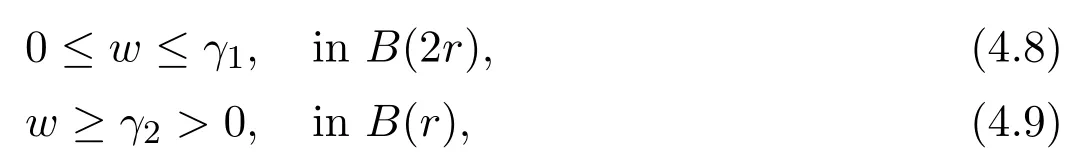
for constantsγ1,γ2.By replacing Lv≥for harmonic maps in[17,Lemma 8]and by Lemma 3.2 here,that is,

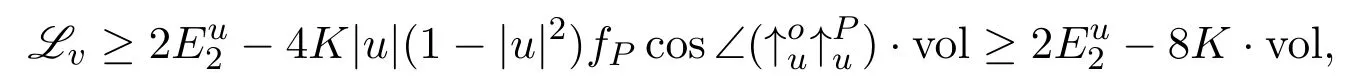
in the sense of distribution,and puttingz:=v-v+,4r,we have

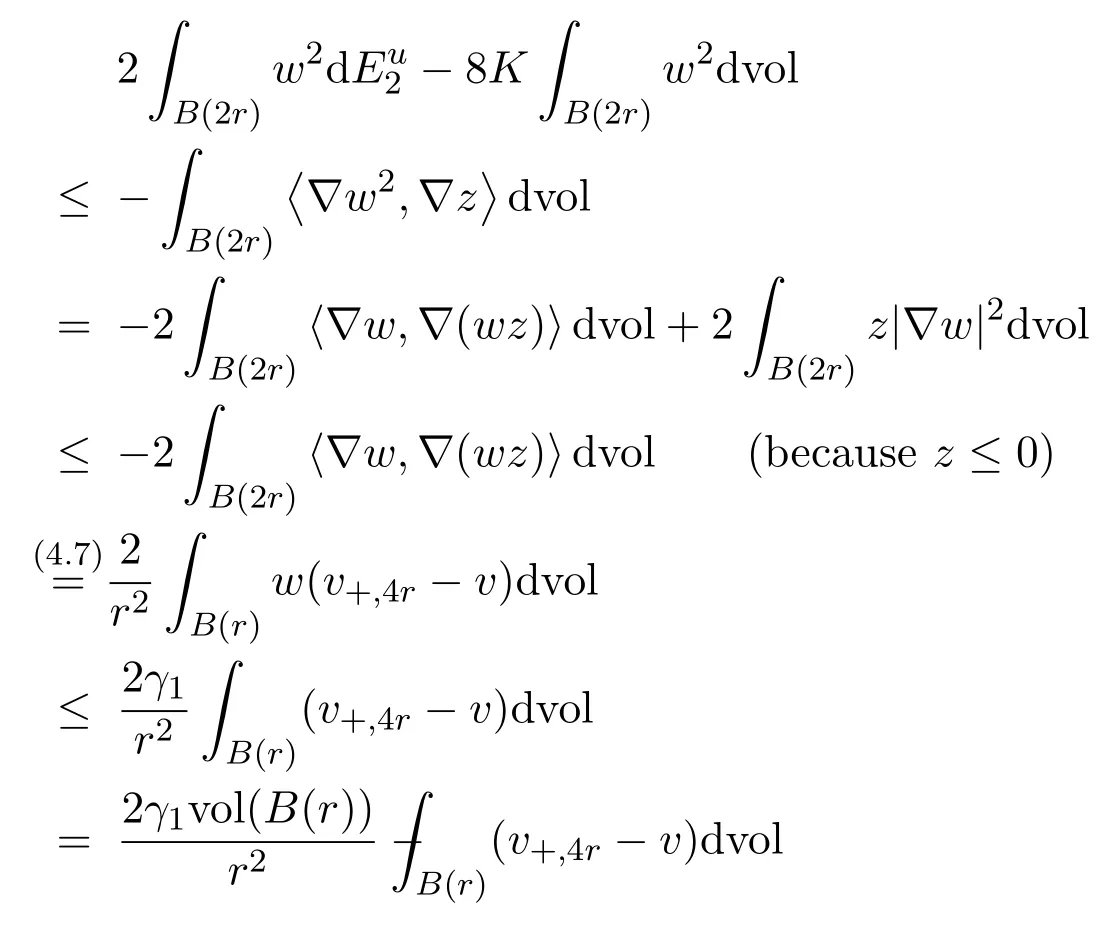
Hence,we obtain from(4.10)that

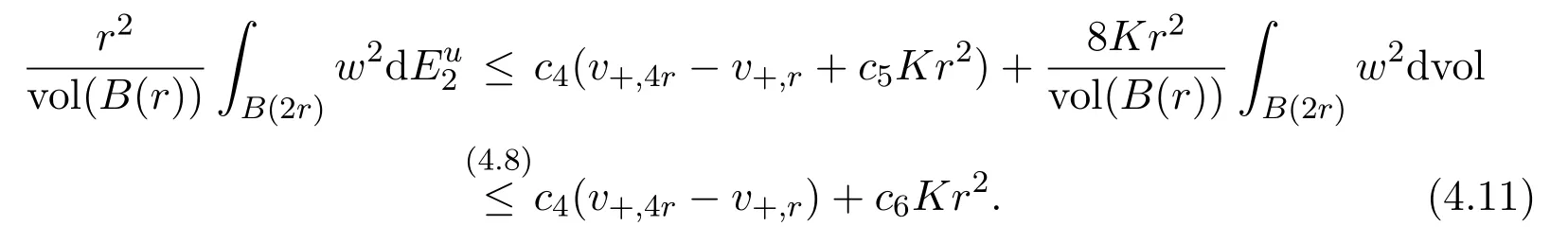
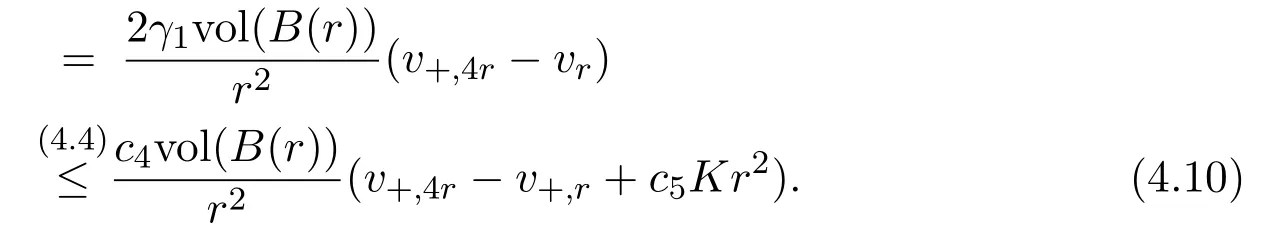
On the other hand,by(4.9),we get

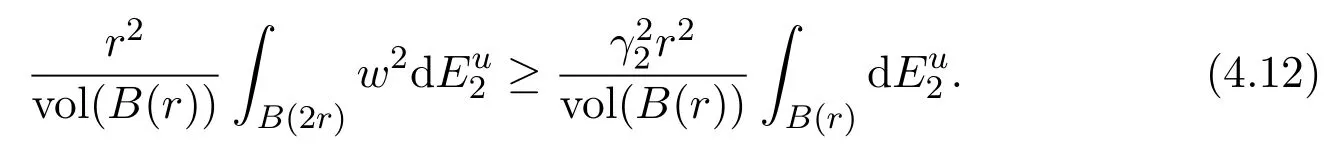
Thus,this lemma follows from the combination of(4.11)and(4.12).The proof is completed.

We are now in position to prove Theorem 4.1.

Proof of Theorem 4.1Due to Lemma 3.1,we know that|u|≤1.For|P|≤1,letfP:=dY(u(x),P)andv=.In the proof,we denote by

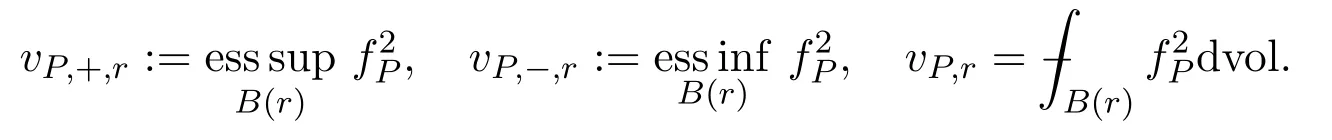
Applying(4.5)to the function(u,),withε=1/8.Recallr′,m∈N in(4.5).We have from by the Poincare inequality,Proposition 2.6(2),

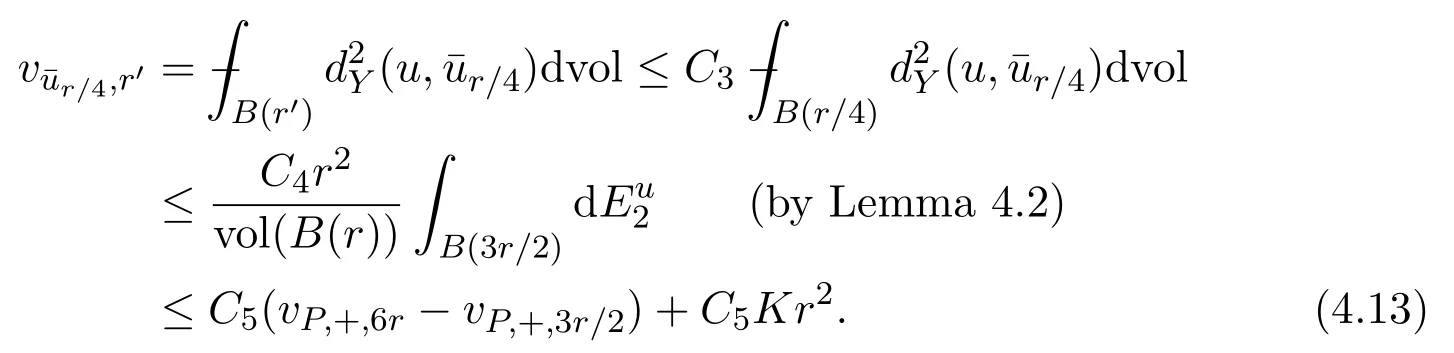
On the other hand,for allPin the convex hull ofu(B(εm)),by using(4.5),we have

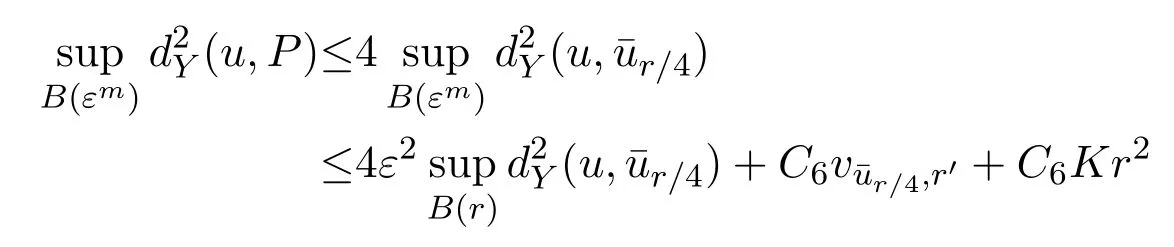
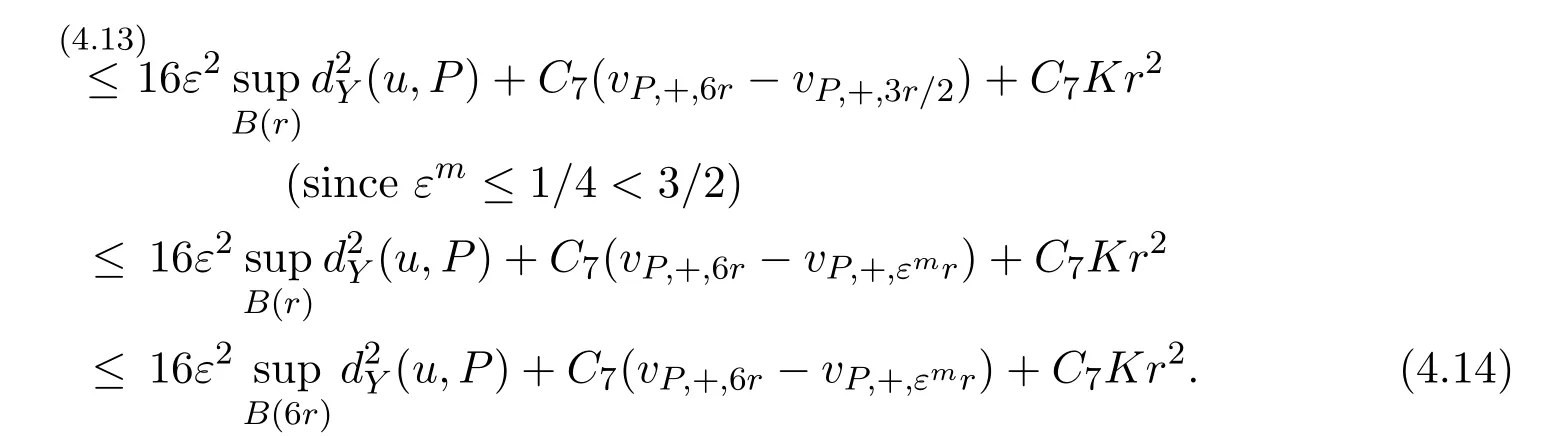
Now we letωP(ρ)=We obtain from(4.14)that

sincer ＜1.By iteration,we get

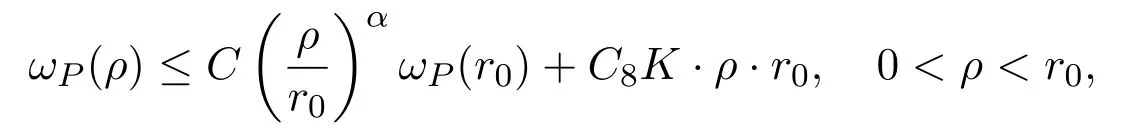
for allPin the convex hull ofu(B(ρ))and someα∈(0,1).TakeP=.Finally,by

we conclude thatuis locally H¨older continuous.The proof is completed.

4.2 Estimates for pointwise Lipschitz constant

Letube a minimizer of(3.1)with|u|≤1 on∂Ω from Ω of an Alexandrov space(X,|·,·|)to(Y,dY).According to Theorem 4.1 and Lemma 3.1,we know thatuis continuous in Ω and|u|≤1.

In this subsection,we will estimate thepointwise Lipchitz constantofu,that is,

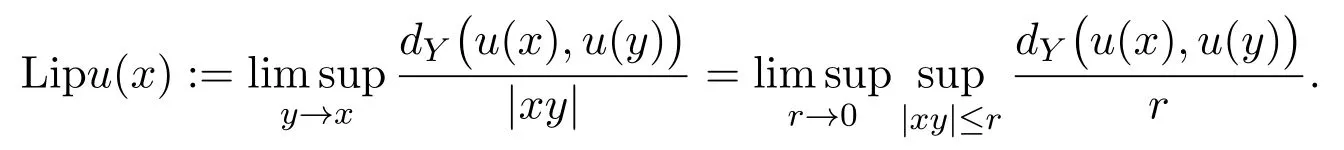
It is convenient to consider the functionf:Ω×Ω →R defined by

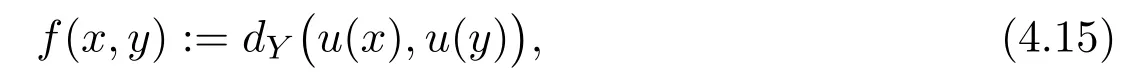
where Ω×Ω ⊂X×X,which is equipped with the product metric defined as

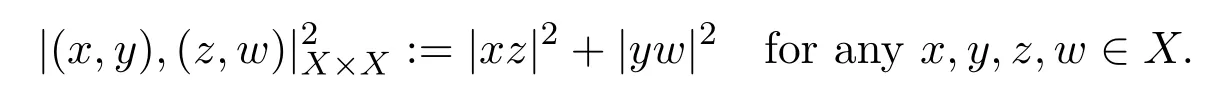
Recall that(X×X,|·,·|X×X)is also an Alexandrov space. The geodesic balls inX×Xare denoted by

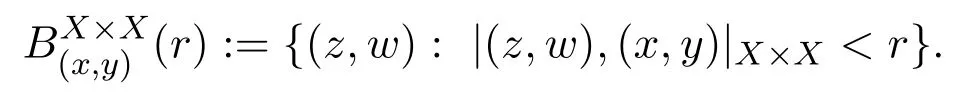
Proposition 4.1LetΩ,Y and u,f be as the above.Then

in the sense of distribution onΩ×Ω(Since X×X is also an Alexandrov space,thenotationmake sense).

ProofFor anyg∈W1,2(Ω × Ω),by Fubini's theorem,we can conclude that,for almost allx∈ Ω,the functionsgx(·):=g(x,·)are inW1,2(Ω),and that the same assertions hold for the functionsgy(·):=g(·,y). We denote by ∇X×Xgthe weak gradient ofg.Note that the metric onX×Xis the product metric,we have

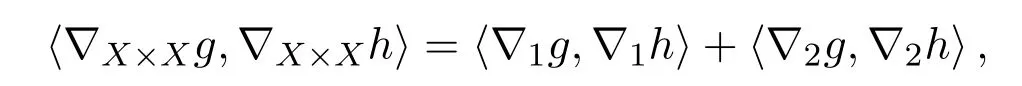
for anyg,h∈W1,2(Ω × Ω),where ∇1gis the weak gradient of the functiongy(·):=g(·,y):Ω →R,and ∇2gis similar.

Now,we are in the position to prove of(4.16).Take any test functionφ(x,y)∈Lipc(Ω×Ω)withφ(x,y)≥0,

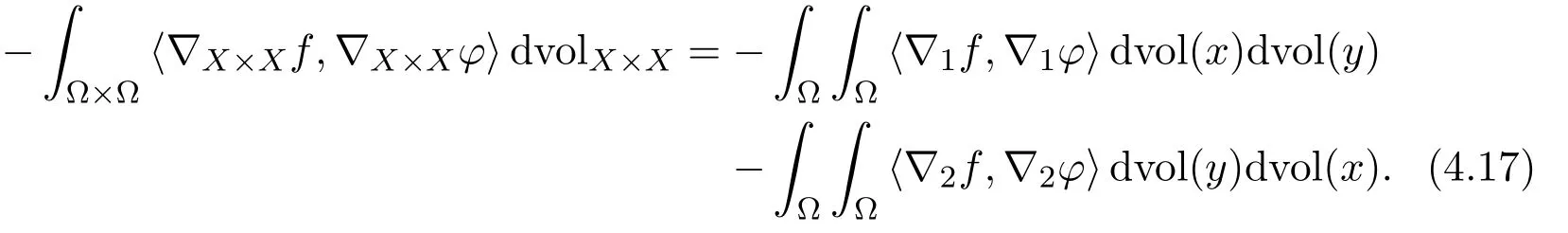
Define

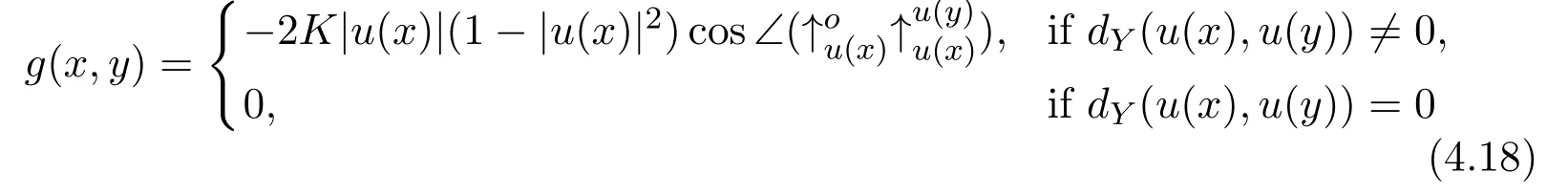
and

On the other hand,for any fixedy∈ Ω,note that the functionφy(·):=φ(·,y)∈Lipc(Ω).According to Corollary 3.1,we have,for any fixedy∈ Ω,

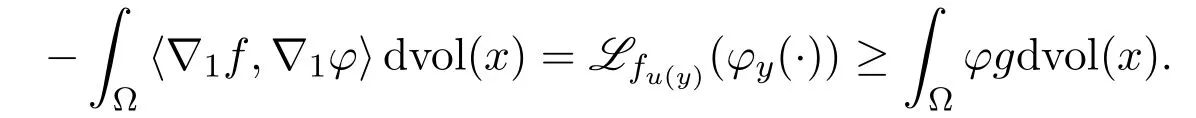
By the same argument,we get for any fixedx∈ Ω,

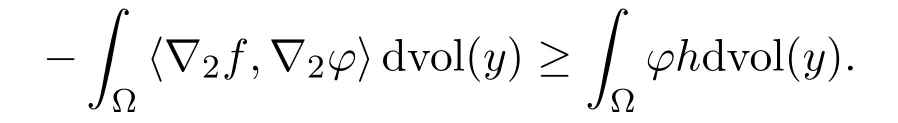
By substituting these above two inequalities into equation(4.17),we have

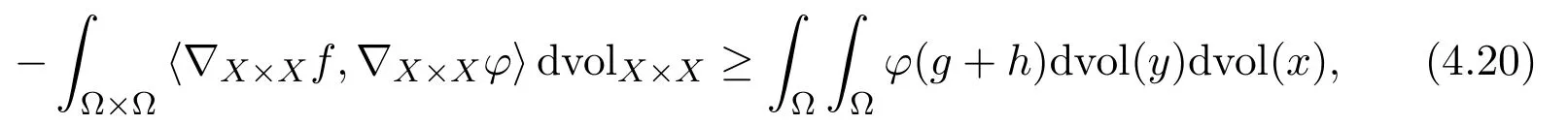
for any function 0 ≤φ∈Lipc(Ω × Ω).

We now give a lower bound of the functiong+h.We denotea=|u(x)|,b=|u(y)|,c=dY(u(x),u(y)),andθ1=Recall thatYis the Euclidian cone over a geodesic spaceZ,with curvature(Z)≤1,hence,whendY(u(x),u(y))̸=0,by the definition of the Euclidean cone(the cosine law for the distance ofY),we have

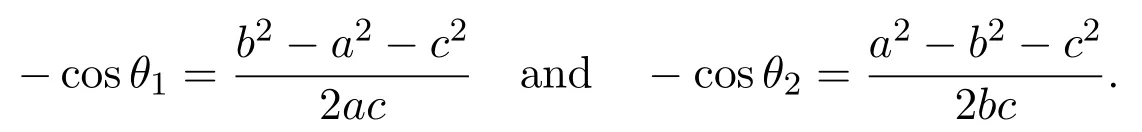
By direct computation,we have,whendY(u(x),u(y))̸=0,

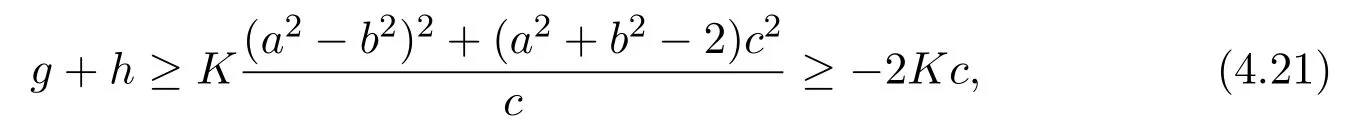
that is,

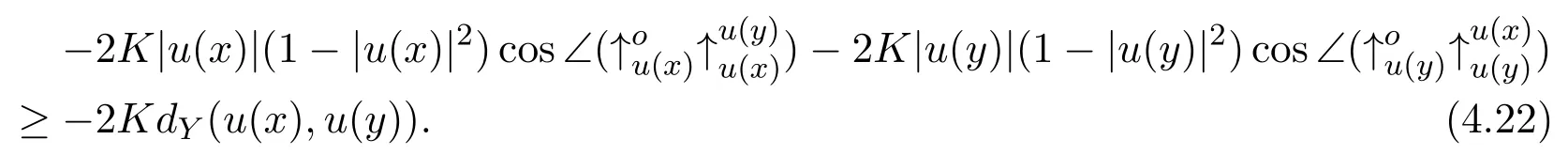
Thus,(4.16)follows from(4.20)and(4.21).The proof is completed.

Similar as in[40],we have the following estimates for pointwise Lipschitz constants of minimizers for(3.1).

Corollary 4.1LetΩbe a bounded domain in an n-dimensional Alexandrov space(X,|·,·|)with curvature≥k for some k≤0.The target space Y=C(Z)is the Euclidean cone over a complete locally compact geodesic space Z,with curvature(Z)≤1.o is the vertex of Y.Suppose that u is a minimizer for(3.1)with|u|≤1on ∂Ω.Then we have,for any ball Bq(R)⊂⊂Ω,there exists a constant C(n,k,R),depending only on n,k and R,such that

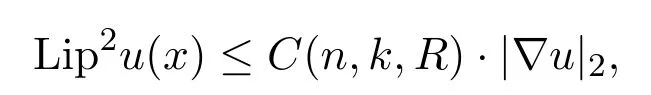
for almost everywhere x∈Bq(R/6).

ProofThe argument is the same as the proof of Theorem 5.5 in[40],by replacing the inequality≥0 can deduce the inequality

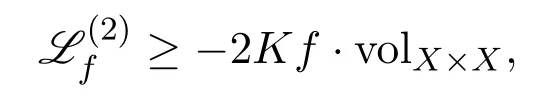
wheref(x,y):=dY(u(x),u(y)).The proof is completed.

Proposition 4.1 implies the following mean value inequality.

Lemma 4.3Suppose that u∈W1,2(Ω,Y)is a minimizer of(3.1).Then,for almost everywhere x0∈ Ω,we have the following holds:

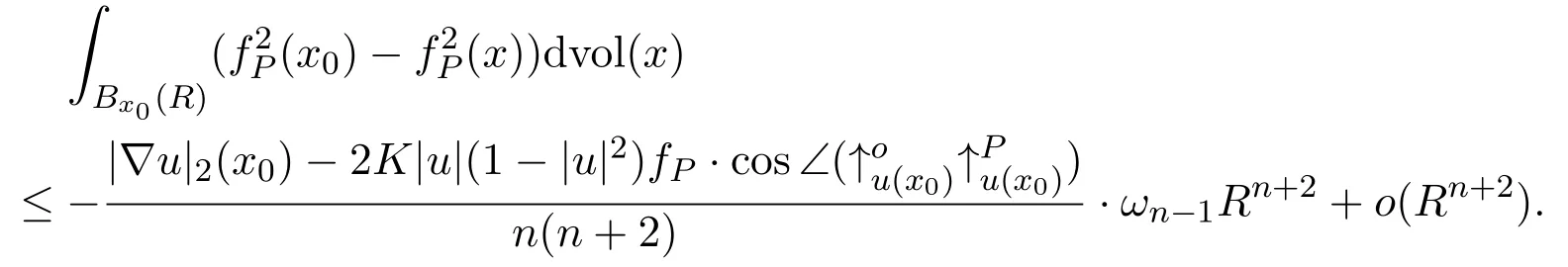
for every P∈Y,where fP(x)=dY(u(x),P).

ProofWe set a subset of Ω as

A:={x∈ Ω:xis smooth,Lipu(x)＜+∞,andxis a Lebesgue point of

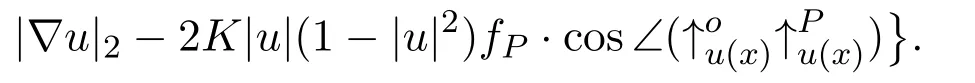
According to the above Corollary 4.1 and[31],we have vol(ΩA)=0.

Fix any pointx0∈A.For anyP∈Y,we consider the function on Ω

Then,from Lemma 3.2,we have

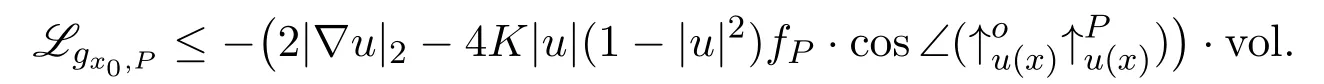
We denote

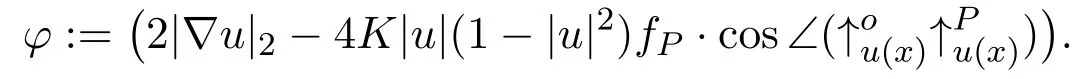
Sincex0is a Lebesgue point of the function-φ,by applying Proposition 2.4 to nonnegative function

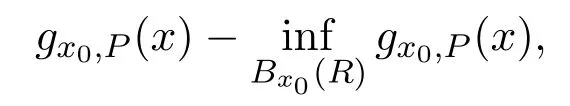
we can obtain

Denote

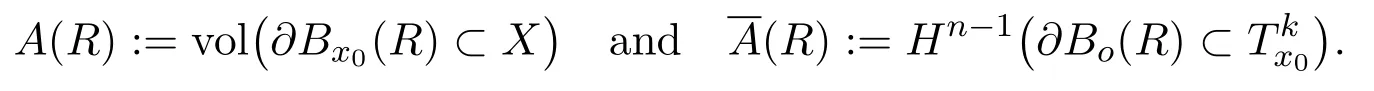
By applying co-area formula,integrating two sides of equation(4.23)on(0,R),we have

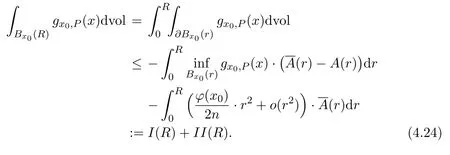
SinceXhas curvature ≥k,the Bishop-Gromov inequality states thatA(r)≤(r)for anyr ＞0.Hence we have

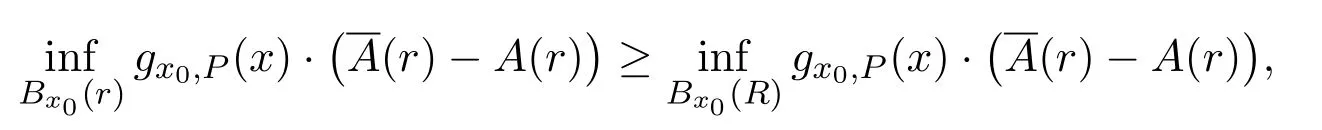
for any 0 ≤r≤R.So we obtain

By Lipu(x0)＜+∞and the triangle inequality,we have

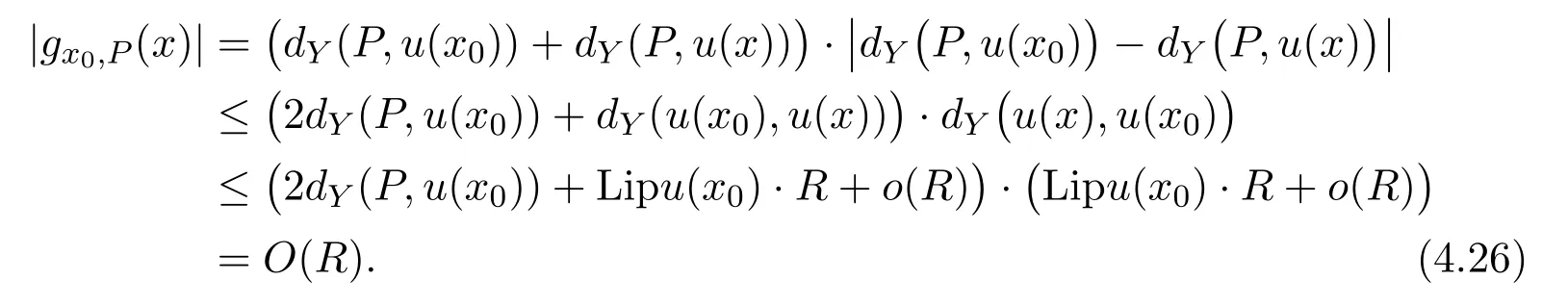
Sincex0ia a smooth point,from Lemma 2.1,we have

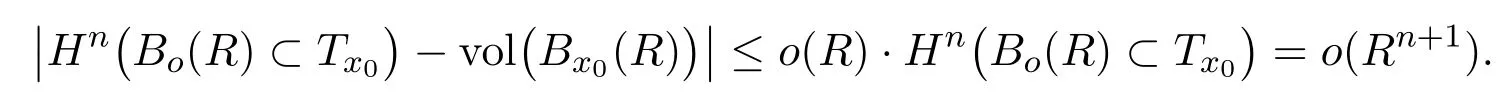
By using the fact thatx0is smooth again,and henceis isometric,we have

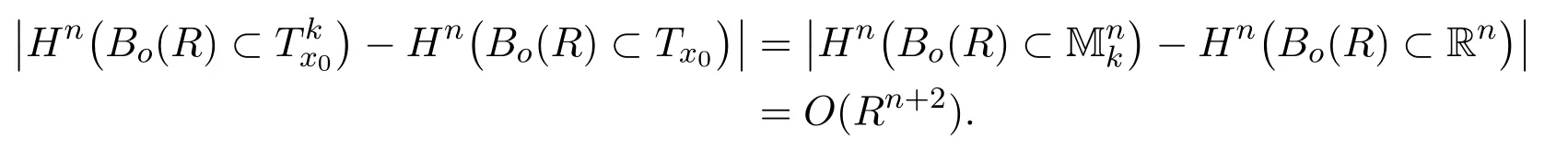
By substituting the above two estimates and(4.26)into(4.25),we can obtain

Now let us estimateII(R).Note thatx0is a smooth point.In particular,it is a regular point.Hence

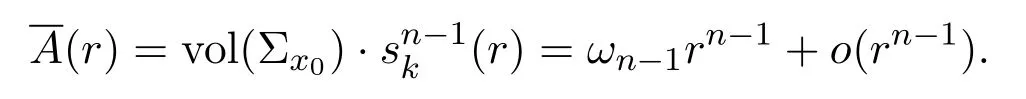
We have

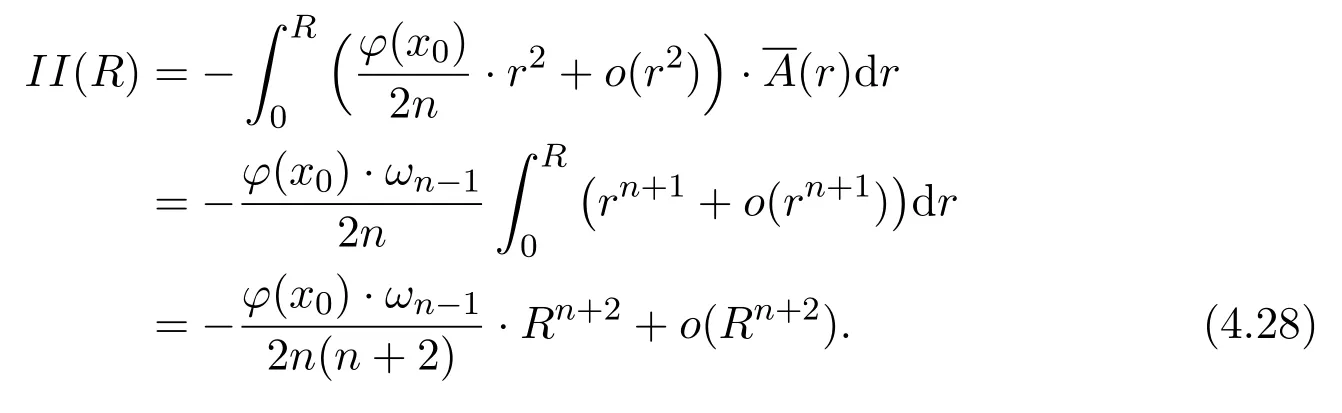
The combination of equations(4.24)and(4.27)-(4.28),we have

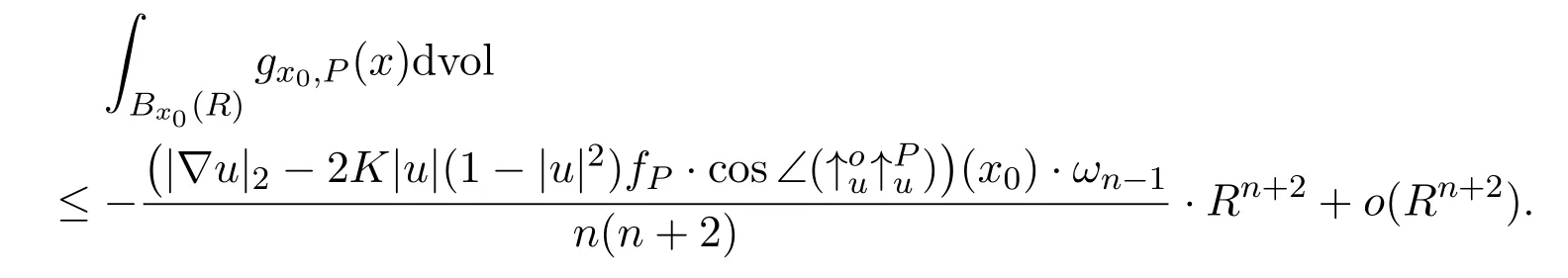
This is the desired estimate.Hence we complete the proof.

By using Lemma 4.3 and a similar argument in[40,Lemma 6.4],we can get the following mean value inequality.

Lemma 4.4Suppose that u∈W1,2(Ω,Y)is a continuous minimizer of(3.1).Given any z∈ Ωand P∈Y,we define a function wz,Pby

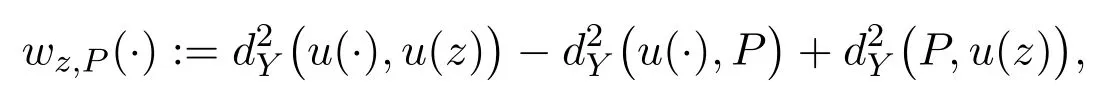
and fP(x)=dY(u(x),P).Given any sequence of positive numbers{ϵj}converging to0,there exists a sequence{εj}jconverging to0and a setNwithvol(N)=0such that the following property holds:Given any x0∈ ΩNand any P∈Y,the following mean value inequality

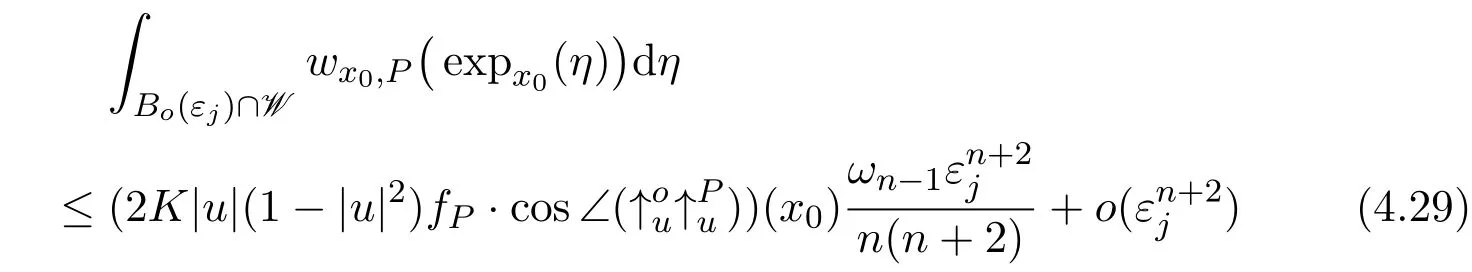
holds for any setW ⊂Wx0satisfyingProofFirstly,similarly to[40,(6.11)],we have,there exists a subsequence{εj}j⊂{ϵj}jand a set N with vol(N)=0 such that the following property holds:For anyx0∈ ΩN and anyP∈Y,we have

This comes from the combination of Lemma 2.6 withp=2,and Lemma 2.8 withR=εj.

Secondly,(4.29)follows from a similar argument of[40,(6.14)to(6.17)],by replacing[40,(6.16)]with the following inequality

We have completed the proof.

5 Lipschitz Continuity for the Minimizers

The Lipschitz regularity results,Theorem 1.2,will be proved in this section,by using a similar method in[40,section 6]. For the minimizer of the Ginzburg-Landau functional,we have to appropriately modify the construction of the auxiliary functions.

Let Ω be a bounded domain in ann-dimensional Alexandrov space(X,|·,·|)with curvature ≥kfor somek≤0.We continue to setY=C(Z)to be the Euclidean cone over a complete locally compact geodesic spaceZ,with curvature(Z)≤1.

Throughout this section,we always assume thatuis a minimizer of(3.1)with|u|≤1 on∂Ω. According to Lemma 3.1 and Theorem 4.1,we assume also that|u|≤1 on Ω and thatuis continuous.

5.1 A family of auxiliary functions with two parameters

Fix any domain Ω′⊂⊂ Ω. For anyt ＞0 and any 0 ≤λ≤1,we define the following auxiliary functionft(x,λ)on Ω′by:

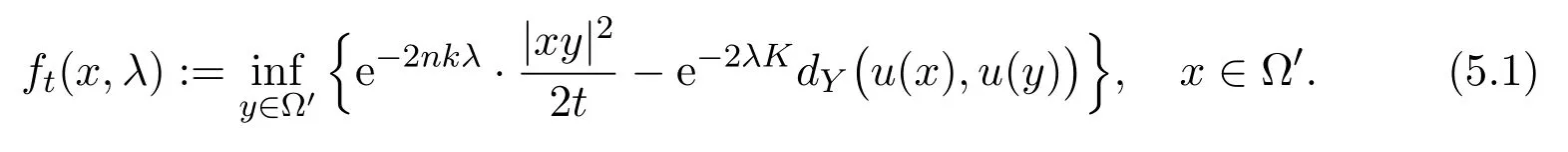
We denote bySt(x,λ)the set of all points satisfying(5.1),that is,

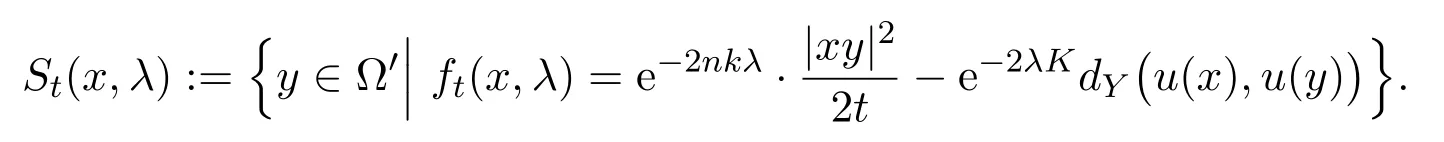
It is clear that

Given a functiong(x,λ)defined on Ω×R,we always denote byg(·,λ)the functionxg(x,λ)on Ω.The notationsg(x,·)andg(·,·)are analogous.

Similarly to[40,Lemma 6.1],we have the following lemma.

Lemma 5.1Fix any domainΩ′′⊂⊂ Ω′and denote by

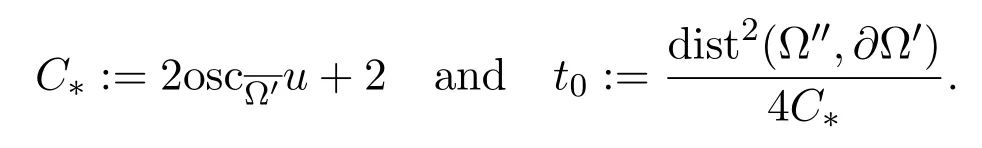
For each t∈(0,t0),we have:

(i)For each λ∈[0,1]and x∈ Ω′′,the set St(x,λ)̸=∅is closed,and

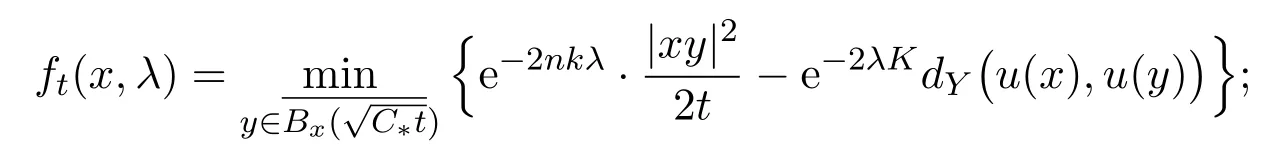
(ii)for each λ∈[0,1],the function ft(·,λ)is in C(Ω′′)∩W1,2(Ω′′),and

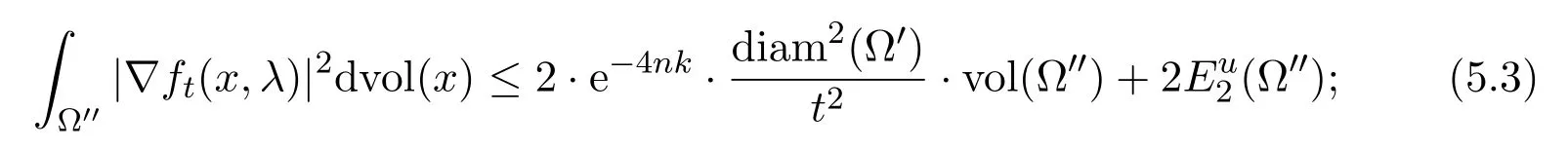
(iii)for each x∈ Ω′′,the function ft(x,·)is Lipschitz continuous on[0,1],and

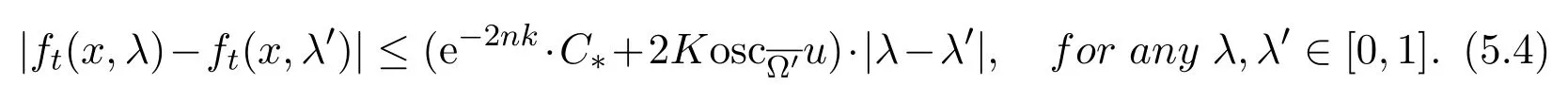
(iv)the function(x,λ)ft(x,λ)is inwithrespect to the product measure:=vol×L1,whereL1is the Lebesgue measure on[0,1].

Fix any domain Ω′′⊂⊂ Ω′and lett0be given in Lemma 5.1.For eacht∈(0,t0)and eachλ∈[0,1],the setSt(x,λ)is closed for allx∈ Ω′′,by Lemma 5.1(i).We define functionsLt,λ(x)andMt,λ(x)on Ω′′by

and

Similarly to[40,Lemma 6.2],we have the following lemma.

Lemma 5.2Fix any domainΩ′′⊂⊂ Ω′.For each t∈(0,t0),we have:

(i)The function(x,λ)Lt,λ(x)is lower semi-continuous inΩ′′×[0,1];

(ii)for each λ∈[0,1],

where the constant C∗is given in Lemma5.1.

(iii)the function(x,λ)Mt,λ(x)is lower semi-continuous inΩ′′×[0,1],and for each λ∈[0,1],we have

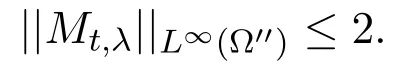
We now consider the estimate of∂ft/∂λ.

Lemma 5.3Fix any domainΩ′′⊂⊂ Ω′,for each t∈(0,t0),we have

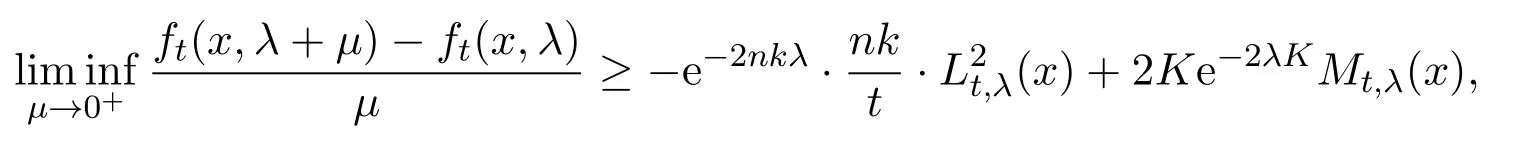
for any λ∈[0,1)and x∈ Ω′′.

Consequently,we have,for each x∈ Ω′′,by Lemma5.1(iii)

ProofLett∈(0,t0),λ∈[0,1)andx∈ Ω′′.For each 0＜ µ ＜1-λ,we take a pointyλ+µ∈St(x,λ+µ).By the definition offt(x,λ)andSt(x,λ),we have

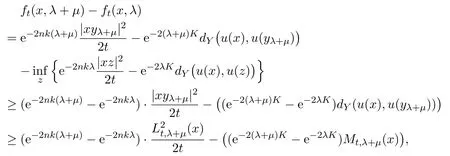
where we have usedk≤0.By the lower semi-continuity ofLt,λandMt,λ,we have

This proves the lemma.

An important trick in Alexandrov geometry is a method of perturbation,due to Petrunin[33].We summarize it in the following lemma.

Lemma 5.4(Petrunin's lemma of perturbation[33])Let U⊂X be a domain of M and u∈W1,2(U)∩C(U)satisfyLu≤λ·volon U for some constant λ∈R.Assume that A⊂U has full measure.Suppose that point x∗∈U is a minimal point of function u.

Then,for any δ ＞0,there exist a small domain Dδ⊂U and a δ-concave function fδdefined on Dδsuch that the function u+fδhas a minimal point xδin A∩Dδand|x∗xδ|＜ δ.

ProofFix anyδ ＞0.SinceMhas curvature ≥k,there exists a small positive numberδ1≪δso that the functionδ1|x∗·|2is(δ/2)-concave onU.Now the functionu+δ1|x∗·|2has a unique minimum point atx∗.

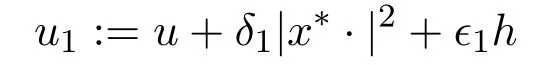
Let us take a ballB(x∗,r)so small that there exists a Perelman concave functionhdefined onB(x∗,r)(see Proposition 2.3).Take anϵ1＞0 suffice small so that the function has a minimum,sayx1,inB(x∗,r).According to[39,Lemma 4.15],we see that the pointx1is regular.By setting any positive numberϵ2,the functionu2:=u1+ϵ2|x1·|2has a unique atx1onThere exits a coordinate systemg=(g1,g2,···,gn)on a neighborhoodDaroundx1such thatgsatisfies the following:

(i)gis an almost isometry fromDtog(D)⊂Rn(see[4]);

(ii)all of the coordinate functionsgj,1 ≤j≤n,are concave([30]).

By using[39,Lemma 4.16],we conclude that,for arbitrarily smallϵ3＞0,there exists aV=(v1,v2···,vn)∈Rnwithϵ3＞vi≥0,1 ≤i≤n,such that

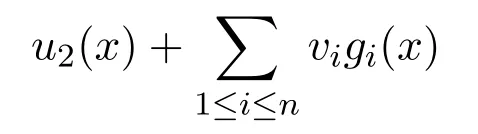
has a minimum point inA∩D.

Noting that the functionu+δ1|x∗·|2has a unique minimum point atx∗,the minimum point of

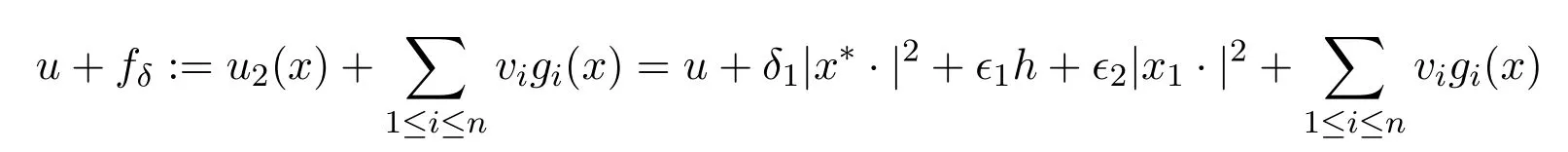
must converge tox∗asϵ1,ϵ2,ϵ3→0.Therefore,we can choose all ofϵ1,ϵ2andϵ3sufficiently small such that the minimum point ofu+fδis close tox∗.The proof is finished.

Remark 5.1In Lemma 5.4,ifU=U1×U2is a domain in a product Alexandrov spaceX1×X2and ifusatisfies≤λ·volX1×X2,then the functionfδin the assertion can be chosen to have the formf1(x1)+f2(x2),where L(2)is the Laplacian onU1×U2.

The following lemma is similar to[40,Lemma 6.7],which is the key to obtain a uniformly estimate forft(x,λ).For completeness,we give a detailed proof.

Lemma 5.5Given anyΩ′′⊂⊂ Ω′,there exists a constant t0＞0such that,for each t∈(0,t0)and each λ∈[0,1],the function xft(x,λ)is a super-solution of the Poisson equation

ProofAccording to Lemma 5.1,there exists a constantt0such that,for eacht∈(0,t0),we have̸=St(x,λ)⊂⊂ Ω′for any(x,λ)∈ Ω′′×[0,1].To prove the lemma,it suffices to prove the following claim.

ClaimFor each t∈(0,t0)and each λ∈[0,1],the function ft(·,λ)is a supersolution of the Poisson equation

for any θ ＞0.

We shall prove Claim by a contradiction argument.Suppose that Claim fails for somet∈(0,t0),λ∈[0,1]and someθ0＞0.According to Lemma 2.3,there exists a domainB⊂⊂ Ω′′such that the functionft(·,λ)-v(·)satisfies

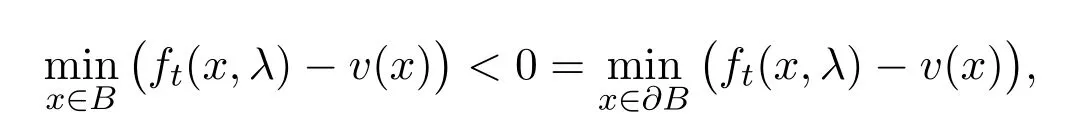
wherevis the(unique)solution of the Dirichlet problem

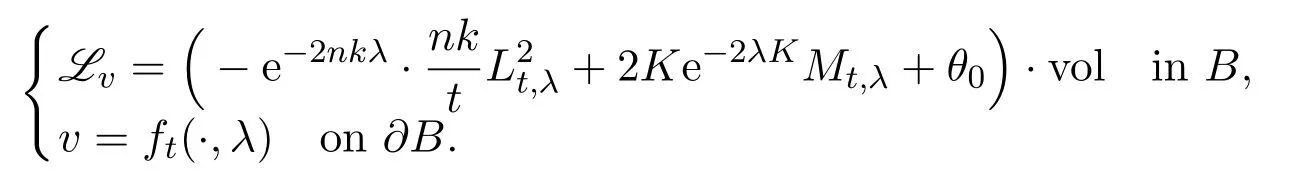
We say this case thatft(·,λ)-v(·)has astrict minimumin the interior ofB.

Let us define a functionH(x,y)onB× Ω′,by

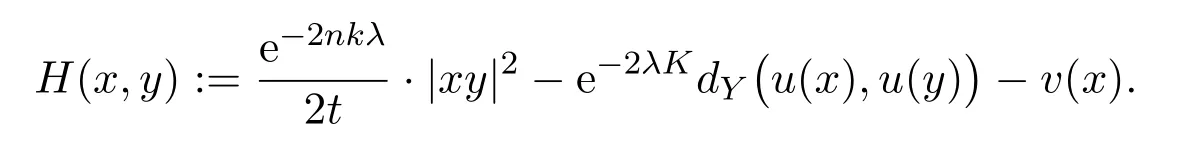
Moreover,we have

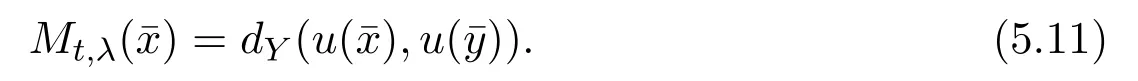
By the definition ofSt(,λ),we conclude thatH(x,y)has a minimum at(,).

Let A ⊂B×Ω′be the set of all points(xo,yo)∈B×Ω′satisfying the following properties:

1)xo̸=yo;

2)bothxoandyoare smooth;

3)geodesicxoyocan be extended beyondxoandyo;

4)pointxois a Lebesgue point ofMt,λ+θ0;

5)the mean value inequalities(4.29)hold,with some sequence{εj}jconverging to 0,for functionswxo,Pandwyo,Qfor anyP,Q∈Yand any corresponding sets satisfying(4.30).

According to Lemma 4.4 and noticing that the set of smooth points has full measure,it is clear that the set A has full measure onB× Ω′.

Take a subsequence of numbers{εj}j,denoted again{εj}j,such that the second variation of arc-length,Proposition 2.2,holds for an isometryT:Txo→Tyo.Put W:=Wxo∩T-1(Wyo),which satisfies(4.30).

Notice that the function|··|2is semi-concave onB×Ω′⊂X×X. From Proposition 4.1 and that

we get that

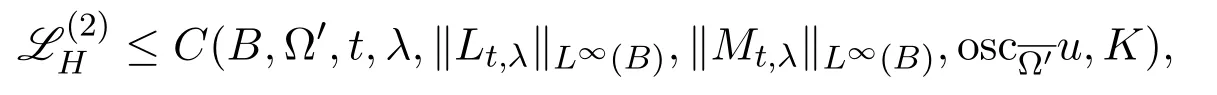
where L(2)is the Laplacian onB× Ω′.Now,by using Petrunin's perturbation,Lemma 5.4 and Remark 5.1,we conclude,for any fixedδ ＞0,that there existδconcave functionsγ1(x)andγ2(y)near¯xand¯y,respectively,such that the function

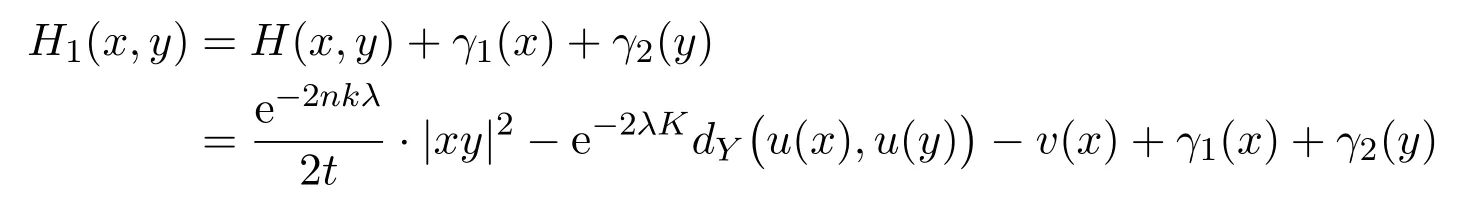
has a minimal point(xo,yo)∈A with

Let us consider the mean value

where

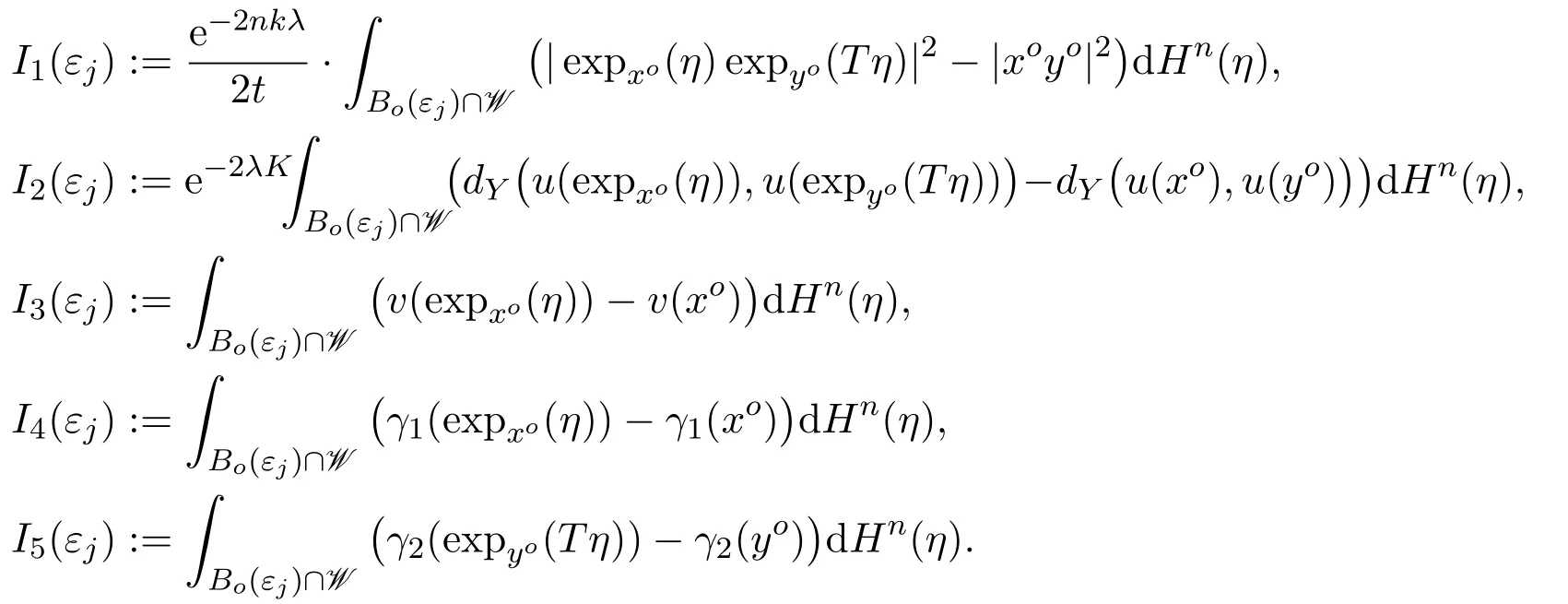
The minimal property of point(xo,yo)implies that

We need to estimateI1,I2,I3,I4andI5.

(i)The estimates of I1,I4andI5.

By using the second variation of arc-length Proposition 2.2,the estimate ofI1has been estimated in[40,(6.24)].That is,

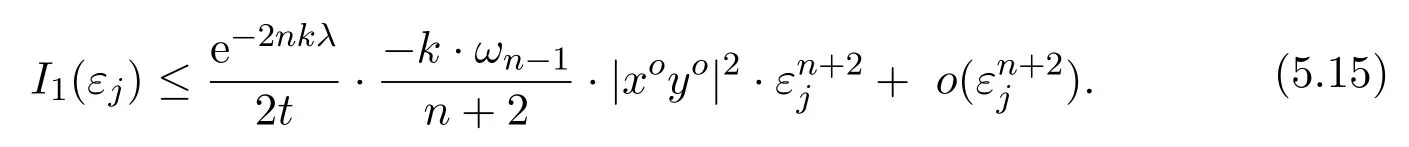
According to[40,Sublemma 6.8]and theδ-concavity ofγ1,γ2,we obtain

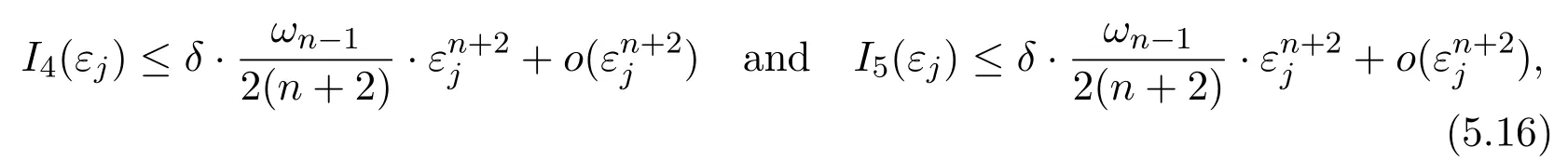
for anyj∈N.

(ii)The estimate of I2.

WhendY(u(xo,yo))̸=0,from the similar arguments as in[40,(6.27)to(6.28)],we obtain

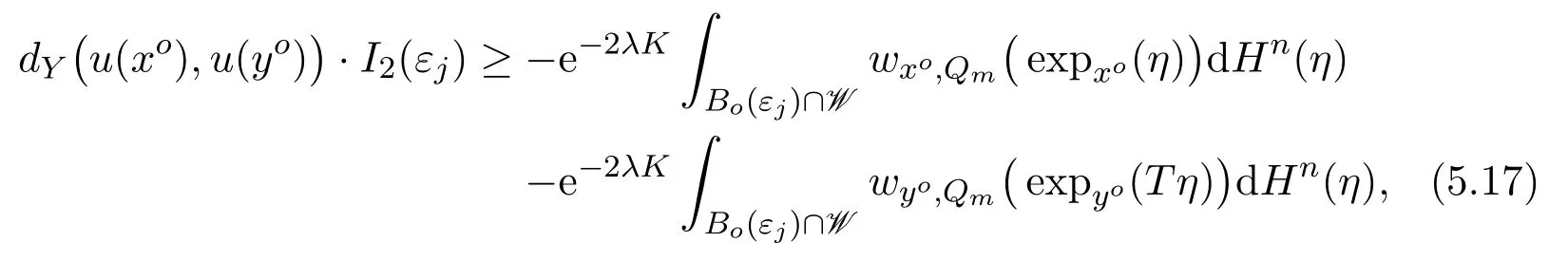
see Lemma 4.4 for the definitions of,Qmand,Qm.Thus,the combination of(5.17)and Lemma 4.4,we have

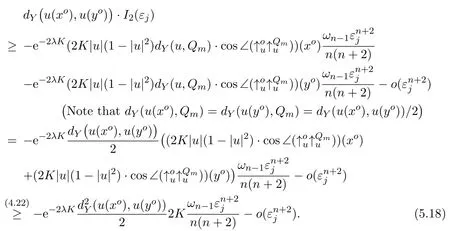
IfdY̸=0,then this inequality implies that

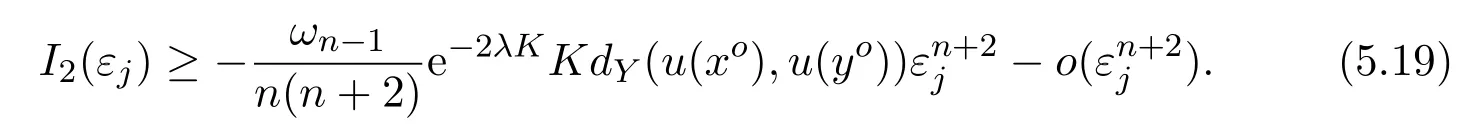
IfdY=0,then it is simply implied by the definition ofI2thatI2(εj)≥0 for allj∈N.Hence,the estimate(5.19)always holds.

(iii)The estimate of I3.

By setting the function

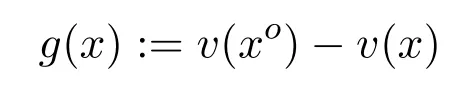
onB,we haveg(xo)=0 and

By using the same argument in[40,page 38]for estimatingI3there,and by replacing the functionin[40,page 38]bywe can obtain the estimate ofI3here

for anyj∈N.

Let us recall equation(5.13),(5.14)and combine all of estimates fromI1toI5.That is,equations(5.15),(5.19),(5.20),and(5.16).We can obtain

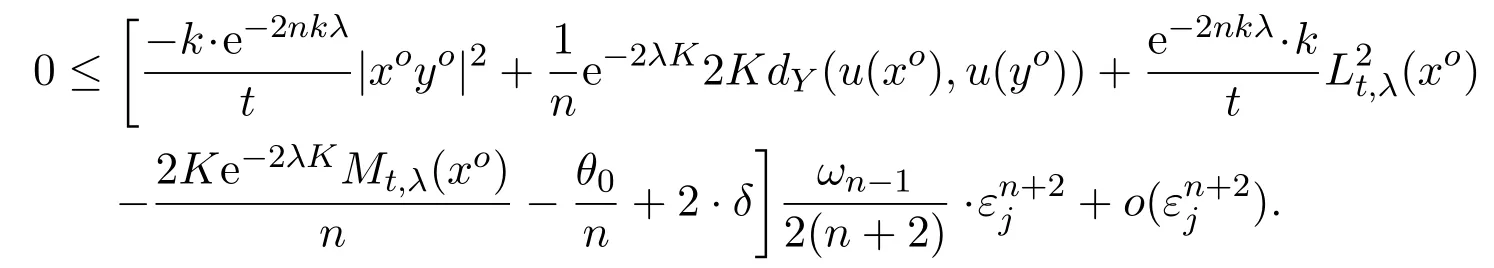
Thus,for any fixedδ ＞0,we have

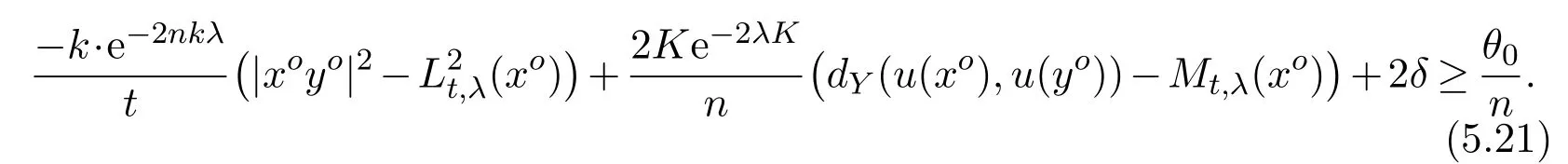
Notice that bothLt,λandMt,λare lower semi-continuous(see Lemma 5.2),and that(5.10)-(5.11)and(5.12),we know that the left hand side of(5.21)less thatκ(δ),for some functionκ(δ)with=0. Here we have used that-k≥0.Therefore,an contradiction arises when we chooseδto be sufficiently small in(5.12).This completes the proof of Claim,and hence that of the lemma.

In the following,similarly to[40,Proposition 6.13],by using Lemmas 2.5 and 5.5,we have that,the functionft(·,·)satisfies a parabolic differential inequality Lft(x,λ)≤∂ft/∂λ.Precisely:

Proposition 5.1Given anyΩ′′⊂⊂ Ω′,there exists a t∗＞0,such that,for each t∈(0,t∗),the function(x,λ)ft(x,λ)is a super-solution of

on the cylinderΩ′′×(0,1).

5.2 Lipschitz continuity for minimizers

In this subsection,we will prove our main result,Theorem 1.2.

Fix any domain Ω′⊂⊂ Ω,for anyt ＞0 and any 0 ≤λ≤1,the functionft(x,λ)is given in(5.1).We set

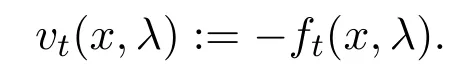
Then,by(5.2),we have

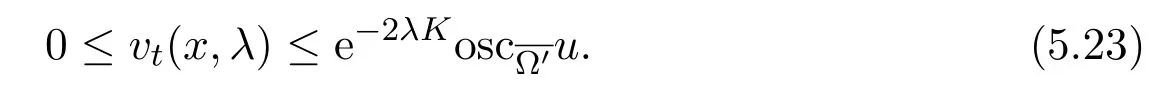
Along the same argument of[40,Lemma 6.15],by using(5.23),we have:

Lemma 5.6Let R≤1and ball Bq(2R)⊂⊂ Ω′. Suppose that t∗is given inProposition5.1forΩ′′=Bq(2R).For each t∈(0,t∗)and λ∈(0,1),we define the function x→|∇+vt(x,λ)|on Bq(2R)by

where a+=max{a,0}.Then,there exists a constant C1(n,k,R)such that,for any0＜s ＜1/4,

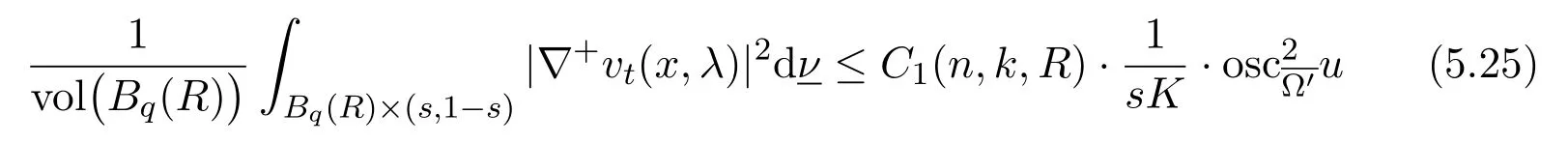
holds for all t∈(0,t∗).

Now we are in the position to prove Theorem 1.2.

Proof of Theorem 1.2Let us fix a ballBq(R)withBq(2R)⊂ Ω and denote byΩ′=Bq(R).Let¯t=minwheret∗is given in Proposition 5.1 for Ω′′=Bq(R/2).Denote by

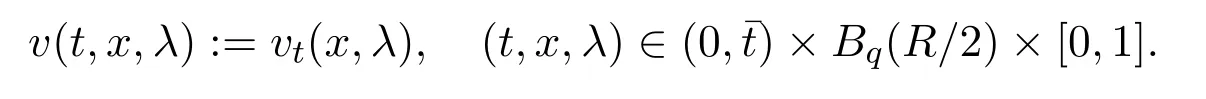
According to Proposition 5.1,for eacht∈(0,¯t),the functionv(t,·,·)is a sub-solution of the heat equation on the cylinderBq(R/2)×(0,1).

Next,similarly to[40,Sublemma 6.16],we want to estimate.

Sublemma 5.1For any t∈(0,)and any(x,λ)∈Bq(R/4)×(0,1),we have

ProofBy replacingf(x,y):=in the proof of[40,Sublemma 6.16],we can prove this sublemma.

Similarly to[40,Sublemma 6.17],we have:

Sublemma 5.2For0＜s ＜1/4.We define a functionHs(t)on(0,¯t)by

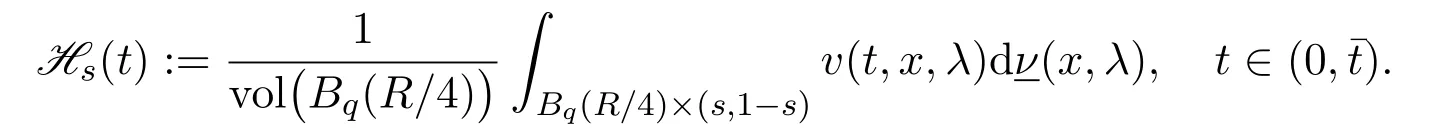
ThenHs(t)is locally Lipschitz in(0,).

Now let us continue to prove Theorem 1.2.

Fixed everyt ＞0,by Sublemmas 5.1 and 5.2,and the dominated convergence theorem,we have

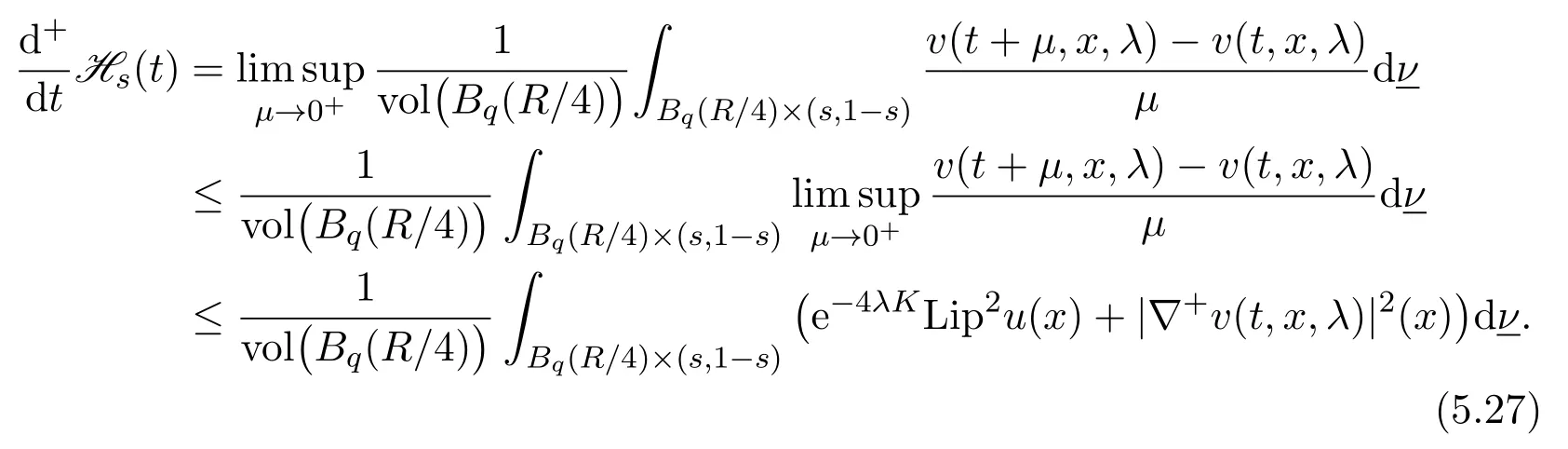
Use Corollary 4.1 to obtain

Here and in the rest of the proof,all of constantsC1,C2,···,depend only onn,kandR.Recall Lemma 5.6 that

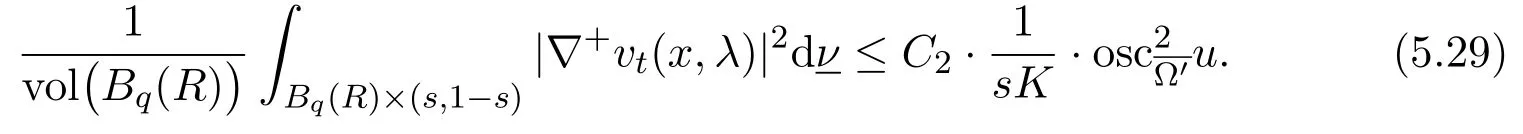
The combination of(5.27)-(5.29)implies that

where we have used the doubling property that vol.Denoting by

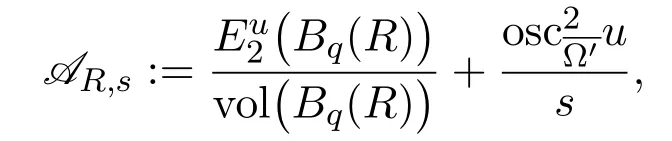
we have

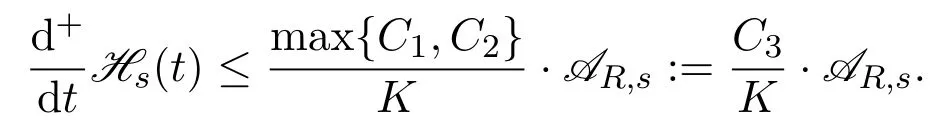
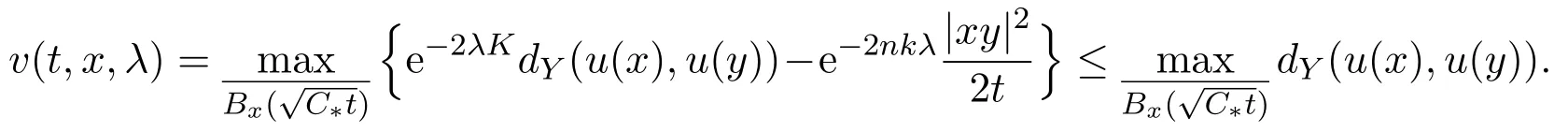
Note thatuis(Hlder)continuous,we deduce thatis bounded from(5.23),we can use dominated convergence theorem to conclude that=0.By combining this with Sublemma 5.2 and,we have

for anyt∈(0,).

Let us recall Proposition 5.1 that,for eacht∈(0,¯t),the functionv(t,·,·)and a nonnegative sub-solution of the heat equation on the cylinderBq(R/2)×(0,1),hence so is the functionBy using Lemma 2.4,we can obtain

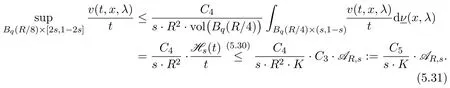
Recall thatK ＞2.We now chooses=1/(2K).Given anyx,y∈Bq(R/8),from the definition ofv(t,x,λ),we can apply(5.31)tov(t,x,1/K)and deduce

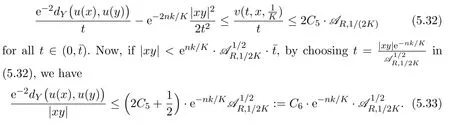
At last,letx,y∈Bq(R/16).If|xy|＜enk/K·then(5.33)holds.Ifwe can take some minimal geodesicγbetweenxandy.The triangle inequality implies thatγ⊂Bq(R/8).Choose pointsx1,x2,···,xN+1inγwithx1=x, xN+1=ysuch that|xixi+1|＜enk/K·for eachi=1,2,···,N.By the triangle inequality and(5.33),we have

This implies(5.33)still holds,that is,

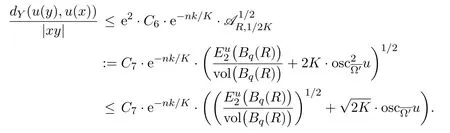
Therefore the proof of Theorem 1.2 is complete.

6 The Case where Y is A Space with 2-sided Curvature Bounds

Along the same method,we can give a Lipschitz regularity result when the target spaceYis a metric space with 2-sided curvature bounds. Recall the Ginzburg-Landau funtional(1.2),that is,

Here|u|o:=dY(u,o)for anyy∈Y.In this section,the pointo∈Yis arbitrarily fixed.We also write|·|instead of|·|ofor short.Precisely,we have the following theorem.

Theorem 6.1Let K ＞2.Let X be an n-dim Alexandrov space with curvature≥k and k≤0,Ω ⊂X be a bounded domain.Let Y be a complete locally compact geodesic space with l≤curvature(Y)≤0(in the sense of Alexandrov)and l ＜0.o∈Y is arbitrarily fixed.Then every minimizer u of(1.2)with|u|≤1on ∂Ωis locally Lipschitz continuous.Precisely,for any ball Bq(R)with Bq(2R)⊂ Ω,there exists a constant C(n,k,R),depending only on n,k and R,such that

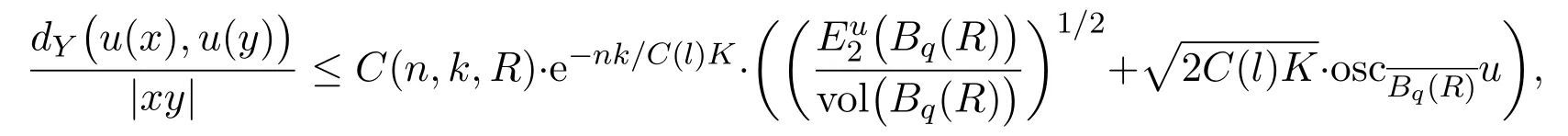
for all x,y∈Bq(R/16),where(Bq(R))is the energy of u on Bq(R)and

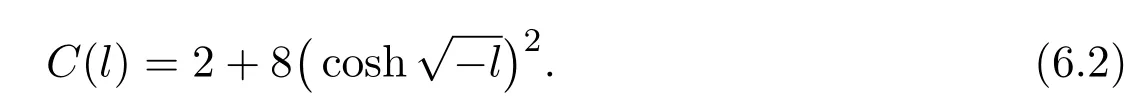
The proof of Theorem 6.1 is essentially the same as that of Theorem 1.2.We give some necessary details here.LetXbe ann-dim Alexandrov space with curvature≥kandk≤0,Ω ⊂Xbe a bounded domain.In this section,we set thatYis a complete locally compact geodesic space withl≤curvature(Y)≤0(in the sense of Alexandrov),andl ＜0.o∈Yis arbitrarily fixed.Suppose thatuis a minimizer of(6.1)with|u|≤1.

Similarly to Proposition 4.1,we have:

Proposition 6.1LetΩ,Y and u be as the above.Let f(x,y)=dY(u(x),u(y)).Then we have

in the sense of distribution onΩ × Ω,whereL(2)is the Laplacian onΩ × Ω,C(l)is defined in(6.2).

Sketch of ProofIn this case,we also have(4.20),wheregandhis defined by(4.18)and(4.19)respectively. We now estimateg+h. We denote bya=|u(x)|,b=|u(y)|,c=dY(u(x),u(y)),θ1=andRecall thatl≤curvature(Y)≤0. WhendY(u(x),u(y))̸=0,we haveand≤θ2≤,whereandare the corresponding comparison angles in the space form,andandare the corresponding comparison angles in the space formThus,whendY(u(x),u(y))̸=0,

By direct computation,we have

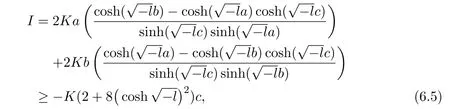
and

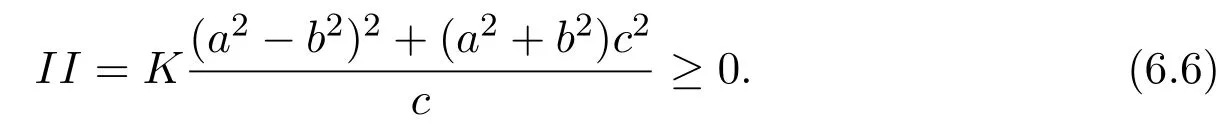
Thus,it follows from(6.4)-(6.6)that

that is,

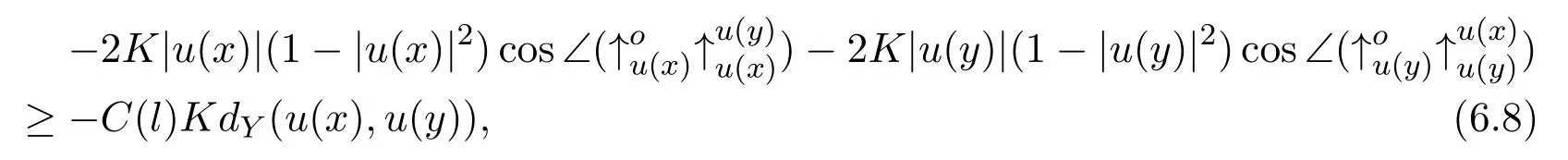
whendY(u(x),u(y))̸=0.It is easy to see that(6.7)also holds whendY(u(x),u(y))=0.Thus,Proposition 6.1 follows from(4.20)and(6.7).

Along the argument as in Corollary 4.1,we have:

Proposition 6.2LetΩ,Y and u be as the above.Then we have,for any ball Bq(R)⊂⊂Ω,there exists a constant C(n,k,R),depending only on n,k and R,such that

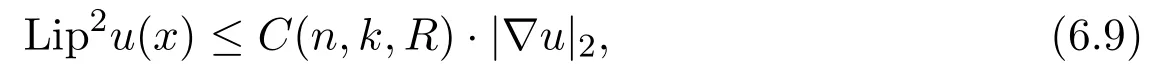
for almost everywhere x∈Bq(R/6).

We now give the outline of the proof of Theorem 6.1.

Sketch of the proof of Theorem 6.1

Step 1 Setting up the axillary functions.

Fix any domain Ω′⊂⊂ Ω.For anyt ＞0 and any 0 ≤λ≤1,define

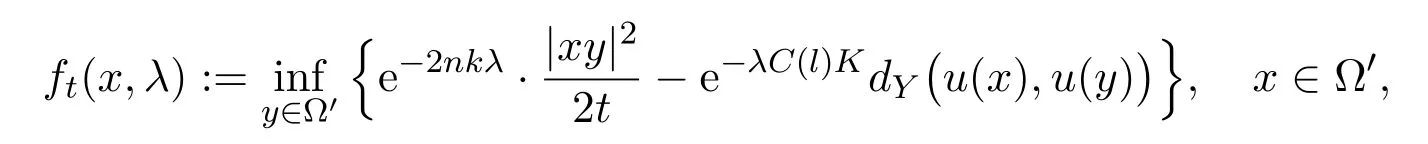
hereC(l)is given in(6.2).

Using the same arguments in the proof of Lemma 5.3,we get:

Lemma 6.1Fix any domainΩ′′⊂⊂ Ω′.For each t,we have

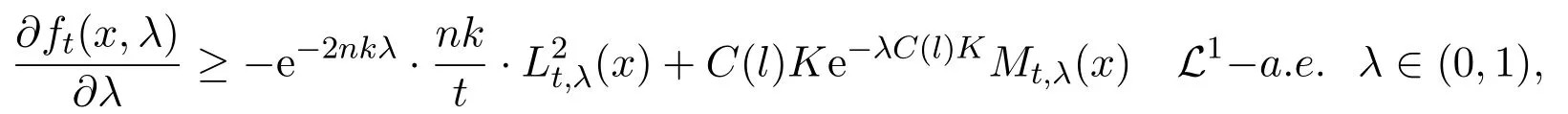
for each x∈ Ω′′.Where Lt,λ(x)is defined in(5.5),and Mt,λ(x)is defined in(5.6).

Step 2 Similarly to Lemma 5.5,we have:

Lemma 6.2Given anyΩ′′⊂⊂ Ω′,there exists a constant t0＞0such that,foreach t∈(0,t0)and each λ∈[0,1],the function xft(x,λ)is a super-solution ofthe Poisson equation

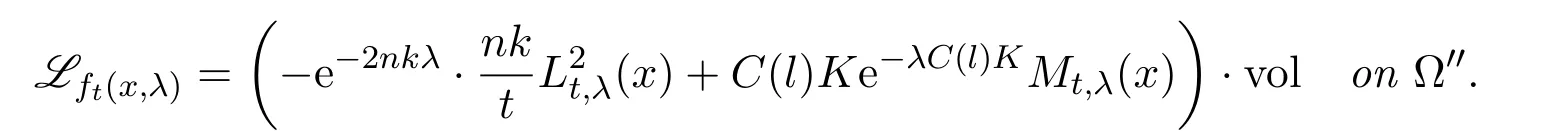
The proof of Lemma 6.2 is almost the same as that of Lemma 5.5,except for the estimate ofI2(5.18)is replaced by

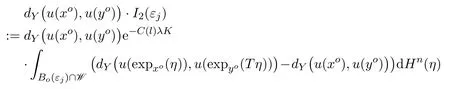
Step 3 Similarly to Proposition 5.1,by the combination of Lemmas 6.1 and 6.2,we have

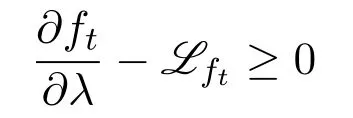
in the sense of Definition 2.4.Finally,applying same arguments as in Section 5.2,we conclude Theorem 6.1.