两个矩阵和Drazin逆新的推广式
2019-12-25杨晓英
杨晓英
(四川信息职业技术学院 基础教育部, 四川 广元 628017)
1 引言
设Cm×n表示m×n阶复矩阵的集合,A∈Cn×n, 若X∈Cn×n满足下列方程[1]:
Ak+1X=Ak,XAX=X,AX=XA, 则称X为A的Drazin逆, 记作X=AD。这里ind(A)=k, ind(A)表示A的指数,Aπ=I-AAD。矩阵的Drazin逆在奇异微分方程、迭代法、控制论中都有广泛的应用。近年来, 关于矩阵和的Drazin逆的表示,许多学者在不同条件下都做了很多讨论[1-11]。其中,文献[1]给出P2QP=0,P3Q=0,Q2=0和PQP2=0,QP3=0,Q2=0条件下体上两矩阵和的Drazin逆公式。在以上研究基础上,本文分别给出在P2QP+PQ2P=0,P2Q2+PQ3=0,P3Q=0,Q3P=0和Q3P+Q2P2=0,PQ2P+PQP2=0,PQ3=0,QP3=0条件下两矩阵和Drazin逆的表示。这推广了文献[1]中的一些结果。关于分块矩阵Drazin逆的表示一直是许多学者讨论的焦点,应用这些结论可以进一步讨论分块矩阵Drazin逆的表示。
下面给出几个重要的引理。
引理1[2]设A∈Cm×n,B∈Cn×m。则(AB)D=A((BA)D)2B。
引理2[3]设P,Q∈Cn×n, 如果PQ=0, 那么
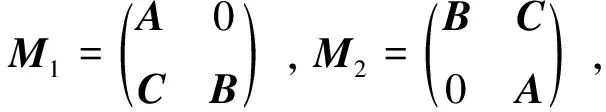
其中
2 主要结果
文献[1]给出在P2QP=0,P3Q=0,Q2=0和PQP2=0,QP3=0条件下两矩阵和Drazin逆的表示,本文我们应用以上引理分别给出在P2QP+PQ2P=0,P2Q2+PQ3=0,P3Q=0,Q3P=0和Q3P+Q2P2=0,PQ2P+PQP2=0,PQ3=0,QP3=0条件下两矩阵和Drazin逆的表示。这些条件比上面的条件更弱。
定理1设
若P2QP+PQ2P=0,P2Q2+PQ3=0,P3Q=0,Q3P=0。则
这里
J=(PD)2+PQX(PD)2+PQ(PQ)DX,
K=(Q2)D+QP(QP)DY+QPY(Q2)D,
其中,
ind(PQ)=s1, ind(P)=r1,ind(QP)=s2,ind(Q)=r2。
证明由引理1,可知
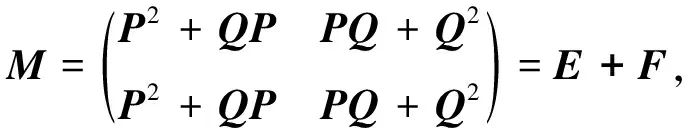
记
由P2QP+PQ2P=0,P2Q2+PQ3=0,得EF=0。
由条件P3Q=0,得E1E2=0, (E2)2=0。由引理2,通过计算得:
ED=E1D+E2(E1D)2。
又Q3P=0, 得F1F2=0, (F2)2=0。由引理2,得:
FD=F1D+F2(F1D)2。
再由引理3,得
其中
因此
进而
因此,结论显然成立。
定理2设
若Q3P+Q2P2=0,PQ2P+PQP2=0,PQ3=0,QP3=0, 则
这里
其中,H=(QD)2+(QD)2XPQ+X(PQ)DPQ,
L=(PD)2+Y(QP)DQP+(PD)2YQP,
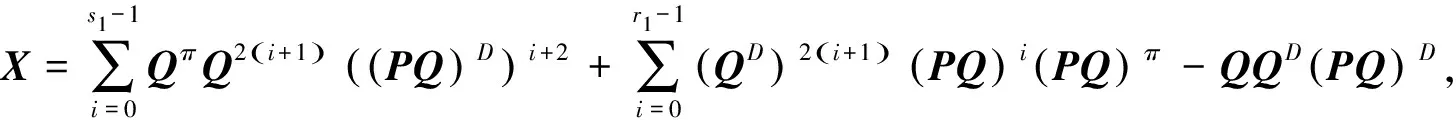
ind(Q)=s1, ind(PQ)=r1,ind(P)=s2,ind(QP)=r2。
证明由引理1,可知

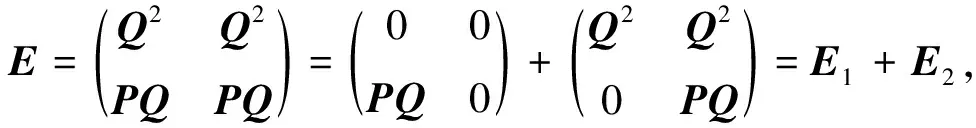
由Q3P+Q2P2=0,PQ2P+PQP2=0,得EF=0。
由条件PQ3=0,得E1E2=0, (E1)2=0。由引理2,得
ED=E2D+(E2D)2E1。
又QP3=0, 得F1F2=0, (F1)2=0。由引理2,得
FD=F2D+(F2D)2F1。
再由引理3,得
其中
因此
进而
这里,H=(QD)2+(QD)2XPQ+X(PQ)DPQ。L=(PD)2+Y(QP)DQP+(PD)2YQP。
因此,结论显然成立。
下面的推论是文献[1]中的重要结果。
推论1[1]设P,Q∈Cn×n,若P2QP=0,P3Q=0,Q2=0,则
其中ind(P2)=n1, ind(QP)=n2。
推论2[1]设P,Q∈Cn×n,若PQP2=0,QP3=0,Q2=0,则
其中ind(P2)=n1, ind(QP)=n2。
