压缩荷载作用下考虑T应力影响的裂纹扩展行为特性
2019-12-25李金凤何兆益李修磊
李金凤,何兆益,李修磊,杨 超
(1.重庆交通大学土木工程学院,重庆 400074; 2.重庆交通大学交通运输学院,重庆 400074;3.三峡大学三峡库区地质灾害教育部重点实验室,湖北 宜昌 443002)
在地质活动和人为工程扰动因素的作用下,岩石内部会产生大量节理、裂隙、微裂纹、空洞等缺陷,使得其力学性能趋于复杂化。这些缺陷在外部荷载的作用下逐渐扩展、贯通,最终导致地质或岩体工程灾害的发生。岩石的破坏实际是内部微缺陷的萌生、扩展、贯通和相互作用的过程。因此,针对岩石内部裂纹尖端的应力状态、起裂角度、扩展行为的研究具有重要的理论意义和工程价值。
传统线弹性断裂力学中裂纹的起裂、扩展属于裂纹尖端的局部效应,大多数国内外学者[1-2]基本上采用的是Williams[3]展开式中的r1/2奇异项(r为裂纹起裂的径向半径)来研究裂纹的起裂和扩展行为。然而,展开式中还存在非奇异项(即常数项)和高阶项O(r1/2)。对于高阶项O(r1/2),r趋近于0时可忽略,而非奇异项不受r的影响。一般情况下,将裂纹尖端的非奇异应力称为T应力[4]。忽略T应力会导致部分理论计算结果与试验结果存在明显偏差。例如,Ren等[5]采用有机玻璃材料制成半圆盘试件,通过三点竖向加载试验研究了复合裂纹断裂扩展行为;Williams等[6]采用中心含直裂纹的有机玻璃试件进行了三点弯拉试验;李部等[2]采用砂浆制成的类岩石试件进行了单轴压缩试验。然而,上述试验结果与Erdogan等[7]未引入T应力提出的最大周向应力(MTS)准则的计算结果相比差别较大。Tvergaard[8]采用修正的MTS准则,考虑平行于裂纹方向的T应力,研究了T应力对裂纹起裂和扩展行为的影响,证实在MTS准则中引入平行于裂纹的T应力能够有效提高理论值与试验结果的吻合程度。Andrews等[9]研究了双向拉伸荷载作用下裂纹的扩展特性。Ayatollahi等[10-11]采用有限元法并引入T应力,研究了Ⅰ型裂纹和Ⅰ-Ⅱ型复合裂纹尖端的应力分布,指出T应力会明显影响裂纹尖端最大周向应力,导致起裂角发生变化。刘梦和等[12-13]利用有限元分析探讨了空间复合型裂纹的应力强度因子与应变释放率的关系。何强等[14]基于岩石拉剪断裂试验,研究裂纹在载荷作用下起裂、扩展规律,探索断裂过程中裂纹的扩展行为。Tang等[15]通过引入平行于裂纹和垂直于裂纹的两个T应力分量,采用修正的MTS准则研究了拉-压组合荷载作用下T应力对裂纹起裂、扩展的影响。赵艳华等[16]考虑沿裂纹方向的T应力,发现T应力对Ⅰ-Ⅱ复合裂纹扩展的影响不可忽略,尤其是对纯Ⅱ型裂纹的影响尤为显著。
虽然已有大量关于T应力的研究,但主要集中于拉伸荷载作用对裂纹扩展的影响,拉伸荷载作用下裂纹处于张开状态,T应力仅包含与裂纹方向一致的非奇异应力项。然而,外部荷载作用下岩石往往处于挤压状态,此时微小裂纹大多为闭合形态,若裂纹表面存在滑移或滑移倾向时,裂纹表面必然存在摩擦作用,阻止裂纹面的相对滑移[17-18]。因此,裂纹的起裂和扩展与Ⅰ型张开裂纹的假设并不相符。针对压剪状态下闭合裂纹,Zhu等[19]和郑安兴等[1]分别采用边界配点法和伪力法综合考虑了裂纹表面的摩擦效应对裂纹尖端应力强度因子的影响,应用MTS准则分析了压剪状态下岩石的破坏特征。McClintock等[20]考虑裂纹表面的摩擦作用,修正了Griffth断裂破坏理论,但并没有考虑T应力的影响。Tang[21]通过分析压缩荷载下的应力状态,考虑了裂纹表面的摩擦作用,引入了平行于裂纹和垂直于裂纹的两个T应力分量(Tx和Ty),但忽略了切向分量Txy。赵彦琳等[22]虽然同时考虑了3个T应力分量的影响,但认为压缩荷载下只存在Ⅱ型裂纹而没有Ⅰ型裂纹,一定程度上会影响压缩荷载作用下计算结果的准确性。
本文结合Williams展开式中的奇异项和非奇异项,考虑裂纹表面的摩擦效应,同时引入3个T应力分量(Tx、Ty和Txy),推导裂纹起裂准则,分析T应力对裂纹尖端应力状态、最大周向应力、最大切向应力、裂纹起裂角和扩展行为的影响,并与已有试验结果进行比较分析,验证压缩状态下考虑T应力的合理性和有效性。
1 裂纹的应力强度因子计算
压缩荷载作用会引起岩石内部裂纹闭合,裂纹界面的摩擦约束作用会阻止裂纹的滑移扩展,从而影响裂纹尖端的应力强度因子。如图1所示,无限大板状岩石内部有一条长度为2a的裂纹,边缘均布双向轴压应力σ1和σ3,令σ1=σ和σ3=kσ1=kσ,其中k为侧压力系数,若k≥ 0则岩石处于压缩应力状态,若k<0则岩石处于拉-压组合应力状态。裂纹与主应力σ1方向的夹角为β(称为初始裂纹倾角)。由伪力法和叠加原理[20],可得到在t-n坐标系中,裂纹表面上的应力分量为
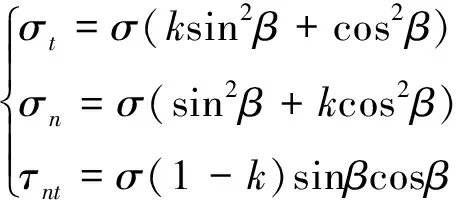
(1)
式中:σt、σn、τnt分别为t-n坐标系下沿t轴、n轴的法向应力和剪切应力。
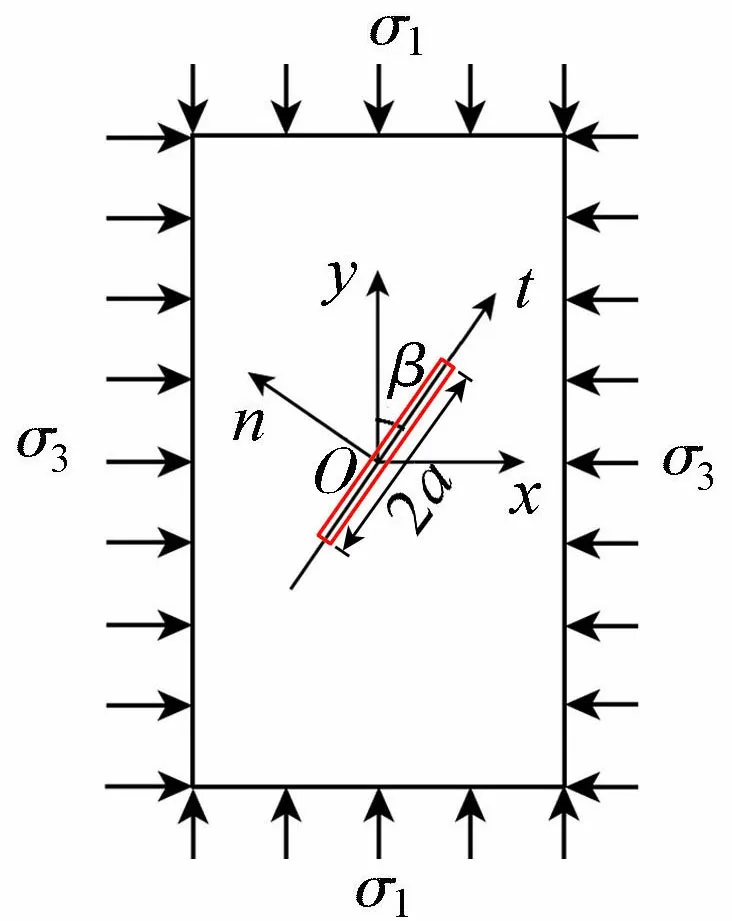
图1 双轴应力下的裂纹形态
考虑裂纹表面的摩擦作用,定义裂纹表面的摩擦系数为f,则由于裂纹上、下表面相对滑动或滑动趋势产生的摩擦力τ和有效剪应力τ′分别为
τ=fσn
(2)
τ′=τnt-fσn
(3)
利用Muskhelishvili复变函数理论和Riemanm-
Hilbert问题的理论解法,可得到裂纹表面应力的基本解[23]为

(4)
式中:Φ(z)为复变函数;z为自变量。裂纹尖端附近的应力强度因子K可由下式进行计算:
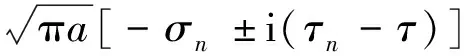
(5)
式中:KⅠ和KⅡ分别为Ⅰ型和Ⅱ型裂纹尖端的应力强度因子,由式(5)并联立式(1)~(3)可得KⅠ和KⅡ分别为

(6)

(7)
需要注意的是,虽然压剪应力状态下张拉型裂纹应力强度因子KⅠ没有意义,但会导致裂纹尖端应力场发生改变。由式(7)可知,随着摩擦系数的增大,裂纹尖端的应力强度因子KⅡ逐渐减小。
2 裂纹尖端的应力场
如图2所示,θ为岩板内部裂纹的起裂角,裂纹尖端的应力场可以表述为[3]
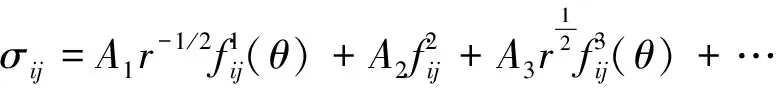
(8)
式中:右端第1项为奇异应力项,该项在裂纹尖端起主导作用,A1为应力强度因子KⅠ或KⅡ;第2项为非奇异项(即常数项),又称T应力,其大小与r无关,A2为非奇异应力,直接作用于裂纹表面[24];fij为与起裂角无关的无量纲项;第3项及后续项为r的高阶项,可以忽略。考虑T应力的裂纹尖端应力场的方程为

(9)
式中:σx、σy、τxy分别为x-y坐标系下裂纹尖端沿x轴、y轴和切向的应力。
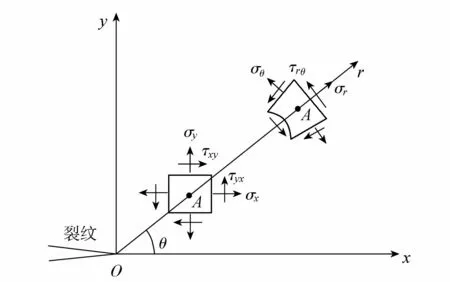
图2 裂纹尖端应力分布
极坐标系下,裂纹尖端应力场的方程式为
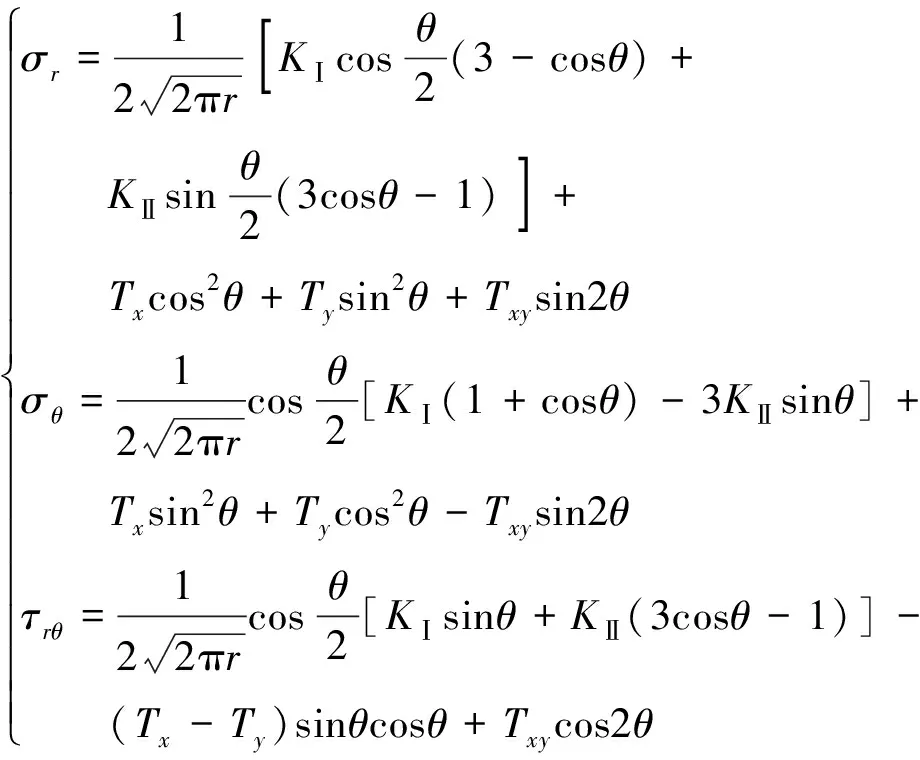
(10)
式中:σr、σθ、τrθ分别为极坐标系下的径向应力、周向应力和剪切应力。若σθ为正值,说明材料处于张拉应力状态;若为负值,说明材料处于挤压应力状态。
在式(1)中, 当σn>0时,裂纹处于张开状态,因而可以认为裂纹表面不存在摩擦作用,T应力(Tx、Ty、Txy)可定义为
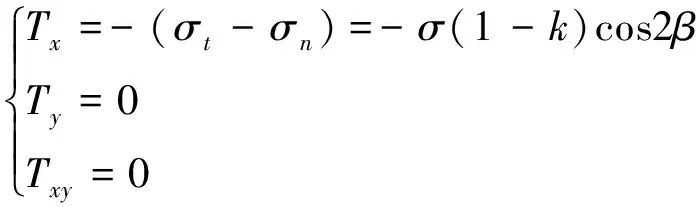
(11)
当σn≤0时,裂纹处于闭合状态,裂纹表面存在摩擦作用,因而T应力(Tx、Ty、Txy)可定义为
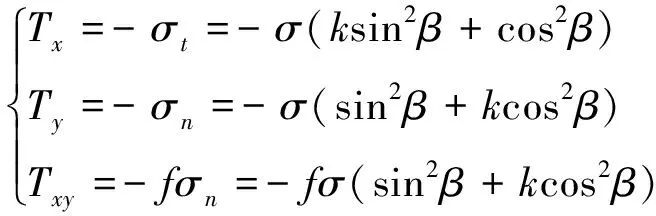
(12)
Li等[25]讨论了T应力分量Ty对裂纹扩展的影响,然而并没有研究初始裂纹倾角β与侧压力系数k对裂纹扩展的影响。Tang[21]考虑了Tx和Ty,忽略了Txy的作用,并没有得到闭合裂纹尖端完备应力场的理论解。式(11)(12)给出的T应力分量中考虑了β和k两个变量的作用。
3 考虑T应力的断裂准则
针对裂纹的起裂和扩展问题,一些学者提出了几种常用的断裂判据,主要包括MTS准则、最大能量释放率(MERR)准则、最小应变能密度(SED)准则、局部对称性(LS)准则、临界距离(CD)准则等[26]。其中,MTS判据应用最为广泛,该准则认为裂纹沿着最大周向应力σθmax方向起裂扩展,适用于抗拉强度明显小于抗剪强度和抗压强度的脆性材料(如岩石)。为此,本文将按照MTS准则,同时考虑T应力对裂纹的起裂、扩展行为的影响,裂纹起裂扩展应满足如下条件:

(13)
将式(10)代入式(13),可得起裂角需满足下列方程:
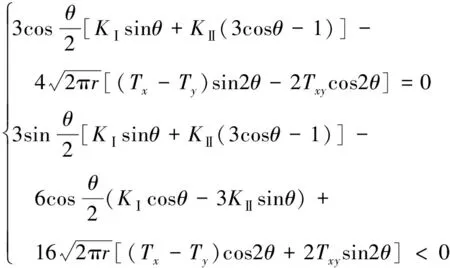
(14)
当裂纹起裂角θ确定后,通过考虑裂纹尖端临界半径rc的情况,由式(10)便可得到裂纹起裂时的临界周向应力σθc为
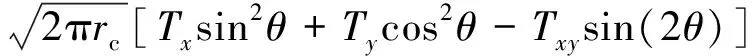
(15)
Bobet[27]使用最大剪应力准则(MSSC)对岩石内部裂纹的起裂角和应力进行了预测,发现该准则能够很好地描述试验过程中裂纹的扩展行为。该准则认为,当剪切应力绝对值|τrθ|达到临界剪切强度τc,即|τrθ|≥τc时,裂纹开始扩展。
根据上述的MSSC和MTS准则,裂纹尖端可能发生张拉型开裂、剪切型开裂或者是张拉-剪切复合型开裂,具体情况如下:①如果σθmax<σθc而且|τrθ|max<τc,裂纹尖端将不会出现开裂的迹象;②如果σθmax≥σθc而且|τrθ|max<τc,裂纹尖端将发生张拉型开裂;③如果σθmax<σθc而且|τrθ|max≥τc,裂纹尖端将发生剪切型开裂;④如果σθmax≥σθc而且|τrθ|max≥τc,裂纹尖端将发生张拉-剪切复合型开裂,其中|τrθ|max为剪切应力绝对值的最大值。
4 考虑T应力的裂纹起裂理论分析
由式(10)可知,裂纹尖端的应力分布依赖于KⅠ、KⅡ、Tx、Ty、Txy和r,其中KⅠ、KⅡ、Tx、Ty和Txy与给定的β、k和f有关,可利用式(6)(7)(12)计算得到。Schmidt[28]和Golos等[29]根据MTS准则提出裂纹尖端过渡区临界半径rc的计算公式如下:
(16)
式中:KⅠC为Ⅰ型裂纹的断裂韧度。当考虑T应力的影响时,按下式将裂纹尖端临界半径rc进行归一化处理:
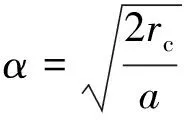
(17)
式中:α为归一化系数。根据Williams等[3,15,21,30]的试验结果和理论分析,计算过程中取α=0.1较为理想,即rc=0.005a。
4.1 T应力对周向应力和剪切应力的影响
k不同时T应力随β的变化如图3所示。由图3可以看出,Tx随着β的增大由k值逐渐增大到1.0,而Ty随着β的增大由1.0逐渐减小到k值;当β相同时,k越大对应的Tx和Ty越大;当β=45°时,Tx=Ty。由于Txy=fTy,可知当f为正值时,Txy与Ty有着相同的变化规律。
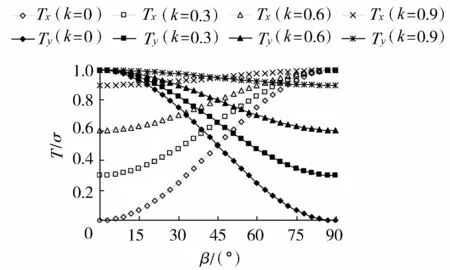
图3 k不同时T应力随β的变化
当β=30°,k=0.5,f=0.3时,T应力对裂纹尖端周向应力和剪切应力的影响如图4所示。由图4(a)可知,不考虑T应力时的周向应力均大于含T应力时的值,因而在压缩荷载作用下,忽略T应力的影响将使得裂纹尖端的周向应力增大,导致高估起裂荷载,所以T应力的存在起到阻止或延缓裂纹起裂和扩展的作用。分析T应力的影响时,若考虑Tx和Ty忽略Txy得到的最大周向应力偏小;若只考虑Tx得到的最大周向应力偏大。而本文同时考虑Tx、Ty和Txy的计算结果适中。
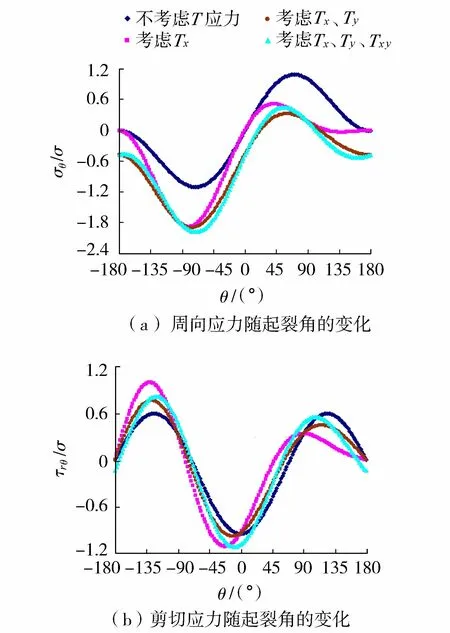
图4 T应力对周向应力和剪切应力的影响
由图4(b)可以看出,考虑T应力与否或只考虑部分T应力得到的剪切应力存在较大的差异,T应力对裂纹尖端应力状态的影响显著,因而在分析荷载作用下裂纹起裂和扩展的行为时需全面考虑T应力的影响,而不应忽略或只考虑部分T应力的影响。
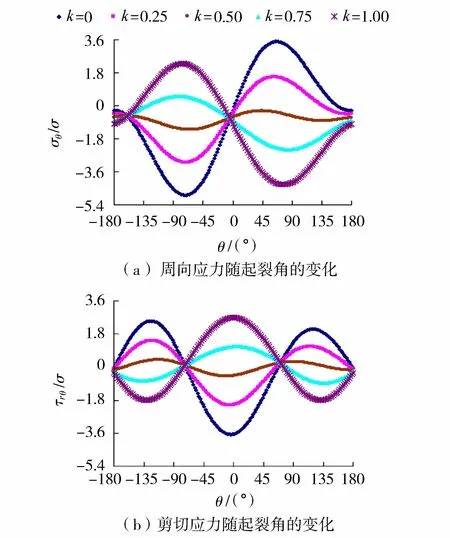
图5 侧向压力系数对裂纹尖端应力的影响
4.2 侧压力系数对周向应力和剪切应力的影响
图5给出根据式(10)计算得到的不同侧压力系数k值下归一化周向应力和剪切应力随起裂角θ的变化,其中,β=30°,α=0.1,f=0.3。由图5(a)可以看出,当θ介于0~180°时,裂纹尖端周向应力极值随着k值的增大由正值逐渐减小为负值,也就是说裂纹尖端由拉应力状态逐渐过渡到压应力状态;当θ介于-180°~0时,裂纹尖端周向应力极值随着k值的增大由负值逐渐增加到正值,说明裂纹尖端由压应力状态逐渐过渡到拉应力状态。以上表明,裂纹的起裂角随着k值的增加由正倾开裂逐渐向反倾开裂过渡(正倾是指θ与β的倾向一致;反倾是指θ与β的倾向相反)。
由图5(b)可以看出,裂纹尖端剪切应力τrθ随着θ的变化近似为“M”或“W”形状,且随着k值的增大逐渐由“M”形状变化到“W”形状;随着k值的增大,|τrθ|max呈现出先减小后增大的趋势。
4.3 初始裂纹倾角对周向应力和剪切应力的影响
图6给出了单轴压缩条件下(即k=0),初始裂纹倾角β对归一化周向应力和剪切应力随起裂角θ变化的影响,其中f=0.3。

图6 初始裂纹倾角对裂纹尖端应力的影响
由图6(a)可以看出,当θ介于0~180°之间时,β由5°增大到85°的过程中,周向应力的极值由正值逐渐增大到一定程度后再逐渐减小到负值;当θ介于-180°~ 0之间时,β由5°增大到85°过程中,周向应力的极值由负值逐渐减小到某一定值后再逐渐增大到正值。以上分析说明,随着β的增大,θ由正倾开裂逐渐向反倾开裂过渡。
由图6(b)可以看出,τrθ与θ之间的关系曲线表现为不规则的“M”或“W”形状,且随着β的增大由“M”形状逐渐过渡到“W”形状;|τrθ|max对应的θ分布在0°附近,随着β的增大,|τrθ|max呈现出先增大后减小再逐渐增大的趋势。
4.4 裂纹表面摩擦系数对周向应力和剪切应力的影响
图7给出了单轴压缩条件下不同裂纹表面摩擦系数f对应的归一化周向应力σθ/σ和剪切应力τrθ/σ随θ的变化,其中β=30°。由图7(a)可知,σθmax随着f的增加逐渐减小,对应的起裂角θ介于60°~68°,且θ随f值的增大呈缓慢减小的趋势。由图7(b)可知,|τrθ|max随着f值的增大逐渐减小,且对应的θ基本不受f值变化的影响。以上说明,相比k和β,f对裂纹尖端周围应力状态的影响要小得多。
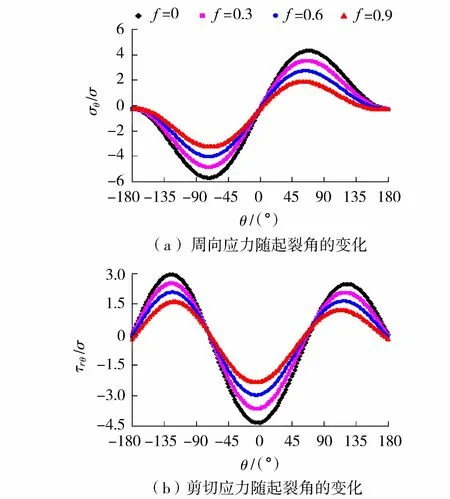
图7 裂纹表面摩擦系数对裂纹尖端应力的影响
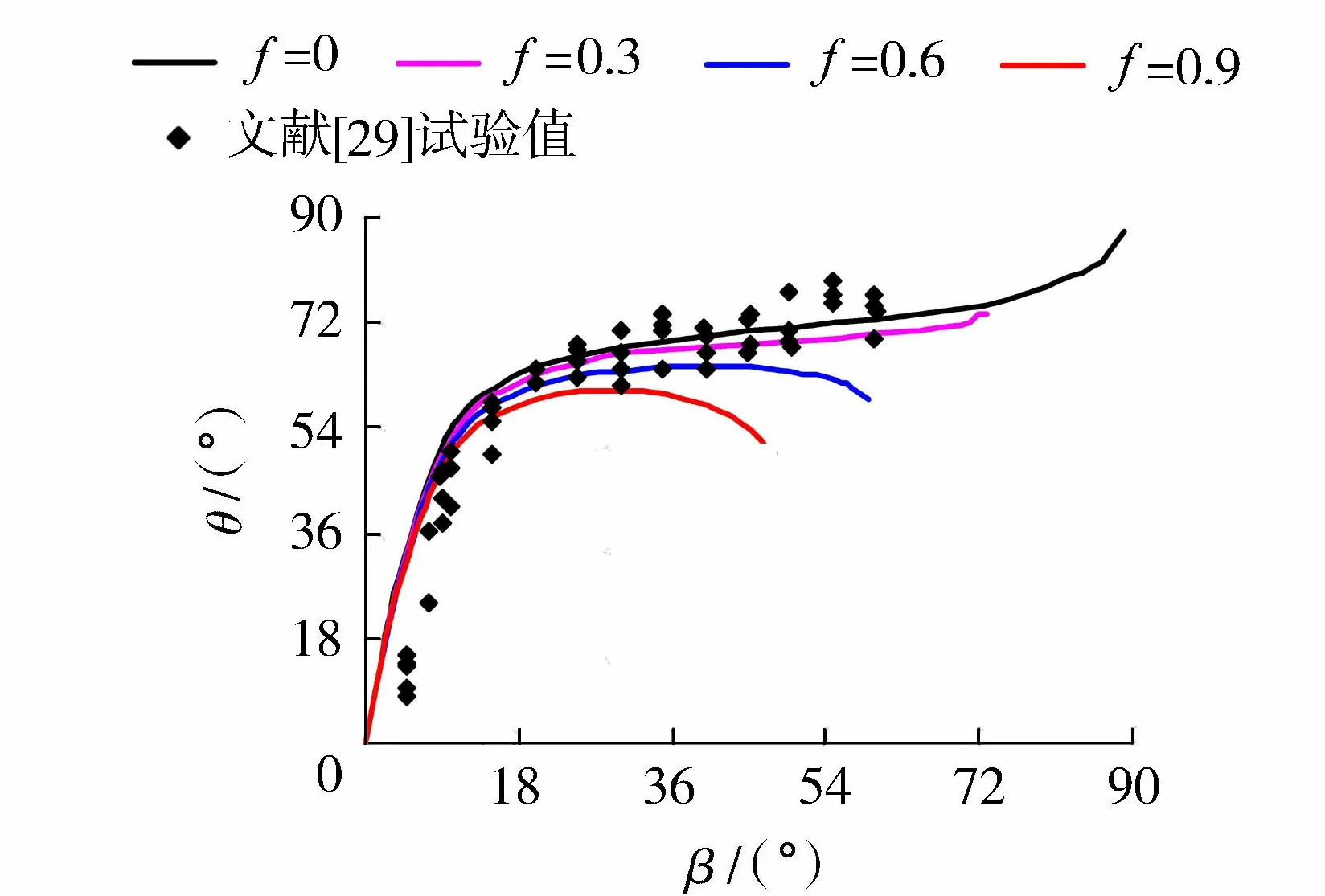
图8 起裂角理论值与试验结果的对比
5 计算值与试验结果对比分析
图8给出了单轴压缩条件下裂纹起裂角θ随初始裂纹倾角β的变化。由图8可以看出,理论值与文献[29]中的试验值有较高的吻合程度;不考虑裂纹表面摩擦作用时,张拉裂纹的起裂扩展总是先于剪切裂纹,但是随着f的增大,两种裂纹的优先发生严重依赖于材料内部的初始倾角。一般情况下,β越小越容易发生张拉开裂,β越大越容易发生剪切开裂。当f=0.3、0.6和0.9时,张拉型裂纹优先发生时对应的β范围分别为0~73.2°、0~59.1°和0~47.3°,其他角度范围均是剪切断裂优先发生。这里需要注意的是,随着f的增大,沿裂纹表面的摩擦作用更倾向于阻止裂纹的滑动开裂。因此,裂纹表面的摩擦作用能够抑制张拉裂纹的发生,却会增加剪切裂纹发生的概率。由图8还可以看出,β>15°时,θ对β值变化并不敏感;当β较小时,θ随β的增加而显著增大,而理论值相对试验值偏大,其主要原因在于试验所用试样尺寸有限,根据远场应力推求的裂纹尖端应力理论值与实际值存有一定差别。
5 结 论
a. 考虑T应力可有效减小裂纹尖端的周向应力,从而能够阻止或延缓裂纹的起裂和扩展,考虑非奇异项Tx、Ty和Txy所得到的σθmax和|τrθ|max介于只考虑Tx和考虑Tx和Ty所得到的值之间。
b. 裂纹表面的摩擦系数f越大,裂纹尖端的最大周向应力和剪切应力绝对值的最大值越小,考虑裂纹表面的摩擦效应一定程度上也能起到阻止或延缓裂纹起裂和扩展的作用。
c. 压缩荷载作用下,裂纹尖端的起裂角θ随着侧向压力系数k和初始裂纹倾角β的增大由正倾逐渐向反倾过渡;k和β越小,裂纹的起裂和扩展越容易发生张拉开裂;k和β越大,裂纹发生剪切开裂的概率越大。
