考虑融雪洪水跳跃变异的水库极限防洪风险复核
2019-12-25陈伏龙李绍飞何新林龙爱华
陈伏龙,李绍飞,冯 平,何新林,龙爱华,4
(1.石河子大学水利建筑工程学院,新疆 石河子 832000; 2.天津大学水利工程仿真与安全国家重点实验室,天津 300072; 3.天津农学院水利工程学院,天津 300384; 4.中国水利水电科学研究院流域水循环模拟与调控国家重点实验室,北京 100038)
近年来,随着人类活动对气候变化的不断影响,极端水文事件频频发生[1],多流域水文序列己经发生了明显的变化,使得洪水序列不再满足一致性假定[2]。利用传统水文频率分析已不能完全作为现如今水库极限防洪风险率的计算依据。因此,对水文非一致性序列的检验显得尤为重要。
水文序列变异的诊断问题是判断其是否为非一致性的首要条件。变异性检验的方法众多,不同方法得到的检验结果通常存在着差异,但总的来说,均是围绕着趋势性、跳跃性和周期性3个方面进行。2007年雷红富等[3]对趋势性和跳跃性成分检验方法的性能进行了比较研究;谢平等[4]在原先提出的综合诊断方法基础上发展了综合诊断系统。目前针对趋势和跳跃的诊断方法中,非参数法应用的较为成功,如Mann-Kendall[5-6]、Spearman[5,7]秩次相关检验法和贝叶斯方法[7]。为了保证水文序列频率分析的可靠性、代表性、一致性条件,研究工作者对水文非一致性分析做了大量的工作,既包括混合分布模型[7]、时变矩模型[8-9]、广义可加模型(GAMLSS)[10]等直接方法,也包括基于“分解-合成”理论的间接方法。Montanari等[11]明确指出了变化并不意味着非一致性,而一致性序列也不是一个一成不变的过程。因此,水文序列的非一致性并不能简单地根据统计检验结果得出,还需要一个明确的水文过程变化来进行验证。
在西北干旱山区融雪洪水是河川径流的主要来源,能很好地解决山区中下游绿洲生态系统的用水问题,但同时融雪洪水也同样存在安全风险。研究表明融雪洪水形成机理、发生发展过程与其他类型洪水相比,具有出现时间规律性强、洪峰宽广、量级相差大等特点,此研究结果为水库防洪渡汛提供了重要依据[12]。如果水文时间序列发生了变异,多数情况下水库对融雪洪水的汛期防洪调度也要进行调整,因此,对水库进行防洪极限风险复核分析就显得尤为重要。自20世纪50年代以来,我国对水库防洪调度的风险研究做了大量的工作。黄强等[13]采用定量分析方法中的马尔柯夫、概率统计、模糊数学风险分析方法对水库调度的风险问题进行了计算分析;熊明[14]根据风险计算的方法、原则及其适用性条件,利用随机模拟方法解决了人类活动影响下的概率分布问题;冯平等[15]采用模糊综合评价方法确定了合理的动态汛限水位,并提出了调整汛限水位的综合评价指标体系。在水库防洪调度的风险分析过程中,刁艳芳等[16]同时考虑了水文、水力、调度滞时和水位库容4种不确定性因素,基于拉丁超立方体抽样的蒙特卡罗模拟方法,建立了水库防洪调度风险分析模型,大大提高了风险分析模型的分析精度。在考虑气候因素及人类活动对径流过程影响的基础上,郭生练等[17]对新安江三水源产流模型及纳西地下线性水库汇流模型提出了新的洪水预报方案,从而显著地提高洪水预报精度;曹明亮[18]对SWAT模型进行了改进,提高了模型在变化环境下的准确性;黄凯等[19]采用水文变异诊断系统,对比分析了过去条件下、现在条件下的极限防洪风险率,从而进一步提高了环境影响下的预报精度。尽管水利研究工作者从不同的视角分析探讨了水库防洪调度的风险问题,同时取得了相对丰富的研究成果。但是对于变化条件下融雪洪水跳跃变异的水库极限防洪风险问题还有待解决。本文以玛纳斯河肯斯瓦特水库控制流域为研究对象,对此问题进行分析阐述,可为已建水库工程的防洪复核和未建水库工程的防洪规划提供科学指导依据。
1 研究区概况
玛纳斯河发源于天山北坡的依连哈比尔尕山,流域内地势由东南向西北倾斜,最高海拔5 442.5 m,最低海拔256 m,流向由南向北,是准噶尔盆地南缘最大的一条融雪型山溪河流,干流全长324 km(河源至小拐),河流从源头到出山口一带的长度为160 km。海拔3 600 m以上为终年积雪覆盖,有现代冰川分布,冰川面积608.25 km2,是各条河流的主要补给源。玛纳斯河在中山和前山区汇合了众多支流,流向东北,沿程有花牛沟、韭菜萨依、吉兰德、回回沟、希喀特萨依、哈熊沟、芦草沟、大(小)白杨沟、清水河等支流,均在肯斯瓦特水文站以上汇入干流。肯斯瓦特水文站是玛纳斯河干、支流汇合后的出山口控制站,海拔约910 m,控制流域面积为4 637 km2,多年平均径流量12.21亿m3。径流补给具有显著的垂直地带性,冰雪融水对河流的补给可以占到径流量的35.3%。肯斯瓦特水库具有防洪、灌溉、发电等综合利用功能。水库正常蓄水位990 m,最大坝高129.4 m,总库容1.88亿m3,控制灌溉面积21.09万hm2,属于大(2)型工程。水库设计洪水标准为500年一遇,相应的洪峰流量为2 382 m3/s;校核洪水标准为5 000年一遇,相应的洪峰流量为3 601 m3/s;下游防洪保护标准为50年一遇,相应的洪峰流量为1 249 m3/s。
2 融雪洪水特征序列非一致性检验
2.1 序列变异点检验
Pettitt非参数检验法最早由Pettitt[20]提出,并将其应用到变异点的检验。该方法对异常值不敏感,可以通过近似极限分布来计算检验统计P值[21]。通常将所研究的水文时间序列存在趋势性变化作为假设前提,并通过检验水文x时间序列要素均值变化的时间,来确定水文时间序列的变异时间。此方法采用Mann-Whitney统计量Ut,n来检验同一个总体x(t)的2个样本,其统计量Ut,n公式为
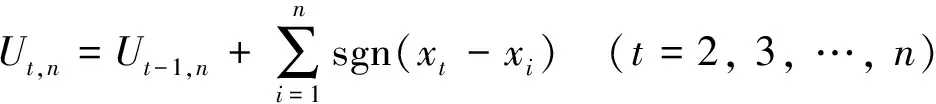
(1)
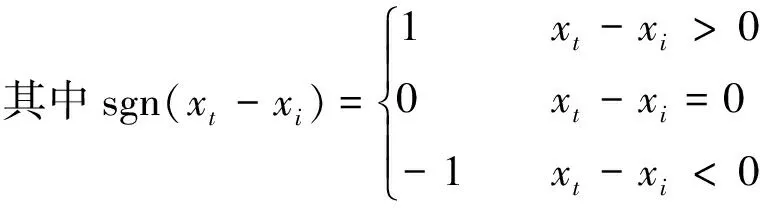
式中:n为样本长度。
Pettitt非参数检验的零假设表示水文时间序列无变异点,满足同一分布;非零假设表示水文时间序列存在变异点t,t前后两个子序列服从不同的分布规律。一般通过统计量Kn及相关概率P来判断水文时间序列是否变异,并确定其变异点的位置,其公式为
(2)
若P>0.95,则点t为显著性变异点,以此可检验出水文时间序列的一级变点,并结合物理成因分析便可判定水文时间序列x(t)的变异点。
对玛纳斯河肯斯瓦特水库控制流域融雪洪水特征序列进行变异点检验,结果如图1所示。年最大洪峰流量序列可能发生变异的年份为1992年、1993年和1994年;在有多个概率P值均大于0.95和变异点取值间距过小的情况下,取概率P值最大的变异点作为最可能发生的变异点。因此,年最大洪峰流量序列的变异点发生在1993年。
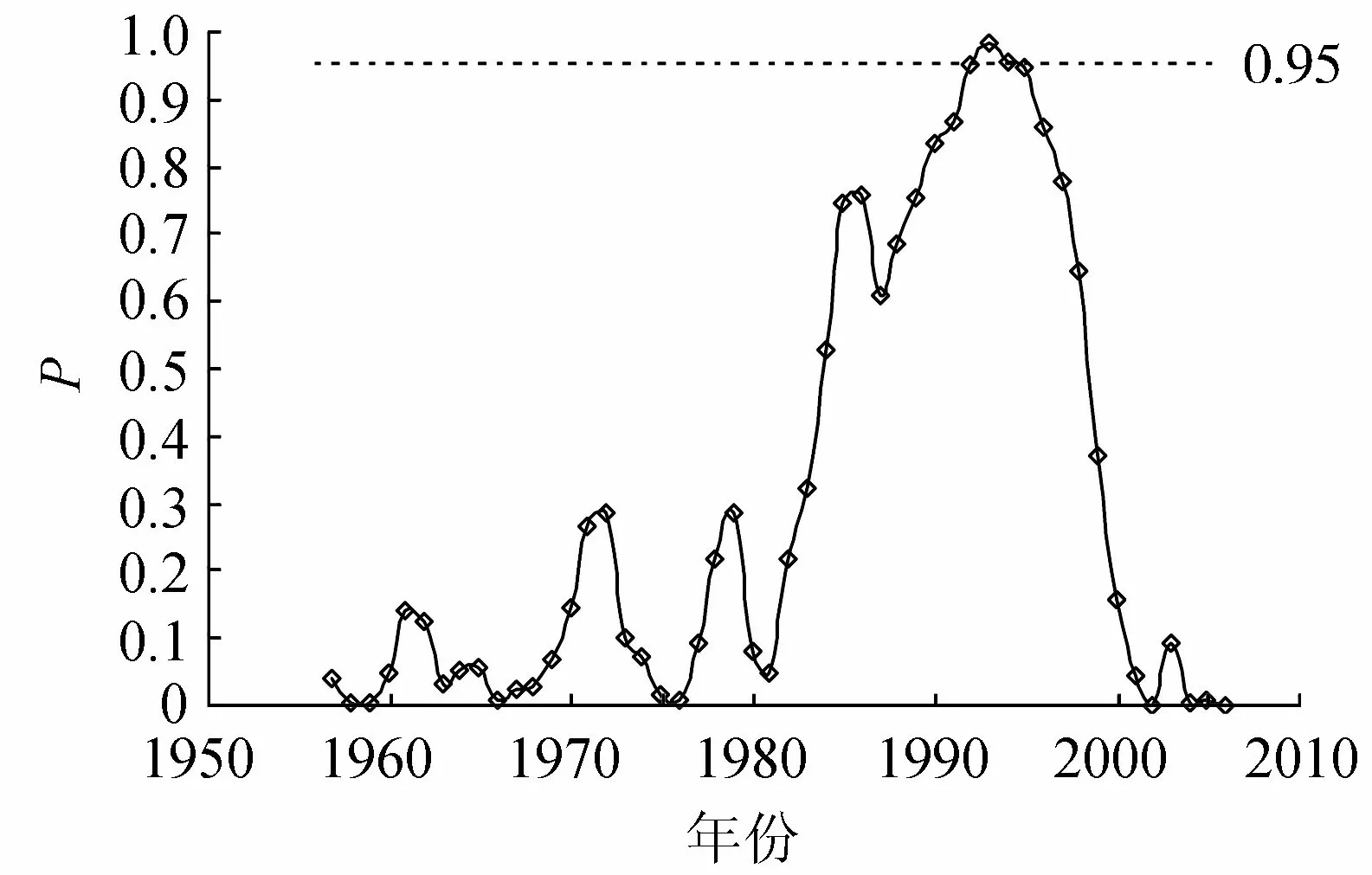
图1 年最大洪峰流量序列变异点分析
2.2 序列趋势检验
Mann-Kendall[22-23]非参数秩次统计检验方法在趋势检验中经常会受到水文时间序列自相关性的影响,在应用此方法前,先判断水文时间序列自相关性是否显著。对于水文时间序列(x1,x2,…,xn),首先对水文时间序列之后k阶的自相关性进行计算,若滞后一阶自相关系数在临界值范围之内,则其自相关性不显著,可直接对水文时间序列趋势性进行检验;否则,应先剔除水文时间序列的自相关性,再对新水文时间序列进行趋势性检验[24]。本文采用预置白Mann-Kendall检验[24](pre-whitening Mann-Kendall,PW-MK)来剔除其自相关性的影响。计算原水文时间序列Xn的一阶自相关系数r1,在δ的显著性水平下,采用双侧检验进行r1的显著性检验:
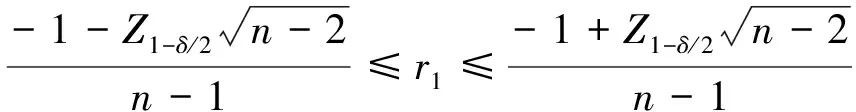
(3)
假设原水文时间序列为一阶自相关过程AR(1),采取预置白方法剔除原水文时间序列的自相关性,即
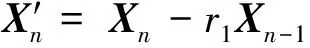
(4)

(5)
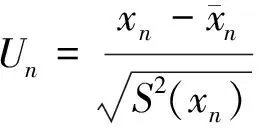
(6)
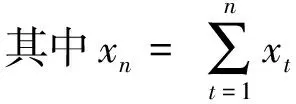
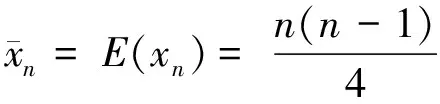
若Un>0,则水文时间序列(x1,x2, …,xn)呈上升趋势;反之,则呈下降趋势。若|Un|>Uα/2(|Uα/2|=1.96),则水文时间序列趋势性显著;反之,趋势性不显著。
对融雪洪水特征序列进行自相关性分析,结果如图2所示,年最大洪峰流量序列的一阶自相关系数均在临界值范围之内,自相关性不显著,可直接用原序列进行Mann-Kendall非参数趋势检验,结果见表1。年最大洪峰流量序列统计值小于1.96,表明未通过显著性趋势检验,变化趋势不显著。而在1957—1993年统计值小于-1.96,说明子序列通过了显著性趋势检验,并呈显著下降趋势;1994—2006年子序列未通过显著性趋势检验,变化趋势不显著。
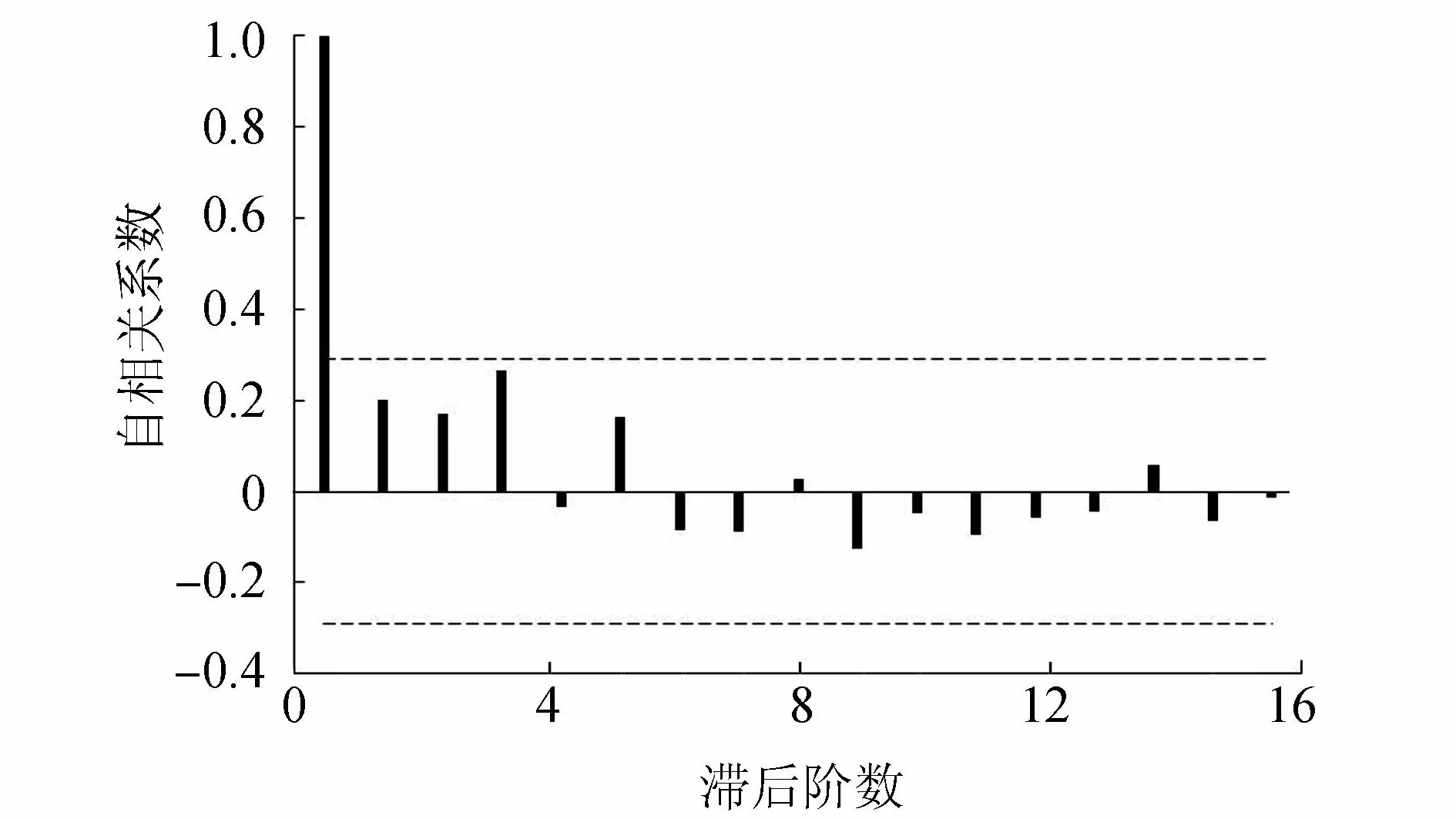
图2 年最大洪峰流量序列自相关关系
2.3 序列变异形式
基于肯斯瓦特水库控制流域年最大洪峰流量序列非一致性检验结果,序列局部趋势和跳跃均呈显著变化,采用效率系数R2[4]来评价年最大洪峰流量实测序列与趋势成分和跳跃成分的拟合程度。将趋势和跳跃两者效率系数较大的作为该时间序列的变异形式,其公式为
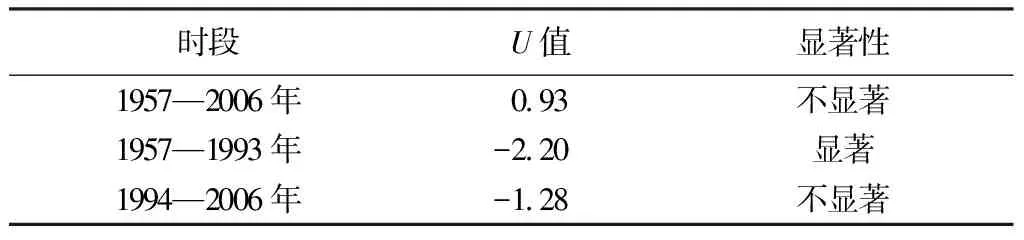
表1 年最大洪峰流量序列及子序列趋势分析
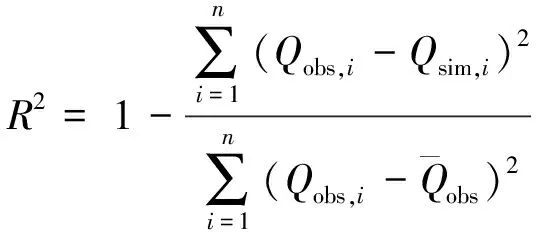
(7)
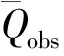
对肯斯瓦特控制流域年最大洪峰流量序列趋势和变异点的效率系数进行计算,其中趋势成分R2=6.38%,跳跃成分1993年R2=23.09%。由此可知,跳跃成分效率系数较大。从物理成因上分析,20世纪80—90年代流域上游流域人类活动干预较少,流域下垫面未发生剧烈变化,但是气候因素变化显著,综合作用下使得流域年最大洪峰流量序列呈上升趋势。因此,选择跳跃变异为年最大洪峰流量序列的变异形式。
3 融雪洪水特征序列一致性修正
3.1 序列分解计算
根据谢平等[25]提出的非一致性水文序列频率计算原理及方法,水文序列Xt由两种或两种以上成分组成,假设序列各组成成分满足线性叠加特征[26],水文序列Xt可表示为
Xt=Yt+Pt+St
(8)
式中:Yt为非周期成分;Pt为周期成分;St为随机性成分。本文只考虑非周期成分Yt(趋势或跳跃成分),以及St中的纯随机成分。
假设非一致性水文时间序列Xt的变异点为t0,t0前后的子序列物理成因均不相同,且t0之前的子序列反映环境变化情况不太显著的随机性成分,Xt可表示为
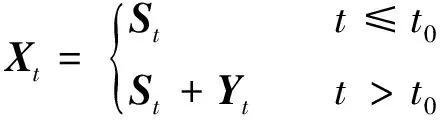
(9)
当出现跳跃时,Yt为常数;当出现趋势时,Yt为时间t的函数,可用最小二乘法拟合求得。
据年最大洪峰流量序列非一致性检验结果,肯斯瓦特控制流域1957—2006年年最大洪峰流量序列在变异点1993年前后可分为2个子序列,即1957—1993年为第1个子序列,其均值为321.220 m3/s;1994—2006年为第2个子序列,其均值为507.846 m3/s。2个子序列的均值差为186.626 m3/s,即为确定性跳跃成分。由此可得出肯斯瓦特控制流域年最大洪峰流量序列的跳跃成分为

(10)
根据线性叠加原理Xt=St+Yt,可得到年最大洪峰流量序列的随机性成分为
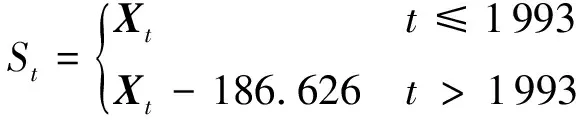
(11)
据此可求得肯斯瓦特控制流域1957—2006年年最大洪峰流量序列剔除跳跃成分后的随机序列。此序列为过去条件下年最大洪峰流量序列,受气候变化和人类活动影响小,能满足水文时间序列的一致性要求。
3.2 序列合成计算
假设过去条件下年最大洪峰流量序列服从P-Ⅲ型分布,采用优化适线法[27]可得过去条件下年最大洪峰流量序列统计参数均值E=321.22 m3/s、变差系数Cv=0.51、偏态系数Cs=2.30,拟合效率系数R2=91.53%。根据其统计特征,采用Monte Carlo随机模拟生成法,可生成500个随机性成分Sp,并结合t时刻(2006年)确定性跳跃成分Yt,利用数值合成公式可得:
Xt,p=Yt+Sp
(12)
由式(12)可得现状条件下(2006年)年最大洪峰流量序列的样本点据,通过优化适线法对其进行P-Ⅲ型分布拟合,得到现状条件下年最大洪峰流量序列统计参数E=507.85 m3/s、Cv=0.32、Cs=2.28、R2=97.95%。玛纳斯河肯斯瓦特水库防洪规划、过去条件和现状条件下相应频率的融雪洪水设计值见表2。

表2 年最大洪峰流量序列不同时期的设计值
由表2可以看出,随着设计洪水重现期的减小,肯斯瓦特水库的防洪规划、过去条件和现状条件下相应频率的设计洪水均减小。根据邹全等[28]的研究成果可知,肯斯瓦特水库控制流域降水量呈波动减少趋势,而气温则呈显著上升趋势。过去条件下与防洪规划时相比,设计洪水均减小了,其减小的变化量在增大,这主要与该流域降水量呈下降趋势有关。现状条件下与防洪规划时相比,设计洪水均增大了,其增大的变化量在增大,虽然上游存在不合理的放牧等人类活动,但其影响相对较少,主要是受到该流域气温呈显著上升趋势的影响,使设计洪水量增大。
4 肯斯瓦特水库极限防洪风险率分析
随着全球气候变暖和人类活动对流域下垫面的干预加剧,融雪洪水时间序列已发生变异,而肯斯瓦特水库的规划设计是以传统的计算理论和方法为基础,这显然与实际情况不符,一旦发生水文极端事件,可能会威胁水库及下游保护区的安全。再加之现状条件下肯斯瓦特水库年最大洪峰流量相应频率的设计值比规划值均存在不同程度的增大,但在现有的水库调度运行规则下,肯斯瓦特水库防洪调度的极限防洪风险率必将增大,为了确保水库的安全,发挥水库最大的综合效益,需要对其极限防洪风险率进行进一步的量化研究。
4.1 极限防洪风险率定义
在确保水库大坝及下游防洪保护对象安全的前提下,水库调度运行中,选取一个极限风险控制指标Zd(校核洪水位、设计洪水位或坝顶高程等特征水位),将汛期限制水位Z0作为调洪演算的起始水位,以不同频率设计洪水过程线的不同时段设计洪水作为入库流量,进行调洪演算,当某一频率洪水的调洪最高水位Zm等于或高于极限防洪风险指标Zd,则此频率称为该指标Zd在汛限水位Z0下的水库极限防洪风险率Pf[29],可通过下式计算:
Pf=P(Zm≥Zd)
(13)
4.2 极限防洪风险率计算方法
近年来,许多国内外学者对这方面的问题做了大量的研究,提出了一些计算极限防洪风险的方法,主要有频率分析法、随机微分方程法、随机模拟法。本文选择频率分析法对肯斯瓦特水库的过去、现状两种条件下不同频率的设计融雪洪水值分别进行水库极限防洪风险率计算。频率分析法是发展最早、最简单的一种方法。该方法假定水库年调洪最高水位与年最大洪水出现的频率相同,以年调洪最高水位等于或高于不破坏水利工程极限指标水位的洪水频率作为水库极限风险率。具体的计算步骤为:首先指定一个水库极限防洪风险控制指标Zd,计算出不同设计频率Pi(i=1,2,…,l)下入库设计洪水过程,然后根据起调水位Z0,并结合水库防洪调度规则进行调洪演算,通过不断的试算,计算出l个最高库水位Zmi(i=1,2,…,l),最后建立Zmi~Pi经验频率曲线,并依据此频率曲线可由Zd值反查出水库极限防洪风险率Pf。
4.3 肯斯瓦特水库调洪演算
肯斯瓦特水库防洪标准为500年一遇洪水设计,5 000年一遇洪水校核,校核洪水位为993.35 m,坝顶高程为996.6 m。校核洪水位是水库在非正常运用情况下,临时允许达到的最高洪水位。若水库的水位超过校核洪水位时,则认为此水位威胁到了水库安全,因此本文选取肯斯瓦特水库校核洪水位(Zd=993.35 m)作为极限防洪风险的控制指标,汛限水位(Z0=984 m)为起调水位。此时,肯斯瓦特水库的极限防洪风险即为其校核防洪风险。
4.3.1水库调洪规则
通过河道过流能力分析,结合防洪工程的总体布局,从防洪要求的角度出发,考虑以水库水位结合下游泄量500 m3/s为控制条件进行调洪演算,其规则为:
a. 当入库洪水小于50年一遇的标准时,水库水位低于防洪高水位992.66 m,控制水库的洪水下泄,最大下泄洪水为500 m3/s。
b. 当入库洪水大于50年一遇标准时,水库运行按照水库水位分时段控制。当入库洪水小于下游安全泄量500 m3/s时,来多少泄多少,维持水库汛限水位984 m不变。当水库水位低于防洪高水位992.66 m时,若入库洪水大于下游安全泄量500 m3/s,下泄量不超过下游安全泄量500 m3/s。当水库水位超过防洪高水位992.66 m时,若入库洪水流量小于泄洪建筑物下泄能力,按入库洪水流量下泄,维持防洪高水位;若入库洪水流量超过泄洪建筑物下泄能力时,根据泄洪建筑物的泄流能力自由下泄。退水段水位逐渐下降至汛限水位后,若入库洪水流量小于泄洪建筑物泄流能力,则维持汛限水位不变;若入库洪水流量大于泄洪建筑物泄流能力,则根据泄洪建筑物的泄流能力自由下泄。
4.3.2水库调洪成果
以1996年典型融雪洪水过程为基础,通过同倍比缩放法得到过去、现状两种条件下不同频率设计融雪洪水过程,并作为入库融雪洪水,根据水库水位-库容-泄量关系曲线,结合肯斯瓦特水库调度运行规则,经调洪演算,分别得到两种设计洪水条件下的调洪成果,见表3。图3和图4分别给出了过去和现状两种条件下5 000年一遇、1 000年一遇、500年一遇及50年一遇设计洪水过程调洪演算得到的库水位变化过程和下泄流量过程。
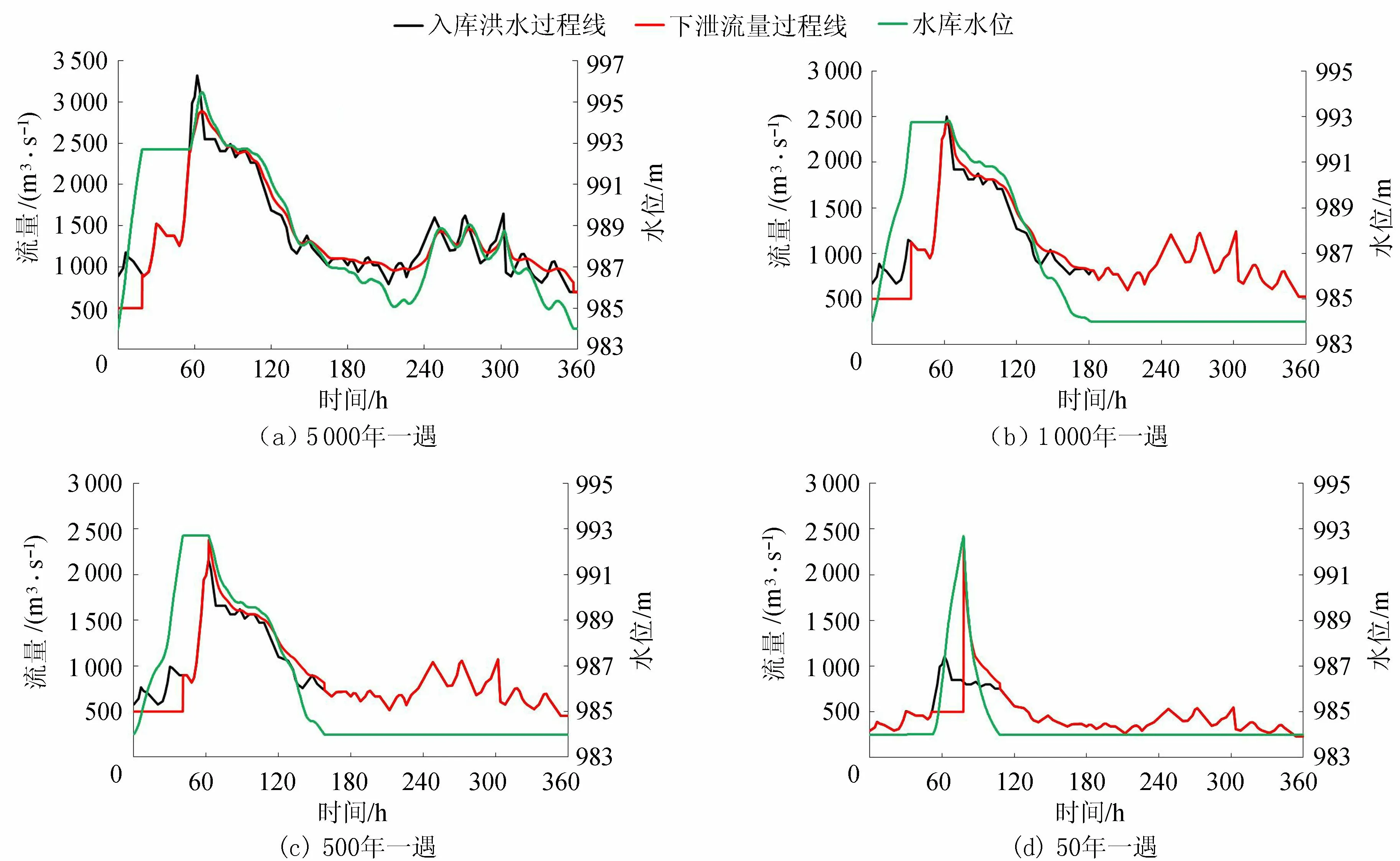
图3 过去条件下不同重现期洪水对应的库水位和下泄流量过程线
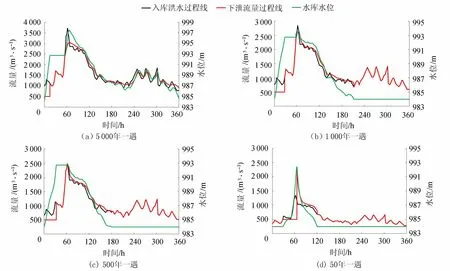
图4 现状条件下不同重现期洪水对应的库水位和下泄流量过程线

表3 肯斯瓦特水库调洪成果
4.4 肯斯瓦特水库极限防洪风险率
根据肯斯瓦特水库调洪演算结果,得到过去和现状两种条件下不同设计频率(重现期)所对应的汛期最高库水位如表3所示。根据表3,分别建立过去、现状两种条件下的最高库水位与设计频率之间的相关关系,即Zm~P经验频率曲线如图5所示,并依据此频率曲线可由Zd值反查出水库极限防洪风险率Pf。
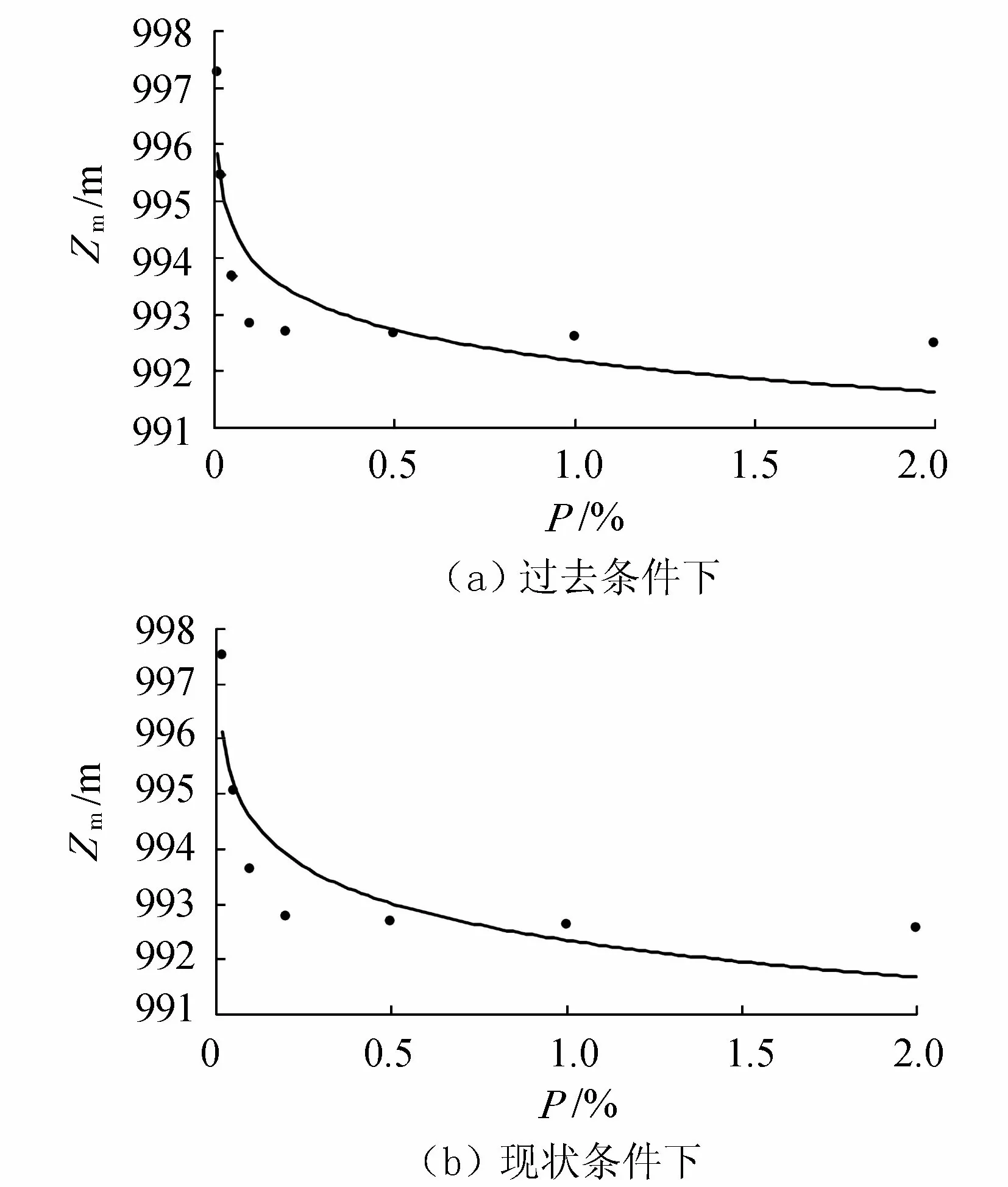
图5 水位频率曲线
从表3可知,过去条件下肯斯瓦特水库0.02%设计频率所对应的最高库水位Zm=995.48 m,根据水库校核洪水位Zd=993.35 m,由图5(a)可查得水库极限防洪风险率Pf=0.231 23%>0.02%;而现状条件下肯斯瓦特水库0.02%设计频率所对应的最高库水位Zm=997.51 m,其水库极限防洪风险率Pf=0.354 58%>0.02%。这说明肯斯瓦特水库控制流域气温、降雨量以及融雪洪水径流量的变化,导致水库极限防洪风险在过去、现状条件下均有所增大,而现状条件下水库极限防洪风险相对于过去条件来说也有所增大。其主要原因在于虽然肯斯瓦特水库控制流域人类活动干预较少,流域降雨量呈减少的趋势,但是流域气温呈显著上升趋势,温度升高引起以冰雪融水为基础的融雪洪水径流的季节性变化,改变了流域降水、融雪洪水径流的时空分布和原有产汇流过程,使融雪洪水径流过程产生变化,造成融雪洪水特征序列的变异,使得肯斯瓦特水库控制流域年最大洪峰流量序列呈增加的趋势。根据肯斯瓦特水库调洪演算结果,由表3可知,水库在遭遇5 000年一遇(频率0.02%)设计洪水时,过去条件和现状条件下的最大泄量分别为2 887.36 m3/s和3 056.30 m3/s,两种情况下最大泄量均略大于校核洪水位时最大泄量设计值(2 596 m3/s),这也为肯斯瓦特水库实施动态汛限水位控制,充分利用汛期洪水资源及提高水库综合效益提供了客观条件。
5 结 论
a. 肯斯瓦特水库年最大洪峰流量序列在1993年发生变异;序列整体上升趋势不显著,在1957—1993年子序列呈显著下降趋势,而1994—2006年子序列变化趋势不显著;序列趋势成分效率系数为6.38%,跳跃成分效率系数1993年为23.09%,跳跃变异为序列主要的变异形式。结合物理成因分析可知,序列发生变异的主要原因为气候变化,最可能的变异点1993年是合理可靠的。
b. 采用“分解-合成”理论对跳跃变异的年最大洪峰流量序列进行一致性修正,得到过去条件下年最大洪峰流量序列的统计参数E=321.22 m3/s、Cv=0.51、Cs=2.30;而现状条件下E=507.85 m3/s、Cv=0.32、Cs=2.28。结合优化适线法进行P-Ⅲ型分布拟合,将得到的相应设计频率下还原、还现年最大洪峰流量设计值分别与防洪规划设计值对比分析,过去条件下设计洪水值均减小了,减小的变化量在增大,而现状条件下设计洪水值均增大了,并且增大的变化量也在增大。
c. 以1996年典型融雪洪水过程为基础,通过倍比缩放法得到过去、现状两种条件下不同频率设计融雪洪水过程,并作为入库融雪洪水,根据水库水位-库容-泄量关系曲线,结合肯斯瓦特水库调度运行规则,经调洪演算,分别得到两种设计洪水条件下水库坝前最高库水位。以校核洪水位(Zd=993.35 m)作为水库极限防洪风险控制指标,采用频率分析法进行分析计算,过去条件下肯斯瓦特水库极限防洪风险率Pf为0.231 23%,而现状条件下其极限防洪风险率Pf为0.354 58%,两种条件下复核后的肯斯瓦特水库极限防洪风险率均大于5 000年一遇的校核标准(0.02%)。
