长方形和正方形病例诊治

□封国云

马小虎在学习长方形和正方形时的作业中出现了不少差错，现在我们来帮他纠错吧。

［病例1］判断：对边相等的四边形一定是长方形。（ ）

［病症］（ √ ）。

［诊断］“病症”错在没有理解长方形的特征。长方形不仅对边相等，而且四个角都是直角。对边相等的四边形不一定是长方形，也可能是正方形，还可能是平行四边形（如下图）。

［处方］（ × ）。

［病例2］判断：长方形是一种特殊的正方形。（ ）

［病症］（ √ ）。

［诊断］“病症”错在没有理解正方形与长方形之间的关系。长方形具有的所有特征（对边相等，四个角都是直角）正方形都具有，而正方形四条边都相等的特征长方形不具有。因此我们应说，正方形是一种特殊的长方形。

［处方］（ × ）。

［病例3］判断：下面两个图形的周长不相等。（ ）

［病症］（ √ ）。

［诊断］“病症”错在没能正确理解周长的含义。封闭图形一周的长度，是它的周长，可见图形的周长是指围成一个图形的所有边线的总和。左图是一个不规则图形，我们若把其中的红色线段和蓝色线段向右平移至图中的位置（如下图），粉色线段和绿色线段向上平移至图中的位置，原图形的周长就可以转化成长方形的周长，可见病例中两个图形的周长是相等的。

［处方］（ × ）。

［病例4］解决问题：把两个长都是6 厘米、宽都是4 厘米的小长方形拼成一个大长方形，大长方形的周长是多少？

［病症］（6+4）×2＝20（厘米），20×2＝40（厘米）。

［诊断］“病症”错在没能正确理解长方形周长的含义，误以为拼成的大长方形的周长等于两个同样的小长方形的周长之和，而不知道拼成的大长方形的周长比两个小长方形的周长之和少了两条宽（如下图）。

［处方］方法1：先求出一个小长方形的周长为（6+4）×2＝20（厘米），再求出两个同样的小长方形周长之和为20×2＝40（厘米），最后用两个小长方形的周长之和减去两条宽的长度，就可求出拼成的大长方形的周长为40-4×2＝32（厘米）。

方法2：先求出大长方形的长为6×2＝12（厘米），再求出大长方形的周长为（12+4）×2＝32（厘米）。

［病例5］选择：用24 张边长是1 厘米的正方形纸拼成一个长方形，这个长方形的周长最短是（ ）厘米。

A.50 B.20 C.24 D.22

［病症］（ C ）。

［诊断］“病症”错在没有弄清共有几种不同的拼法，也不清楚在什么情况下拼成的长方形周长最短。把24 张边长1 厘米的正方形纸拼成一个长方形，共有4 种不同拼法，不同拼法的周长如下表所示：

?

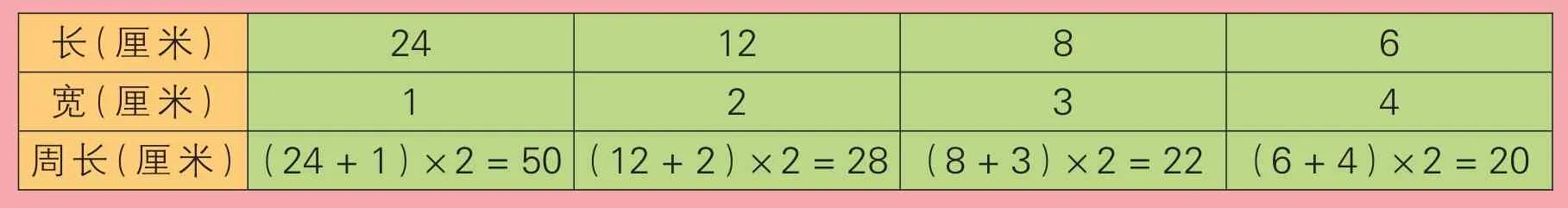
通过上面的计算，可以看出长方形的周长最短是20 厘米。观察上表中的数据，我们可以发现：在所用正方形的总个数不变的前提下，长和宽相差得越小，长方形的周长就越小；长和宽相差得越大，长方形的周长就越大。

［处方］（ B ）。

小朋友，马小虎的错误你都看出来了吗？类似的错误你可不能再犯哦！