冰致海上风电基础结构稳态振动分析
2019-12-25王帅飞张大勇王国军孙星宇王刚于东玮2岳前进
王帅飞,张大勇,王国军,孙星宇,王刚,于东玮2,岳前进
(1.大连理工大学 海洋科学与技术学院,辽宁 盘锦 124221;2.大连船舶重工集团海洋工程有限公司,辽宁 大连 116000)
冰致结构的稳态振动是直立海洋工程结构上最危险的冰激振动形式[1-3]。
基于现场实测数据的分析,冰速在0.02~0.04 m/s范围内,海洋平台结构会发生稳态振动,并且在稳态振动过程存在频率锁定现象[4]。通过对灯塔(见图1)在2001—2003年期间监测到的响应数据的分析,灯塔发生共振响应时冰厚集中在0.26~1.90 m之间,冰速一般在0.023~0.075 m/s之间,但很少发生稳态振动[5]。由于现场监测数据的缺乏,目前还没有从现场实测数据监测到海上风电发生稳态振动的情况。海上风电与海上石油平台、灯塔等海洋工程结构的结构特性有一定的区别(见表1),相比于海上石油平台及灯塔,海上风电更高、更柔,属于一种高耸柔性细长结构。因此,不能根据海上平台及灯塔的振动响应情况来说明海上风机基础结构是否会发生稳态振动。海冰与柔性结构发生破碎的能量谱频率多数集中在0~1 Hz之间,使得海上风电结构固有频率和挤压交变冰力的频率范围很接近,在与冰作用过程中,结构振动的动力效应会比较明显。海冰是否会引发海上风电基础结构稳态振动,考虑用理论计算及数值模拟两种方法进行预判。

图1 海上工程结构
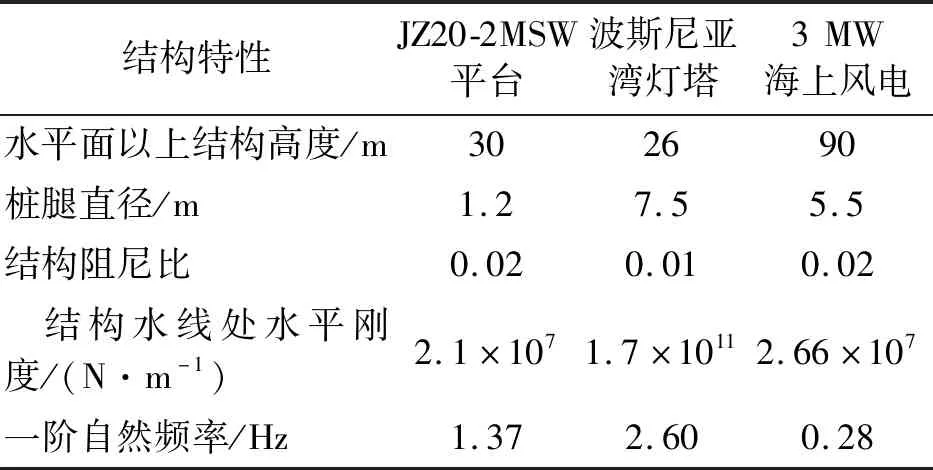
表1 几种典型海上工程结构的结构特性对比
1 风电基础结构稳态振动分析
1.1 冰厚
ISO19906(2010)中给出了评估结构不同振型对频率锁定敏感性的经验公式(A.8-69)。基于某海上单立柱风机基础现场实测数据分析,得到海上风电基础结构的阻尼比约为0.02。根据原型结构建立ANSYS有限元模型,风机基础为单桩形式,风机塔筒结构模型采用shell181单元,风机机头采用MASS21质量单元模拟,泥面以下基础采用6倍桩径法建立,即泥面以下基础长度为基础直径的6倍,底部固定约束。冰力作用位置为坐标原点所处高度的塔筒结构,见图2。

图2 风机基础的有限元模型
对结构进行模态分析,结果见表2,与原型结构基频一致,有限元模型能够反应真实风机结构的动力特性。

表2 风机频率
ISO19906(2010)指出冰荷载频率通常会与结构低阶频率发生频率锁定,在此计算风电基础前两阶频率是否会发生频率锁定,提取结构模态质量Mn,计算参数见表3。

表3 风机结构计算参数
由式(A.8-69)可得,冰厚大于0.04 m时,风机基础结构可能在一阶频率下发生频率锁定现象;冰厚大于0.041 m时,风机基础结构可能在二阶频率下发生频率锁定现象。根据以上对前两阶频率的讨论,冰厚大于0.04 m时,风机基础结构有可能出现稳态振动,发生频率锁定现象。
1.2 冰速
海冰的力学性质随冰速改变会明显变化,在低冰速下,冰的破坏强度与弹性模量随应变速率增加,海冰以韧性破坏为主;随着冰速增加到一定值,冰强度达到最大,此时冰处于韧脆转变点处;随后随着冰速增加冰强度减小,海冰以脆性破坏为主。稳态振动则发生在冰从韧性破坏到脆性破坏转变的过度区,即韧脆转变阶段[6-7]。对于引起结构发生稳态振动时冰速的条件,一些文献和规范提出了几种方法来估算可以产生频率锁定的最大速度。
ISO19906(2010)提出了公式(A.8-71)。
文献[8]等基于实验及全尺寸观测,给出了估算频率锁定最大冰速的公式。
(1)
根据《中国海海冰条件及应用规定》冰的弹性模量E取值为1.0~3.0 GPa;Kn为结构n阶模态单自由度系统刚度,N/m。
文献[9]利用冰板应变速率经验公式及Karna的研究工作,给出了计算直立结构稳态振动上限冰速的公式。
Vmax=0.9dεeq
(2)
式中:εeq=10-2s-1
文献[10]给出了以下公式。
Vmax=αfnh
(3)
式中:α取值0.01~0.40;h为冰厚,m。
对于此风机冰作用处基础直径d为5.5 m,由以上各式计算得到稳态振动的上限冰速结果见表4。其中,文献[8]公式计算结果与其他计算结果差异很大,理论计算结果有待进一步验证。

表4 基于分析方法估算频率锁定的最大冰速
2 基于离散元的数值模拟分析
2.1 主要模型参数
结合离散元软件主要对几种冰速下海上风机基础结构的振动模式进行讨论。冰荷载的激励能量随冰厚的上升而上升,海上风电属于高耸柔性结构,冰厚越大,结构更容易出现稳态振动过程[18-19],采用渤海50年一遇冰厚0.4 m作为计算冰厚,冰速分别为0.02、0.04、0.08 m/s,模型参数见表5。
2.2 不同冰况下结构振动模式分析
通过离散元模拟得到,在冰厚0.4 m,冰速0.02 m/s的冰况下,冰力加载缓慢,风机基础响应的动力效应不明显,此时接近于静冰力过程,结构为准静态振动模式。 见图3。
在冰厚0.4 m,冰速0.04 m/s的冰况下,通过离散元模拟300 s时长,见图4。
截取其中55~75 s时间段的结构响应,将结构动位移和冰力放到同一时间轴上,见图5。

表5 海冰与风机直立结构作用离散单元模拟的主要计算参数

图3 冰厚0.4 m、冰速0.02 m/s冰况下冰力时程及结构动位移

图4 冰厚0.4 m、冰速0.04 m/s冰况下冰力时程及结构动位移
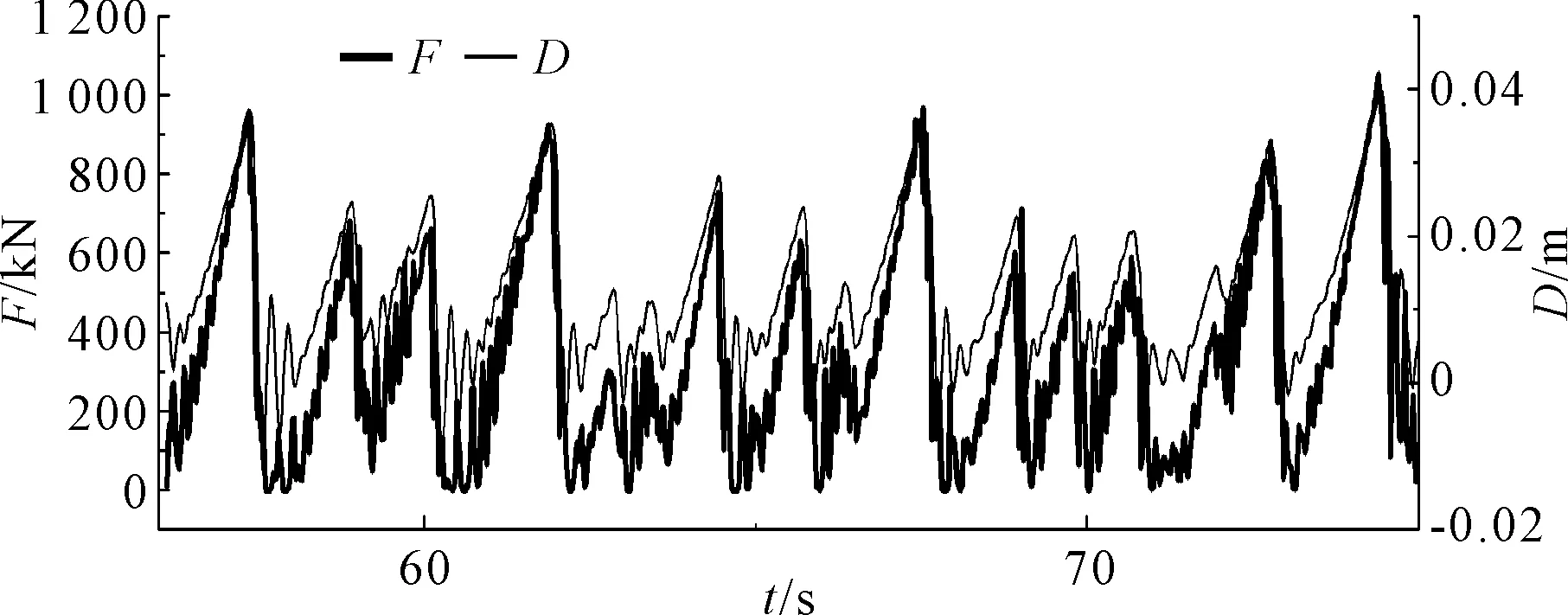
图5 冰力和结构动位移的耦合
可以看到冰力和结构振动发生频率锁定现象,此时激励频率接近结构固有频率,结构振动表现为类似简谐运动的稳态振动形式,此时冰的破坏进入韧脆转换阶段[11]。海冰与结构作用的破坏过程模拟见图6。

图6 海冰与直立结构作用的挤压破碎过程
图6a)可知,在韧性破坏阶段,单元失效次数没有随着逐渐增加的冰载荷而增多,结构前的海冰维持一定的堆积高度;由6b)到6c)可知,随着加载速率增大,单元粘结失效次数逐渐增加,海冰堆积高度增加,海冰此时处于韧脆转换阶段。到图6d)阶段单元粘结失效次数保持较高水平,结构处于回弹阶段,结构与海冰相对速度迅速增大,海冰发生脆性破坏。
在冰厚0.4 m,冰速0.08 m/s的冰况下,通过离散元模拟得到冰力时程和结构振动位移,从时程上看都呈现不规则的随机变化,见图7。

图7 冰厚0.4 m、冰速0.08 m/s结构冰力时程及振动响应
离散元数值模拟结果见表6。
海上风机基础结构在低冰速下会发生准静态振动;随着冰速增加到0.04 m/s左右,会发生稳态振动,出现冰力和结构振动的频率锁定现象;在较快冰速下结构会发生随机振动。结合理论计算结果,数值模拟与式(A.8-71)、式(2)、式(3)计算得到的稳态振动冰速都在0~0.05 m/s范围内,而与式(1)计算结果有很大差异,故海上风机基础结构可能会在冰速小于0.05 m/s的范围内发生稳态振动。

表6 离散元模拟的各冰况下出现的挤压冰力模式
3 稳态振动概率分析
通过整理分析渤海石油平台多年来的海冰监测数据,得出海冰冰厚的概率密度函数为[20]
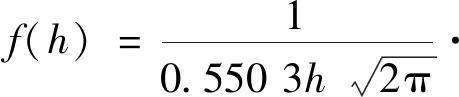
(4)
式中:h为海冰厚度。
冰速的概率函数为
(5)
式中:v为海冰速度。
根据水文参数,采用冰厚0.04~0.30 m,以0.05 m为间隔,冰速0.05~0.80 m/s,0.1 m/s为间隔,共54种工况进行计算。根据式(4)与式(5)计算得到冰速与冰厚的联合概率分布见表7。
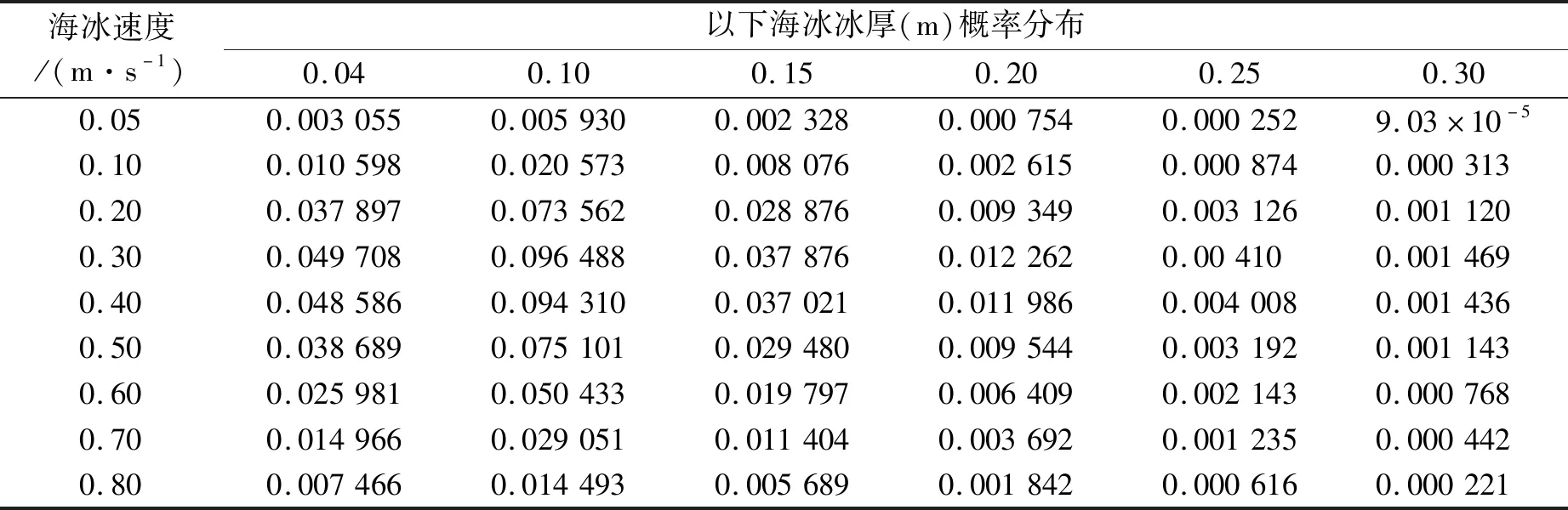
表7 冰况的发生概率
由以上分析可得可能引发海上风机基础结构稳态振动的条件(冰厚0.04 m及以上,冰速0.05 m/s以下)的冰况出现的概率约为1.246%,考虑到其中包含有发生非稳态振动的冰况,得到的概率值为保守估计,说明发生稳态振动的概率很小。
4 结论
1)利用理论公式计算及离散元数值模拟,得到海上风机基础结构可能会在冰厚0.04 m以上,冰速小于0.05 m/s的冰况范围内发生稳态振动。
2)依据渤海海域冰厚冰速分布概率经验公式,得到海上风机基础结构可能会出现稳态振动的概率约为1.246%,说明稳态振动及频率锁定现象出现的概率很低。
对寒区海上风机基础结构发生稳态振动的问题用理论及数值模拟的方法进行分析,可为海上风机基础结构进行合理化的抗冰振设计提供参考,下一步需要基于现场实测数据对海上风机基础结构稳态振动的发生进行分析。
