关键是“如何从条件想起”

王九红

【关键词】解决问题的策略;从条件想起;空间能力;联系;思维

【中图分类号】G623.5  【文献标志码】A  【文章编号】1005-6009（2019）81-0049-04

《解决问题的策略：从条件想起》是苏教版三上的内容，是苏教版教材“解决问题的策略”系列内容的起始安排。在学习这一内容之前，学生对“从条件想起”的做法已经有很多经验积累，如在四则运算时，两个数相加（或减、乘、除）就可以求出和（或差、积、商）;在解决一、两步计算的实际问题时，利用已知条件可以求出未知问题。从学生学习的实际情况看，要解决问题就需要已知条件，这已被学生视为理所当然，而利用已知条件去解决问题的做法已成为学生自然而然的行为。因此，此内容的教学重点不在于让学生知道“从条件想问题”这个方法，而在于向学生明确提出“策略”的概念，促进其形成自觉运用“从条件想问题”策略的意识。更关键的，是要让学生通过解决实际问题学会一些从条件想起的具体方法。

【教学过程】

一、铺引

师：果园里的桃子熟了，小猴帮妈妈摘桃，他摘桃的本领越来越强。你瞧！（课件出示图1）同学们，从中你们知道了些什么？

（图1）

生：我知道小猴第一天摘了30个桃，还知道他以后每天都比前一天多摘5个。

师：你知道的这些信息在解答问题时叫什么啊？（板书：条件）利用条件可以求出什么？（板书：问题）根据这些条件，你能提出哪些问题？

生：第二天摘多少个桃？第三天摘多少个桃？第四天摘多少个桃？第五天摘多少个桃？    两天一共摘多少个桃？……

师：看来大家还可以提出更多问题，我们来选两个，（课件出示：小猴第三天摘了多少个？第五天呢？）你们能解答出这些问题吗？

这一环节自然地引出“条件”和“问题”的概念，激活了学生从条件想问题的已有经验，为学生学习从条件想问题这一解决问题的策略做了铺垫。

二、探究

1.理解数量关系。

师：要解答数学题，首先要读题目。题目的意思你们都能理解吗？哪儿比较难理解？

生：以后每天都比前一天多摘5个。

师：你是怎么理解这句话的？

生1：第二天比第一天多摘5个，第三天比第二天多摘5个……

生2：第一天摘的个数加5就是第二天摘的个数，第二天摘的个数加5就是第三天……

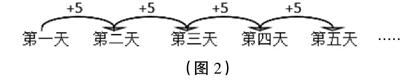
教师在黑板上画箭头表示（如图2）。

（图2）

师：这句话还可以怎么理解？

生3：第三天比第一天多摘5+5个，第四天比第一天多摘5+5+5个，第五天比第一天多摘5+5+5+5个。

师：第六天比第一天多摘多少个？第七天呢？

生4：第六天比第一天多摘5个5，第七天比第一天多摘6个5，第n天比第一天多摘（n-1）个5。

师：你真厉害！字母n都用上了。刚才大家都在和第一天相比，能不能和别的天数相比再说说呢？

生5：第三天比第二天多摘5个，第四天比第二天多摘5+5个。

生6：第五天比第二天多摘15个，比第三天多摘10个……

师：大家说得很多了，但好像都是一种类型的，谁能说出一个和以上都不同的说法？

生7：第一天比第二天少摘5个，比第三天少摘10个……

师：你的反应真快！这是逆向思维。大家看看，“以后每天都比前一天多摘5个”这句话可以正着说，也可以反着说，根据它还可以变化出许多说法，这些说法说得完吗？

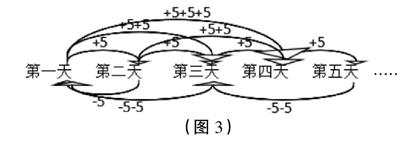
教师根据学生的发言在黑板上画箭头表示（如图3）。

（图3）

师：其实，任意两天之间都有相差的数量关系，在数学中表示相互关系都可以换一种方式来说。

理解题意是问题解决首要且必然要做的事。题目中有许多信息，要想成功解题就必须弄清楚那些不明白的信息（条件），抓住那些重要的信息（条件）。题目中最难理解的是“以后每天都比前一天多摘5个”这句话，这句话概括了许多数量关系，它是解题的关键。本环节，教师大胆放手，通过引发学生对“以后每天都比前一天多摘5个”这句话的多种理解，使学生的思维不断走向深入和开阔。

2.运用关系解题。

师：同学们，你们打算怎样解题？

学生在随堂本上解答，教师巡视，相机指导，并挑选学生的作业，按照以下顺序（如下页图4）展示：

3.解释解题方法。

师：我们先来看看这三位同学的解答，你们能看懂吗？

…………

师：张明的做法大家都看懂了，是一步一步地求出第二、三、四、五天摘桃的个数。那后面两种做法呢？我们先请李伟俊同学来解释一下自己的解法。

李伟俊：因为第二天比第一天多摘5，第三天又比第二天多摘5个，所以第三天比第一天多摘两个5个，就是10个，所以第三天就是30加10个，等于40个。

师（指着“10+10”）：这求的是什么？

李伟俊：第三天比第一天多一个10，第五天比第三天又多一个10，所以第五天比第一天多两个10，就是20，第五天就是30加20，等于50个。

师：现在大家能看懂杨阳同学的解法了吧？

在教學中，教师要相信学生，启发学生开动脑筋，让他们“跳一跳，摘桃子”，因而本环节教师没有让学生按照课本上指定的分步法和填表法解答。前面已经让学生充分理解了“以后每天都比前一天多摘5个”的含义，并用多种数量及其关系进行了等价表达，所以学生自然地利用不同的关系找到了不同的解题办法。第一种解法比较简单，不需要解释;第二种解法有点难度，要让学生解释，接受大家的质疑;第三种解法和第二种解法相似，可以不再多说。

4.归纳解题策略。

师：这些不同的解法有什么相同之处？

生：答案相同;都用到30和5这两个条件。

师：是啊，如果答案不同就说明我们的解答至少有一个错了。回头看看这道题的解答过程，你有什么体会？

生：要弄清题目中每个条件的含义，看清要求的问题;（板书：理解题意）要从条件开始想起，确定先算什么，再算什么;（板书：分析关系）可以列式计算，也可以列表找出答案。（板书：列式解答）

师：像这样，从已知条件出发分析和解决问题，是一种常用的解决实际问题的策略。（板书：解决问题的策略：从条件想起）“策略”一词是什么意思？对，大概就是方法的意思，希望同学们在今后解决问题时能主动运用这种从条件想起的策略。

“解决问题的策略”内容是学生第一次遇到，学生对“策略”一词的理解也不尽相同，所以要强调一下，让学生大略了解其意。

三、练习

1.根据图5中的已知条件提出不同的问题，并说说怎样解答。

师（指砝码）：知道这是什么吗？（砝码）对，砝码是用来称重量的。从图中你知道了哪些条件？根据这些条件你可以提出什么问题？

生：1个苹果多少克？1个橙子多少克？1个苹果和1个橙子共重多少克？

师：谁能说说如何来解答这三个问题？

生：根据4个苹果和500克这两个条件可以求出1个苹果的克数，再根据“1个橙子比1个苹果重20克”可以求出1个橙子的克数，把它们加起来就是1个苹果和1个橙子一共的重量。

学生说，教师板书（如下页图6）：

教师相机指出：1个苹果的重量原来不知道，是要求的问题，它被求出来后就可以作为已知条件了，它和“1个橙子比1个苹果重20克”合起来就可以求出1个橙子的重量。同样，求出来的1个橙子的重量也可以作为条件来利用。凡是已经求出来的问题都可以作为条件来利用。

…………

这道题是用图形来表征条件的，是对学生文字题意理解方式的扩展。只给了条件而没有给出问题，目的是促使学生自觉地从条件去想问题。让学生说解答方法，就是强化学生从条件想问题的思维方式。教师用树形图直观形象地呈现了学生的思维过程，着重说明了求出来的问题可以转化为条件，让学生感受到解题的过程就是从较少的已知条件出发不断求出未知问题，进而将其视为条件再求出新的问题的持续累积过程。

2.出示一些关于学校社团的信息：（1）科技社团有5个班;（2）科技社团每个班有12人;（3）数学社团人数是科技社团的一半;（4）舞蹈社团比科技社团少16人;（5）科技社团共有33名女生。

师：同学们，如果让你们将这5个条件分成两类，你怎么分？标准是什么？

生：（1）（2）（5）分为一类，它们都只讲了科技社团;（3）（4）分为一类，它们不仅讲了科技社团，还讲了数学和舞蹈社团。

师：说得太好了，（1）（2）（5）三个条件中都只有一个对象，就是科技社团，而（3）（4）两个条件中都有两个对象，像这种表示两个对象之间关系的条件叫作关系条件。关系条件在解题中非常重要，解题时一定要将关系条件找出来，理解清楚。（板书：关系）

这是一道开放题，有多种选择条件的方式，有助于学生有效地体会和巩固从条件想起的策略。同時，可以促进学生发散思维，培养他们思维的灵活性和求异品质。

【教后反思】

本节课，教师抓住《解决问题的策略：从条件想起》一课的重点，将精力主要放在让学生学习、掌握“从条件想起”策略的具体方法上。具体而言，就是紧扣题目中的关系条件展开教学，抓关系—变关系—用关系构成了本节课的主线。

1.抓关系。

数学是研究数量关系和空间形式的科学。空间形式在某种意义上也可以看成各个数学对象在空间上的相互关系，从这个角度说，数学也可以看成研究关系的科学。数学知识可以形象地视为众多数学对象构成的关系网络，数学问题就是由一些特定的数学对象连接成的关系“局域网”，只不过其中的一些数学对象我们已经知晓，还有一些目前还不知道。知晓的是条件，不知道的叫问题，解题就是利用条件顺着关系的线索去弄明白问题。从问题解决的角度看，题目中的条件可以分为两类，一类是单纯刻画数学对象某种属性的条件，课中练习第2题中的（1）（2）（5）即属于此类;另一类是描述两个或多个数学对象之间关系的条件，可以称为关系条件，课中练习第2题中的（3）（4）就属于此类条件。既然关系条件是连接不同数学对象的桥梁，因而循着恰当的关系条件可以成功解决问题。因此，解决问题时就要重点关注关系条件。

2.变关系。

数学关系是复杂多样的，有的比较直观，有的比较抽象，有的简单直接，有的复杂曲折;其表征方式也是多样的，有文字的，有符号的，还有图形的表征，抑或三者兼而有之。从解题教学的角度看，就是要帮助学生找出隐晦的条件，弄明白复杂的条件，理清楚杂乱的条件，具体方法包括动作演示、画示意图、转换表达等。本节课中，教师抓住题目中“以后每天都比前一天多摘5个”这个关系条件鼓励学生尽量多地“换一种说法”，不仅可以促进学生深刻理解题意，也为他们打开了多个解题通道。将题目中呈现出的关系进行另一种方式的表征，其实质是一种寻找从条件通向问题桥梁的行为，在问题解决的教学中，教师要多进行这种“换一种说法”的训练，促进学生形成转化关系的思维习惯。

3.用关系。

不是所有的关系都有利用价值，要成功解题就要找到那些有用的关系。有用的关系就是一头连着已知条件一头连着未知问题的关系。运用不同的关系就会走上不同的前进通道，形成不同的解题方式方法。本节课的例题教学，教师放手让学生进行充分的关系变化，多样化的关系表达为解题方法的多样化提供了坚实的基础。在练习第2题中，不同的关系条件连接着不同的数量条件和问题，使要解决的问题具有开放性，能有效地帮助学生由关系去想问题解决策略的形成。■

（作者单位：南京市天正小学）