飞机水平放置拱形端盖圆柱油箱动态油量计算模型研究

李向明　李玉芳

摘要：通过对不同姿态情况下飞机水平放置的拱形端盖圆柱油箱内油面相对油箱的位置变化情况进行系统详尽分析，按油面与油箱之间的不同关系分情况建立油箱油量计算模型，给出不同姿态下的实时显示油量与实际油量之理论差值。

Abstract：  Based on the system and exhaustive analysis of the position change of the hydraulic oil surface relative to the hydraulic oil tank in the horizontal placement cylindrical tank with arch end cap under different attitude conditions， the hydraulic oil volume calculation model of the tank is established according to the different relationship between the hydraulic oil surface and the hydraulic oil tank， and the theoretical difference between the real-time display hydraulic oil volume and the actual hydraulic oil volume under different attitude conditions is given.

关键词：油箱;高度;油量;坡度;计算模型

Key words： oil tank;height;oil volume;falling gradient;calculation model

中图分类号：V228.1+2                                    文献标识码：A                                  文章编号：1006-4311（2019）35-0267-04

0  引言

飞机液压油箱用于储存液压油、液压油在飞机正常飞行过程中基本不消耗，但是其油量为实时显示。为准确了解油箱显示油量与实际油量之间的差值，对油箱内液压油面随飞机姿态变化之后相对于油箱的位置变化情况进行分析，给出了二者不同关系情况下的油箱油量计算模型，应用计算模型计算获取不同姿态情况下油箱内实时显示油量与实际油量之间的差值，大大提升油箱H-V曲线计算速率。

1  概述

飞机液压油箱一般采用带拱形端盖的圆柱形油箱，采用柱面回转中心与翼展方向平行的方式安装，一般油箱较小，因此，为减少油箱内油量测量显示误差，一般将其安装在飞机对称平面或靠近对称面处，传感器亦安装在油箱中间，以便满足飞机俯仰和滚转时油量测量误差相对较小的要求。其油箱与传感器的布局见图1。

2  油箱H-V曲线分析

为保证计算模型的通用性和简便性，对带拱形端盖的圆柱形油箱，根据保容原理，需将拱形端盖简化为容积相等的圆柱形，如图2，将油箱G-H-F-K-J-C-G简化为G1-H1-K1-J1- G1。

根据油箱水平安装特性，油箱半径R，油量传感器浸油高度H，简化后油箱长度（高度）b，图2中油面AB对应的圆心半角为θ，则水平安装的圆柱油箱的H-V曲线为弓形截面A-B-S-A与简化油箱高度b的乘积，其数学计算模型为：

θ=arccos（（R-H）/R）（1）

V= b×（π×θ×R2/180-R2sin（2×π×θ/180）/2）/1000000

（2）

公式（1）中：

b，R，H，单位：mm;

θ单位：°;

V单位：L 。

3  油面位置及油量计算模型研究

油箱作为飞机结构的一部分，随飞机的加减速、俯仰、偏航和滚转而产生自身姿态的变化，但在加减速过程完成后，不考虑油箱油面波动影响情况下，油面受重力作用的影響始终平行于地面，根据这个情况，对油箱俯仰情况和倾斜情况油面与油箱的相互关系进行分析研究，建立油量计算模型。

3.1 俯仰变化

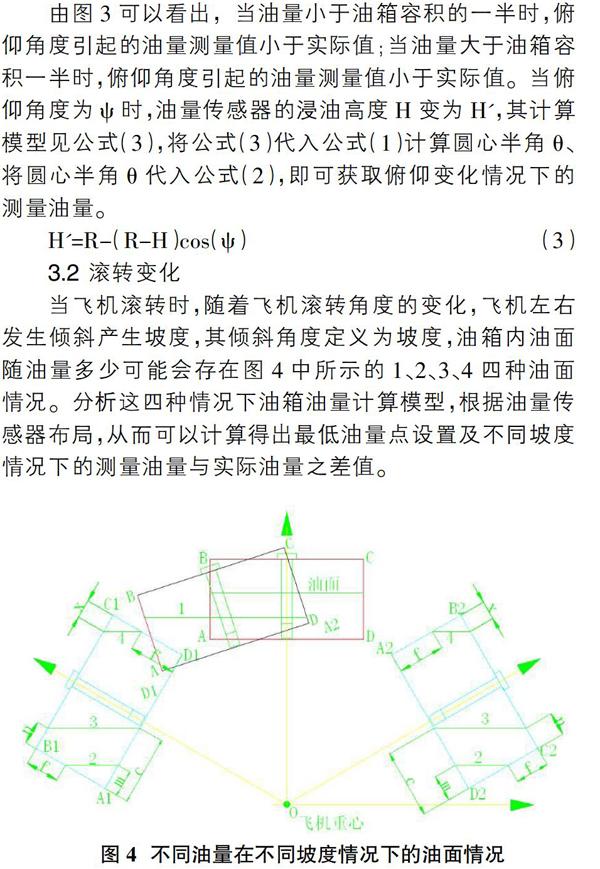
刹车油箱为圆柱形，沿翼展方向水平安装，油量测量传感器安装在中轴面上，不管俯仰角度如何变化，油箱内实际油面高度不会发生变化，但油量测量传感器的浸油高度会随俯仰角度变化而变化，俯仰角度变化引起的油量测量值与实际油量值之间的变化趋势大小与油量传感器浸油高度的变化相关，见图3。

由图3可以看出，当油量小于油箱容积的一半时，俯仰角度引起的油量测量值小于实际值;当油量大于油箱容积一半时，俯仰角度引起的油量测量值小于实际值。当俯仰角度为ψ时，油量传感器的浸油高度H变为H'，其计算模型见公式（3），将公式（3）代入公式（1）计算圆心半角θ、将圆心半角θ代入公式（2），即可获取俯仰变化情况下的测量油量。

H'=R-（R-H）cos（ψ）（3）

3.2 滚转变化

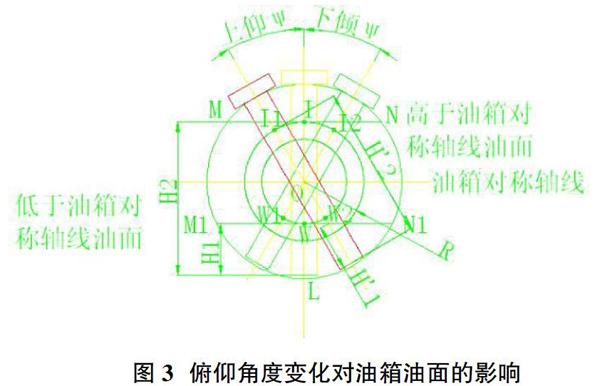
当飞机滚转时，随着飞机滚转角度的变化，飞机左右发生倾斜产生坡度，其倾斜角度定义为坡度，油箱内油面随油量多少可能会存在图4中所示的1、2、3、4四种油面情况。分析这四种情况下油箱油量计算模型，根据油量传感器布局，从而可以计算得出最低油量点设置及不同坡度情况下的测量油量与实际油量之差值。

飞机坡度角为γ，油箱长度或高度b，底圆半径R，油面在上圆柱表面的高度为n，在下圆柱表面的高度为c或m，当油面未没过下圆底面上顶点时，在下圆底面上，上顶点至浸油处的距离为f。当油面没过上圆底面下顶点时，在上圆底面上，下顶点至浸油处的距离为f。圆柱下底面未浸油弧长对应中心角的半角为？准。

当油面处于图4所示油面位置1时，油面未没过下圆底面上顶点同时也未过上圆底面下顶点，此时油量计算分析图见图5。当油面处于图4所示油面位置2时，油面未没过下圆底面上顶点和上圆底面下顶点，此时油量计算分析图见图6（顺时针转90°）。

由图4、图5、图6计算不同坡度下油箱内油料的油量值，建立不同坡度情况下油箱油量的理论计算模型。

tanγ=（2R-f）/m=2R/b=2R/（c-n）（4）

式中（见图4）：

γ—坡度（倾斜角），单位°;

R—底圆半径，单位mm;

b—油箱高度或长度，单位mm;

m、c—圆柱下表面浸油高度，单位mm;

n—圆柱上表面浸油高度，单位mm。

当油面倾斜，油面未没过下圆底面上顶点也未没过上圆底面下顶点时，见图6，利用积分方法可得油量计算数学模型：

V=cR3[sin？准+（π-？准）cos？准-sin3？准/3] /（2R-f）（5）

式中（见图6）：

c—圆柱下表面浸油高度，单位mm;

？准—圆柱下底面未浸油弧长对应中心角的一半，单位mm;

R—底圆半径，单位mm;

f—下圆底面浸油弦至下圆底面上上顶点距离，单位mm;

V—油料体积，单位L。

当油面没过下圆底面上顶点但未没过上圆底面下顶点时：

V=πnR2+πR2（c-n）/2（6）

式中（见图4）：

R—底圆半径，单位mm;

n—圆柱上表面浸油高度，单位mm;

c—圆柱下表面浸油高度，单位mm。

当油面没过下圆底面上顶点和上圆底面下顶点时（参考图6）：

V=πHR2-cR3[sin？准+（π-？准）cos？准-sin3？准/3] /（2R-f）（7）

式中：

H—圆柱高度，单位mm;

c—圆柱上表面未浸油高度，单位mm;

？准—圆柱上底面浸油弧长对应中心角的一半，单位°;

R—底圆半径，单位mm;

f—上圆底面上浸油弦至上圆底面下顶点距离，单位mm;

V—油料体积，单位L。

当油面未没过下圆底面上顶点但已没过上圆底面下顶点时（参考图5），浸油体积为下圆底面浸油圆缺对应的圆缺柱体积与上圆底面浸油圆缺对应的圆缺柱体积之和的一半：

V=bR2 （（π×θ1/180-sin（π×θ1/90）/2）+（π×θ2/180-sin（2π×θ2/180）/2））/2/105（8）

式中：

b—圆柱高度，单位mm;

θ1—圆柱上底面浸油弧长对应中心角的一半，单位°;

θ2—圆柱下底面浸油弧长对应中心角的一半，单位°;

R—底圆半径，单位mm;

V—油料体积，单位L。

3.3 偏航变化

飞机偏航时，飞机前行方向发生变化，但油箱油面与油箱之间的关系不受偏航角度的影响。

4  应用实例

以某型机某系统油箱设计为例，油箱直径拟选用300mm，拱形端盖弓高拟设计为37mm，圆柱直线段长度拟采用430mm，通过容积等效后，油箱变为直径300mm，长度580.2mm的圆柱油箱，应用上述计算模型用C++语言编程对不同坡度情况下油箱H-V曲線进行了计算，程序流程图见图7，计算结果见图8，根据油箱出油口布局及飞机常用坡度计算获取低油面告警点为7+1L，按飞机最大坡度90度计算获取低油面告警点不露出的油量需求，见图9，提出油箱加油量不低于22L。以低油面告警点7L和满油量22L分别计算不同俯仰和坡度下的测量油量与实际油量之偏差见图10和图11。

5  结论

通过对不同姿态情况下油箱油面与油箱的相互关系进行详尽系统分析，获取带拱形端盖圆柱油箱的油量与传感器浸油高度（H-V）计算通用数学模型，并利用C++语言编程计算模型解决实际油箱油量设计选取问题，同时，可以在油量测量计算过程中通过与飞机姿态角交联而选用不同的H-V曲线，可以大大提升油箱油量显示误差。

参考文献：

[1]国家技术监督局颁布，JJG266-96卧式金属罐容积，中国计量出版社，1996.

[2]蒋青，王强，等.高等数学[M].七版.高等教育出版社，2014.

[3]楼琪.飞机油量指示不正常的故障分析[J].价值工程，2015，34（25）：83-84.