基于EDEM的地下铲运机铲装过程仿真研究

严 勃，战 凯，郭 鑫，李恒通，石潇杰

(1.北京矿冶科技集团有限公司，北京100160；2.北矿机电科技有限责任公司，北京100160)

地下铲运机铲装过程中的铲斗受力情况不方便直接获取，为了对铲装过程中铲斗受到的铲装阻力有一个更加直观的认识，铲装阻力的计算一直是研究热点。国内外从30年前就开始对铲装阻力进行研究，经历了从实验中总结的经验公式的阶段，利用散体力学和土压力理论的理论计算阶段，和现阶段的计算机数值模拟计算阶段。本文利用EDEM软件完成地下铲运机的铲装过程中铲装阻力的计算。

1 仿真模型

为了方便建立仿真模型，这里做出如下假设：将矿石块体用球形颗粒代替，矿石粒径用球半径表征，修正摩擦系数补偿球形颗粒与块状颗粒的差异；颗粒之间无粘连无挤压破坏。

仿真模型需要解决以下三个问题：

1)矿石尺寸问题，矿石的尺寸决定仿真颗粒的尺寸，决定了仿真的可靠性；

2)铲斗模型，铲斗模型决定了铲装过程中接触力的变化；

3)铲斗运动轨迹，EDEM软件只提供有限的运动方式，不同的运动对铲装阻力影响很大。

1.1 矿石尺寸分布的确定

在描述矿石爆破后的块度分度时常用的函数有高斯分布、对数正态分布、泊松分布、伽玛分布和Rozin-Rammler分布。文献资料表明，对地下矿山爆破，常使用Rozin-Rammler分布和对数正态分布表征矿石分布情况。

Rozin-Rammler分布函数为：

(1)

对数正态分布函数为：

(2)

式中：y—通过筛孔尺寸的百分比；x—矿石尺寸；xo—矿石特征尺寸，反映矿石的块度或者粗细程度。

查阅文献可知对于一次爆破后的矿石块度分布情况，对数正态分布适用于细颗粒部分的分布，Rozin-Rammler分布则适用于粗颗粒部分的分布，单一的分布不能完整描述矿石的分布。EDEM软件提供四种分布方式:固定分布、对数正态分布、随机分布与正态分布。为了完整的描述爆破后矿石粗细的分布，本文选用正态分布[1]。

根据铲装能力，矿石块度分布最大尺寸lmax计算公式如下：

式中：E—铲运机铲斗容量。

借用块体形状系数来描述矿石块体形状，γ—矿石的实际体积，v-与以矿石最大尺寸为直径的球体体积的比率[2]。

(3)

根据上述公式可得矿石的等效半径R计算公式。

(4)

从参考文献中获取爆破岩石的块体形状系数，γj。由上式可以计算得到等效半径R=0.05～0.217 m。

当选择矿石颗粒半径R=0.15 m为正态分布均值μ时，此时的矿石实际尺寸可按如下公式计算为

查阅文献得爆破后的矿石属性如下表1所示。表中的参数均是查阅文献得到，文献中的料堆颗粒也是爆破岩石，具有一定的参考性。这里对岩石密度做一定调整，适应金属矿山的爆破矿石。表1中的摩擦系数为矿石的自摩擦系数。

表1 矿石属性参数

1.2 铲斗模型的确定

铲斗的模型从CAD中导入，然后选择铲斗的属性，这里采用如表 2 铲斗的属性参数。摩擦系数为钢与矿石的摩擦系数。

表2 铲斗属性参数

然后，选择模型的接触模型。EDEM软件提供四种接触模型。Hertz-Mindlin(no-slip)接触模型，这是软件默认模型。Hertz-Mindlin模型，常见于适合岩石结构和混凝土的仿真研究。Hertz-Mindlin热传导模型，常见于密相颗粒流的仿真研究。线性接触模型，分为线性粘结接触模型和线性弹簧接触模型。对于大部分颗粒材料，使用非线性接触模型能更贴合实际地反映颗粒间的作用力和变形、碰撞速度的变化关系。综合考虑后，为提高计算效率，本文采用EDEM默认接触模型Hertz-Mindlin(no-slip)。

2 仿真过程

准备工作做好后，第一步是形成矿石料堆。这里利用EDEM软件的Factory工厂生成矿石颗粒并形成料堆。首先建立一个几何体，作为采场空间，几何体选用Box模型，设定好尺寸，选择属性为实体，材料属性为矿石，取消Box的顶面与正面，顶面产生矿石颗粒，正面是铲斗的作业空间。然后利用Factory工厂在Box顶面产生矿石，并自由落体形成料堆，这时矿石会产生滑动，形成斜坡。料堆如下图 1所示。

图1 矿石料堆模型Fig.1 Ore heap model

给铲斗加载一定的运动驱动。首先是铲斗铲入矿石料堆，然后是铲斗铲装矿石，最后是退出矿石料堆。这里的铲斗轨迹不能像MATLAB中一种准确的控制，EDEM软件值提供三种运动驱动方式:直线平移旋转、正弦平移旋转、传送带平移旋转[3-5]。因此这里采用直线平移旋转。首先是铲斗平移前进铲入料堆一定深度，然后铲斗翻转举升，在前文中铲斗应该是由动臂油缸和转斗油缸的驱动函数进行复合运动控制，这里采用旋转运动来近似铲斗铲尖的运动轨迹，用圆弧代替二次函数曲线，在模拟铲装过程中，铲斗的运动形态如图 2所示。

图2 铲装过程的铲斗状态Fig.2 Bucket state in shovel loading process

3 试验结果

图 3 、图4和图 5 表征仿真结果，为铲斗在铲装过程中受到的总力在X、Y、Z三个方向的分力随时间的变化关系。其中横轴起点50表示开始铲装时间，60表示铲装结束，铲运机开始后退，单位s；纵轴表示各方向所受铲装阻力的大小。

图3 铲装阻力的X轴分力Fig.3 X-Axis component of scraping resistance

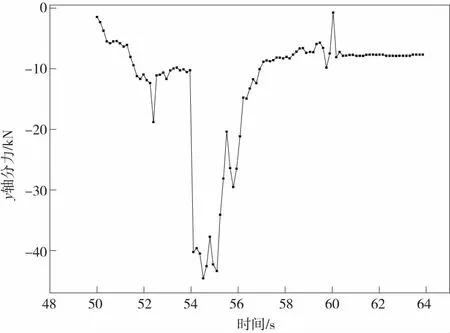
图4 铲装阻力的Y轴分力Fig.4 Y-Axis component of scraping resistance

图5 铲装阻力的Z轴分力Fig.5 Z-Axis component of scraping resistance

铲装过程中铲斗所受切向铲装阻力与法向铲装阻力变化曲线，如图 6所示。

图6 铲装阻力的切向分力和法向分力Fig.6 Tangential and normal components of loading resistance

在相同参数条件下，多次进行仿真模拟，记录其最大铲装阻力出现的时间，以及此时的最大X轴铲装阻力和最大Y轴铲装阻力、铲装深度，具体数据如表 3所示。

表3 铲装仿真结果数据表

从表3中可以看到铲装阻力的X轴分力最大值和Y轴分力最大值在54.5 s左右出现，即在铲斗从铲入阶段向铲取阶段转变的时间；这个时间，铲斗产生铲取作用，对矿石料堆有一个挤压和剪切，X轴分力产生突变；铲斗产生一个沿Y轴的加速度，所以Y轴分力出现突变。

4 结论

本文利用EDEM离散学软件，对地下铲运机铲装过程进行了仿真分析，得到了铲装阻力曲线。在铲入阶段，铲装阻力与铲入深度成正比；在进入铲取阶段的时刻，铲装阻力激增达到70 kN，这是因为要克服巨大的剪切阻力；进入铲取阶段后，铲装阻力又下降，因为这个阶段的剪切阻力减小。对实现铲运机自主铲装功能有一定的指导意义。