浅埋地下爆炸的地面运动研究
2019-12-24张伟艾广建陈仁山
张伟,艾广建,陈仁山
(1.山东交通学院交通土建工程学院,山东济南 250357;2.山东泰山路桥工程公司,山东泰安 271000;3.山东交通学院道路安全中心,山东济南 250357)
0 引言
经过久远的地质年代,在内力和外力共同作用下,岩体上形成了无数裂隙,方向不同,形状各异。在工程地质特性上,裂隙的存在使岩体内部结构不均匀、不连续,在物质的构成成分、强度和密度等方面表现出差异性。浅理地下爆炸与定向爆破、预裂爆破、微差控制爆破、拆除爆破、燃烧剂爆破不同,具有瞬时性、多变性。因此,预测爆破地震波在岩体中的传播运动规律,为爆破振动灾害预测提供理论基础等研究工作面临诸多复杂的、不可控因素,内容涉及爆炸力学、弹性动力学、非线性有限元理论、岩石力学与工程、结构工程、地下工程等多学科知识,难度较大[1-3]。
自20世纪以来,国内外学者依据爆炸力学、岩石动力学等基本理论知识,现场观测获取大量爆破振动数据,并利用有限元或离散元等分析软件建立网格实体模型,模拟分析爆破振动过程,研究爆破地震波的传播规律、爆破振动安全判据和爆破振动灾害预测,取得的成果在爆破地震理论和工程应用领域有重要的指导意义。但是,由于爆破的瞬时性、多变性和所处岩体介质的复杂性,爆破振动的随机性很大。随着爆破工程数量的增多和工作面的增广,特别是人们环保意识日益增强,早期的研究成果已不能满足现代爆破振动安全预测的需求[4-6]。
本文研究岩石中浅埋地下爆炸的地面运动响应问题。根据爆炸等效荷载模型,将爆炸源简化,建立浅埋地下爆炸作用下地震波传播的计算模型,并结合爆破实例,运用MATLAB语言编程进行实例计算分析,定量分析浅埋地下爆炸的地面运动规律。
1 浅埋地下爆炸的模型
1.1 计算模型

O—简化模型的球心;P0—来自震源的纵波;P1—来自自由表面的反射波;S1—由反射波P1所引起的横波;ρ—材料密度;λ,μ—拉梅系数;R0—破坏半径;Wz—垂直位移;Wr—水平位移;r—当前位置半径。图1 浅埋地下爆炸的等效模型
基于弹性动力学和爆炸力学理论,采用Sharpe提出的等效孔穴理论和等效荷载模型,将浅埋地下爆炸的震源等效为半径为R0的球形空腔,震源距自由表面为H,即震源埋深为H,对浅埋地下爆炸的地表运动进行研究,如图1所示[7-8]。
等效荷载模型将震源视为整个球形模型的破坏区,破坏区的运动特征参数决定弹性区中爆破地震波的传播运动过程。
1.2 基本理论
在弹性半空间介质中,纵波速度及横波速度分别为Cp、Cs。
在地下爆炸波的传播过程中,用破坏区表面的径向粒子速度表示震源函数,即:
ur=u0f(t),
式中:u0为常数,t为时间,f(t)为关于时间的函数。
基于弹性动力学的理论知识,利用空间球对称运动,采用线性波动方程对爆破地震波的传播问题进行求解。
假设浅埋地下爆炸的初始状态为简化模型的球心,介质中质点的径向位移w可以表示为[9-11]:
球形计算过程中,用势函数表示介质中质点的径向位移
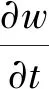
(1)
式中:R为空腔半径,Φ(ξ)为势函数。
当t=0时,对式(1)积分得:
(2)
式(2)对R求导得质点位移
(3)
式(3)对t求微分,得粒子的速度
用Φ0(ξ)表示R=R0球面上的集中源脉冲,即:
在圆柱坐标下,浅埋爆炸震源在z轴负方向上引起的地面运动位移
,
式中:r为爆心距;z为观察点的坐标;k、J0为圆柱坐标系下函数进行拉普拉斯变换的常量;i为常量。
1.3 浅埋地下爆炸的响应计算模型
将浅埋地下爆炸的震源等效为一个球形空腔,采用弹性动力学中的经典Lama解,对水平方向和垂直方向形成的位移场进行研究。在自由表面上,水平方向的位移用wr表示,垂直方向的位移用wz表示[12-14],任意扰动作用下,地表位移
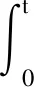
(4)
基本集中震源的爆破动态响应函数用f1(t-τ)表示,时间函数平移后则有
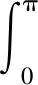
(5)
式中τ*从爆炸过程的起爆时刻开始算起。
基本脉冲扰动下,地表位移wε(r,z,t)在水平方向的分量
wεh=w0ε+wRε+wλε,
(6)
在竖直方向的分量
(7)
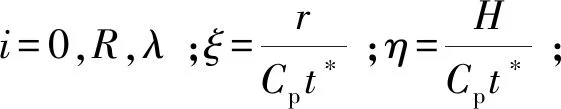
球坐标系下位移量的其他两个分量[15-17]为:
(8)
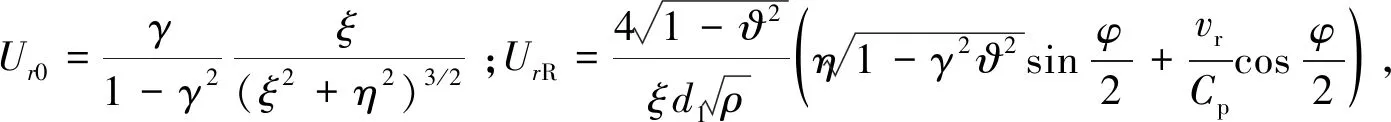
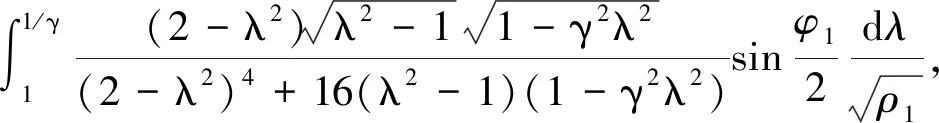
式(4)~(8)为浅埋地下爆炸的研究模型,根据研究模型计算水平方向的地表位移和垂直方向的地表位移,从而确定岩石中浅埋地下爆炸作用下地面的位移场,研究地面运动的响应。
2 工程实例计算与分析
某爆破工程为青岛市经济技术开发区的一个大型水库扩容爆破施工监测项目。该爆破区的基岩大部分为微风化岩石(花岗岩),岩体比较完整,无明显的节理和断层带。该次爆破采用TNT炸药,炸药的密度为1500 kg/m3,炸药的爆轰速度为3800 m/s,装药半径为0.05 m,孔距为1.5 m,孔深为2.2 m,排距为1.1 m。花岗岩密度ρ0=2650 kg/m3,泊松比v=0.3,弹性模量E=62 GPa,纵波波速为4600 m/s。取炸药TNT质量为200 kg进行计算分析,装药半径Rd=0.05 m。
为研究岩石中浅埋地下爆炸的地面运动响应,在爆破现场对爆破震动进行实时的跟踪监测工作。根据式(4)~(11),采用MATLAB编制实体模型程序,模拟不同爆心距和不同震源埋深处爆破地震波的水平运动和垂直运动,求解不同条件水平运动的位移响应和垂直运动的位移响应[18-23]。
选取爆心距r为2R0与8R0,选择震源埋深H为R0、2R0与3R0进行模拟计算。不同条件下水平、垂直运动位移响应ωH、ωV的模拟计算结果如图2~4所示。
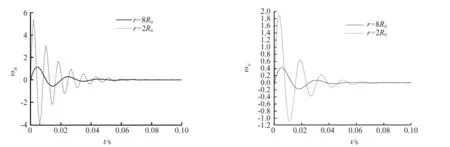
a)水平运动 b)垂直运动图2 H=R0的运动响应

a)水平运动 b)垂直运动图3 H=2R0的运动响应
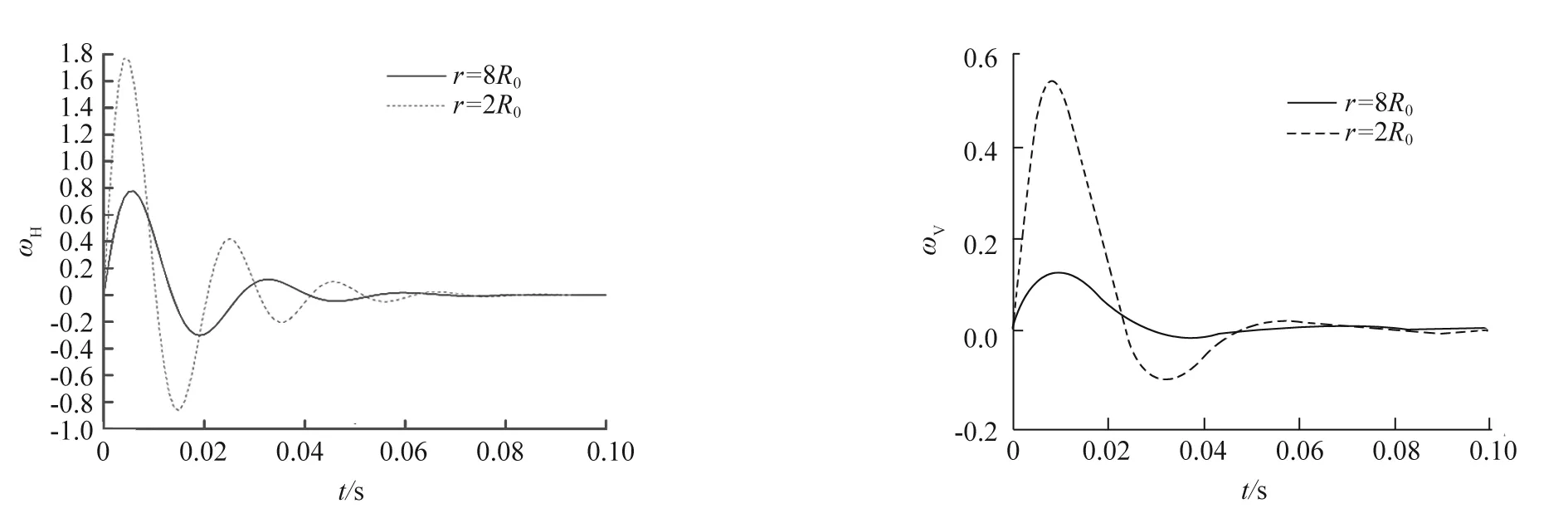
a)水平运动 b)垂直运动图4 H=3R0的运动响应
由图2~4可知:沿爆心距方向,随着爆源距离的减少,地面测点水平方向和垂直方向的位移响应增加;在震源埋深保持不变时,垂直方向的位移随传播距离的增加而减小。采用MATLAB自行编制的实体模型程序确定不同爆心距和不同震源埋深处的水平运动和垂直运动,直观给出了爆破地震波的传播过程。
与现场的爆破振动监测数据进行对比,模型程序计算得到的地面运动响应运动与实际数据变化规律一致,验证了所建研究模型的可行性。
3 结论
爆破具有瞬时性、多变性加之所处岩体介质较为复杂,因此爆破振动的随机性很大。运用自行编制的基于MATLAB的实体模型程序,结合爆破动力学的基本理论,模拟岩石中浅埋地下爆炸的地面运动响应。
1)根据浅埋地下爆炸的简化模型,建立浅埋地下爆炸的响应计算模型,在研究爆破作用下的地面运动方面具有方法简单高效、结果可靠等特殊优势。
2)实体模型程序详细模拟了不同爆心距和不同震源埋深处的水平运动和垂直运动响应,直观给出了爆破地震波的传播过程,分析模拟计算结果并进一步结合工程实例,将确定的地面运动响应与现场的爆破振动监测数据进行对比,验证了所建研究模型的可行性。
3)基于MATLAB的实体模型程序可以优化爆破设计方案,为爆破振动灾害预测提供了可靠理论基础。
