联合动力学与运动学的汽车状态估计
2019-12-24肖川
肖川
(长安大学汽车学院,陕西西安 710064)
0 引言
随着汽车技术的发展,汽车主动安全装置越来越多,需要已知汽车的纵向速度、横向速度、横摆角速度及质心侧偏角[1-6],由于直接测量这些参数成本太高,一般采用滤波方法[7]和观测器方法[8],利用容易测量的状态量估算出难以测量的状态量。Yue 等[9]利用无迹卡尔曼滤波估计汽车的纵向速度和横向速度,为底盘的集成控制提供依据;Antonov等[10]利用无迹卡尔曼滤波估计汽车的状态,并进行了实车试验。王震坡[11]等利用自适应无迹卡尔曼滤波对汽车的纵向速度、横向速度以及质心侧偏角进行了估计,但文中使用的是线性轮胎模型,当轮胎侧偏角超过5 ℃时,轮胎会表现出非线性特性,导致横向力估计不准,从而导致状态估计误差较大;张家旭等[12]采用基于交互式多模型和容积卡尔曼滤波(cubature kalman filter,CKF)估计,由于采用了3个交互式模型,导致计算量较大,不利于实时状态估计,但该方法与容积卡尔曼滤波相比提高了精度。张凤娇等[13]用蚁群算法对无迹卡尔曼滤波进行优化,与传统无迹卡尔曼滤波相比,精度略有提高,计算量依旧较大。在汽车运行状态的观测中对横向速度估计常常存在较大的偏差。李克强等[14]采用汽车动力学和运动学相结合的汽车状态融合估计方法,准确地估计了汽车在多种典型运行状态下的横向速度,但它需要额外的GPS传感器,在实际应用中会导致成本增加,不利于大规模应用。
相对于容积卡尔曼滤波,球面单形径向容积卡尔曼滤波(spherical simplex-radial cubature kalman filter,SSRCKF)采样点更多,估计精度更高[15]。采用基于汽车动力学模型的SSRCKF滤波器,并以汽车纵向加速度、横向加速度、横摆角速度为滤波器量测输入,估计汽车的纵向速度、横向速度及质心侧偏角,此方法对横向速度的估计误差较大,而对汽车的纵向速度估计精度很高。本文采用基于汽车运动学方程的容积卡尔曼滤波,并以SSRCKF估计得到的汽车纵向速度作为容积卡尔曼滤波的量测输入,估计汽车的横向速度,拟提高基于单一模型的汽车横向速度估计精度,从而提高整个汽车状态的估计精度。
1 汽车动力学模型
利用SSRCKF估计汽车的行驶状态,需要汽车的动力学模型。在汽车行驶中,最重要的状态量是纵向速度、侧向速度、质心侧偏角及横摆角速度。复杂的汽车动力学模型使滤波器的响应速度变差,计算量大。常用的七自由度汽车模型,在汽车的状态估计中应用十分广泛,包括汽车的纵向运动、横向运动、横摆运动及4个轮胎的旋转运动,忽略汽车车身的垂直运动、俯仰运动、侧倾运动和轮胎的垂直运动等,能够充分反映汽车的运动特性,计算量小。
1.1 整车动力学模型
汽车动力学模型如图1所示。

图1 车辆动力学模型示意图
汽车运动的微分方程
mdux/dt=(Fx1+Fx2)cosδ-(Fy1+Fy1)sinδ+Fx3+Fx4+mωuy,
(1)
mduy/dt=(Fx1+Fx2)sinδ-(Fy1+Fy2)cosδ+Fy3+Fy4+mωux,
(2)
式中:m为汽车总质量,Izz为车身绕z轴的转动惯量。
1.2 非线性轮胎模型
在汽车的状态估计中,一般采用线性轮胎模型,优点是计算量小,该模型在轮胎的线性范围内较准确,但在非线性范围内与轮胎的实际情况差异较大。常见的魔术轮胎模型[16]能够很好拟合轮胎的各种特性,但需要调整的参数较多,公式也过于复杂。Duoff轮胎模型能够满足轮胎的非线性特性,拟合参数仅有轮胎纵向刚度和侧偏刚度[17],公式为:

式中:μ为地面附着系数;Fz为车轮垂直载荷;εr为拟合系数,一般取0.015;is为车轮滑移率;α为车轮侧偏角;Cx为轮胎纵向刚度;Cy为轮胎侧向刚度;S、f(S)分别为轮胎公式的拟合系数和拟合函数。Fz、is、α等的计算详细见参考文献[18]。
1.3 建立包含噪声的汽车离散化状态方程
记状态向量x=[uxuyω]T=[x1x2x3]T,y=[axayω]T,其中ax为汽车纵向加速度,ay为汽车横向加速度。设采样周期为T,k为采样点。由式(1)~(3)得离散化方程[19]
x1(k+1)=x1(k)+T[(Fx1+Fx2)cosδ-(Fy1+Fy2)sinδ+Fx3+Fx4+mx3(k)x2(k)],
(4)
x2(k+1)=x2(k)+T[(Fx1+Fx2)sinδ+(Fy1+Fy2)cosδ+Fx3+Fx4-mx3(k)x1(k)],
(5)
(6)
式中M=a(Fx1+Fx2)sinδ+a(Fy1+Fy1)cosδ-b(Fy3+Fy4)-[L(Fx1-Fx2)cosδ]/2+[L(Fy1-Fy2)sinδ]/2-L(Fx3-Fx4)/2。
设汽车的过程噪声向量为Nk,汽车的量测噪声向量为Nk′,其协方差矩阵分别记为Qk、Rk,则包含噪声的汽车离散化方程简记为:
x(k+1)=f(x(k))+Nk,
(7)
(8)
式中:x(k+1)=[uxuyω]T;y(k)为x(k)的函数,y(k)=[axayω]T,h、f为式(4)~(6)中函数关系的简化表示。
2 汽车运动学模型
汽车的运动学方程
dux/dt=ax+uyω,
duy/dt=ay+uxω。
汽车运动学方程的状态量
x1=[uxuy]T=[x11x12]T,y1=[ux]T,
离散化得:
x11(k+1)=x11(k)+Tω(ax+x12(k)),
(9)
x12(k+1)=x12(k)+Tω(ay-x11(k)),
(10)
包含噪声的离散化方程简记为:
x1(k+1)=f1(x1(k))+Nk1,
(11)
y1(k+1)=h1(x1(k+1))+Nk1′。
(12)
式中f1、h2为式(9)(10)中函数关系的简化表示。
3 联合滤波算法的迭代过程
在仿真过程中基于汽车运动学方程的CKF中以纵向速度为量测量,但在实际中纵向速度无法直接测量。为解决这一问题,在联合估计算法中以基于汽车动力学方程的SSRCKF估计出的纵向速度作为CKF的量测输入量,以提高汽车横向速度的估计精度。
根据式(7)~(12),假设汽车的ax、ay、ω、δ能够通过传感器测量。以上标r和c分别表示SSRCKF和CKF中的状态量和系数,若不特别指出,其物理含义完全相同,关于滤波算法的详细表述,请参考文献[20]。
3.1 SSRCKF的时间更新
(13)
(14)
(15)
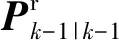
预测值和预测协方差
(16)
(17)
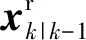
3.2 SSRCKF的量测更新
(18)
(19)
(20)
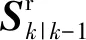
估计测量值及方差计算
(21)
(22)
(23)
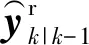
状态估计值及估计状态协方差矩阵
(24)
(25)
(26)
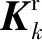
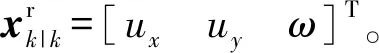
3.3 CKF的时间更新
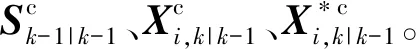
预测值和预测协方差

3.4 CKF量测更新

估计测量值及相差方差计算
状态估计值及估计状态协方差矩阵的更新过程同式(24)~(26)。
4 CarSim和Simulink联合仿真
为了验证联合估计算法,利用CarSim与Simulink进行双移线和连续正弦转向仿真。车辆模型的部分参数为:汽车总质量m=1830 kg,簧上质量ms=1650 kg,Izz=3234 kg·m2,a=1.4 m,b=1.65 m,汽车质心高度h=0.53 m,L=1.60 m,轮胎有效转动半径Re=0.353 m。
假设ax、ay、ω、δ和车轮的角速度[ωc1ωc2ωc3ωc4]可通过传感器测量,使用联合估计算法可估计出汽车的ux、uy。
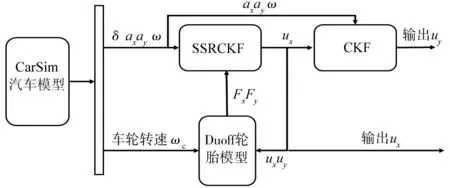
图2 仿真原理图
设置SSRSCKF的过程噪声协方差Qk=diag[100 100 100]T,过程噪声协方差Rk=[1 1 1]T;设置CKF的过程噪声协方差为Qk1=diag[100 100]T,过程噪声协方差为Rk1=[0.001]T;并设2个滤波器的采样时间周期均为T=0.000 5 s。仿真原理图如图2所示。
4.1 连续正弦转向工况
在CarSim中设置汽车在正弦转向工况下运行,汽车的初始纵向速度为120 km/h,μ=0.85;将汽车的ax、ay、ω、δ(由CarSim导出)输入SSRCKF;CKF的量测输入为SSRCKF估计的纵向速度,最后估计出汽车的ux、uy及汽车质心侧偏角β。输入量如图3所示。汽车正弦转向的ux、uy、β如图4~6所示。图4~6中union为联合状态估计值。由图4可知,SSRCKF滤波器对汽车ux估计精度的相对误差为0.3%。图5中联合状态估计的uy精度在峰值处比SSRCKF滤波提高了9.60%。图6中联合状态估计的β精度比SSRCKF滤波提高了8.09%,证明了SSRCKF与CKF联合估计算法的有效性。
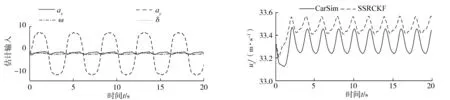
图3 卡尔曼滤波器估计输入曲线 图4 汽车正弦转向纵向速度随时间的变化曲线
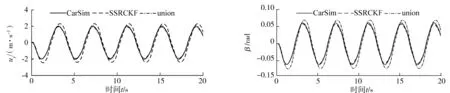
图5 汽车正弦转向工况uy随时间的变化曲线 图6 汽车正弦转向工况β随时间的变化曲线
4.2 双移线试验工况
在CarSim中设置汽车在双移0线工况下行驶,汽车的初始纵向速度为120 km/h,μ=0.85。将ax、ay、ω、δ输入SSRCKF,如图7所示。CKF的量测输入为SSRCKF估计出的纵向速度。
双移线试验工况联合仿真输出结果如图8~10所示。由图8可知,SSRCKF滤波器对ux估计的相对误差为0.24%。由图9、10可知,uy和β联合估计精度分别比SSRCKF提高了4.73%和4.72%。联合估计算法能够快速跟踪纵向速度的变化,提高了估计算法的响应时间,进一步证明了联合估计算法的有效性。

图7 估计输入 图8 汽车双移线试验ux随时间的变化曲线

图9 汽车双移线试验uy随时间的变化曲线 图10 汽车双移线试验β随时间的变化曲线
5 结论
本文采用SSRCKF滤波和CKF滤波,联合汽车的动力学方程和运动学方程对汽车的运动状态进行估计,该算法以基于汽车动力学方程的SSRCKF滤波估计出的纵向速度作为CKF滤波器的输入,再运用CKF滤波和汽车运动学方程估计汽车的横向速度。经联合仿真证明,汽车在正弦转向和双移线工况下,对横向速度的联合估计算法相比SSRCKF滤波分别提高了9.60%和4.73%。
