区域研发投入的循环累积效应估计：2000—2016年

陈 俊

(广东财经大学国民经济研究中心，广东 广州 510320)

0 引言

2000—2016年，中国的研发支出增长迅速，全国研发支出平均每年以16.37%的速度增长，总规模从895.66亿元上升至15676.75亿元，是仅次于美国的全球第二研发大国。在经济新常态下，提高研发投入强度 (研发支出占GDP的比例)已经成为区域发展战略的重要内容。一些经济发达城市，如北京、深圳，2016年研发投入强度已经超过4%，远高于全国平均水平 (约2.11%)。为了更好地反映研发投入对经济增长的贡献，国家统计局已经正式将研发支出纳入GDP核算体系，并制定了 《研究与开发支出计入地区GDP核算方法》。

研发投入对知识产出和技术进步具有重要作用已经成为共识。估计研发投入的经济效应主要有两种范式：第一，在新古典增长模型中引入研发资本 (研发资本一般采用PIM方法测算)，进而估计研发资本对总产出或全要素生产率的贡献[1-2]；第二，以专利、新产品开发等指标作为知识产出的代理变量，研发资本、研发人员等指标作为研发投入，采用新古典生产函数形式估计研发资本对知识产出的贡献[3-4]。这两种范式在本质上没有太大区别，都是将研发投入作为可累积的资本品，将知识生产过程等同于一般的物质生产过程。事实上，知识生产不同于一般的物质生产。在新经济增长理论中，知识生产是一个 “创造性毁灭”的过程。知识既是研发投入的产物，同时又是生产新知识的要素[5-7]。研发投入的作用是不断将旧知识转化为新知识，而新知识又不断地被取代成为旧知识，被取代的旧知识不断累积又成为生产新知识的要素。因此，研发投入与知识产出之间具有一种循环累积因果关系，这一关系对于分析研发投入的经济效应至关重要。

利用2000—2016年省级层面数据，本文在新经济增长理论基础上，首次采用第二代知识生产函数估计研发投入的循环累积效应。研究表明，相比于熊彼特知识生产函数，这期间真实经济更符合琼斯知识生产函数，并且不存在规模效应；使用专利授权量衡量知识产出与使用新产品销售收入衡量知识产出所估计的研发投入循环累积效应存在明显差异，前者比后者更为稳定；这期间中国研发投入的循环累积效应总体上不断增强、区域差异逐步趋于稳定。

1 知识生产过程中的循环累积因果关系

一个区域一旦拥有先发的初始条件，这种优势将不断自我强化，形成一种持续向上或向下的循环累积过程[8]。新经济增长理论可以分为以资本为基础的增长理论和以研发为基础的增长理论[9-11]。在以研发为基础的增长模型中，经济持续增长的动力源于研发投入不断将旧知识转化为新知识，知识生产过程也存在一种如缪尔达尔所说的 “循环累积因果关系”。

1.1 罗默-琼斯知识生产函数

罗默认为，非竞争性和累积性是知识有别于其他商品或要素的两个重要性质[5]。在第一代内生增长模型中，他将新知识表示为关于研发投入和知识存量的函数，表示如下：

ΔAit=λRitσAit-1,0<σ<1

(1)

其中，下标i和t分别表示区域和年份，R表示研发投入，ΔA表示新知识，A表示知识存量。式 (1)不同于新古典框架下的第一代知识生产函数，主要体现在：第一，罗默知识生产函数引入了知识存量，从而刻画的是知识的累积性，而非研发投入的累积性；第二，罗默知识生产函数的研发投入采用流量形式，研发投入通过循环累积的方式不断创造出新知识。

由式 (1)可知，知识产出的增长速度与研发投入规模成正相关 (gA=ΔA/A=λRσ)。这意味着研发投入规模越大，知识产出的增长速度越快，即存在规模效应。琼斯认为，研发投入规模越大，并不一定会导致知识产出增长速度越快[6]。因此，在改进后的半内生增长模型 (Semi-Endogenous Models)中[6,12-13]，知识生产函数表示如下：

(2)

由式 (2)可知，研发难度将随着知识存量的增大而增大，在研发投入保持不变的情况下，知识产出的增长速度将随着知识存量的增大而降低。将式 (2)不断迭代，知识存量表达式如下：

(3)

将式 (3)代入式 (2)，并在等式两边取对数，可得到：

lnΔAit=lnλ+σlnRit+φlnAi0+

(4)

由式 (1)和式 (2)可知，罗默知识生产函数与琼斯知识生产函数的区别主要体现在对φ的假定上，前者假定φ=1，后者假定φ<1。在罗默-琼斯知识生产函数中，新增知识产出由当期研发投入、初始条件和往期研发投入积累共同决定。

本文将研发投入的循环累积效应 (CCE)定义为：除了当期研发投入和初始条件以外，往期研发投入对知识产出的累积贡献。根据式 (4)，罗默-琼斯知识生产函数下CCE的计算公式如下：

lnλ-σlnRit-φlnAi0，0<φ≤1

(5)

1.2 熊彼特知识生产函数

Aghion等[14]和Howitt[7]认为，研发难度将随着市场规模的增大而增大。因此，在知识生产函数中引入了市场规模变量，可得到：

(6)

其中，Q表示市场规模，一般用地区生产总值来衡量，其余变量和参数的定义与式 (2)一致。由式 (6)可知，熊彼特知识生产函数假定知识产出增长速度与研发投入规模成正比，同时与市场规模成反比。同理，将式 (6)不断迭代，知识存量表达式表示如下：

(7)

令研发投入强度sR=R/Q，将式 (7)代入式 (6)，并在等式两边取对数，可得到：

(8)

此时，研发投入的循环累积效应 (CCE)计算公式表示如下：

(9)

1.3 知识生产函数形式的判断方法

根据Ha等[15]的研究，可以将上述三种知识生产函数形式统一表示如下：

(10)

通过检验参数φ、β和σ的值，即可判断知识生产函数的具体形式。如表1所示，给定不同的参数条件，分别可以得到上述三种不同形式的第二代知识生产函数。值得注意的是，琼斯认为，φ< 1 且 0 <β< 1这种混合的半内生增长模型在现实情况中是不存在的[16]。

表1 不同知识生产函数的参数条件

2 第二代知识生产函数的参数估计

根据上述理论分析，在估计研发投入的循环累积效应之前，先要估计出知识生产函数的参数值。在这一部分，本文尝试利用中国省级层面数据分别对罗默-琼斯知识生产函数和熊彼特知识生产函数进行估计，然后根据参数值判断哪种知识生产函数更符合中国真实经济情况。

2.1 计量模型设定

根据式 (10)，在等式的两边同时取自然对数，并引入随机干扰项 (νit)，考虑到知识生产技术的变化，在等式的右边还引入了时间趋势项 (t)，可得到：

lnΔAit=lnλ+σlnRit-σβlnQit+φlnAit-1+t+νit

(11)

式中，新产出知识 (ΔA)用专利授权量 (PAT)和新产品销售收入 (NP)来衡量；R用研发经费内部支出来衡量；市场规模 (Q)用地区生产总值来衡量；知识存量 (A)采用永续盘存法 (PIM)测算，参照白俊红等心测算研发资本存量的办法[17]，折旧率均取15%，基期知识存量 (A0)采用基期知识产出/ (平均增长率+折旧率)。

模型具体估计过程分为两步：第一，施加约束β=0，检验φ是否等于1，判断是否存在规模效应，从而区分罗默知识生产函数和琼斯知识生产函数；第二，施加约束β=1，检验φ是否等于1，从而判断是否支持熊彼特知识生产函数。模型的拟合效果通过对数似然值 (Log-L)进行比较。

本文的研究对象为中国大陆31个省、自治区和直辖市，研究时段为2000—2016年。文中所需数据来自历年 《中国科技统计年鉴》和 《中国统计年鉴》，货币单位统一转换为2000年可比价。各变量的定义及描述性统计如表2所示。

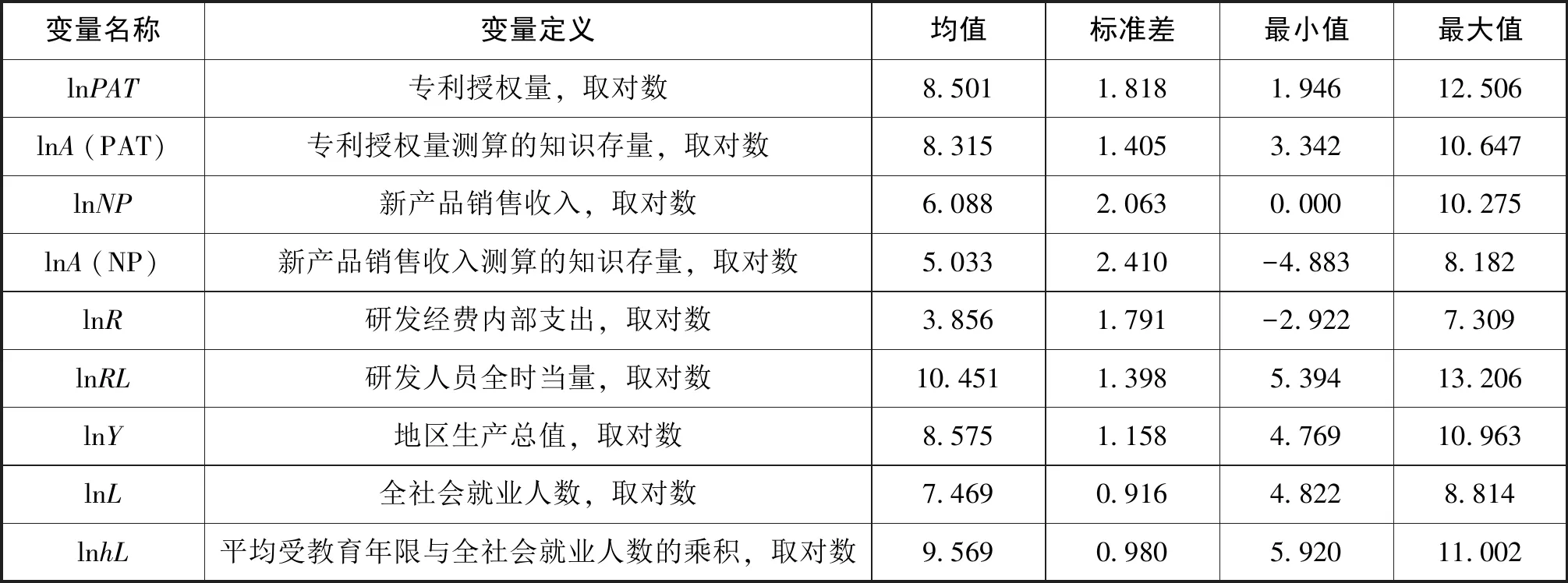
表2 变量定义及描述性统计

2.2 函数形式检验

表3列示了式 (11)的多种估计结果。分别采用专利授权量 (PAT)和新产品销售收入 (NP)衡量新产出知识和测算知识存量，在施加约束β=0时，估计结果如第 (1)和 (2)列所示；在施加约束β=1时，估计结果如第 (3)和 (4)列所示。

当施加约束β=0时，以专利授权量为被解释变量估计的σ=0.130，φ=0.898，均在1%水平上显著异于零，Wald检验拒绝了φ=1；以新产品销售收入为被解释变量估计的σ=0.595，φ=0.425，均在1%水平上显著异于零，Wald检验拒绝了φ=1。

当施加约束β=1时，以专利授权量为被解释变量估计的σ=0.100，φ=0.992，均在1%水平上显著异于零，Wald检验拒绝了φ=1；以新产品销售收入为被解释变量估计的σ=0.302，φ=0.749，均在1%水平上显著异于零，Wald检验拒绝了φ=1。

以上检验结果说明：第一，这期间中国知识生产不存在规模效应，以专利授权量测算的结果同时支持琼斯知识生产函数和熊彼特知识生产函数，前者的对数似然值 (Log-L)更大，说明拟合效果相对更优，以新产品销售收入测算的结果仅支持琼斯知识生产函数；第二，以专利授权量测算的当期研发支出回报率介于0.100～0.130，以新产品销售收入测算的当期研发支出回报率约为0.595，约为前者的5倍。

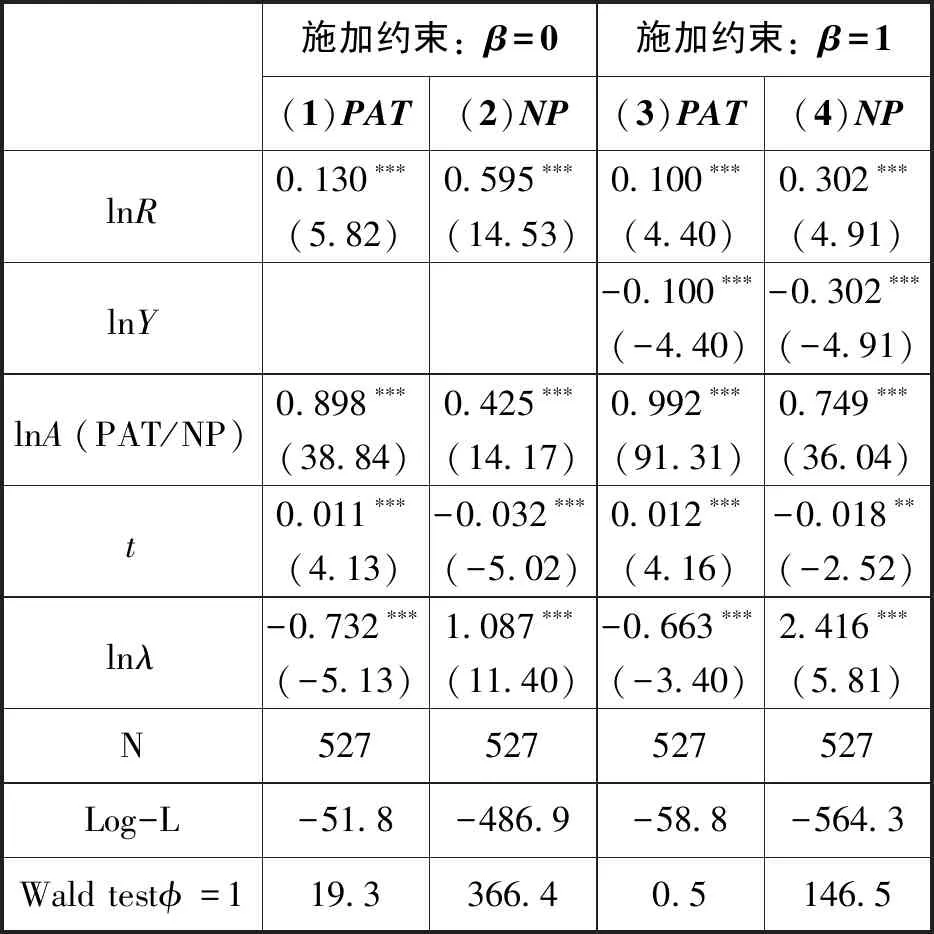
表3 第二代知识生产函数的参数估计结果

注：括号内为T统计量，***、**、*分别表示在1%、5%、10%水平上显著，下同。

2.3 敏感性分析

变量衡量指标的选择是影响估计结果的敏感因素。本文进行两种敏感性检验：第一，用研发人员 (RL)和全社会就业人数 (L)分别代替表3中的研发支出 (R)和地区生产总值 (Y)；第二，考虑到各地人力资本的异质性，将人力资本与全社会就业人数的乘积 (hL)代替全社会就业人数 (L)变量,结果如表4所示。

在施加约束β=0时，将第 (5)和 (6)列与第 (1)和 (2)列对比，除了第 (6)列的时间趋势项不显著外，研发投入和知识存量的显著性均与表3的结果一致，前者的系数略微增大，后者的系数十分相近，Wald检验均拒绝了φ=1。

在施加约束β=1时，将第 (7)和 (8)列与第 (3)和 (4)列对比，研发投入、知识存量及时间趋势项的显著性与表3均一致，第 (8)列与第 (4)列的系数大小非常相近，第 (7)列研发人员的系数比第 (3)列研发支出的系数小了近1/2，知识积累和时间趋势项的系数非常相近。将第 (9)和 (10)列与第 (7)和 (8)列对比，第 (10)列与第 (8)列的结果基本一致，第 (9)列研发人员的系数比第 (7)列研发人员的系数提高了约52.7%，知识存量和时间趋势项的系数基本一致。Wald检验在PAT下均无法拒绝原假设，在NP下均拒绝了φ=1，这与表3的结果一致。

从敏感性分析结果来看，表4所得结论与表3基本一致，这在一定程度上说明了本文所得结论具有可靠性。

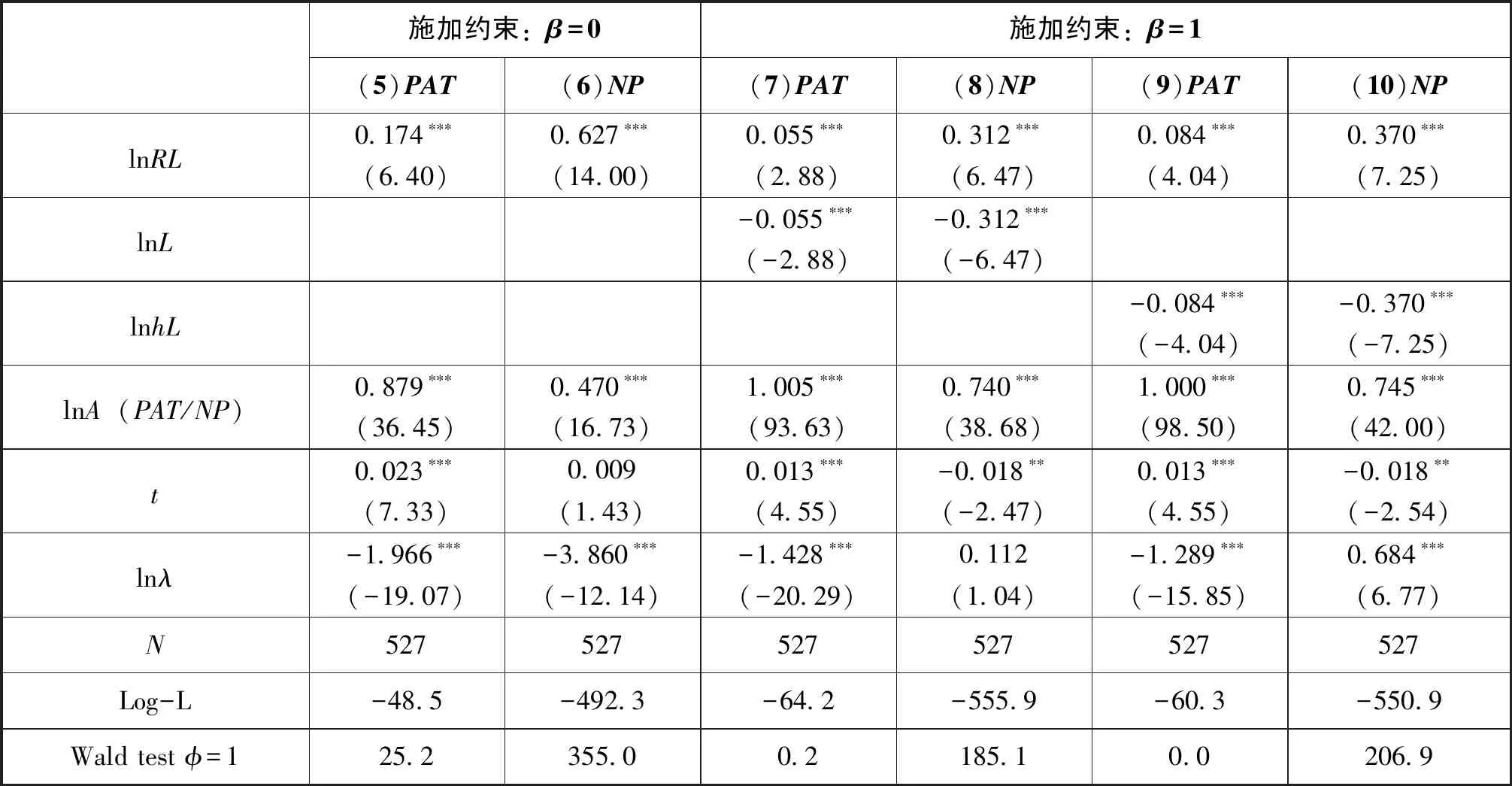
表4 敏感性检验结果

3 循环累积效应的估计结果及分析

利用上述分析，可以得到第二代知识生产函数的各参数值和具体的函数形式。本文利用式 (5)和表3第 (1) (2)列所得参数估计2000—2016年区域研发投入的循环累积效应,并对结果进行分析。

3.1 估计结果

根据式 (5)，当使用专利授权量进行计算时，代入第 (1)列的参数，可以得到：

CCEPAT=lnPATit-0.130×lnRit-0.898×

lnAi0+0.732

(12)

当使用新产品销售收入进行计算时，代入第 (2)列的参数，可以得到：

CCENP=lnNPit-0.595×lnRit-0.425×lnAi0-1.087

(13)

据此，可以估计出历年各区域的研发投入循环累积效应，主要年份的结果如表5所示。从区域均值来看，当使用专利授权量 (PAT)估计时，这期间区域研发投入的循环累积效应 (CCE)平均值约为1.264，江苏、浙江、重庆和西藏居于全国前列，CCE平均值超过了2.0；海南、辽宁、吉林和内蒙古最低，CCE平均值低于0.8；江西、山东、陕西和河南与全国平均水平相近。当使用新产品销售收入 (NP)估计时，这期间区域研发投入的循环累积效应 (CCE)平均值约为0.515，天津、重庆、浙江、海南和吉林居于全国前列，CCE平均值超过1.0；甘肃、黑龙江和陕西最低，CCE均值为负数；湖北、江西、上海、贵州和河南与全国平均水平相近。由此可见，使用PAT估计的CCE结果与使用NP估计的CCE结果存在明显差异。

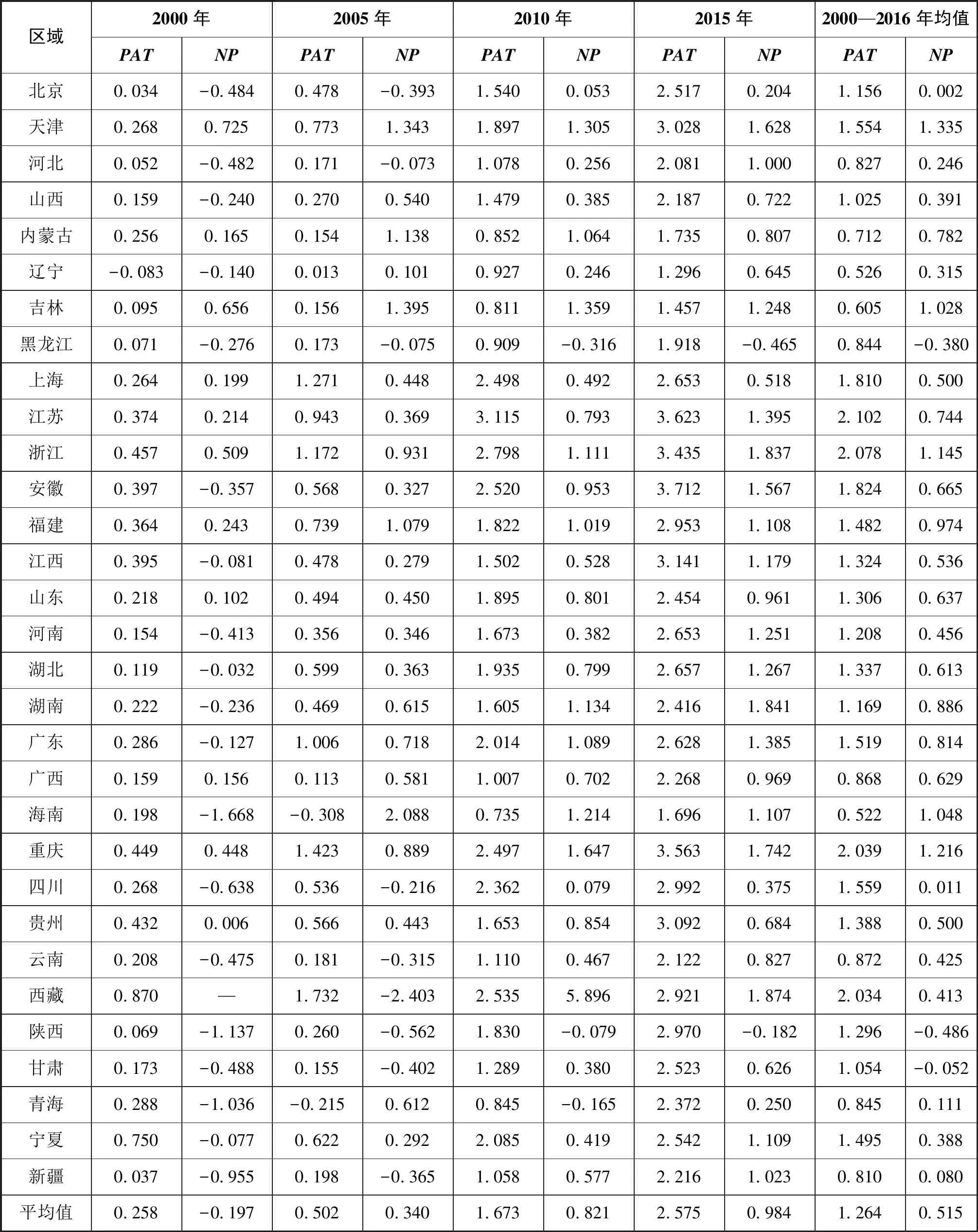
表5 各区域主要年份研发投入循环累积效应的估计结果

3.2 结果分析

从区域研发投入循环累积效应 (CCE)的整体性来看，如图1所示，使用PAT和NP估计的CCE年度均值呈现持续上升的变化趋势，说明这期间研发投入的循环累积效应正在不断增强。东部地区的研发投入循环累积效应相对较强，CCEPAT和CCENP的年度均值在绝大多数年份都高于全国平均水平。西部地区的CCEPAT与全国平均水平相近，中部地区的CCEPAT最低，变化趋势与全国平均线基本一致，说明这期间三大地区间的研发投入和专利产出总体上维持相对平衡的增长态势。中部地区的CCENP与全国水平相近，西部地区的CCENP最低，受到全球金融危机的冲击，2009年和2010年东部地区新产品销售收入大幅下降，导致CCENP低于全国平均水平，2011年以后又恢复到东部>中部>西部的格局。这意味着，同等研发投入投向东部地区比投向中西部地区将获得更高的知识产出。因此，追求效率目标的市场主导型创新模式将倾向于把更多研发资源投向东部地区，从而获得更高的知识产出回报，追求公平目标的政府主导型创新模式则更倾向于将研发资源投向中西部地区，从而缩小其与东部地区的知识产出差距。

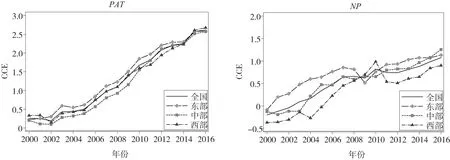
图1 研发投入循环累积效应的年度均值

从区域研发投入循环累积效应 (CCE)的差异性来看，如图2所示，这期间中国CCEPAT在2010年之前持续上升而后趋于平稳，CCENP经历了2000—2006年的上升期、2007—2010年的振荡期和2011年以后的平稳期三个阶段。该结果说明，中国研发投入循环累积效应的区域差异主要形成于2010年以前，现阶段已经逐步趋于稳定。这意味着，初始条件和循环累积效应对知识产出差异的自发调节作用有限，在市场力量作用下落后地区将陷入恶性循环，发达地区将进入良性循环，形成一种 “马太效应”。因此，落后地区改变恶性循环局面的出路只有逐渐提高研发投入和引进高技能人才，并不断改善区域内部和外部的创新环境，以此逐步增强研发投入的循环累积效应。

从区域研发投入循环累积效应 (CCE)的稳定性来看，使用PAT估计的CCE结果比使用NP估计的CCE结果稳定性更高。如图3所示，使用PAT估计的CCE增长率出现负值的斑点主要集中在2005年之前，而使用NP估计的CCE增长率出现负值的斑点明显更多、分布更均匀。该结果说明，这期间中国研发投入与专利产出之间的循环累积因果关系较为稳定，各区域研发投入对专利授权量普遍具有持续提升效应。相反，研发投入与新产品销售收入之间的循环累积因果关系较不稳定，研发投入对新产品销售收入的提升作用未表现出持续性。这意味着，比较而言，研发投入存在更为明显的专利导向，这可能与中国过去形成的 “专利竞赛”制度有关，特别是对地方政府官员的考核过度强化专利产出数量，忽视了知识产出的价值实现能力，造成了所谓的 “创新冗余”问题[18]。因此，为了降低区域研发投入的 “创新冗余”程度，就需要打破 “专利竞赛”制度，将知识产出的价值实现能力作为衡量创新绩效的主要标准。

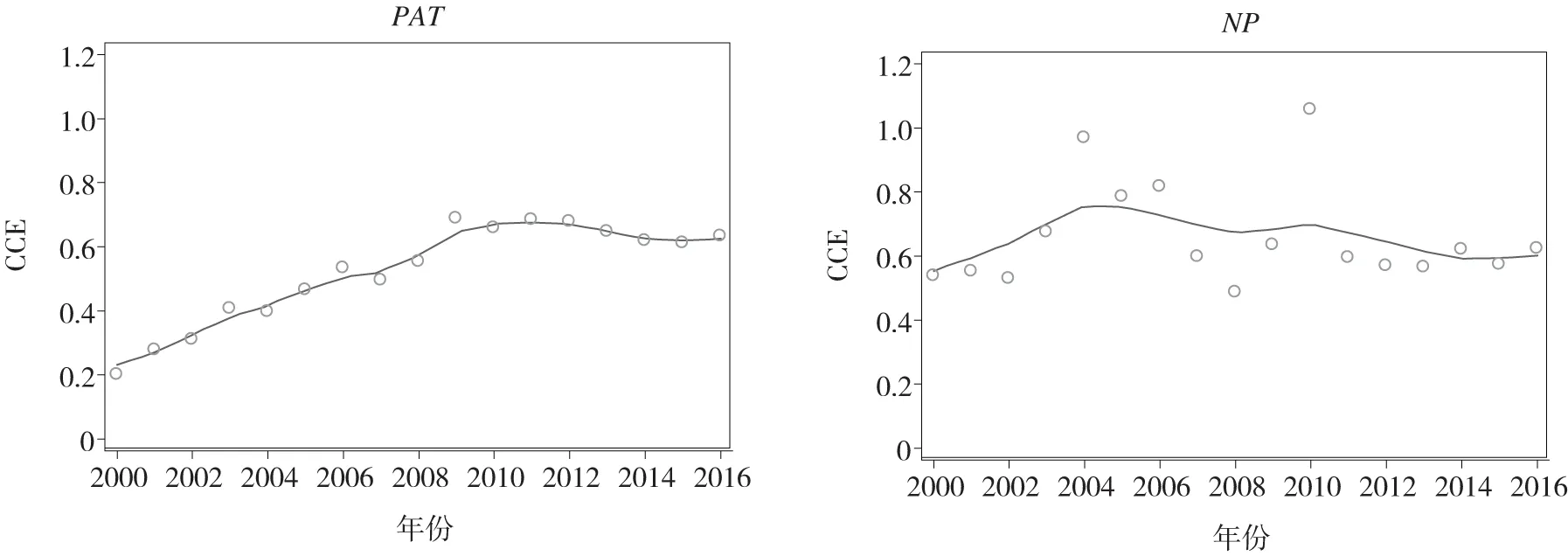
图2 研发投入循环累积效应的年度标准差

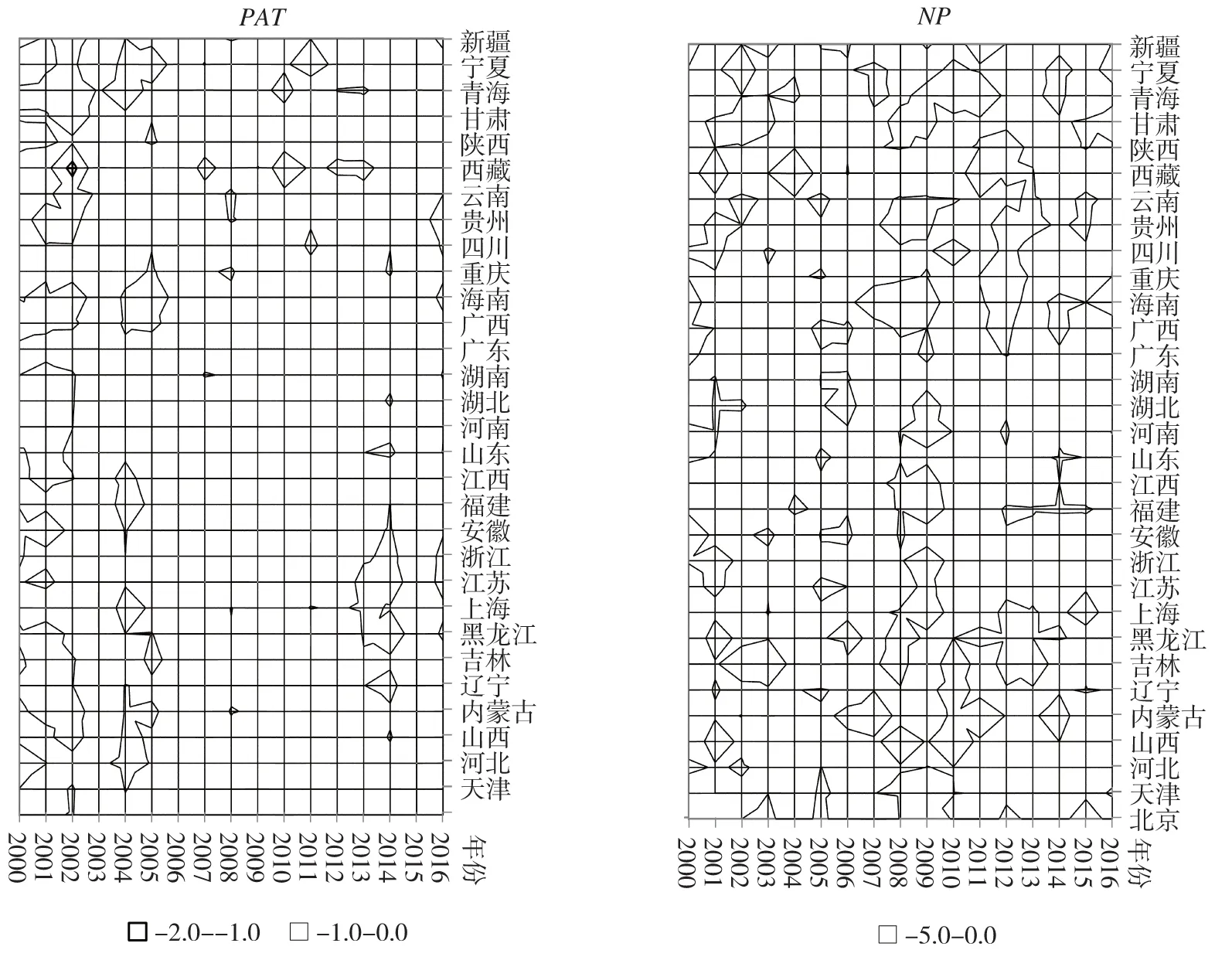
图3 研发投入循环累积效应的增长率斑点图

4 结论与启示

本文以新经济增长理论和循环累积因果关系理论为基础，提供了一个估计研发投入循环累积效应的宏观分析框架，运用该框架首次估计了2000—2016年省级区域研发投入的循环累积效应。研究表明：第一，这期间知识生产不存在规模效应，新产品销售收入数据仅支持琼斯知识生产函数，专利授权量同时支持琼斯知识生产函数和熊彼特知识生产函数，但前者的拟合效果相对更优；第二，知识产出衡量指标的选择对研发投入循环累积效应的估计具有显著影响，使用专利授权量衡量知识产出比使用新产品销售收入衡量知识产出所估计的研发投入循环累积效应更为稳定；第三，这期间研发投入的循环累积效应总体上呈现不断增强趋势，研发投入循环累积效应的区域差异主要形成于2010年以前，现阶段已趋于稳定。

基于上述分析，本文得到如下启示：第一，研发投入的去向应与经济发展目标相一致，追求效率目标应当遵循市场主导型创新模式，将更多研发资源投向循环累积效应更强的东部地区，追求公平目标则应该遵循政府主导型创新模式，将研发资源投向中西部地区，从而逐步提升中西部地区的循环累积效应，缩小其与东部地区的知识产出差距；第二，落后地区要警惕陷入研发创新的恶性循环当中，多措并举逐步提高研发投入强度和减少高技能人才的流失，不断改善区域内外部的创新环境，增强研发投入的循环累积效应；第三，研发投入的终极目标是实现经济的高质量发展，而非 “专利竞赛”，这就要求研发成果要能够满足市场需求，在市场中创造经济价值，因此，衡量创新绩效的主要标准应该从成果的数量向将成果的价值实现能力转变。