湿煤颗粒聚团碰撞解聚的离散元模拟研究
2019-12-24翟酉湘熊晓燕
翟酉湘,熊晓燕,唐 建
(太原理工大学 机械工程学院,山西 太原 030024)
潮湿细粒煤由于带有水分,使颗粒黏附在一起,形成聚团变为难筛颗粒甚至阻碍颗粒,进而在筛分的过程中,堵塞筛孔,恶化筛分环境[1],极大的降低了筛分效率。
焦红光等[2]通过理论计算,认为液桥力是形成聚团影响筛分效率的主要原因。赵跃民等[3]针对潮湿细粒煤筛分透筛机理的研究提出:减小颗粒粘聚提高松散程度,可增大透筛概率提高筛分效率。焦杨[4,5]等使用高速摄像机拍摄了包衣结构湿煤聚团与金属板的碰撞行为,总结了湿煤聚团碰撞解聚的三种分离模式,提出聚团的解聚是碰撞打破了内部颗粒速度的一致性。进而通过离散元方法中的线性接触模型、库仑滑移模型和平行粘结模型模拟了湿煤聚团的碰撞行为,获得了与实验一致的仿真结果[6]。
本文采用BPM(Bonding Particle Model)粘结模型模拟湿颗粒间液桥的粘结行为,在离散元软件EDEM中通过API构建了等径颗粒的湿煤聚团,模拟了湿煤聚团与筛板不同加载条件下的碰撞解聚行为,分析了不同初始速度,旋转速度、筛板倾斜角度下聚团的解聚规律。为驰张筛分机的结构设计与改进提供一定依据。
1 液桥理论
1.1 液桥几何
颗粒聚团中液体的存在形式,与液体的含量有关。根据液体含量的多少,在聚团内液体以钟摆状、环索状、毛细管状、浆液状四种不同的状态存在。对于开采出来原煤,其水分含量多处于7%到14%之间,则此时聚团内的水分以摆动状态存在[7],聚团内的颗粒之间通过液桥粘连在一起。
对于粗糙颗粒之间的液桥,张昭[8]根据两个粗糙颗粒的表面粗糙度,在两个不等径的光滑颗粒之间设定特定的间距,进而可以利用两球形颗粒之间的液桥及其受力情况来表征粗糙颗粒之间的液桥,如图1所示。对于两球形颗粒之间的液桥,用一段圆弧来近似替代液桥与大气的气液界面轮廓,从而得到了液桥几何形貌中的各变量关系与液桥力的简化计算方法。
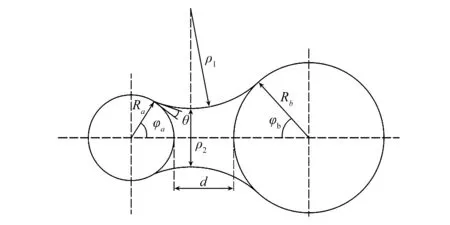
图1 不等径球形颗粒间的液桥
其中,Ra、Rb分别为两颗粒的半径;d为由粗颗粒表面粗糙度得到的颗粒间距,则有填充角φa、φb的关系为:
1.2 静态液桥力
静态的液桥黏附力来源于气液界面上的表面张力和液桥曲面引起的毛细现象,其中表面张力与液桥的表面形态有关,毛细力与液桥曲率有关。从而两颗粒间的静态液桥力取决于液桥的几何形貌。在使用圆弧简化后,可得到以下表达式[9]:
其中:
ρ2=R1sinφa-ρ1[1-sin(φa+θ)]
式中,σ为水的表面张力系数;θ为水煤之间的固液接触角。
1.3 动态液桥力
在两颗粒的分离过程中,由于颗粒间的相对运动而使颗粒间的液桥产生阻力,可以用以下方法计算[10]。
式中,η为液桥液体的粘度;vn为颗粒分离时的相对速度。
1.4 液桥断裂距离
颗粒之间的液桥能否稳定存在,与颗粒间的距离有关。在湿煤聚团碰撞解聚的过程中,聚团内颗粒间发生相对运动,液桥受到拉伸,改变了液桥稳定距离。当颗粒间距达到一定程度,液桥发生断裂。保持液桥稳定的距离亦即液桥发生断裂的距离,称为液桥极限距离。与水煤之间的接触角和液桥的体积有关[11]。
2 离散元模拟
聚团的碰撞解聚行为是一个瞬态的动态过程,而且聚团内的颗粒尺寸处于细观尺度,采用实验的方法难以精确的捕捉到聚团在碰撞过程中的各项物理信息。从而使用离散元方法对碰撞过程进行计算机模拟正在成为研究颗粒体系的有效手段。
2.1 粘结模型
在EDEM软件中,含有液桥的湿颗粒聚团的粘结行为可以使用离散元方法中的Hertz-Mindlin with Bonding接触模型进行表征。该接触模型通过在颗粒之间生成“粘结键”将小颗粒粘结成聚团,这个粘结键可以承受切向力和法向力的作用,当颗粒之间的粘结达到最大法向应力和最大切向应力时,则判定粘结键断裂。如果一个小颗粒周围的所有粘结键全部断裂,那么小颗粒则从聚团中脱离,出现解聚现象。粘结键断裂的判断依据可以通过下列公式计算:
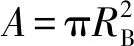
2.2 聚团模型及参数设置
采用EDEM软件构建模型[12]得到由等径小颗粒粘结而成的湿煤聚团模型。采用直径为0.5mm的560个小颗粒生成直径为5mm的球形聚团,小颗粒之间的粘结键数量为2269,如图2所示。

图2 颗粒聚团及其粘结键
为了模拟聚团在筛板上的碰撞,令聚团在重力的作用下,下落0.4m之后与筛板碰撞。为了研究聚团的碰撞解聚信息并简化运算模型,将含有筛孔的筛板简化为一实心的碰撞版进行计算机模拟。模拟中采用的粘结参数通过查阅文献[6,13]获得,见表1。DEM Solutions公司根据数十年的工程经验总结得到材料属性与接触参数的选择方法,生成GEMM数据库,模拟中采用的材料属性和接触参数引自该数据库,见表2、表3。

表1 颗粒粘结参数

表2 模拟实验材料参数

表3 材料接触参数
2.3 碰撞解聚过程
赋予颗粒聚团0.8m/s竖直向下的初速度,在重力的作用下下落0.4m后与筛板碰撞,到达筛板时颗粒聚团的速度为1.192m/s模拟过程中聚团内部颗粒间的粘结和颗粒的速度分布如图3所示。

图3 碰撞解聚过程粘结及速度分布(m/s)
由图3(a)可知,在聚团与筛板接触之前,聚团内部各小颗粒具有一致的速度。在聚团与筛板碰撞接触的瞬间,图3(b)中接触点附近的小颗粒速度减小,与聚团中周围的其余颗粒速度相差较大,在聚团与筛板碰撞接触的区域内,颗粒之间的粘结发生断裂。碰撞区域垂直向上的区域小颗粒速度减小,但速度方向仍然一致垂直向下,聚团周围的小颗粒速度大小以及方向没有发生明显的变化,这两部分区域内,颗粒之间的粘结并未发生断裂。
随着聚团的继续下落,碰撞初始接触区域的部分小颗粒接触筛板后脱离聚团如图3(c),速度方向由原来的竖直向下开始变为向四周扩散,使得碰撞初始接触区域聚团内部颗粒相互碰撞,颗粒之间速度差异较大,颗粒间的粘结键断裂,并由下向上扩展,在聚团内部出现一个空腔。聚团整体的速度减小,聚团内颗粒的速度方向围绕中心碰撞区域向四周分散。
碰撞继续深入,如图3(d)聚团与筛板最先接触的小颗粒与筛板碰撞脱离聚团后,经过筛板反弹速度方向改变为向上,使得粘结破坏区域进一步向上扩展。聚团上部的颗粒速度方向开始出现分化,速度方向由原来的水平向下开始趋于水平方向向四周扩散,聚团内部粘结破坏的空腔区域进一步扩大。
聚团继续下落,碰撞进一步深入,如图3(e)聚团与筛板接触一侧小颗粒之间的粘结基本全部破坏之后,碰撞能量减小,聚团上部部分小颗粒之间的速度分化并不显著,不足以打破颗粒之的粘结,形成次级聚团继续下落,进而发生与筛板的二次碰撞。由于此时次级聚团的速度较小,二次碰撞后往往不能继续解聚。
3 模拟结果分析
为了描述湿煤聚团的解聚程度,使用粘结键的破坏率来定义参数k:
k=破坏的粘结数/生成的粘结总数×100%
由上式可以看出,如果参数为零,则聚团内部液桥没有发生断裂,湿煤聚团保持完整。如果聚团内的液桥发生断裂,则聚团内的粘结键数目减少,而且随着液桥破坏数量的增大,粘结破坏百分比k也随之增大。
3.1 碰撞速度对解聚程度影响
为了研究碰撞速度对聚团解聚程度的影响,分别给与聚团一定的初始速度,在重力的作用下,碰撞时速度分别为0.692m/s,0.892m/s,1.192m/s,1.392m/s,1.892m/s。聚团碰撞速度与解聚程度之间的关系如图4所示。由图4可以看出,粘结的破坏程度随着碰撞速度的增加而增大。在碰撞的初始阶段,粘结的破坏率存在一段短暂的缓慢增长过程,此时对应图3(b);之后由于聚团的速度迅速减小,大部分动能转化为液桥的断裂能量如图3(c)、(d),粘结的破坏率迅速增大,是整个碰撞过程中的主要阶段,大部分粘结在这个阶段中破坏;在迅速破坏阶段之后,粘结破坏率的增速减小,粘结破坏率趋于稳定,整个解聚过程基本完成,而且随着碰撞速度的增大,聚团解聚程度达到稳定所需要的时间减小。与包衣结构聚团[6]相比,等径小颗粒构成聚团的碰撞解聚过程同样经历缓慢破坏、快速破坏、完全破坏三个阶段,但是破坏区域首先发生在中心部位。碰撞速度对碰撞解聚程度的影响与包衣结构聚团类似,但是由于能量主要用于液桥破坏而不是转化为中心煤核的动能,达到完全破坏所需的速度相对较小。
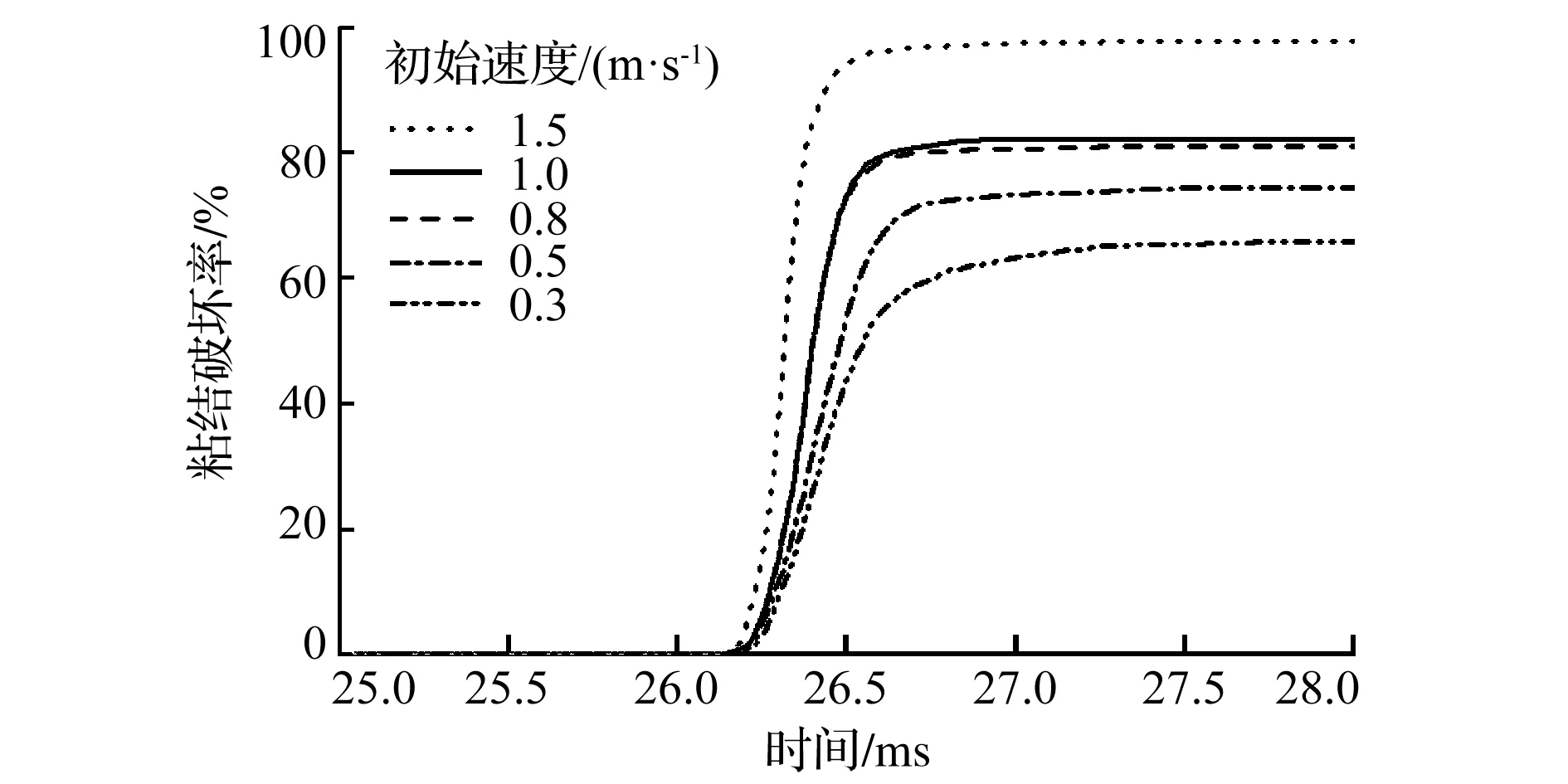
图4 不同速度下聚团解聚程度
3.2 筛板倾斜角度对解聚程度的影响
在筛分过程中筛板存在驰张运动,颗粒聚团与筛板接触时,往往不是正向碰撞。聚团的速度方向与筛板存在一定角度。为了研究筛板倾斜角度对聚团解聚程度的影响,设定筛板与水平方向倾斜角度分别为10°、20°、30°、40°、50°,设定聚团的初始速度为1m/s,在重力的作用下,碰撞时速度为1.392m/s。不同筛板角度下聚团的解聚程度如图5所示。由图5可以看出聚团的碰撞过程,同样经历了破坏率短暂缓慢增长,迅速增加,趋于稳定三个阶段。而且随着筛板倾斜角度的增大,碰撞方向上的速度分量减小,大部分动能没有转化为液桥断裂需要的能量,粘结的破坏率减小。
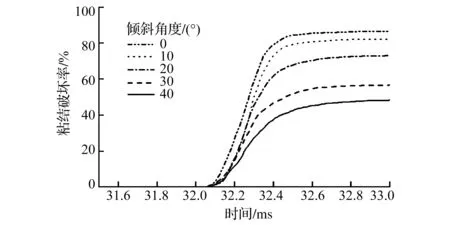
图5 不同筛板角度下聚团解聚程度
3.3 聚团旋转速度对解聚程度的影响
聚团在0rad/s、10rad/s、30rad/s、50rad/s、100rad/s五种不同旋转速度下的解聚程度如图6所示。设定聚团的初始速度为1m/s,在重力的作用下,碰撞时线速度为1.392m/s。可以看出随着聚团旋转速度的增加,聚团中粘结的破坏率增大,但是当颗粒聚团的旋转速度为50rad/s,继续增大聚团的旋转速度到100rad/s,粘结破坏率并没有获得显著的提高。旋转速度对解聚程度的影响与包衣结构聚团[6]类似,增大旋转速度有利于聚团的解聚,但并不是影响粘结破坏率的首要因素。
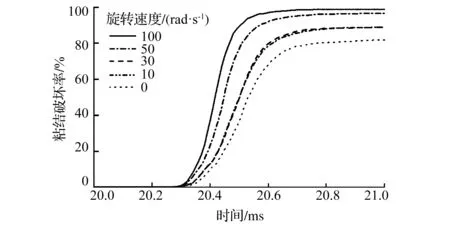
图6 不同旋转速度下聚团解聚程度
4 结 论
1)粘结的破坏区域首先发生在聚团与筛面的接触区,随后由下而上,由中心向四周扩散。在碰撞速度较小的情况下,由于聚团顶部小颗粒距离碰撞区较远,往往不能充分解聚,而形成二级聚团。
2)碰撞后聚团的解聚程度随着碰撞速度的增大而增大,随着筛板倾斜角度的增大而减小。增大聚团的旋转速度有助于聚团的碰撞解聚。
3)与包衣结构聚团相比,等径小颗粒构成聚团的碰撞解聚过程同样经历缓慢破坏、快速破坏、完全破坏三个阶段。碰撞速度、旋转速度对等径颗粒聚团碰撞解聚程度的影响与包衣结构聚团类似,但是达到完全破坏所需的速度相对较小。
4)本文仅就单一因素的影响进行了模拟研究,不同速度、不同筛板角度与不同旋转速度之间的交互作用对聚团粘结破碎的影响规律还有待进一步研究。
