基于顺序统计量的索引调制信号检测方法
2019-12-24陆发平刘传辉康家方
陆发平 ,刘传辉 ,康家方
(1.海军航空大学,山东 烟台 264001; 2.山东省信号与信息处理重点实验室,山东 烟台 264001)
0 引言
随着移动通信、虚拟现实、大数据和物联网的不断发展,不同信息载体间信息交互水平的不断提高,对信息传输速率需求不断提高。在波形设计层面,提高系统信息传输效率的关键在于提高单位时宽、带宽内调制符号的多样性。围绕如何提升调制符号的多样性,相关领域专家学者进行了诸多有意义的尝试,并取得了一系列研究成果,如超Nyquist传输[1-2]、非正交调制[3]、时域波形复用技术[4]等,系统频带利用率不断提升。但由于上述调制技术通过提高单位时间带宽积内用于信息传输的载波信号路数,实现调制符号多样性的提升,调制信号峰均功率比较高,对功放等非线性器件提出更高的要求。那么如何利用尽可能少的载波信号传输尽可能多的信息?载波层面的索引调制给出了一种可行的解决方案,2013年Basar E[6]提出(Index Modulated Orthogonal Frequency Division Multiplexing,OFDM-IM),首次将索引调制应用于OFDM,利用载波索引激活载波符号调制同时进行信息传输,在不增加载波信号的前提下,有效提升了系统频带利用率。自提出之后,得到相关领域专家学者的广泛关注,被应用于5G[7-8]、V2V[9]、V2X[10]、UWA[11-12]、信道分割多址系统[13]及设备识别[14]等领域。虽然OFDM-IM存在诸多优势,被应用诸多领域,但仍旧存在检测算法复杂度高,不易于工程应用的不足。该问题一直是人们持续关注的焦点问题之一,OFDM-IM的提出者E.Basar在OFDM-IM提出之初,便给出了性能次优、复杂度相对较低的LLR检测[6],有效解决了频率选择性信道条件下,ML检测算法复杂度高的不足。J.Crawford等人[15-16]引入贪婪算法,提出基于度贪婪算法的OFDM-IM调制信号检测方法,该方法逐次完成对最高能量峰值的检测,当激活载波数目较多时,算法复杂度也会随之增加。A.I.Siddiq[17]提出一种基于编码的检测算法,该方法能够有效降低检测算法复杂度,但需要在发射端对传输信息进行编码,随着索引对应的信息量增加,系统整体实现复杂度不断增加。因此,如何在不增加系统实现复杂度的前提下,降低OFDM-IM调制信号检测算法复杂度成为目前急需解决的关键问题之一。
在此背景下,结合索引调制符号概率密度分布特点,对不同频率信道衰落参数相同信道条件下,低复杂度OFDM-IM调制信号检测方法展开研究,引入顺序统计量,提出了一种基于顺序统计量的IM调制信号检测方法(Index Modulation Signal Detection Method Based on Order Statistic,OFDM-IM-OS),与ML检测相比,以适当牺牲系统误码性能为代价,有效降低了索引调制信号检测算法复杂度。
1 索引调制基本原理
索引调制是在空间调制基础上发展起来的新型调制技术,区别于空间调制在天线选择上加载信息,载波索引调制在载波选择上加载信息,更加灵活方便,其原理如图1所示。

图1 OFDM-IM调制基本原理
假设OFDM子载波数目为Q=gN,待传输数据共m=gpbit,OFDM-IM的主要步骤如下:
① 将Q个子载波平均划分为g组,每组有N个子载波,每组传输pbit信息。
② 将待传输数据m=gpbit分为g组,每组含有pbit信息。
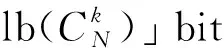
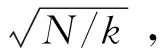
目前,IM调制信号主要检测方法有ML和LLR2种检测方法,ML检测需要对所有载波选择方案进行遍历,然后选择与接收信号间均方误差最小的载波选择方案作为检测输出,但随着载波路数的增加,ML检测算法复杂度呈指数增加,不利于工程实现。为降低索引调制信号检测复杂度,Ertugrual等学者[6]提出了基于LLR的低复杂度检测方法,该方法首先计算载波激活与不激活的后验概率比值,即:
(1)
式中,n为载波总数,k为激活载波个数,yF(α)为第α支路接收信号,N0,F为噪声频域功率,hF(α)为第α支路对应的信道衰落系数,sχ为调制符号。对第α支路而言,λ(α)越大,则第α支路被激活的概率也就越大。然后,对不同支路对应的λ(α)进行比较,将λ(α)绝对值较大的前k个支路判决为激活的载波,并对该k个支路信号进行解调。
比较ML检测与LLR检测可知,LLR检测能够有效降低索引调制信号检测算法复杂度,且在频率选择性衰落信道中,由于不同频率信道衰落参数hF(α)不同,在接收端,不同支路信号检测量不同,采用式(1)的方式能够有效保证系统误码性能。但在高斯白噪声信道条件下,不同频率信道衰落参数hF(α)相同,基于LLR的索引调制检测方法是否能够进一步优化?围绕该疑问,结合高斯白噪声信道条件下OFDM-IM调制信号特点,对低复杂度信号检测方法展开研究。
2 OFDM-IM-OS检测方法基本原理
由统计检测量的概率分布可知,载波激活与未激活时,AWGN信道条件下,接收端载波信号统计检测量的概率分布函数(Probability Distribution Function,PDF)如图2所示。从图2可知,与未被激活的载波信号相比,被激活的载波信号对应的统计检测量出现大幅值的概率较大,这意味着在接收端,对不同支路载波信号对应的统计检测量按幅值绝对值大小进行排序,被激活的载波信号对应的统计检测量排在前面的概率较大。因此,在AWGN信道条件下,可以依据不同支路载波信号对应的统计检测量数值大小,直接判断该载波是否被激活,而无需计算不同载波的LLR,在此思路下,对低复杂度IM调制信号检测方法展开研究。
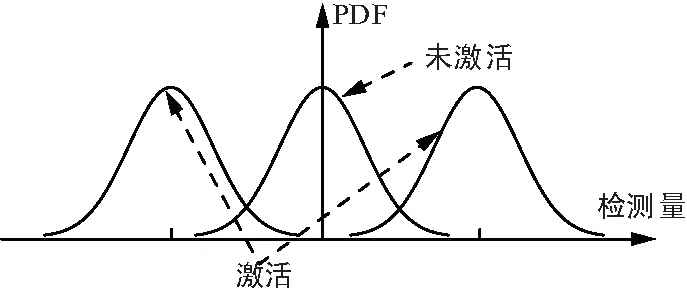
图2 调制符号统计检测量PDF
基于AWGN信道条件下激活与未激活时,统计检测量[18]的差异,引入顺序统计量,提出了一种基于顺序统计量的IM调制信号检测方法,实现以较低算法复杂度对k值固定时,ODFM-IM调制信号的有效检测。对于k值固定时,OFDM-IM-OS检测方法原理框图如图3所示。
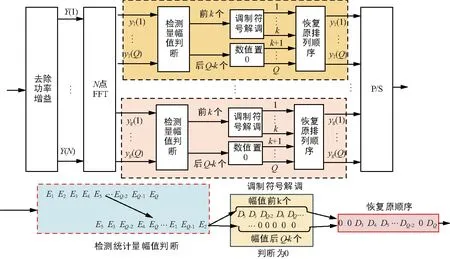
图3 OFDM-IM-OS检测原理框图
检测方法原理的主要步骤如下:
① 对不同支路统计检测量进行幅值(绝对值)比较,按由大到小顺序进行排序;
② 根据脉冲选择方案,对前k个大幅值分量进行判决,后Q-k个统计检测量置0;
③ 对判决结果按支路顺序进行排序,并进行串并转换,恢复发射端发射信号。
3 仿真分析
借助仿真工具,从检测方法算法复杂度和系统误码性能2个方面,对OFDM-IM-OS系统性能进行仿真分析,验证所提信号检测方法的可行性和有效性。
3.1 仿真条件
OFDM调制的码元周期Ts=1 s,载波中心频率为3~18 Hz,取16个交叠为50%的子载波;信道为加性高斯白噪声信道;信息映射模块采用PAM调制;载波选择模块激活载波数分别为(4,2),(8,4),(16,8)。
3.2 仿真结果与分析
3.2.1 检测方法算法复杂度分析
假设并行载波路数为N,调制进制数为M,对不同检测方法的算法复杂度进行分析,旨在说明所提检测方法能够降低检测算法复杂度。
① IM-ML检测方法
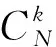
(2)
② IM-LLR检测方法
首先,利用对数似然比判断激活的载波,每个载波的运算量为7M-1;其次,对判断激活的载波支路进行判决,算法复杂度为Mk。故算法复杂度为:
QIM_LLR= (7M-1)N+Mk+Nlb(N)=
13N+k+Nlb(N)。
(3)
由式(3)可知,IM-LLR检测方法的算法复杂度为ϑ(Nlb(N)),当采用二进制时,其算法复杂度仍未为ϑ(Nlb(N))。
③ IM-OS检测方法
IM-OS调制信号检测方法根据检测统计量大小,对不同支路信号的检测量进行排序,对N载波进行排序算法(采用稳定算法归并排序[19])复杂度为Nlb(N),对选择k路进行判决,算法复杂度为Mk,相应的算法复杂度为:
(4)
由式(4)可知,IM-OS检测方法的算法复杂度为ϑ(Nlb(N)),当采用二进制时,其算法复杂度仍为ϑ(Nlb(N))。
随PSWF信号路数增加,不同检测方法运算量变化趋势如表1所示,从仿真结果可知, OFDM-IM-OS检测方法能够有效降低IM调制信号检测算法复杂度,且随着载波数目的增加,相对于IM-ML检测,降低程度不断提高;相对于IM-LLR检测,降低程度不断降低。如当载波数目为4时,相对于IM-ML检测、IM-LLR检测,IM-OS检测算法运算量分别降低50%与81%;当载波数目为8时,相对于IM-ML检测、IM-LLR检测,IM-OS检测算法运算量分别降低97%与76.5%,这表明所提GIM-OS检测方法能够大幅降低索引调制信号检测算法复杂度,与理论分析一致。

表1 不同检测方法运算量
3.2.2 检测方法系统误码性能分析
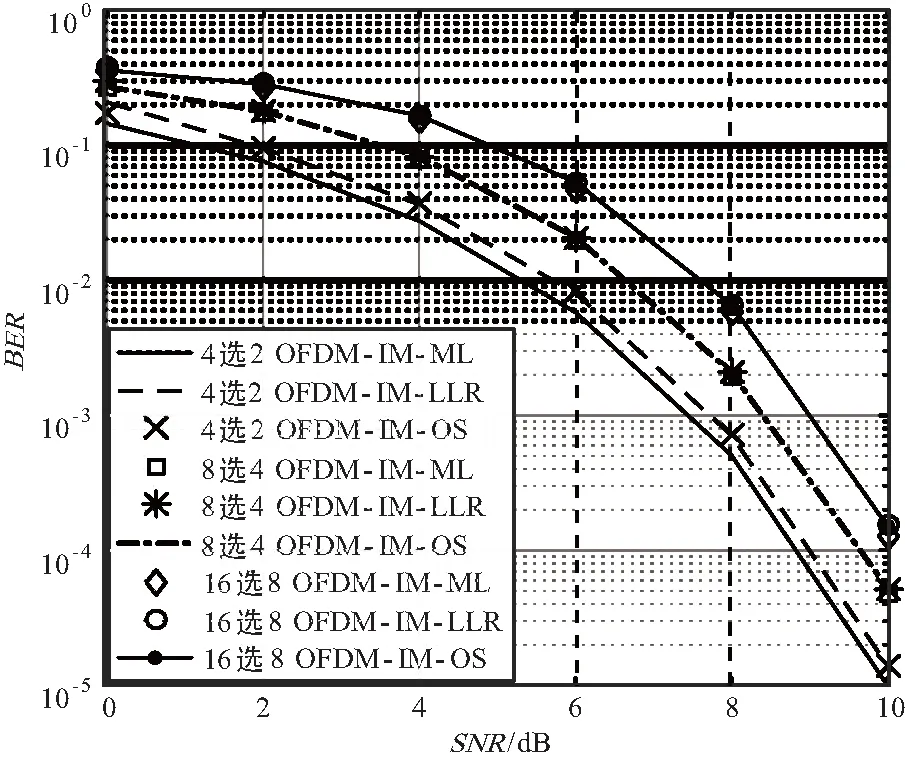
图4 OFDM-IM系统误码特性曲线
4 结束语
围绕如何降低索引调制信号检测算法复杂度,引入顺序统计量,对低复杂度索引调制信号检测方法展开研究,给出了一种基于顺序统计量的OFDM-IM调制信号检测方法。理论与仿真分析表明,该方法在不降低系统误码性能的前提下,有效降低索引调制信号检测算法复杂度。但通过仿真发现,OFDM-IM调制系统误码性能较低,无法满足高可靠性要求的应用场景,因此,如何提高系统误码性能,是下一步索引调制的研究重点之一,也是后续工作的关注重点。
