色散和杂质对双参量非对称高斯势量子点量子比特的影响*

乌云其木格 韩超 额尔敦朝鲁

1) (内蒙古民族大学物理与电子信息学院, 通辽 028043)

2) (河北科技师范学院凝聚态物理研究所, 秦皇岛 066004)

选取双参量非对称高斯势描写量子点中电子的受限效应, 采用LLP-Pekar变换变分法研究了色散和杂质对量子点量子比特性质的影响.结果表明, 量子点量子比特中电子的概率密度随非对称高斯势阱宽的减小而呈现显著振荡, 并随介电常数比的增加而减小; 量子比特振动周期随高斯势阱深的增加或介电常数比的增加而减小; 退相干时间随介电常数比的增加或色散系数的增加而增大; 相位旋转品质因子随介电常数比的增加或色散系数的增加而增大.

1 引 言

量子计算的基本原理是利用量子化的二能级系统作为信息处理的基本单元量子比特, 通过对量子态的调控, 完成复杂计算和信息处理.量子点量子计算机是目前被认为最有希望实现的量子计算机方案之一[1-4], 量子点中的二能级体系可作为一个量子比特.影响量子点量子比特的存储、存活、退相干、旋转操控等性质的要素中, 除了位于量子点中电子的三维受限和电声耦合之外, 还应包括量子点自身的品质, 如介电常数比、杂质、色散等.这些要素都极具研究价值, 且目前亟待理清.对于量子点中电子的三维受限和电声耦合, 选取合适的受限势函数极为重要.长期以来, 用单参量的抛物势来描述量子点中电子的受限情况较为普遍[5-9].然而, 抛物势是一种过于简化了的理想模型, 其结果无疑是比较粗糙的.最近, 一些学者采用高斯势函数描写电子在低维量子结构中的受限, 这是因为一些实验结果[10,11]显示电子真实的受限应是非抛物形的阱状势, 而高斯势阱平滑且具有有限的阱深阱宽, 应是一个很好的近似.然而, 不难发现, 近几年引入高斯限定势研究量子计算机的工作大多集中在量子阱量子比特上[12-15], 而相关研究在最具实际价值的量子点量子比特领域甚少, 尤其是研究色散、杂质和电声耦合对双参量非对称高斯势量子点量子比特的影响的工作尚未报道.本文选取双参量非对称高斯势描写量子点中电子的受限效应, 采用LLP-Pekar变换变分法研究了色散和杂质对量子点量子比特性质的影响.

2 模型与方法

考察一个位于量子点中三维受限的电子, 设电子在沿量子点生长方向及其垂直方向分别受到不同局域限定势作用, 并与介质中氢化杂质和体纵光学(LO)声子相互作用, 则量子点中杂质-电子-LO声子耦合体系的哈密顿量可以写成[12]：

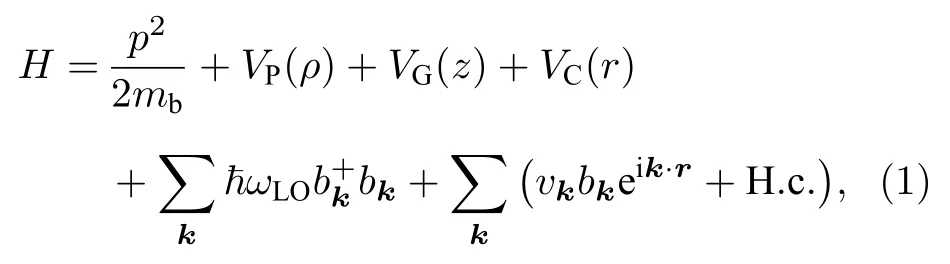
式中

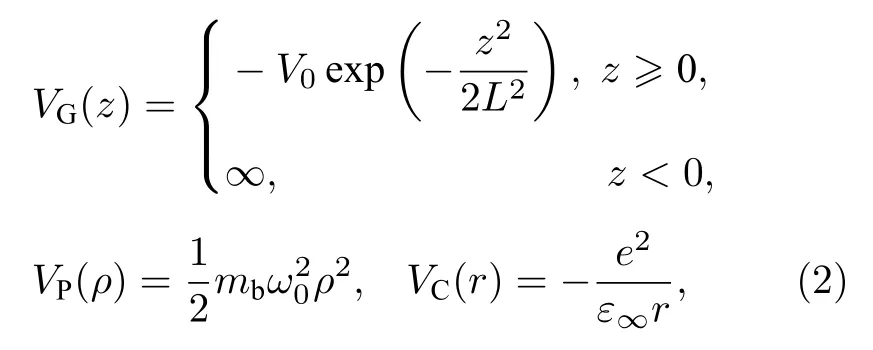
分别表示电子沿量子点生长方向(z轴)及其垂直方向(xy平面)的限定势和电子在氢化杂质电场中的库仑能, 其中,V0表示非对称高斯势的阱深且V0＞0,L表示其阱宽, 亦称为量子点的有效厚度.其余各项各量的物理意义与文献[12]相同.

讨论变分函数U-1HU在态中期待值的变分极值问题, 按照变分原理

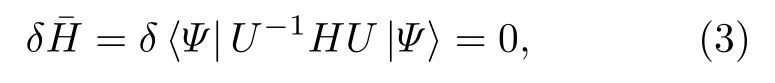
这里算符U是LLP幺正变换[16].依据Pekar类型的变分法[17], 体系的基态和第一激发态试探波函数分别选为

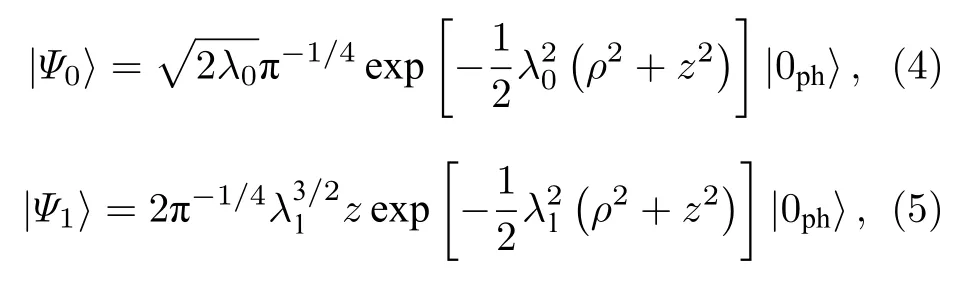
其中,λ0和λ1为变分参数,是 LO 声子的真空态, 由确定.

将(4)和(5)式分别代入(3)式中, 可导出变分参数λ0和λ1满足的方程如下：

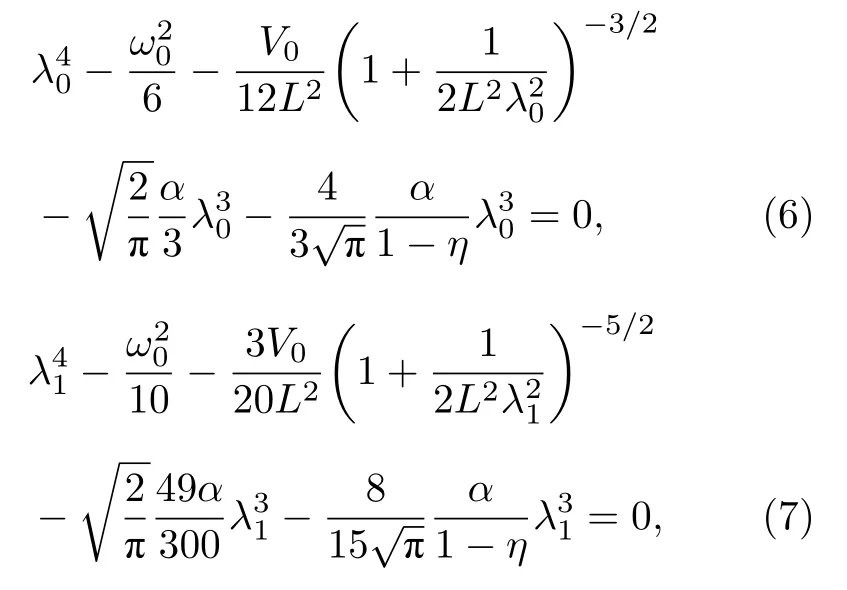
其中η=ε∞/ε0称为介电常数比.利用λ0和λ1并经冗长计算, 可分别得体系的基态和第一激发态能量藉此与(4)和(5)式可以构造一个二能级体系, 当电子处于叠加态

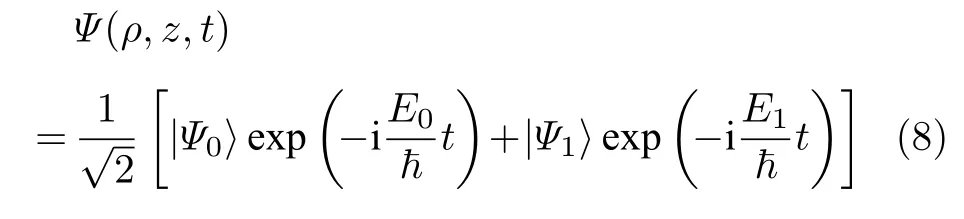
时, 即构成一个量子点量子比特, 量子比特内电子的概率密度为

考虑到电子的叠加态是不稳定的, 极易受到外界环境的影响, 为此, 我们引进抛物色散关系, 基于费米黄金规则和偶级近似, 在环境保持低温的情况下, 引入声子色散关系[5,7,18-20]ω=ωLO-ςck2, 可算得声子的自发辐射率为

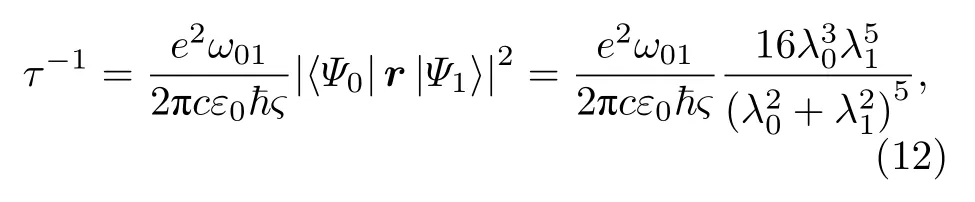
其中,τ为退相干时间,ς称为色散系数.借助(12)式可以展开对量子比特球的相位旋转(或称自由旋转)操控的讨论.对于一个退相干时间为τ的二能级系统, 其量子比特球的相位旋转品质因子Q为

3 结果与讨论

图1—图10给出了非对称高斯势量子点量子比特中电子的概率密度w、振动周期T、退相干时间τ和自由旋转品质因子Q的数据曲线, 为了使这些数值曲线呈现的各物理量的变化规律具有普遍性 , 图中分别以作为时间、能量和长度的单位.

图1表示能隙 ∆E在高斯势不同阱深V0下随其阱宽L的变化.由图1可以看出, 各 ∆E-L曲线呈现两头低、中间高(最大值出现在L≈0.3rp处)、左右非对称的显著特点, 属于一种非对称“高斯分布”, 这与本文采用非对称高斯势VG(z) 描写电子受限有关.由图1 还可以看出, 在给定L下, ∆E随V0的增加而增大, 这是因为 |VG(z)| 随V0增加而增大所致.

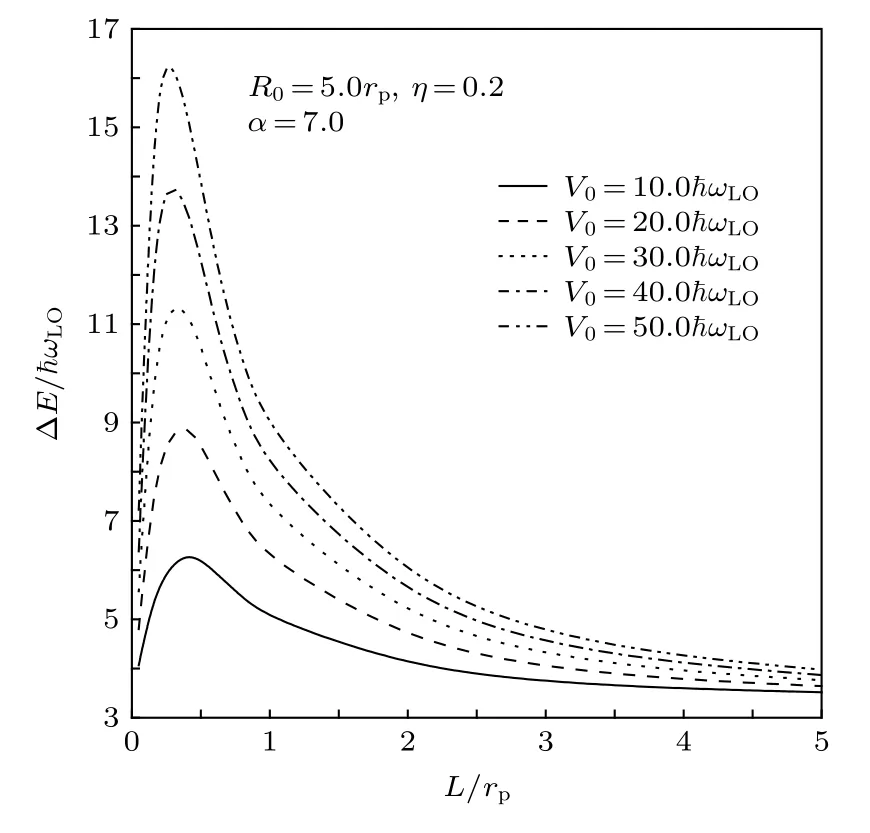
图1 能隙 Δ E 在非对称高斯势不同阱深 V0 下随阱宽L的变化Fig.1.Energy gap Δ E versus the well width L under different the well depth V0 of the asymmetric Gaussian (AG)potential.

图2描绘了能隙 ∆E在不同介电常数比η下随高斯势阱宽L的变化.由图2可以看出, ∆E随η的增加而增大.这是因为在含氢化杂质的晶体或纳米结构中电子被库仑势(VC＜0)束缚于氢化杂质中, 且η越大, 杂质-电子库仑势VC∝-(1-η)-1越强.

图3为概率密度w在高斯势不同阱深V0下随其阱宽L的变化.由图3可以看出,w随L的变化规律在L的不同区域差异较大：当L＞2.0rp时,w随L的增加而增大.这是因为随着L的增加, 电子的纵向受限减弱, 使得体系的能量E随高斯阱宽L的增加而减小, 而根据能量最低原理, 电子优先处于较低的能态; 在L取一定时,w随阱深V0的增加而减小, 这是因为随着V0的增加, 电子的自陷加大, 致使体系的能量E随V0的增加而增大所致.当L＜2.0rp时,w随L的减小而明显振荡变化, 这一结果与量子力学理论相吻合, 因为电子受限越强, 电子态的波动性越凸显.

图4描绘了概率密度w在不同介电常数比η下随高斯势不同阱宽L的变化.由图4可以看出,在L一定时,w随η的增加而减小, 这是因为库仑能 2α/(1-η) 随η的增加而增大, 进而推高体系的能量, 促使电子优先处于较低的能态.

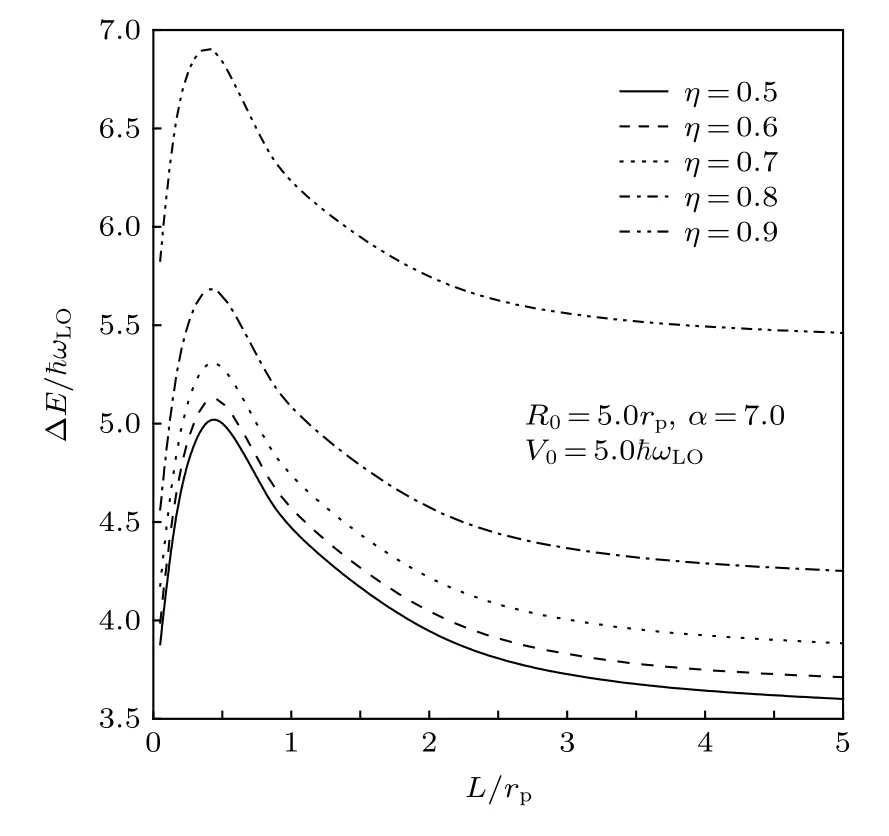
图2 能隙 Δ E 在不同介电常数比 η 下随高斯势阱宽 L 的变化Fig.2.Energy gap Δ E versus the well width L of the AG potential under different the dielectric constant (DC) ratio η .

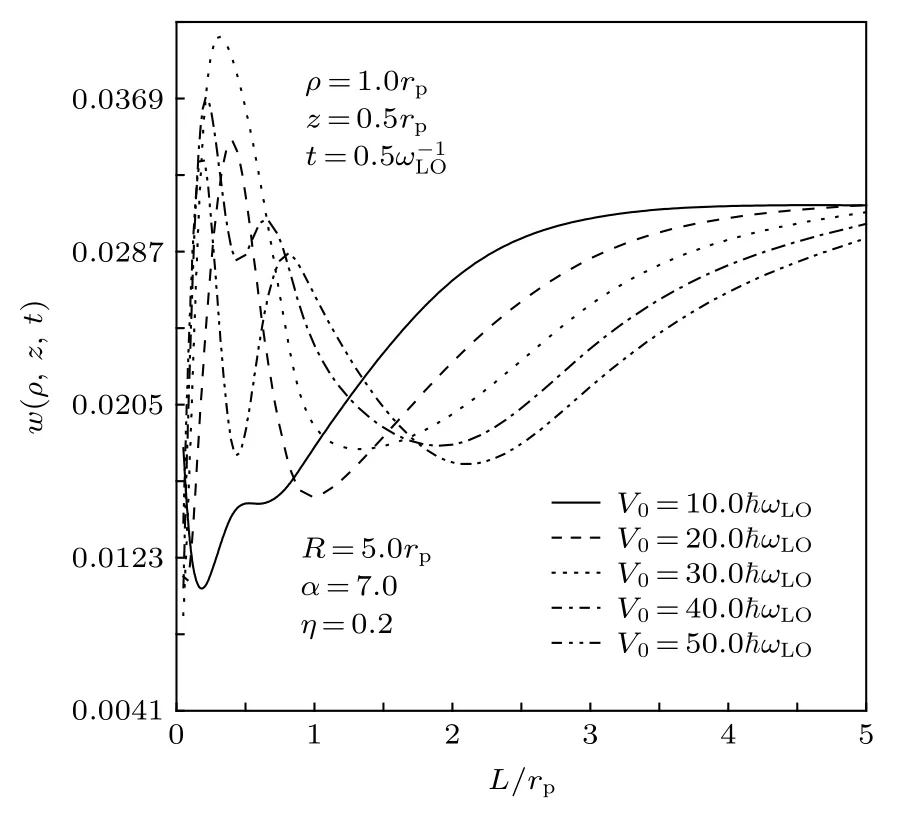
图3 概率密度w在高斯势不同阱深 V0 下随阱宽L的变化Fig.3.Probability density w versus the well width L under different the well depth V0 of the AG potential.

图5揭示了振动周期T在高斯势不同阱深V0下随其阱宽L的变化.由图5可以看出,T-L曲线呈现两头高、中间低(最小值出现在L≈0.3rp处)、左右非对称的显著特点.这与图1恰好相反, 这是由于T∝1/∆E.这一最小值对于量子比特信息存储是不利的, 因此选择量子点的厚度应远大于L≈0.3rp.在L一定时,T随阱深V0的增加而减小, 这是因为 ∆E随着V0的增加而增大.这意味着深阱量子点也不利于量子比特信息的存储.

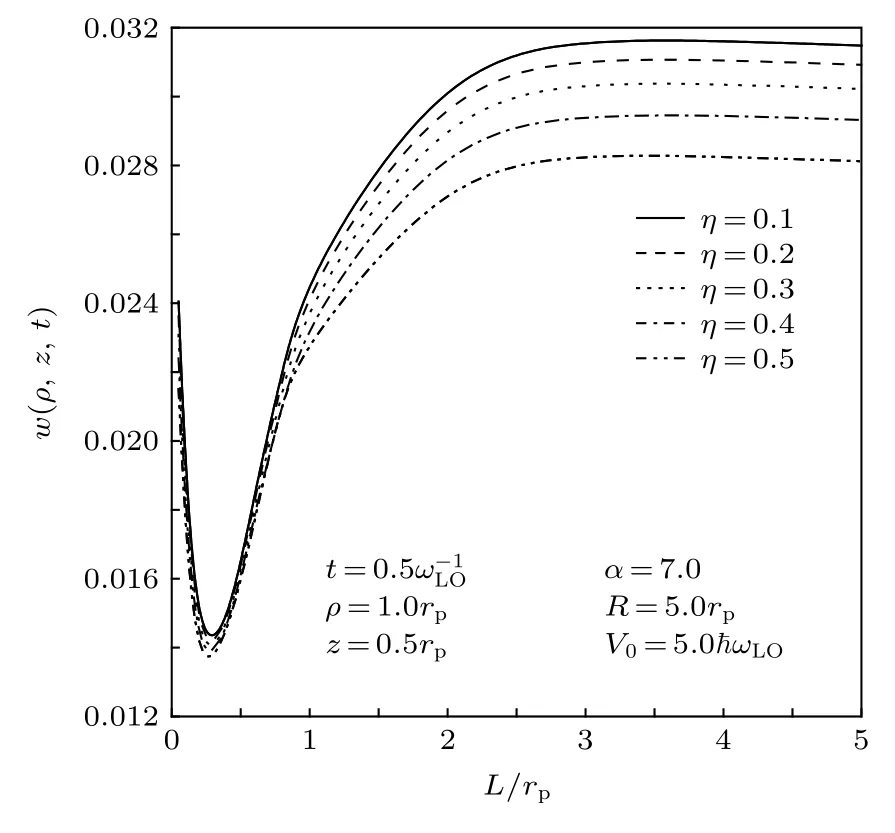
图4 概率密度 w 在不同介电常数比 η 下随高斯势不同阱宽L的变化Fig.4.Probability density w as a function of the well width L of the AG potential at different the DC ratio η .

图5 振动周期 T 在高斯势不同阱深 V0 下随其阱宽 L 的变化Fig.5.Variations of oscillation period T as a function of the well width L at different well width L of the AG potential.

图6 描写了振动周期T在不同介电常数比η下随高斯势阱宽L的变化.由图6可以看出, 当L一定时,T随η的增加而减小, 这是因为 ∆E随η的增加而增大.这表明量子点中杂质的存在, 使得电子叠加态的振荡周期变小, 而振荡周期的变小,意味着量子位存活时间变小.这对于量子点量子比特的信息存储是不利的.

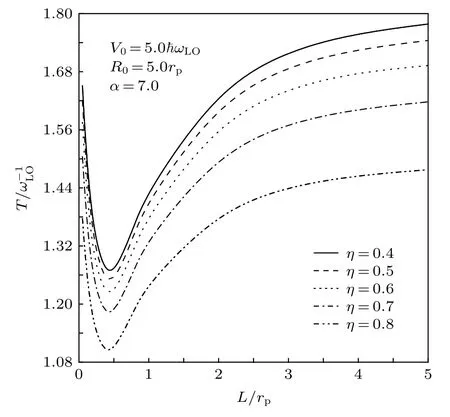
图6 振动周期 T 在不同介电常数比 η 下随高斯势阱宽L的变化Fig.6.Variations of oscillation period T as a function of the well width L of the AG potential at different the DC ratio η .

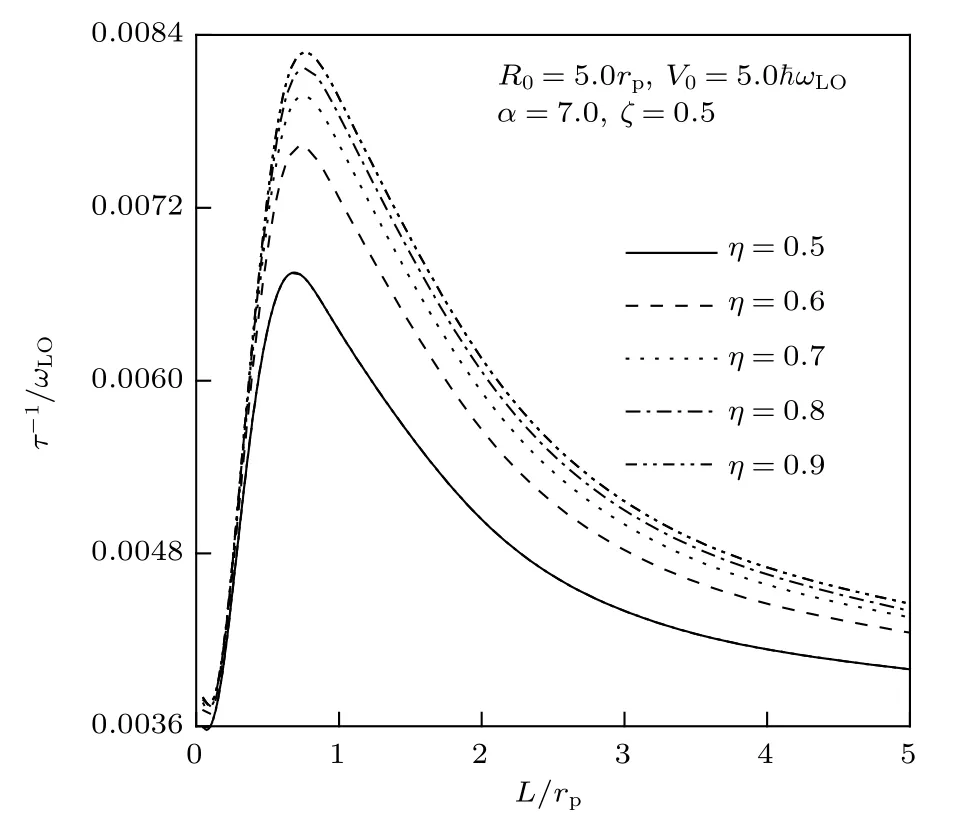
图7 自发辐射率 τ -1 在不同介电常数比 η 下随高斯势阱宽L的变化Fig.7.Spontaneous emission rate τ -1 as a function of the well width L of the AG potential at different the DC ratio η .

图7描绘了声子自发辐射率τ-1在不同介电常数比η下随高斯势不同阱宽L的变化.由图7可以看出,τ-1-L曲线呈现两头低、中间高、左右非对称形状.由(12)式不难看出这是由于 ∆E-L曲线的非对称高斯分布传导至τ-1-L曲线所致.自发辐射率τ-1的最大值出现在L≈0.7rp处, 换言之, 在L≈0.7rp处退相干时间τ取最小值, 这对量子比特的信息存储是最不利的.由图7还可以看出,τ-1随η的增加而减小, 这意味着退相干时间τ随η的增加而增大.这表明量子点中杂质库仑势的存在对于量子点量子比特的信息存储是有利的.

图8表示了自发辐射率τ-1在不同色散系数ς下随高斯势阱宽L的变化.由图8可以看出,τ-1随ς的增加而减小, 这意味着退相干时间τ随ς的增加而增大.色散系数是由材料本身性质决定, 因此要想获得较长的退相干时间应选择色散系数较大的材料来制备量子点量子比特.

图9表示相位品质因子Q在不同介电常数比η下高斯势不同阱宽L的变化.由图9可以看出,Q-L曲线呈现“γ”形特点, 最小值出现在L≈0.8rp处.由(12)和(13)式不难看出, 该曲线是一个被∆E调节的τ-L曲线.由图9 还可以看出,Q随η的增加而增大, 这表明杂质库仑势的存在有利于相位旋转操控.图10描绘了相位品质因子Q在不同色散系数ς下随高斯势不同阱宽L的变化.由图10可以看出,Q随ς的增加而增大, 这意味着选择色散系数越大的材料制备量子点, 其量子比特球越容易实施相位旋转操控.

图8 自发辐射率 τ -1 在不同色散系数 ς 下随高斯势阱宽L的变化Fig.8.Spontaneous emission rate τ -1 as a function of the well width L of the AG potential at different dispersion coefficient ς .

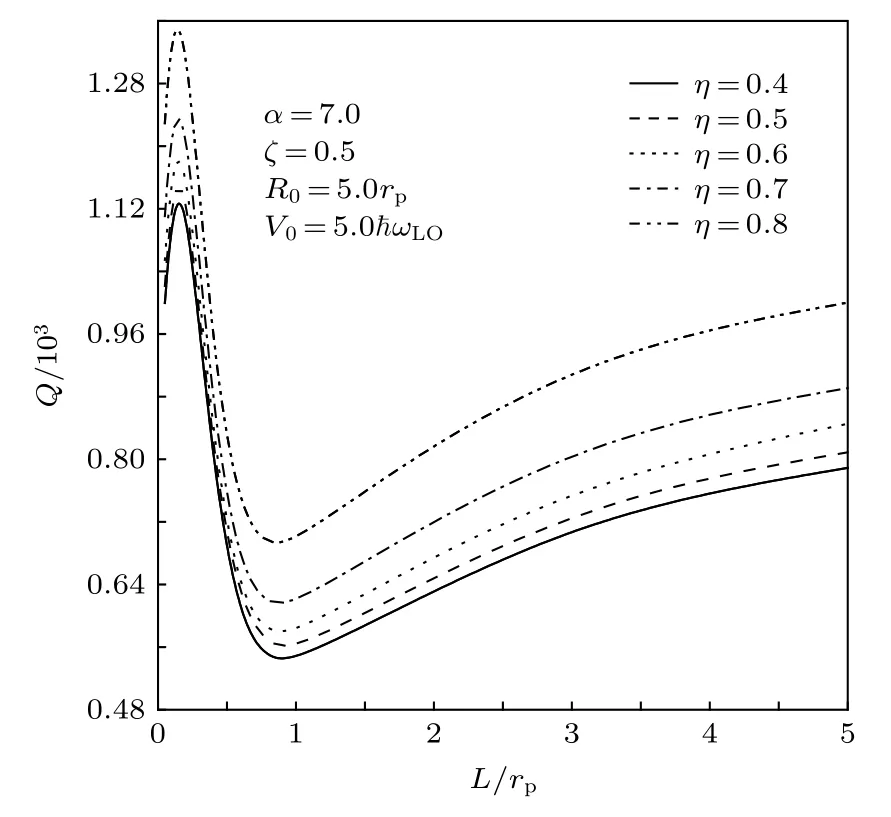
图9 相位品质因子 Q 在不同介电常数比 η 下随高斯势阱宽L的变化Fig.9.Quality factors of phase rotation Q as a function of the well width L of the AG potential at different the DC ratio η .

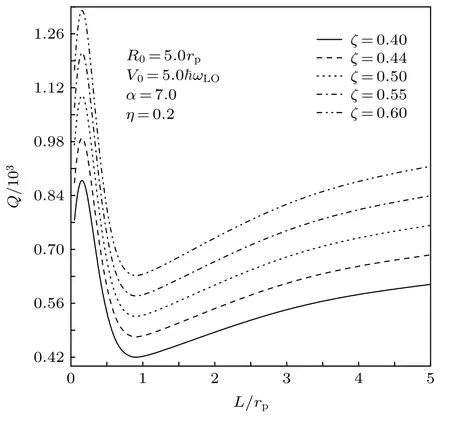
图10 相位品质因子 Q 在不同色散系数 ς 下随高斯势阱宽L的变化Fig.10.Quality factors of phase rotation Q as a function of the well width L of the AG potential at different dispersion coefficient ς .

4 结 论

选用双参量非对称高斯势描写量子点中电子的受限能够更好地反映量子比特的量子化特性.介质的色散系数、介电常数和电声耦合强度对量子比特的形成和信息存储有利有弊.提高材料的色散系数或介电常数比不仅有利于量子比特球的相位旋转操控, 也有利于改善量子点量子比特的相干性.本文的结果对从事制备和操控量子点量子比特的相关实验工作提供借鉴.