基于聚焦离子束纳米剪纸/折纸形变的三维微纳制造技术及其光学应用*

陈珊珊 刘幸 刘之光 李家方

1) (北京理工大学物理学院, 教育部先进光电量子结构设计与测量重点实验室,北京市纳米光子学与超精密光电系统重点实验室, 北京 100081)

2) (中国科学院物理研究所光物理重点实验室, 北京 100190)

特邀综述

1 引 言

剪纸艺术是我国古老的传统民间艺术瑰宝, 以一把剪刀, 一张薄纸, 即可传递创作者的美好寓意.其发展源头可追溯到《史记》中所记载, 西周初期周成王(公元前1055—1021年)将梧桐叶剪成“圭”状作为信物赐其弟并封侯, 史称“桐叶封弟”[1].自东汉蔡伦于公元105年改进造纸术后, 纸张开始普及, 符合民情风俗的剪纸艺术便随之在民众中产生[2].目前中国发现最早的剪纸文物是公元386—581年期间的“北朝对马团花剪纸”[1], 其复原图的精妙及复杂程度令人惊叹, 如图1所示.随着时代更迭, 具有自身独特魅力的剪纸艺术被视为民族文化中的一块活化石流传至今.

然而, 早期的人们并没有关注到剪纸艺术中所包含的科学思想, 直到剪纸文化于公元6世纪传播到日本后[3], 才被人们作为一门独特的技术得到详细的记录和不断的发展, 形成更为丰富的表达形式和科学延伸[4].在西方, 剪纸和折纸最早是作为仪式的象征符号独立发展起来的, 并于15世纪作为礼物、装饰、艺术品等在社会名流间盛行起来.1962年Florence Temko根据剪纸的日语发音(kiri意为“剪”, gami意为“纸”), 在书籍《Kirigami,the Creative Art of Papercutting》中用“kirigami”一词命名剪纸并被广泛使用[5], 与剪纸相对应的还有折纸艺术的英文名称“origami”, 同样源于日语(ori意为“折”), 导致很多学者认为剪纸艺术起源于日本.需要说明的是, 剪纸分为图形剪裁和结构形变两步, 而折纸一般不包含剪裁部分, 为介绍方便, 在本文中统称这两类技术或方法为剪纸.

自2010年以来, 剪纸技术作为一种新颖的三维加工方式被广泛应用于机械、医疗、微电子、声学、光学等领域[6-12], 并在各个空间尺度得到了开拓性的发展, 比如外太空飞行器的太阳能帆板折叠技术[10]、微纳机电系统[7]、生物医学设备[12]以及微纳米级机械和光子材料[6,8,9,13,14].而随着现代材料和制造领域的飞速发展, 剪纸技术近年来在三维微纳加工领域也具有较大的发展空间[15-18].这项技术无需多层平面堆叠工艺所要求的精准拼接[19],也不需要三维激光制备过程中的三维精确平移[20,21],就能实现从二维平面图形到三维立体结构的丰富形变, 所制备的结构在连续性、复杂性、几何构造演化、动态调谐等方面显示出独特的优势[7].

在微纳尺度实现剪纸形变的手段主要分为应力控制形变和机械引导形变.其中应力控制的折叠、弯曲等现象本质是利用不同应力作用到不同区域, 为达到最后的应力平衡使得结构发生形变.因此要实现预期的结构形变, 关键是要对结构施加合适的应力.而针对环境和材料的差异, 在微纳尺度结构上施加应力的方法可分为毛细作用力[22-26]、薄膜残余应力[27-30]、主动材料法[31-36]等, 如图2(a)所示[16].例如, 对于不同材料堆叠而成的多层薄膜,当用腐蚀等方法移除底部的牺牲层后, 悬空的结构因残余应力的存在会发生自行卷曲形变(图2(c))[28,37];对于主动材料, 通过改变温度、湿度等参数, 可以使结构产生空间上的非均匀应力分布, 从而使二维图案形变得到三维结构(图2(d))[32,38].此外, 通过对结构进行拉拽等机械手段也可实现对形变的精确控制, 得到复杂的三维结构.例如, 2015年张一慧课题组[39]先在衬底上做好预先设计的二维图案,再转移到一张预拉伸的衬底上进行局部固定, 衬底被释放后发生收缩, 导致二维图案隆起形成复杂多样的三维结构 (图2(e)).同年, Blees等[13]将石墨烯裁剪成各种典型的剪纸结构, 利用机械探针、激光诱导或磁场调控等方法, 完成了石墨烯从二维到三维的剪纸形变过程, 如图2(f)所示.最近, 高鸿钧课题组[40]在低温下利用扫描隧道显微镜操纵石墨烯, 可沿任意方向对石墨烯纳米岛进行反复折叠和伸展, 最终成功将石墨烯加工成原子级精确度的复杂“折纸”结构(图2(g)).

由此可见, 利用剪纸/折纸形变构筑新的结构正逐渐形成一个独特的研究领域, 但在微纳尺度,这类研究还面临诸多挑战.这是因为, 以往的在微纳尺度上的剪纸/折纸技术, 首先要预先设计好结构形貌和应力施加方案, 再经过一系列不可逆的工序形成微纳结构, 中间步骤很难修改、添加或删除.因此实现片上、原位、可控的三维纳米剪纸成了很多科研学者追求的新目标.基于前期的探索工作[41,42],为展现纳米剪纸在三维微纳加工方面的卓越能力及其应用潜力, 为国内同行提供一定的研究参考,本文着重介绍和总结基于聚焦离子束(focused ion beam, FIB)辐照的纳米剪纸加工原理、技术及其应用.对以往的基于FIB折叠/弯曲的研究工作(即下文的“树型”纳米剪纸)进行总结, 重点介绍了近期发展的基于结构拓扑形貌引导的纳米剪纸概念(即下文的“闭环”纳米剪纸), 并采用这两种类型的加工方法制备几何形貌丰富的三维微纳结构.更重要的是这些纳米剪纸结构具有的独特光学效应,如多重法诺(Fano)共振及其强耦合作用, 超光学手性, 超构表面衍射、相位和偏振特性以及光子自旋霍尔效应 (photonic spin Hall effect, PSHE)等.这些研究及制备的纳米结构可以为发展多功能三维制造技术(如三维纳米智能制造、新型4D打印等)、表面等离激元光学、纳米光子学、光力学、微纳机电系统等提供新的技术支持和研究思路.

2 基于聚焦离子束的三维纳米折叠/剪纸

制造技术的微纳米尺度化赋予了微观结构新的物理特性, 伴随着人工微纳结构领域的迅速发展和微纳器件应用需求的不断提高, 微纳制造技术向三维空间扩展成为一种必要和必然的趋势.然而,传统的自上而下和自下而上的半导体工艺、纳米颗粒自组装技术, 以及三维激光直写等技术, 遵循的是一种线性序列, 大部分通过逐层加工二维平面来堆叠三维空间或三维逐点加工构建立体结构, 工艺的复杂度和结构复杂程度成正比.而将FIB作为加工手段引入到三维纳米折叠/剪纸技术中来, 可形成独特的从二维平面到三维立体结构的形变科学, 从而突破传统三维微纳制造的线性累加思维,在结构的连续性、复杂性、几何构造演化、动态调谐等方面显示出巨大的发展空间和应用潜能.本节首先从原理和应用两部分对FIB纳米剪纸技术进行简单介绍, 进一步深入讨论利用FIB所构建的纳米剪纸的类型以及结构变形的不同特性.

2.1 聚焦离子束微纳加工简介

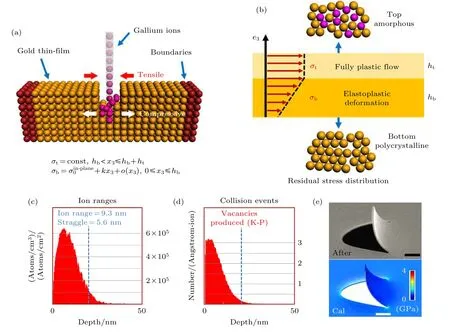
图3 基于FIB辐照产生应力的主要机理[43] (a), (b)自支撑金膜在FIB辐照下的应力分布和双层应力模型示意图; 利用SRIM软件计算得到的在加速电压为30 kV时(c)镓离子和(d)空隙的深度分布图; (e)舌型结构在FIB全局辐照后的扫描电子显微镜 (scanning electron microscopy, SEM)图像和利用 (b)图中双层应力模型计算的结果 (比例尺：1 µm)Fig.3.Illustration of the fundamentals of FIB-induced stress[43]：(a), (b) Schematic illustration of residual stress distribution and double-layer stress model within a gold nano-film under FIB irradiation; simulated distributions of (c) gallium ion concentration and(d) vacancy density versus the depth of the nanofilm using SRIM software with ion acceleration voltage of 30 kV; (e) SEM image of a tongue-like structure after FIB global irradiation and the calculated result (Scale bars：1 µm).

FIB系统中液态金属离子源产生的离子经过高压抽取和加速后, 可通过电透镜和偏转透镜照射到样品表面的指定位置, 在撞击过程中可剥离样品表面的原子达到切割或研磨的目的, 最终实现微纳米结构的加工.文献[43]中, 基于FIB纳米剪纸的主要工具是标准的FIB刻蚀系统, 即一台双光束FIB/SEM 系统 (FEI Helios 600i), 其液态离子源为镓 (Ga)离子, 加速电压为 8—30 kV, 束流从24—80 pA (实际上, 纳米剪纸的必要条件是获得一定形式的应力分布, 在具体设备方面具有通用性.实验结果表明, 其他形式的离子源, 如氦离子源刻蚀系统, 也能够实现类似的功能).长久以来,FIB作为一种纳米加工手段, 在使用的过程中往往伴随着残余应力、表面损伤、离子注入等难以避免的现象.而纳米剪纸方法却正是充分利用这种由镓离子和金膜碰撞而产生的“不希望的”残余应力来改变样品的表面形貌, 实现微纳米结构的直接无掩模加工[43].具体来说, 如图3(a)所示, 当金纳米薄膜(本文中为自支撑的金纳米薄膜, 厚度为80 nm[43])受到高能离子束照射时, 会发生若干物理过程, 主要过程可总结为以下四方面[43,44]：1)一些金原子被溅射离开表面从而产生空隙, 剩余的金原子发生颗粒聚合[45,46], 导致在薄膜表面附近产生张应力;2)一些镓离子被注入到金膜内部, 产生压应力;3)镓离子的撞击使得一些未被溅射出的金原子发生位移; 4)金原子和镓原子发生再沉积现象.SRIM软件可用于模拟预测空隙和注入的镓离子的范围[43].如图3(c)和图3(d)所示, 在 30 kV 电压下, 加速的镓离子撞击到金膜上, 使在接近表面的20 nm范围内存在注入的离子和产生的空隙.即FIB对一定距离的金膜影响较大, 但底层金膜几乎不受直接影响.用图3(b)中的双层应力模型来描述在离子束辐照下金膜的受力分布情况[43].考虑到表层金膜受各种物理过程的综合影响且受直接影响的厚度很薄(＜ 20 nm), 可用一个均匀分布的等效张应力进行描述.而底层金膜主要因为表层金膜间接带动发生弹性形变, 因此具有从上到下的梯度应力.在该模型中, 由于张应力占主导地位,于是受到FIB全局辐照后的舌型结构向上弯曲,如图3(e)所示[43].理论计算出的结果与实际的弯曲完全一致, 充分说明该模型的准确性.

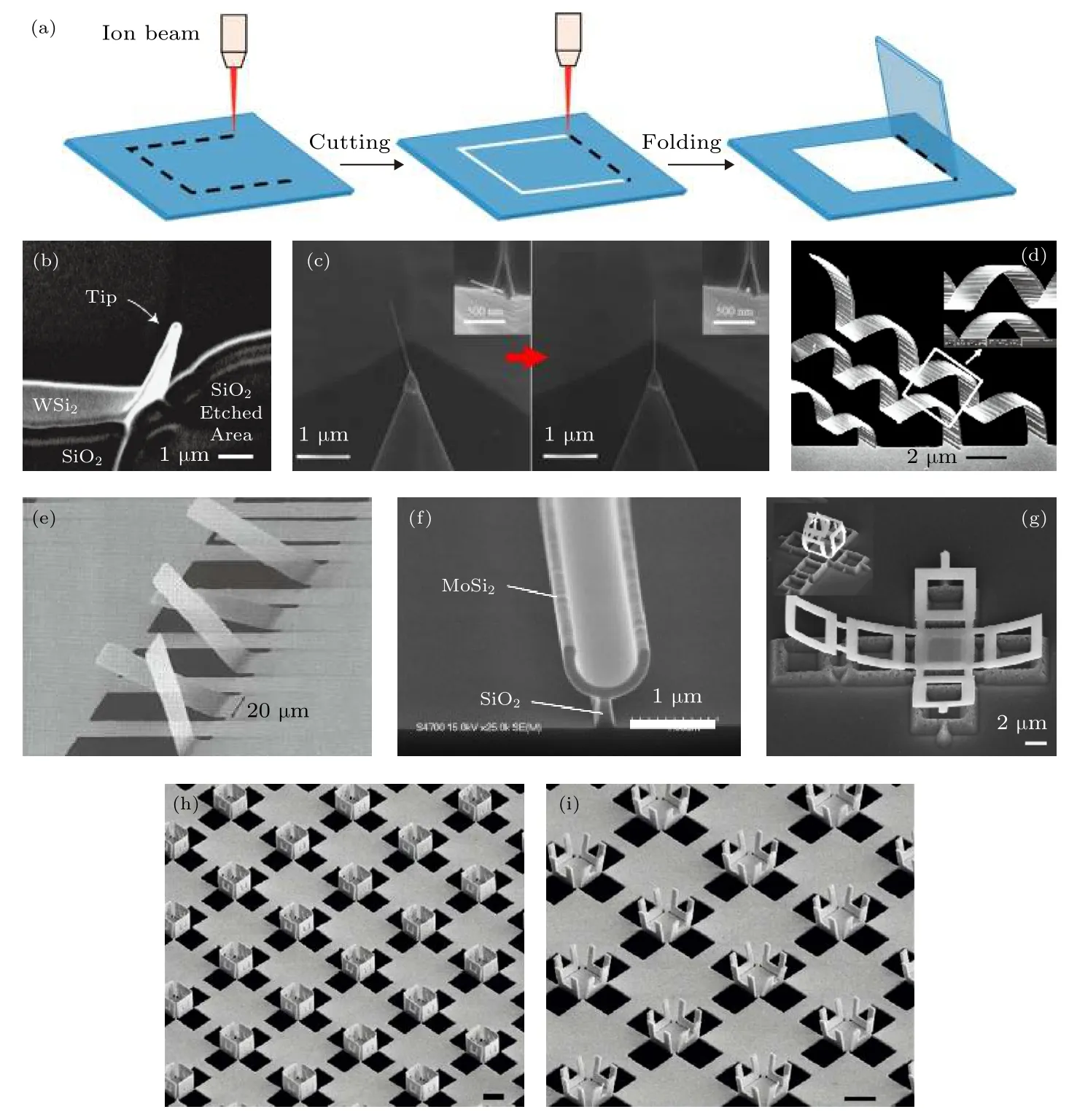
图4 (a)离子束剪裁、折叠悬空纳米薄膜示意图; (b)—(i) FIB 制备的各种三维结构的 SEM 图像[49—52,54,55,57]Fig.4.(a) Schematic illustration of ion beam cutting and folding of thin film; (b)-(i) SEM images of various 3D structures prepared by FIB[49-52,54,55,57].

自20世纪80年代离子束系统被成功应用于半导体行业以来, FIB技术已成为亚微米制造和无掩模工艺的有效方法之一[47,48].在利用FIB进行实际的纳米加工过程中, 人们发现经过扫描的一些地方会意外出现缺陷、损伤或不良应力, 因此, 人们在使用FIB时通常都要尽量避免额外的离子束扫描.然而, Yoshida等[49]将这一缺点充分利用起来, 在2005年展示了FIB导致纳米结构弯曲的现象 (图4(b)).接下来, 2006年Park 等[50]利用 FIB实现了碳纳米管的弯曲(图4(c)); 同年北京大学吴文刚课题组[51]使用该方法在悬空薄膜上制备出了三维螺旋(图4(d))和立方框架结构; 2007年麻省理工学院Arora等[44,52]系统地研究了基于FIB的三维形变折叠工艺(图4(e)).这些研究表明, 自支撑薄膜上的FIB辐照可以使得纳米结构发生折叠和重组[37,50,51,53-60], 如图4(f)—(i)所示[54,55,57], 意味着FIB有可能成为纳米尺度剪纸形变过程的“纳米手”.但由于缺乏实际应用, 该技术在随后的数年里发展缓慢.直到2015年中国科学院物理所微加工实验室崔阿娟等将该技术首次应用于构建近红外波段的三维超构材料[57], 如图5(a)和图5(b)所示, 展示了该方法在光学波段的首次应用, 从而激发了大家利用该技术发展光学应用的极大兴趣,陆续制备出具有多重Fano共振[58,60,61]、光的选择性传输(图5(c))[62]、中红外光开关 (图5(d))[59]、环偶极子共振(图5(e)和图5(f))[60,63]等优异光学性能的三维微纳结构.然而, 所有这些方法以及它们的应用都未提出或论证“纳米剪纸”的概念.这主要因为此类折叠过程比较简单, 人们可以轻易预测折叠产生的结构效果, 无需引入其他概念; 同时, 大家在这类研究中采用的依然是一种串行的线性加工思维, 即结构各形变部位之间相互独立, 与剪纸加工思维大相径庭.

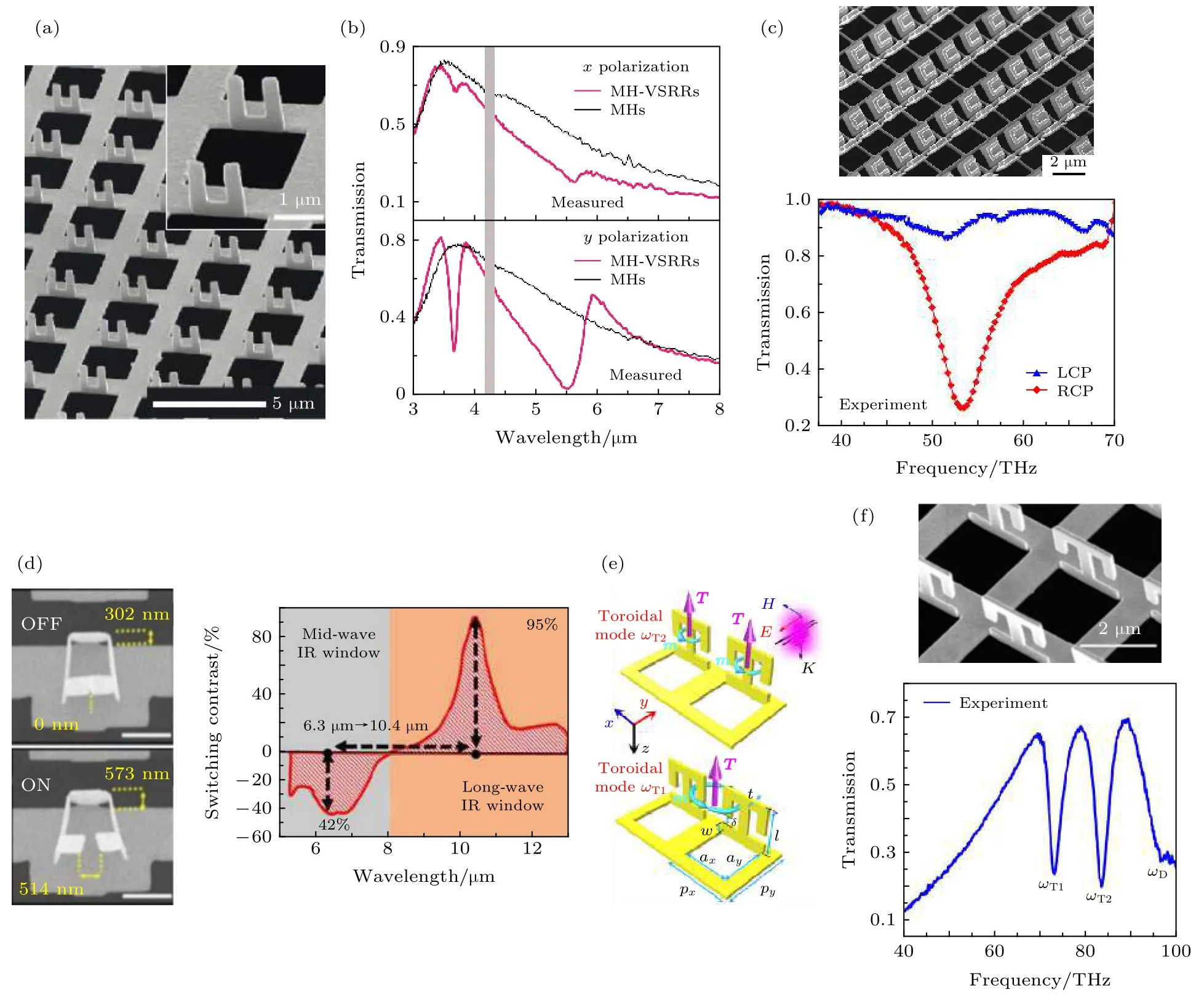
图5 (a), (b) 垂直开口谐振环 (VSRR)与金属矩形孔组成的复合结构 (MH-VSRR)阵列及其偏振相关 Fano 共振[57]; (c)三维折叠超表面的SEM图像以及右旋圆偏振光(RCP)和左旋圆偏光(LCP)的透射光谱[61]; (d)可调的三维SRR分别处于OFF和ON态时的SEM图像, 及纳米SRR阵列的开关光谱特性[59]; (e)环形偶极子模式的示意图[63]; (f)三维超材料SEM图片及透射图光谱[63]Fig.5.(a), (b) Composite structure (MH-VSRR) prepared by FIB and the polarization-dependent Fano resonance[57]; (c) SEM image of 3D folded metasurface and experimentally measured transmission spectra under illumination of different circularly polarized waves[61]; (d) SEM images of switchable 3D SRR[59] in OFF and ON states at currents of 0 and 20 mA, respectively, and corresponding switching spectra; (e) schematic of toroidal dipole modes generated due to circulating magnetic field produced by current loops[63]; (f) SEM image of the 3D toroidal metamaterial and the measured transmission spectra with toroidal dipole resonance dips[63].

2.2 基于聚焦离子束的纳米剪纸技术

2018年, 我们在前人工作的基础上, 设计出一类新的二维图案, 采用高剂量的FIB对自支撑的金纳米薄膜进行刻蚀(即“剪裁”), 随后利用低剂量的FIB进行全局辐照, 使结构在图案拓扑形貌的引导下实现三维纳米结构力学“形变”[43].特别是在连续的三维形变过程中, 纳米结构的原位折叠、屈曲、旋转和扭曲明显具备了宏观剪纸的本质特征,并具有优于50 nm的分辨率, 因此将其命名“纳米剪纸”[43], 并成功地确立了基于FIB“纳米剪纸”三维微纳加工的概念[42].

2.2.1 纳米剪纸的分类

在纳米剪纸结构从二维向三维变形的过程中,具体的形变形式与程度除了受加速电压、扫描模式与剂量的影响(图6)外, 还与结构本身的拓扑形貌有莫大的关系.根据动力学系统的拓扑分类概念,从结构拓扑形貌角度, 可以将纳米剪纸分成“树型”(tree-type) (也称为“开环”(open-loop))和“闭环”(close-loop)型[64,65].

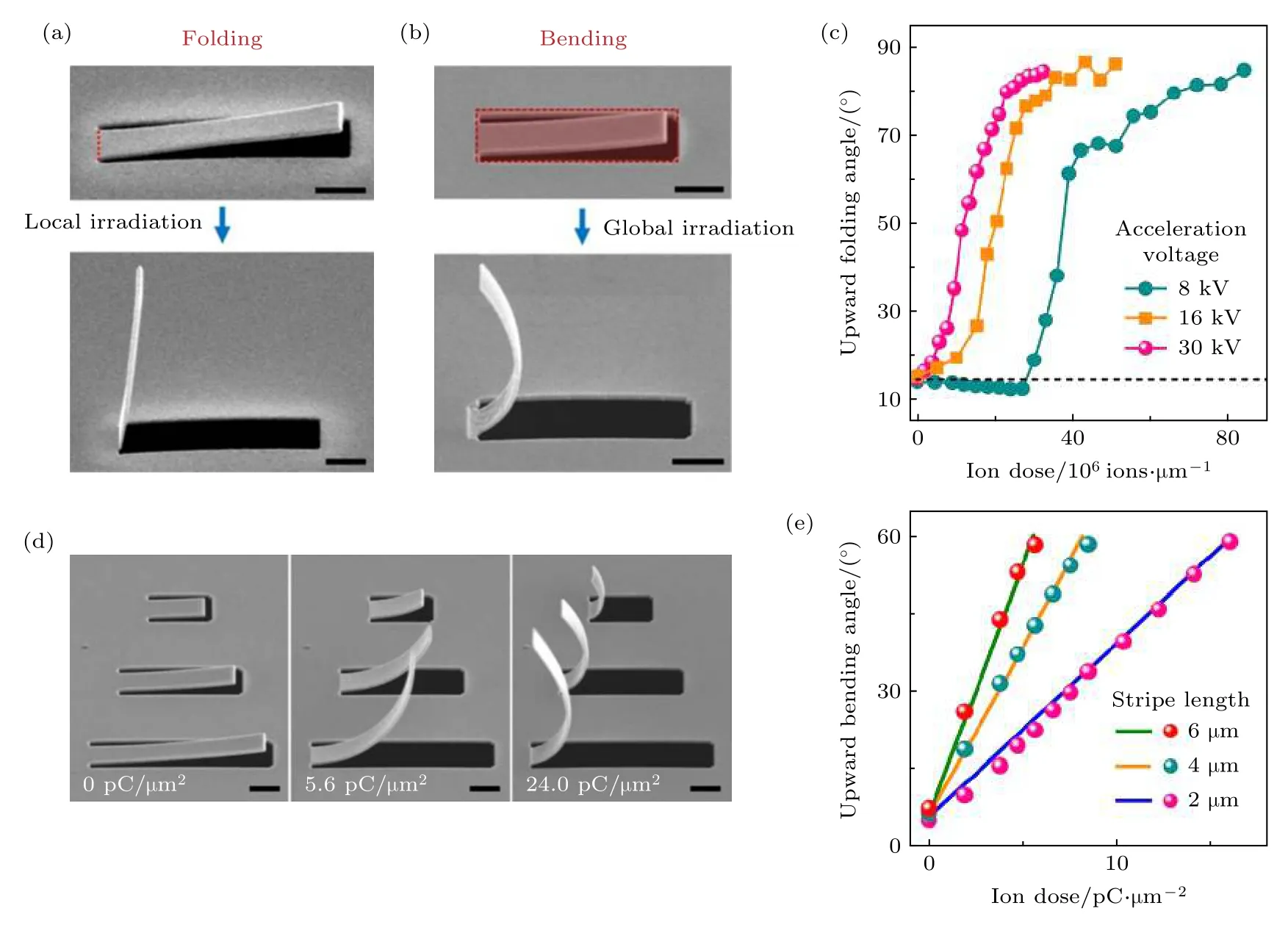
图6 (a) FIB局域扫描红色虚线、折叠悬臂的SEM图[42]; (b) FIB全局辐照红色虚线框内区域导致悬臂向上弯曲的SEM图[42];(c)测量得到的不同加速电压下悬臂梁折叠角与扫描剂量的关系[43]; (d)不同尺寸的悬臂在不同剂量FIB全局扫描下弯曲的SEM图像[43]; (e)测量(点线)与计算(实线)得到的在加速电压为30 kV时不同长度悬臂梁的折叠角与扫描剂量的关系[43](比例尺：1 µm)Fig.6.Side-view SEM images of (a) rigid folding and (b) gradual bending of suspended cantilevers under local and global FIB irradiations, respectively, over the red areas [42]; (c) measured relationship between the cantilever folding angle and the scanning dose at different acceleration voltages[43]; (d) SEM images of different sizes of cantilever bending under FIB global irradiation with different dose[43]; (e) measured (dotted line) and calculated (solid line) relationship between the folding angle and the scanning dose at acceleration voltage of 30 kV[43] (Scale bars：1 µm).

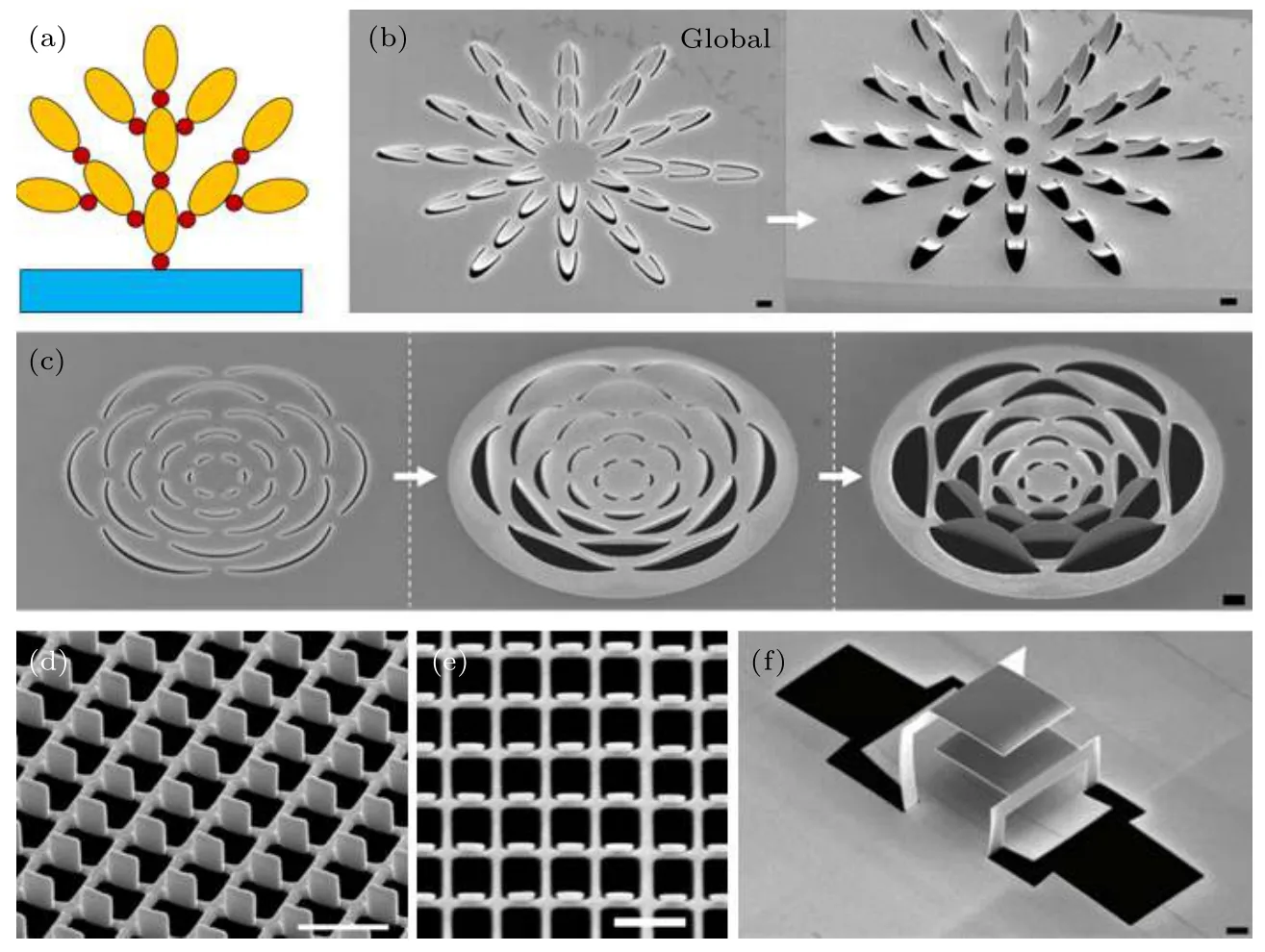
图7 “树型”纳米剪纸 (a)“树型”-纳米剪纸结构示意图; (b)—(f)“树型”纳米剪纸结构 SEM 图像, 其中 (b), (c)为由 FIB 全局辐照得到的两种花瓣型结构[42,66]; (d)(f)为由FIB局域辐照得到结构的SEM图片, (d), (e)垂直矩形板阵列的侧视图和俯视图[42];(f)多层平板结构[42](比例尺：1 µm)Fig.7.Tree-type nano-kirigami：(a) Schematic of tree-type system; (b)-(f) SEM images of typical examples of 3D tree-type nanokirigami.(b), (c) Flower-like structures obtained by FIB global irradiation[42,66]; (d), (e) side-view and top-view of vertical plates standing along one edge of the planar metallic hole arrays[42]; (f) multilayer plate structure[42] (Scale bars：1 µm).

图8 “闭环”纳米剪纸[42,43] (a)“闭环”纳米剪纸结构示意图; (b)-(d)由FIB局域辐照下“闭环”纳米剪纸得到的三维纳米结构的SEM图像[42]; (e), (g), (i)宏观纸质剪纸结构照片及与其对应的(f), (h), (j)通过FIB全局扫描“闭环”纳米剪纸得到的三维纳米结构的 SEM 图像[43] (比例尺：1 µm)Fig.8.Close-loop of nano-kirigami[42,43]：(a) Illustration of the close-loop system; (b)-(d) SEM images of 3D nano-kirigami with local FIB irradiation[42]; (e), (g), (i) camera images of the macroscopic paper kirigami; and (f), (h), (j) corresponding microscopic structures reproduced by close-loop nano-kirigami with global FIB irradiation[43] (Scale bars：1 µm).

在变形过程中, 树型结构的子结构都是相对独立的个体, 不会对其他模块产生太大影响.图7(a)是“树型”纳米剪纸结构的示意图, 黄色椭圆代表剪纸结构中的子结构, 红色圆形表示连接区域.当其中一个子结构受外力作用发生形变时, 存在两种不同的情况：若变形结构位于末端, 则不会影响其他部分; 若前端结构变形, 与之相连接的下级结构会受前端结构影响而发生变化, 但这种变化属于线性传递过程, 相对位置不会发生变化.

图9 各种形貌奇特的三维纳米剪纸结构在FIB全局扫描前后的顶视或侧视SEM图[43] (a) 斐波那契双螺旋结构; (b), (c)窗花互连型纳米栅栏; (d)不同剂量FIB辐照前后的螺旋结构; (e)双层螺旋异质结构(比例尺：1 µm)Fig.9.Top-view and side-view SEM images of typical structures before and after global FIB irradiation[43]：(a) A twisted triple Fibonacci spiral; (b), (c) window-decoration type nanobarriers; (d) a deformable spiral; (e) a double-layer spiral structure (Scale bars：1 µm).

除了形变的拓扑形貌分类外, 纳米剪纸可按FIB辐照方式分成两类, 一种是对样品局部进行区域扫描的局域扫描模式(图6(a))[42], 另一种是对样品整体区域进行扫描的全局扫描模式(图6(b))[42].局域扫描模式中薄膜材料只发生单一角度的折叠,容易受遮挡效应的限制; 全局扫描则可以让薄膜发生连续的曲率变化, 使结构发生整体性的形变.例如, 在“树型”纳米剪纸方法中, 通过合理地运用全局扫描(图7(b)[66]和图7(c)[42])或局域扫描(图7(d)—(f))[42]方式, 可以让FIB按设计好的顺序扫描特定的区域而弯曲或折叠纳米结构, 形成具有各种几何形状的三维结构.这种方法由于结构在不同分支之间的形状变换是相对孤立的, 非常适合加工具有规则几何形状的纳米结构阵列, 如图7(d)和图7 (e)[42]所示.事实上, 这种用FIB产生的“树型”折叠或弯曲自2006年以来已经在多个研究工作中得到体现[44,45,51,52,55,57-60,67,68].只是由于它们与传统的立体剪纸形变方法相比相对简单, 没有被意识到剪纸的概念, 为方便该领域工作的总结与介绍, 这里我们也将其归入“树型”纳米剪纸的范畴.

与树型结构各形变部位之间相互独立不同, 各部位互相关联、嵌套的加工思路归属于“闭环”类型.如图8(a)所示, 若离子束照射中间的子结构使其发生形变, 与之相连的结构都会受到影响而发生形变, 且形变的类型和程度均不相同, 最终导致整体结构都会发生变化.这种单元形变相互关联的特性充分体现了立体剪纸的内在本质, 乃至可为四维制造提供额外的自由度[15].这种特性的发现是十分有意义的, 虽然在宏观世界已经广泛地应用于各领域, 但在纳米尺度并未得到足够的重视.为此,我们在这里重点论述基于FIB的“闭环”纳米剪纸概念.图8(b)—(d)展示的是在FIB局域扫描模式下得到的一些复杂三维结构的闭环折叠[42].可以看到并未受到FIB直接辐照的部分也发生了“被动”变形, 反映了闭环结构的固有特征.相较于局域扫描, 全局扫描纳米剪纸技术可以诱导更先进的闭环纳米结构, 可以实现连续曲率变换, 生成各种前所未有的三维特异结构(如图8(f)、图8(h)、图8(j)和图9所示)[43].图8(e)—(j)是一些典型的宏观剪纸结构和利用FIB全局辐照的闭环形变得到的相应的三维纳米结构[43].可以看到, 纳米剪纸将宏观剪纸尺寸缩减到1/10000, 实现了高可塑性和高精确度的三维微纳加工, 为结构的设计和进一步研究提供了新颖的研究平台.

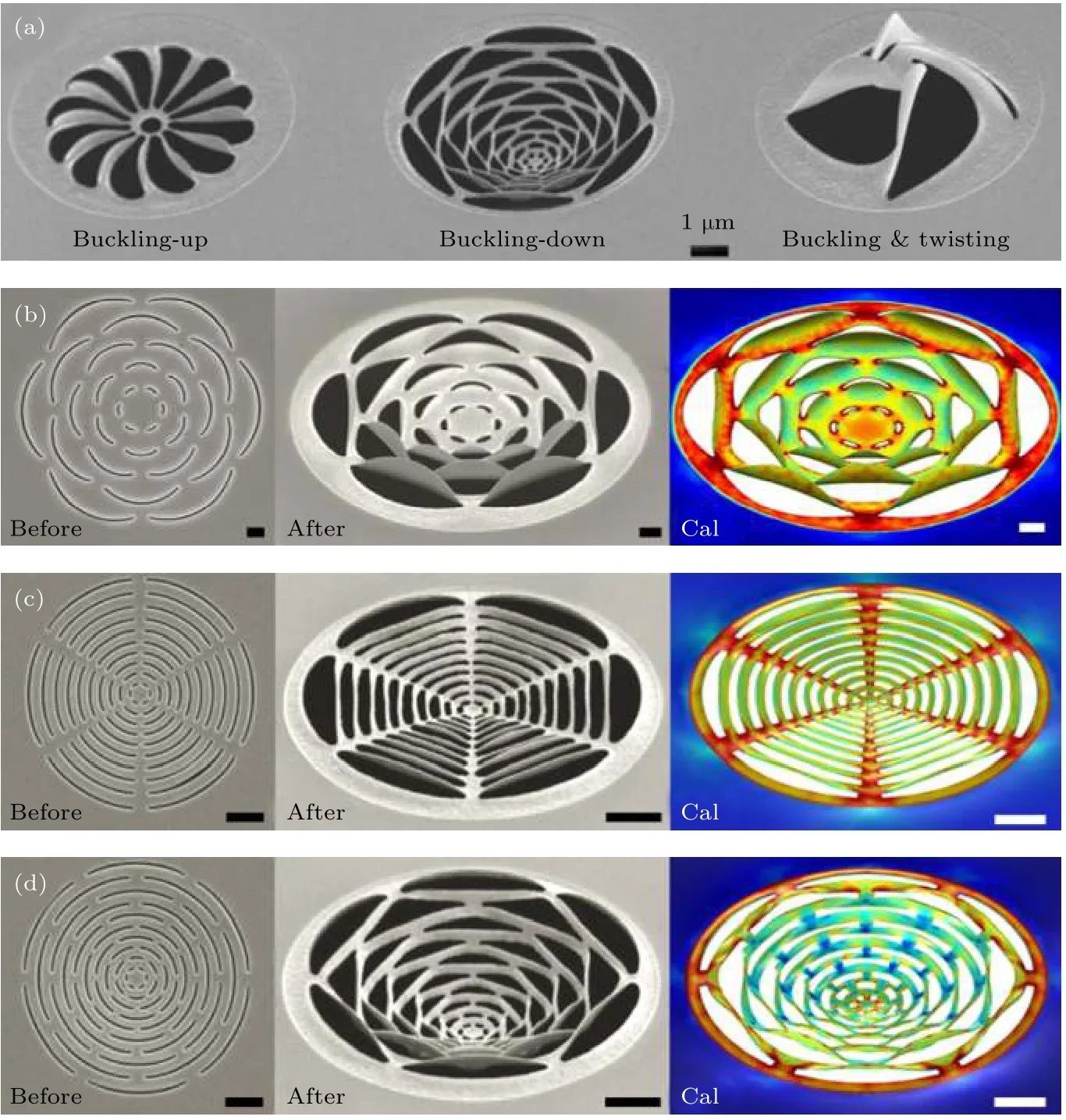
图10 “闭环”纳-米剪纸的形变特性[43] (a)叶片结构、可扩展网状结构和四臂风车结构在其二维前体受到相同FIB全局辐照后的SEM图像; (b)(d) FIB全局辐照前后的二维前体和对应的三维结构以及数值模拟的应力形变结果, 其中 (b)花型结构,(c)蛛网结构, (d) 可扩展网状结构 (比例尺：1 µm)Fig.10.Feature of “closed loop” nano-kirigami[43]：(a) SEM images of a blade structure, expandable web and four-arm windmill fabricated together after the same global FIB irradiation; (b)-(d) SEM images of different web structures (left) before and (middle)after FIB irradiation; (b) a flower-like structure; (c) a spider web—like structure; (d) an expandable web structure; the simulation results after nano-kirigami is shown on the right (Scale bars：1 µm).

2.2.2 纳米剪纸的形变特性

纳米剪纸结构具有丰富的形变特性, 例如, 在拓扑形貌的引导下, 不同的二维图案在向三维转换的过程中发生形变的方式和程度不尽相同.图8中(f)图的可扩展网状结构、(h)图的叶片螺旋结构和(j)图的四臂风车结构在其前体二维图案受到相同的FIB向下的全局辐照时, 分别发生了向上屈曲、向下屈曲以及向上的屈曲和扭转的综合变形, 如图10(a)所示[43].即使对于同一类形状, 子结构的尺寸、间距等因素也会影响形变效果.而且,即使形变方式相同, 形变程度也会不一样.图10(c)中的蛛网结构和图10(d)中的可扩展网状结构在受到相同的FIB辐照时, 均向下屈曲, 但蛛网结构的形变幅度明显小于可扩展网状结构[43].在图11(a)和图11(b)可以更清楚地看到, 网状结构的深度达到 740 nm 时, 蛛网结构才向下屈曲了 218 nm[43].而且由于蛛网结构的径向连接部分受到的应力远大于其他位置, 而可扩展网状结构中的应力分布较为均匀, 因此当FIB扫描剂量增加到某个临界值时, 蛛网结构会先于可扩展网状结构发生破裂, 如图11(c)所示[43].

三维纳米形变的不确定性给我们的结构设计带来一定的挑战, 但正是这种丰富的形变特性为各种新颖三维结构的设计和制备带来无限可能.而且可以看到数值模拟结果与实验结果几乎完全一致,表明人们可以通过精确的预测设计为实验研究奠定基础.需要指出的是, 这些纳米精度的、截然不同的形变方向、形变程度, 以及其原位、实时的加工特性, 是其他微纳加工方法所无法实现的, 体现了纳米剪纸所独有的优势.

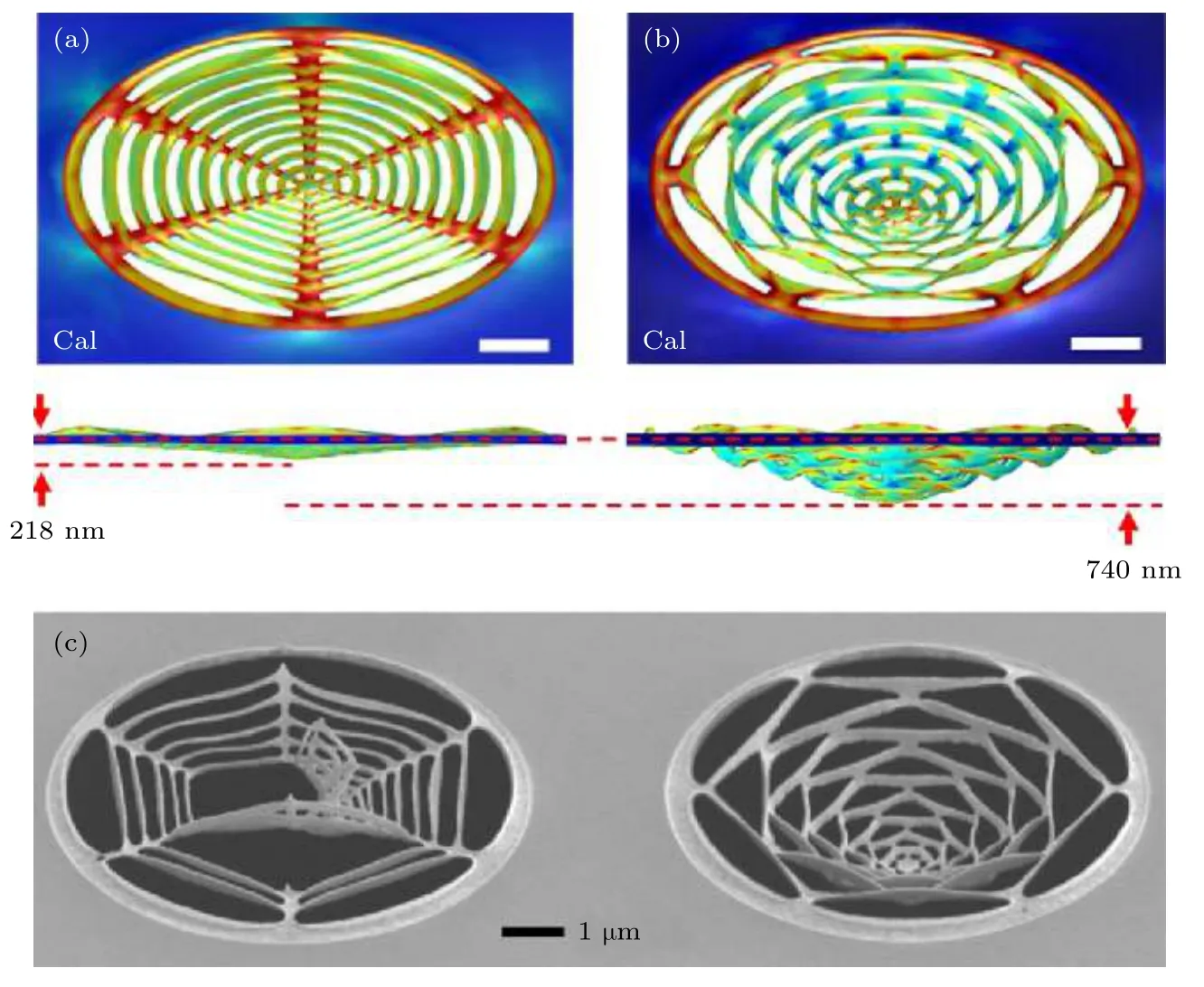
图11 数值模拟对结构形变的精确预测与额外信息获取[43] (a), (b)数值模拟蛛网结构和可扩展网状结构在相同FIB辐照下受力形变的侧视图和前视图, 其中不同的颜色代表受到不同强度的应力, 红色区域承受的应力最大(比例尺：1 µm); (c)两种结构承受相同FIB扫描后的SEM图Fig.11.Additional information from numerical simulation for the accurate prediction of structural deformation[43]：(a), (b) Side and front view of the deformation and stress distribution of the spider web-like and the expandable web structure under the same initial stress in simulations; the different colors represent stresses of different strengths, and the red areas are subjected to the highest stress (Scale bars：1 µm); (c) SEM image of the two web structures after the same high-dose FIB irradiation.

3 纳米剪纸三维结构的光学特性

3.1 法诺共振

基于FIB的“树型”纳米剪纸在过去十年中受到了一定的关注, 但大多数研究都将其潜力集中在形状转换或机械应用上.在光学方面, 崔阿娟等在2015年首先研究由竖直开口谐振环与平面金属孔组成的阵列结构(MH-VSRR阵列结构)的光学特性(图12(a)和图12(b))[57], 之后通过利用它们之间独特的三维电导耦合机制[58], 成功激发了其在近红外波段显著的且具有鲁棒性的Fano共振.为了实现Fano共振之间的强耦合, 我们利用FIB设计由图12(c)所示的非对称(两臂不等高) MH-VSRR阵列单元排列组成的阵列结构, 让共振模式一分为二, 形成两个独立的共振模式, 进一步通过模式之间的耦合作用, 在单一结构体系中得到三重Fano共振F1、F2和F3, 并清楚地观察到了Fano共振间的强耦合作用(表现为拉比劈裂)(图12(d)—(f))[60].另外, 通过使用基于 FIB的“树型”纳米剪纸技术在金属孔两侧构建垂直双板结构(图13(a)),成功激发了具有二向色性的五重Fano共振[61].这对于探索类似系统中的基础物理、增强光与物质相互作用、光学传感与探测等方向[69]都具有重要的参考价值.

3.2 光学手征体

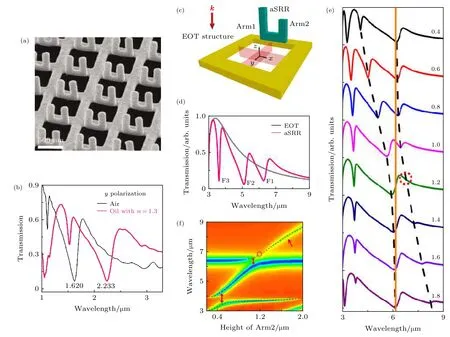
图12 具有 Fano 共振的“树型”纳米剪纸 [57,60] (a), (b)近红外波段 Fano 共振及超-灵敏折射率传感特性 [57], 其中 (a) MHVSRR阵列结构的SEM图及(b)测得的结构在空气和折射率为1.3的油中的透射谱; (c)(e)纳米剪纸结构中多重Fano共振间的强耦合作用[60], 其中(c)不对称MH-VSRR单元结构图及(d)结构所对应的透射光谱, 可以看到三重Fano共振F1, F2和F3;(e)固定左臂、改变右臂高度时MH-VSRR结构透射谱; (f)结构吸收谱与右臂高度的关系图, 理论和实验数据吻合得非常好Fig.12.Tree-type nano-kirigami structures with Fano resonances[57,60]：(a) SEM images of MH-VSRR[57]; (b) measured transmission spectra of the MH-VSRR array in air and oil; (c) schematic of the unit cell of a 3D asymmetric MH-VSRR[60]; (d) simulated transmission spectra of the asymmetric MH-VSRR array[60]; (e) simulated transmission spectra of the VSRR with the same left arm but variable right arm as noted; (f) colormap of the simulated absorption spectra versus the height of the right arm; the calculated(dashed lines) and measured data (stars) agree very well.

以上应用主要基于局域扫描模式的“树型”纳米剪纸结构, 与之相比, 全局扫描的“闭环”纳米剪纸技术构建的结构具有更丰富的三维弯曲和扭转特点, 为设计新颖三维光学结构提供了更多可能性.通过“闭环”纳米剪纸的扭曲形变, 可实现三维光学手征特性[43,66].手征特性是指一个结构没有任何镜面对称的特性, 即结构与其镜像不能通过平移、缩放和旋转等变换而重合的特性.自然界中存在很多具有手征特性的物体, 比如蛋白质分子、石英等.与在二维结构(指沿厚度方向结构没有变化)中观测到的外在光学手性[70,71]不同, 具有内禀手征特性的结构通常存在于三维结构中, 而人工微纳结构的光学手性响应相比于自然界材料高出好几个数量级[71-74].由于光学手性的物理根源是电极矩和磁极矩在平行方向上的交叉耦合[75], 所以具有扭转特性的三维结构(如螺旋结构)是实现强光学手征特性较为理想的结构类型.但纳米量级的三维螺旋结构制备起来比较困难, 很多高精度工艺如激光直写辅助电镀方法、FIB辅助沉积等需要严格的条件和娴熟的操作, 因此只有为数不多的几个课题组拥有这些技术; 同时, 这些方法在制备速度、材料选择、衬底选择、工艺兼容等方面存在一定的局限性.因此, 三维螺旋结构的研究工作局限在少数几个方面.我们将传统的螺旋结构垂直交叉并进一步演化变形, 设计得到一种三维风车结构,如图14(a)所示[43].当偏振方向沿x方向的线偏振光垂直入射时, 由于结构扭转, 电场分量Ex可以在x方向引起平行的电极矩px和磁极矩mx, 磁场分量Hy会激发沿y方向平行的电极矩py和磁极矩my, 而且感应电磁矩的方向高度依赖于风车结构四臂的左手 (left-handed, LH)或右手 (righthanded, RH)扭曲, 从而产生左手或者右手手性的光学响应, 如图14(b)和图14(c)中的第一列所示[43].图14(b)和图14 (c)中的第二列展示了不同手性结构的侧视图, 可以看到由于结构扭曲带来的等效环形电流以及产生的电极矩和磁极矩方向[43].由于光学手性取决于p·m的值[76], 所以相互平行的电极矩和磁极矩之间的强相互作用可以诱导产生非常显著的光学手性.图14(b) 和图14 (c)所示的风车结构在各个方向上的扭曲使得平行或反平行的电磁矩被引入并相互作用[72], 从而产生了较大的内禀光学手性[43].

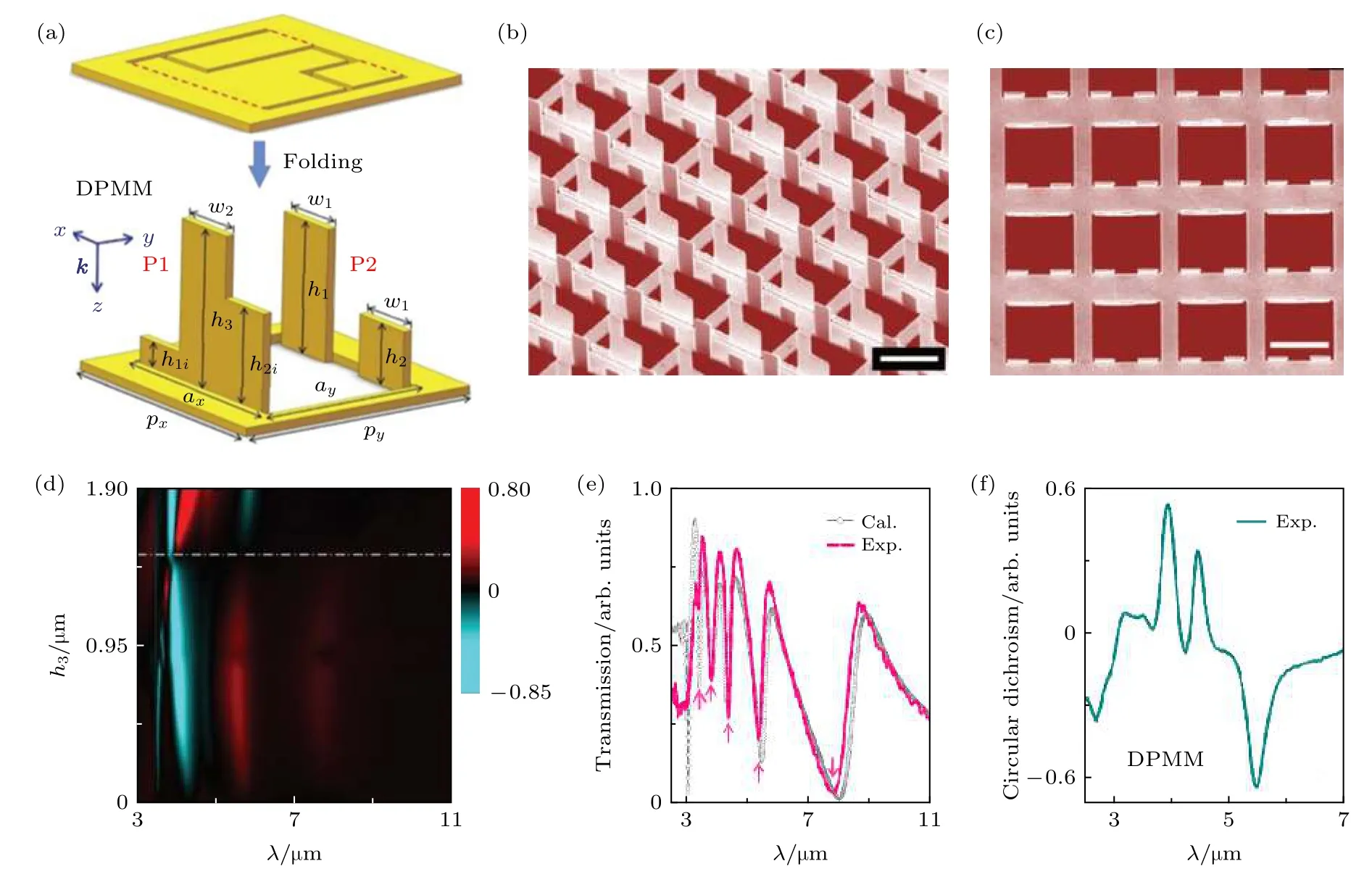
图13 具有超强圆二色性的五重 Fano共振[61] (a)基于竖直金属板的超材料 (DPMM)结构加工示意图; (b), (c) FIB局域扫描制备的DPMM 阵列结构的侧视和顶视SEM 图像(比例尺：2 µm); (d)模拟的DPMM阵列圆二色谱与h3的关系图; (e) h3取1.9 µm,y偏振入射时计算和实验得到的透射谱; (f)实验测量的h3取1.9 µm时的CD谱Fig.13.Five-fold Fano resonance with significant circular dichroism[61]：(a) Schematic diagram of the processing of DPMM; (b),(c) SEM images of DPMM structures prepared by FIB local irradiation (Scale bars：2 µm); (d) diagram of the relationship between CD and h3 of simulated DPMM; (e) calculated and experimental transmission spectra for the DPMM with h3 = 1.9 µm and y-polarized incidence; (f) experimental CD spectra of the DPMM in (e).

3.2.1 圆二色特性和圆双折射特性

从本质上讲, 纳米剪纸构建的三维风车结构由于打破了其形变前二维结构的镜面对称性而产生结构手性(LH或RH).而要获得光频波段的光学手性响应, 还要使同一结构对不同手性的圆偏振光具有不同的折射率(其差值可表示为χ=(nR-nL)/2).其中χ的虚部导致结构对左旋或右旋圆偏振光具有不同的吸收, 即产生圆二色性(circular dichroism,CD), 体现为透射光谱的差异;χ的实部导致二者产生相位差, 即圆双折射特性(circular birefringence,CB), 体现为对入射线偏振光的偏振旋转效应.图14(g)和图14(h) 表征了纳米剪纸结构光学手征特性的测量结果[43], 可以看到, 图14(e)中的二维结构没有任何圆二色性和圆双折射特性, 相比之下, 图14(f)中的三维风车结构则不仅有着明显的圆二色性, 而且表现出非常强烈的圆双折射特性.在大于阵列周期的波段, 垂直入射的线偏振光的偏振方向会出现明显的偏转, 随着波长增大偏振旋转的角度逐渐增大.波长在 1.7 µm和 1.95 µm处时,在保持线偏振态的同时其偏振方向分别偏转90°和 135°.三维风车结构整体的厚度约为 0.43 µm(包括衬底), 由圆双折射效应引发的线偏振方向偏转可达 310000°/mm, 如图14(h)所示, 超过已报道的手征超构材料和同类的二维平面纳米结构[43].其实验测量结果和数值模拟结果相吻合, 充分证明利用纳米剪纸技术实现的三维扭转结构可用于构建具有优异特性的光学超手征体.与在其他波段(THz、GHz、中红外)通过堆叠或扭转工艺设计的手性结构相比, 纳米剪纸技术不仅能够保证结构的复杂性, 还可实现简易、高精度的加工流程, 更重要的是, 结构的工作波长可被调节到近红外通信波段.

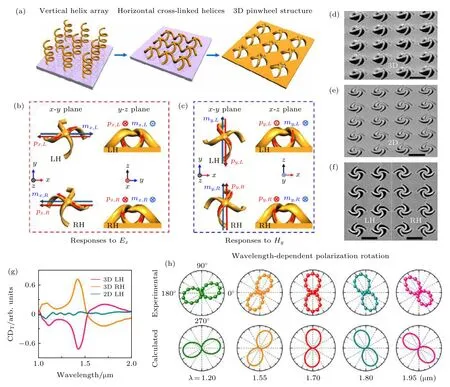
图14 “闭环”纳米剪纸光学超手征特性[43] (a)从螺旋结构到三维风车结构的设计演化示意图; (b), (c) LH 风车结构和 RH 风车结构对入射光电场分量Ex和磁场分量Hy响应的示意图; (d), (e)三维风车结构及二维前体SEM图像, 晶格周期为1.45 µm;(f) LH及RH三维风车结构SEM顶视图; (g)二维LH、三维LH和三维RH结构透射的CD谱; (h)不同波长处三维风车结构的线偏振旋转极坐标图Fig.14.Close-loop nano-kirigami with giant optical chirality[43]：(a) Schematic of a vertical helix array, horizontal cross-linked helices and a 3D pinwheel array; (b), (c) illustrations of the response to the electric field (Ex) and magnetic field (Hy) of incident light for the left-handed (LH) and right-handed (RH) twisted pinwheels, respectively; (d), (e) SEM images of LH pinwheel arrays(e) before and (d) after global FIB irradiation; lattice period：1.45 µm; (f) SEM images of the LH and RH pinwheel structure;(g) measured CD in transmission versus wavelength for 2D LH, 3D LH, and 3D RH pinwheels, respectively; (h) measured and calculated linear polarization rotation angle versus wavelength for 2D and 3D LH pinwheels.

3.2.2 衍射型偏振转换效应

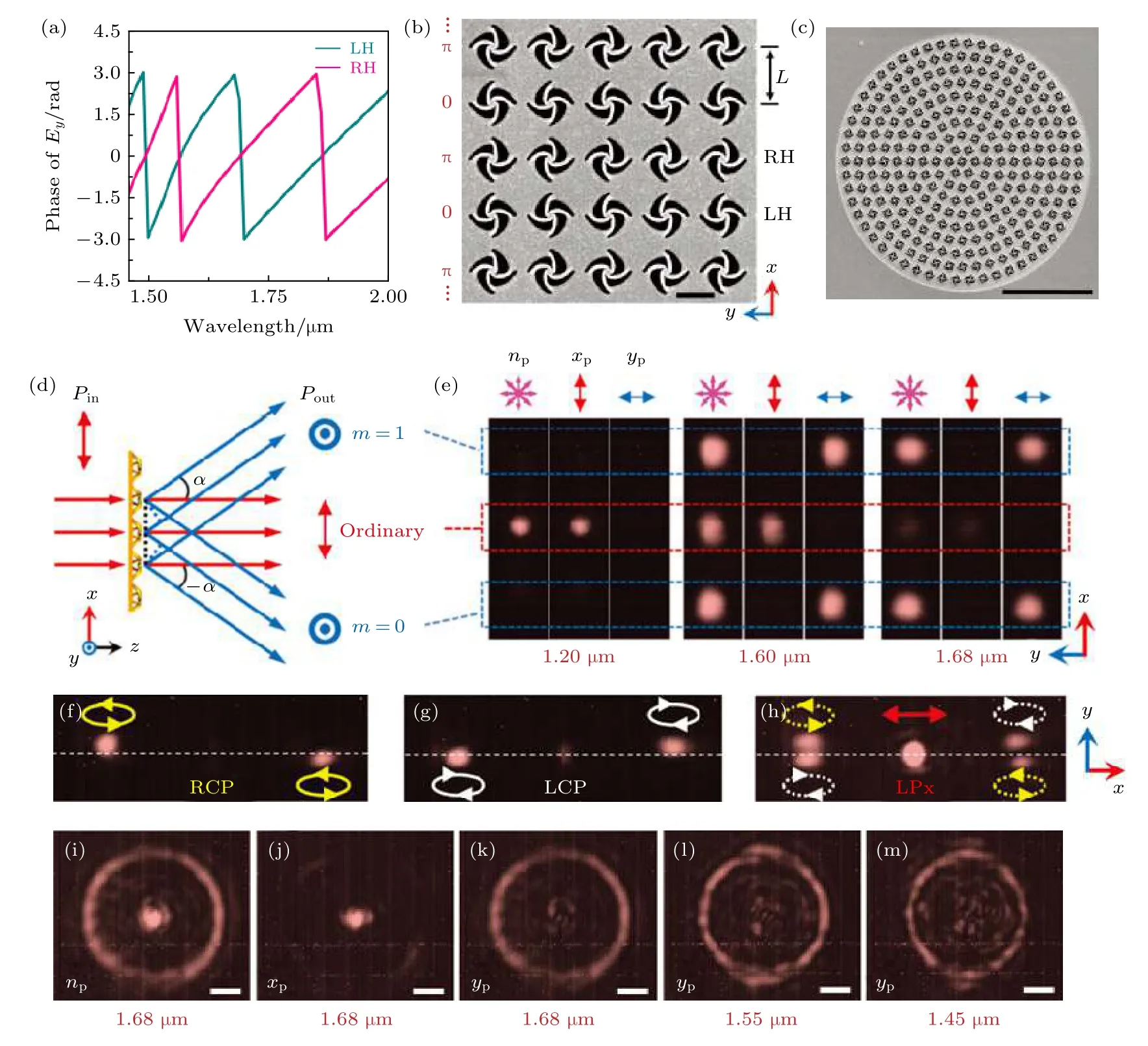
图15 “闭环”纳米剪纸超构表面[66] (a)不同手性结构交叉偏振透射相位光谱; (b)由不同手性风车结构交替排列组成的二元线性光栅 (比例尺：1 µm); (c)由不同手性风车结构交替排列组成的圆形二元光栅的 SEM 图 (比例尺：10 µm); (d) 线性二元光栅对透射光偏振调制示意图; (e)不同波长和探测偏振下二元线性光栅透射实验照片, 入射光为x偏振; (f)-(h)二元线性光栅对圆偏振光的调制; (i)-(m)不同波长和探测偏振下的圆形二元光栅的实验照片(比例尺：10 µm)Fig.15.Metasurface by “closed-loop” nano-kirigami[66]：(a) Transmission phase spectra of Ey for LH and RH pinwheels, respectively;(b) top-view SEM image of a linear grating in which the LH and RH pinwheels are fabricated alternately along the x-direction; scale bar, 1 µm; (c) top-view SEM image of a circular grating; scale bar, 10 µm; (d) schematic of the diffraction properties of the linear grating; (e) CCD camera images of the transmitted light spots at different wavelengths under detection with no polarization (np),x-polarization (xp), and y-polarization (yp), respectively; (f)-(h) CCD images of the spots of the diffracted (left) RCP and (middle)LCP beams under the illumination with LCP, RCP and x-polarized incident light, respectively; (i)-(m) photographs of circular binary gratings at different wavelengths (Scale bars：10 µm).

研究还发现, 当x方向偏振光入射时, 对于LH和RH三维风车结构, 透射的y方向偏振光具有固定的π相位差(图15(a)), 因此对其进行交替排列就能构建性能优异的超构表面衍射光栅(图15(b))[66].由于风车结构的偏振旋转效应只有在波长大于周期时才适用, 因此衍射光线只有对称的两支, 图15(e)中二元光栅工作的实验照片很好地验证了这些特征[66].例如结构在波长为1.6 µm时具有较强的偏振转换特性,x和y偏振均存在透射, 且测得的y偏振光和沿入射方向径直传播的x偏振光并不重合, 说明发生了衍射效应; 在无偏振旋转的1.2 µm波长处, 只有径直传播的x偏振光, 没有任何衍射的y偏振光; 而在发生90°偏振旋转的1.68 µm波长处, 入射光全部转换为出射的y偏振光, 因此只记录到衍射光斑.在线性二元光栅结构中, 衍射偏振转换效应不仅仅针对于入射线偏振光, 也适用于圆偏振光(如图15(f)—(h)所示)[66].圆偏振光通过交替的不同手性结构时, 所产生的相位差为线偏振偏转角度的两倍[66].值得一提的是, 除了由衍射产生的x方向的位移之外, 衍射光斑在y方向也发生了轻微的位移.当入射光为LCP、接收光为RCP时产生的位移方向, 与RCP入射、LCP出射的情况相反(图15(f)和图15((g)).由于相位调制仅沿着x方向, 而光斑的位移发生在y方向上, 因此这种奇妙的现象非常类似于光子的自旋-轨道角动量耦合的PSHE[77-79].其背后的物理机理是, 沿x方向剧烈的相位变化破坏界面的轴对称性, 使得衍射光沿着一条弯折的轨迹传输[66],为了满足角动量守恒, 其偏折的方向会随着入射光手性而发生变化.因此, LCP→RCP和RCP→LCP的自旋-轨道角动量耦合使得圆偏光在垂直于相位梯度方向的传输路径发生改变, 从而引起相反手性的光在y方向上出现相反的位移, 如图15(f)—(h)所示[79,80].

上文中所提及的三维风车结构, 是由具有C4对称性的元胞排列而成, 所以当沿z方向的光线垂直入射时, 结构会引起具有单轴特性的偏振和相位发生变化.因此, 左手和右手风车结构的分布可以灵活配置.如果把左旋结构和右旋结构沿径向交替排列, 还可以构建出径向二元光栅(图15(c)、图15(i)—(m))[66].这种偏振和相位特性可以引入到偏振不敏感的超表面的设计之中.由此可见, 纳米剪纸三维形变为操控光的振幅、相位、偏振、手性等特性提供了一种新的技术途径.

4 结论和展望

综上所述, 纳米尺度的剪纸和折纸技术能够实现丰富的三维功能结构, 正发展成为一门新兴的研究领域.我们从传统剪纸工艺出发, 介绍和总结了一种基于纳米剪纸的三维微纳制造技术.这种技术采用高剂量的FIB作为“剪裁”手段, 低剂量的离子束扫描作为“形变”手段, 实现了丰富的三维结构变换; 采用双层应力分布模型, 精准地预测了FIB辐照下结构的变形过程; 按照离子束辐照方式的不同, 将纳米剪纸归纳为局域扫描和全局扫描制备方式; 根据二维平面图案的拓扑形貌不同, 将以往基于FIB的连续折叠/弯曲的研究总结为“树型”纳米剪纸, 将近期基于拓扑形貌引导的三维纳米结构形变归纳为“闭环”纳米剪纸, 并对各类型的工艺特性和优缺点进行了分析对比.进一步使用多种类型的纳米剪纸方法制造了多功能、前所未见的三维纳米几何结构.最后, 对这些纳米剪纸结构的光子学应用进行了介绍, 包括多重Fano共振及其强耦合作用, 超光学手性, 超构表面衍射、相位和偏振特性, 以及类光子自旋霍尔效应效应等.

通过这些初步的介绍和总结可以发现, 基于FIB的三维纳米剪纸技术具有如下特点：1)其加工的对象需要是悬空的薄膜材料, 无需衬底支撑,目前测试成功的材料广泛, 包括金、银、铝、硅、氮化硅等(对于非导电薄膜, 需要预涂敷或加镀一层超薄的导电材料), 厚度在 50—100 nm, 如商用的各类薄膜窗口 (Norcada, film window); 2)纳米剪纸结构的最小特征尺寸由FIB系统的加工精度决定, 并考虑到三维形变的稳定性, 其最小精度为50 nm; 3)纳米剪纸图案的拓扑构型对结构的三维形变起到了至关重要的作用, “闭环”构型能够产生比“树型”结构更为丰富的三维几何结构, 拓扑形貌与三维形变对应的物理演化模型还有待进一步探索.

与此同时, 基于FIB的三维纳米剪纸技术也存在一些技术挑战：1)当前工艺不适用于非悬空薄膜材料, 如较厚的薄膜或者与较厚衬底结合的薄膜; 2)其制备的样品高度由二维前体的图案决定,在高度方向上扩展的空间有限; 3)基于FIB的纳米剪纸需要样品具有一定的导电性, 加工速度较慢;4)纳米剪纸三维形变的演化与设计亟待建立有效的理论模型.针对这些挑战, 研究团队正在非悬空薄膜材料(如商用氧化硅衬底)、大面积快速加工(如电子束曝光、紫外曝光工艺)等方面开展突破性研究, 并基于三维纳米剪纸结构特征, 开展新型纳米光子器件的应用探索.

总之, 纳米剪纸技术可以使二维平面图案通过形变、原位构建三维立体结构, 从而克服传统自上而下、自下而上、自组装等方法在几何形貌等方面的局限, 为三维微纳加工提供一种新的概念和思路, 可望用来制备新奇的三维纳米几何结构, 在纳米光子学、光力学、微纳机电系统等领域具有重要的应用潜能.例如, 纳米剪纸包含从二维平面到三维立体结构的物理形变, 本质上具有可逆的结构特点, 其悬空的三维结构具有天然的可调谐特性, 有望为光学传感、力学传感、生物医学传感、动态光学显示、柔性材料转移等领域带来一些新的应用机制.

感谢华南理工大学李志远教授, 美国麻省理工学院方绚莱教授和杜汇丰博士, 中国科学院物理研究所微加工实验室的刘哲博士、李无瑕副研究员、李俊杰研究员、顾长志研究员、杨海方研究员、金爱子和全保刚副主任工程师, 中国科学院物理研究所光物理实验室的陆凌研究员、刘荣鹃副研究员、田喜敏博士、张东香研究员、冯宝华研究员和张秋琳高级工程师, 北京理工大学物理学院王荣瑶教授、张向东教授、姚裕贵教授等的支持与合作.