多格点相互作用对横向磁场作用下XY型自旋链中非平衡态热力学性质的影响*

贺志 余敏 王琼

1) (洞庭湖生态经济区建设与发展湖南省协同创新中心, 常德 415000)

2) (湖南文理学院数理学院, 常德 415000)

近年来, 封闭系统中非平衡热力学性质, 特别是自旋链中经过一个淬火过程后的平衡热力学性质已经成为了量子热力学研究中的一个热点之一.研究了横向磁场作用下含XZX+YZY型三体相互作用的XY自旋链中的非平衡态热力学性质.具体考虑了当XY型链中横向外磁场发生一个突变(淬火)时链中XZX+YZY三格点相互作用分别对淬火过程中产生的平均功、功涨落和不可逆熵产生等热力学量的影响.研究显示：XZX+YZY三格点相互作用可能对平均功的增加起正面作用和负面作用, 关键取决于初始外磁场强度的取值.接着, 还发现：通过调节XZX+YZY三格点相互作用强度可以很有效地抑制功涨落.最后, 考虑了不可逆熵产生在不同XZX+YZY三格点相互作用下随外磁场强度的变化关系, 结果发现：不可逆熵产生在临界磁场附近会出现特殊的尖峰特征, 并且尖峰值随XZX+YZY三格点相互作用的增加有不断减少的趋势, 同时给出了相应的物理解释.

1 引 言

随着基于超冷原子体系[1-3]的实验研究取得了一系列的重要进展, 人们重新对封闭系统中非平衡热力学的研究产生了浓厚的兴趣.特别地, 一些普适的量子涨落关系如Jarzynski等式[4]、Tasaki-Crooks关系[5,6]的提出, 极大地促进了非平衡热力学在理论[7-11]和实验[12-16]上的发展.而利用突然改变系统参数(淬火)手段, 是实现非平衡过程的一种重要方式.近年来, 研究量子多体系统如自旋链中经过一个淬火过程后的非平衡热力学性质迅速成为了一个热点课题.Silva[17]研究了横向伊辛模型中发生一个淬火过程时功的统计性质, 发现了功分布会在临界磁场表现奇异性.Dorner等[18]研究了横向伊辛模型中包括平均功和不可逆熵产生等量子热力学量, 并给出了热力学量的精确表达式.Bayocboc和Paraan[19]研究了一般XY型自旋链模型中功分布涨落以及不可逆熵产生等量子热力学量在不同各向异性参数下随外磁场变化关系.Zhong和Tong[20]研究了XZY—YZX三格点相互作用对XY型自旋链模型中平均功和不可逆熵产生等量子热力学量的影响.Wang等[21]研究了Dzyaloshinsky-Moriya (DM)相互作用对 XY型自旋链模型中平均功、功涨落以及不可逆熵产生等的影响.Xu等[22]研究了量子相干性对功的统计性质的影响.我们注意到, 自旋链系统中除了平时考虑的近邻两格点相互作用外, 可能还存在XZY—YZX型和 XZX+YZY 型三格点相互作用.Roger等[23]研究发现了三格点相互作用能用来描述固态3He的磁性机制.Titvinidze和Japaridze[24]研究了XZX+YZY型三格点相互作用对推广的XY自旋链模型中相图的影响.Cheng和 Liu[25,26]分别研究了XZY—YZX三格点相互作用对两量子比特与各自XY自旋链相互作用模型中的量子纠缠, 以及XZX+YZY型三格点相互作用对 XY自旋链模型中量子相变的影响.Lian[27]研究了XZX+YZY三格点相互作用对一个量子比特系统与 XY自旋链耦合模型中 Loschmidt echo (LE)演化的影响.Shan[28]研究了XZX+YZY三格点相互作用对XY自旋链系统中的几何相位与量子相变的影响.郗玉兴等[29]研究了 XZX+YZY和XZY—YZX 三格点相互作用对XXZ自旋链模型中隐形传态量子的影响.

从以上研究的结果看, 虽然XZY—YZX三格点相互作用[20]和DM相互作用[21]在一个淬火过程中的非平衡量子热力学性质的影响已经分别被人们研究.但到目前为止, 还未见到关于XZX+YZY三格点相互作用对于一个淬火的XY自旋链模型中非平衡量子热力学的影响的研究报道.另外, 据我们所知：XZY—YZX三格点相互作用[20]和DM相互作用[21]在XY自旋链模型中所起的作用只体现在能谱中, 它们同由波戈留波夫变换决定的本征态是无关的.然而, XZX+YZY型三格点相互作用在XY旋链模型中的作用不仅体现在能谱中, 也同由波戈留波夫变换决定的本征态密切相关[26-28].它们之间的这个显著区别是促使本文研究的主要初衷之一.因此, 本文研究了 XZX +YZY三格点相互作用对于一个淬火的XY自旋链模型中平均功、功涨落和不可逆熵产生等量子热力学量的影响.研究发现：XZX+YZY三格点相互作用可能对 XY自旋链淬火过程中平均功的增加起正面作用和负面作用, 关键取决于初始外磁场强度的取值.另外也发现：通过调节 XZX + YZY 三格点相互作用强度可以很有效地抑制淬火过程中的功涨落.总之, 本文获得的结果对进一步研究淬火过程中的非平衡态热力学有一定的借鉴意义.本文结构安排如下：在第2节简要介绍了非平衡态热力学中的一些重要物理量, 如功分布、平均功、功涨落、不可逆熵产生等的定义; 在第3节中给出了研究的理论模型及其精确解; 第4节是数值模拟结果的理论分析和讨论; 第5节对文中获得的结果做了简要总结和展望.

2 非平衡态热力学：平均功、功涨落和不可逆熵产生

本节简要地介绍在非平衡态热力学中一些重要的概念和公式, 如平均功、功涨落、不可逆熵产生等.这里考虑一个量子系统的动力学, 它由一个含有外界控制参数(或者叫功参数)λ(t) 的哈密顿量H(λ(t)) 来决定.假设对于一个固定的功参数λ(t≤ 0)=λ0, 系统最初与一个热库 (温度为β=1/T)被制备在一个热平衡态, 即系统的初态就可以用吉布斯热平衡态来表示为

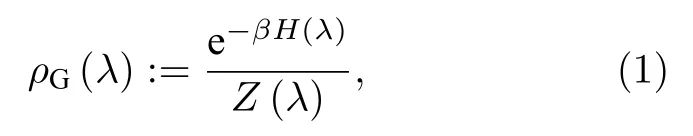
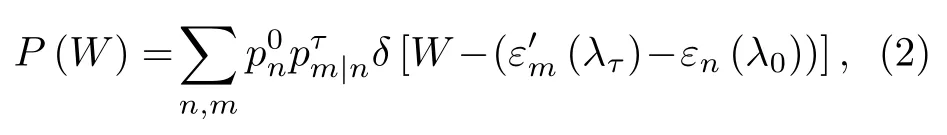
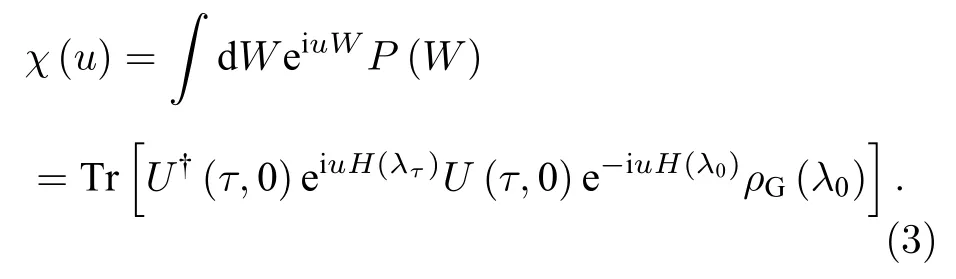
一方面, 由功的第n阶量的平均计算公式以及累积量的定义可知：平均功及功的方差 (也被称为功涨落)Σ2=能表示成

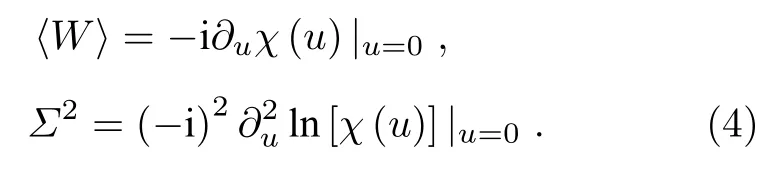
另一方面, 方程(2)中功分布的量子统计本质允许我们将热力学第二定律重新改写为其中 ∆F表示系统自由能的增量.如果要将这个不等式写成等式, 则和 ∆F之间存在这样的关系：被称为平均不可逆功.这样可以得到平均不可逆功∆F.进一步, 所谓的不可逆熵产生 ∆Sirr被定义为[4]

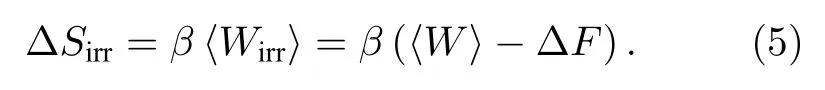
特别地, 不可逆熵产生 ∆Sirr是非平衡态过程中不可逆性的一个度量方式.值得指出的是, 不可逆熵产生 ∆Sirr也可等价地用一个给定时刻的密度算符与一个假设的吉布斯热平衡态之间的量子相对熵来表示[30]：

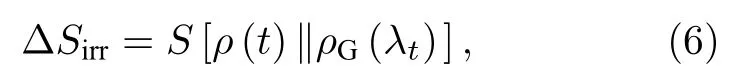
其中S(ρ||ρ∗)=Tr(ρlogρ-ρlogρ∗)表示任意两个态ρ和ρ∗之间的相对熵.特别地, 文献 [18, 30, 31]研究表明：当系统的哈密顿量在外界因素作用下经历一个突然改变(淬火)时, 这个淬火过程中产生的不可逆熵产生 ∆Sirr能表示成淬火之前和淬火之后对应的吉布斯热平衡态之间的距离：

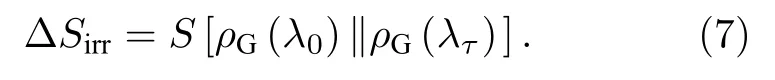
3 理论模型及其精确解

本文将考虑一个一维带有XZX + YZY三格点相互作用的各向异性XY自旋链系统模型.该模型对应的哈密顿量可表示成[24,26-28]

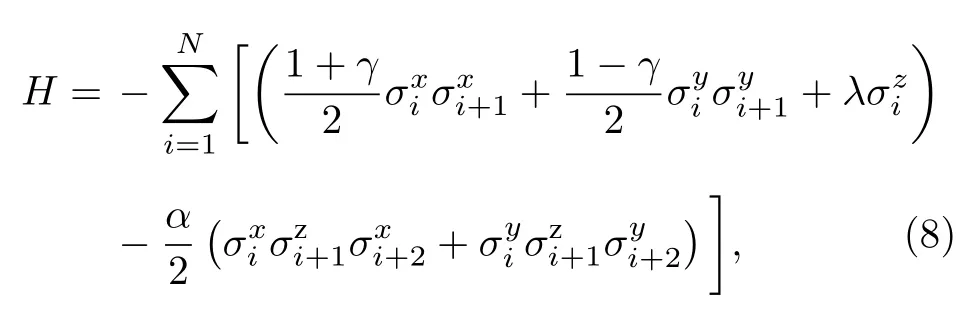
其中参数N表示整个自旋链的格点数, 参数表示著名的3个泡利矩阵, 参数γ表示在XY平面中任意两个自旋粒子之间相互作用的各向异性参数, 参数λ表示施加在每个自旋粒子上的横向磁场强度, 以及α表示 XZX+YZY 型三格点相互作用强度.在 XY自旋链系统模型中三格点相互作用可形象用图1来表示.原则上, 可以研究当方程 (8)中γ,λ,α三个参数中任意一个参数发生一个突变时的非平衡态热力学性质.然而, 考虑到施加在自旋粒子上的横向外磁场比较容易操控.所以, 本文仅讨论当横向外磁场发生一个突变时方程(8)所示模型中的非平衡态热力学性质.

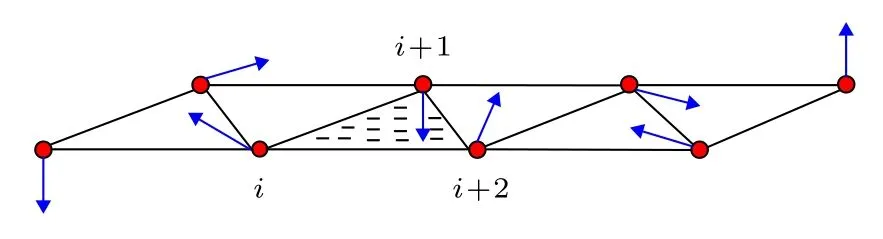
图1 带有 XZX+ YZY 三格点相互作用的 XY 自旋链系统模型的示意图[24]Fig.1.Schematic representation of the structure of the XY model with XZX + YZY three site interaction[24].

方程(8)所示的哈密顿量可通过著名的Jordan-Wigner变换、傅里叶变换和波戈留波夫变换被对角化[26-28,32].首先通过 Jordan-Wigner变换可以将自旋粒子映射为一维无自旋费米子, 它们之间的算符关系通过如下方式联系：

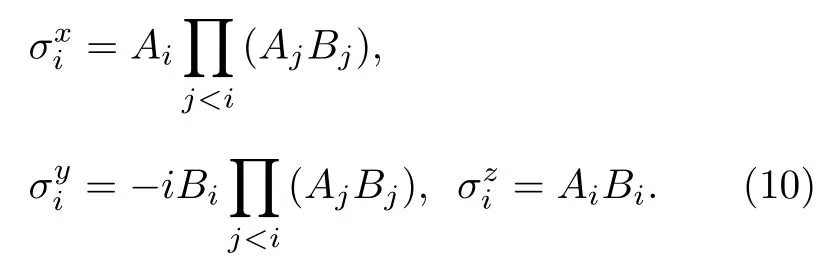
这样, 方程(8)中的哈密顿量被转换成

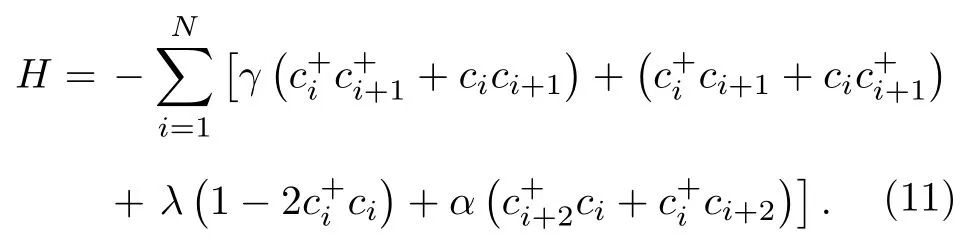
接下来, 对方程(11)右边按顺序分别做傅里叶 变 换 如以 及 波 戈留波夫变换如νk=sin(θk/2))后, 方程(5)中的哈密顿量能化成对角化的形式

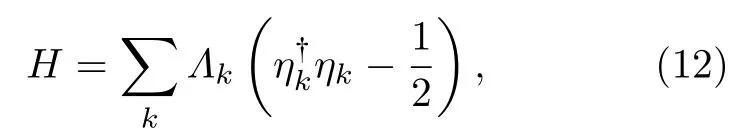
其中能谱

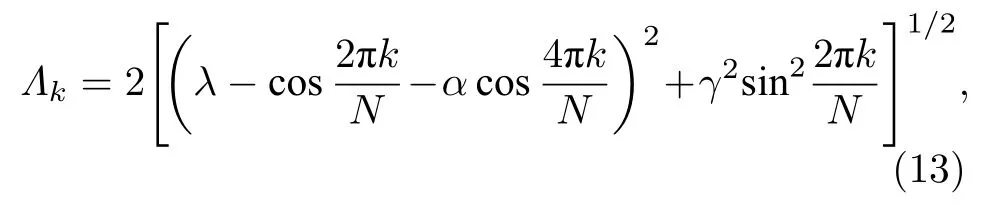
并且

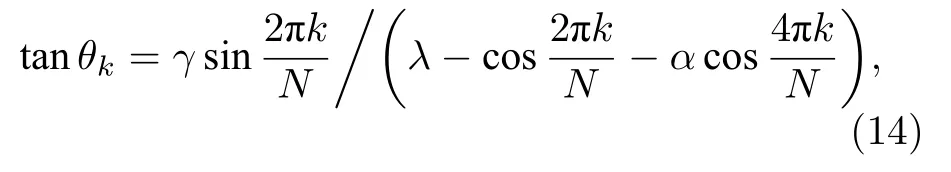
且对于一个偶数N,k=-(N-1)/2,···, (N-1)/2 .明显地, 当考虑α=0 , 能谱

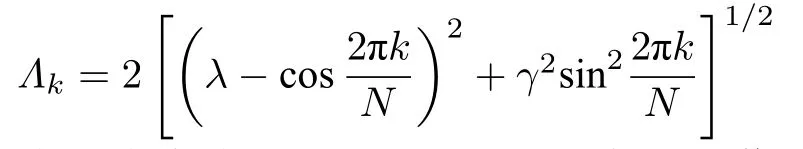
退化成没有考虑 XZX+YZY 三格点相互作用的XY型自旋链的能谱[18,33,34].

本文考虑一个淬火过程, 即在XY型自旋链中, 通过外界的控制给自旋粒子的磁场从开始t=0时的λ0经过一个极小的时间τ突然改变到λτ的过程.假设自旋链系统最初处在吉布斯热平衡态如方程(1)所示, 那么不难得到对应的配分函数Z(λ0)有

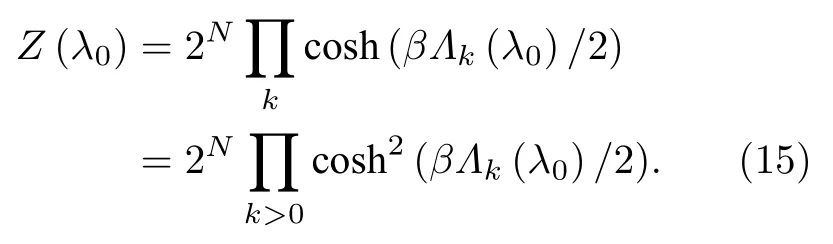
采用类似于上面的对角化程序, 那么在τ时刻自旋链系统的哈密顿量有对角化形式明显地, 在时刻τ的费米算符和在开始t=0 的费米算符是不相同的, 然而它们之间关系可通过下列方式得到.首先考虑到波戈留波夫变换

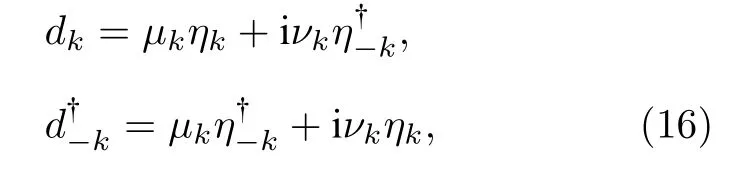
式中µk=cos(θk/2),νk=sin(θk/2)), 可得到

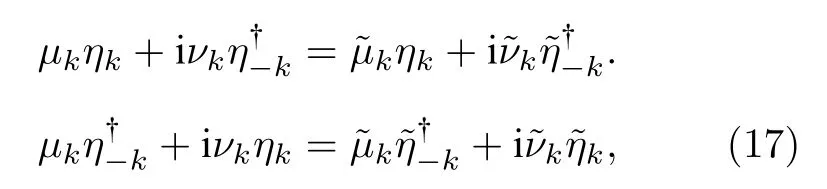
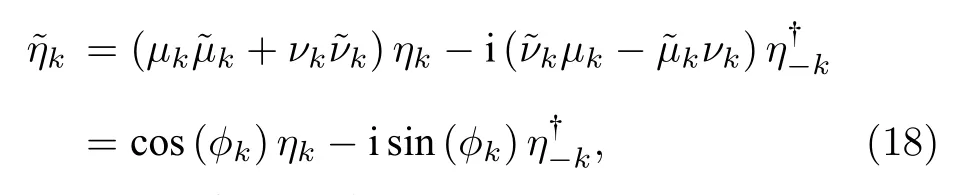
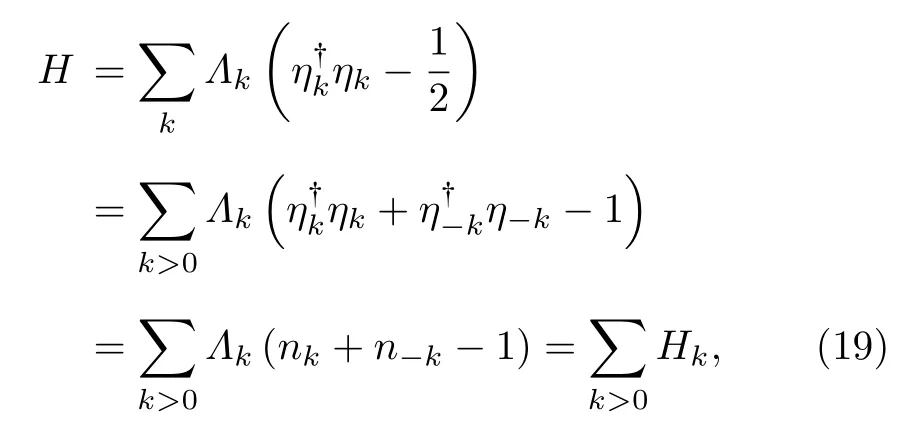
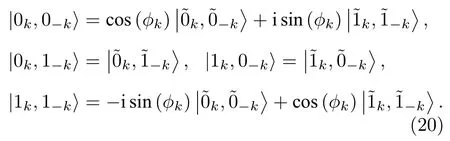
由于本文考虑的是系统的哈密顿量经历一个淬火过程(意味着系统还来不及演化), 所以自旋链系统自身演化的幺正算符U(τ,0) 为一个单位算符, 这样功分布的特征函数如方程(3)能简化为

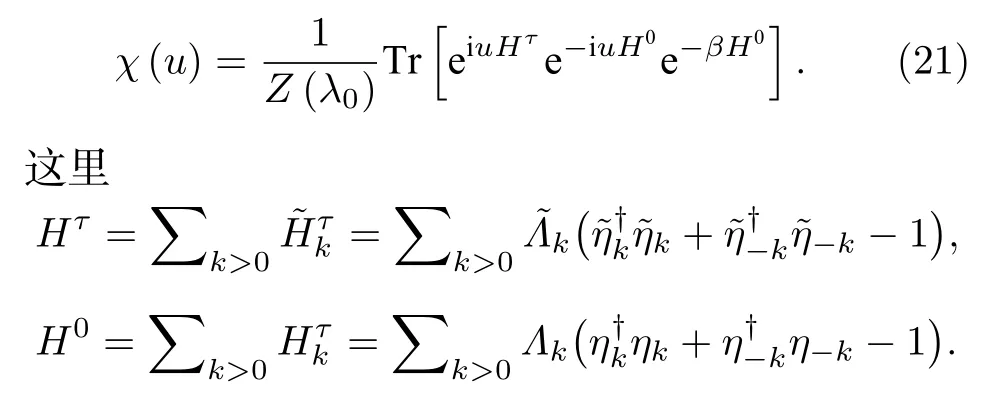
利用方程(20), 方程(21)所示功分布的特征函数能够被获得：

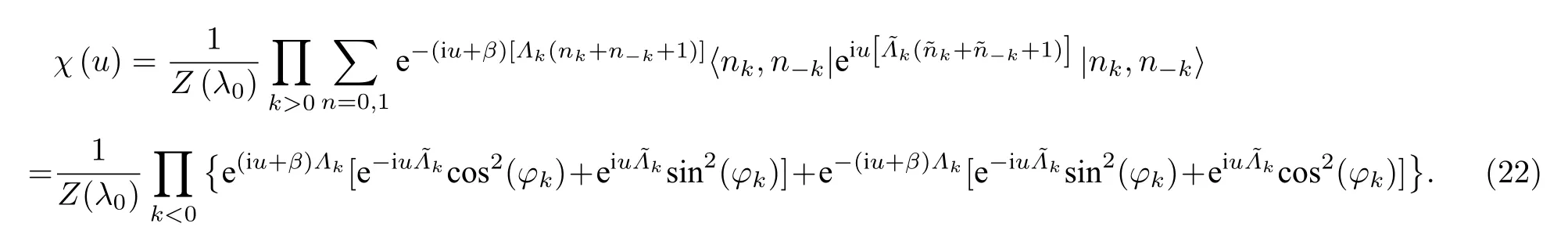
根据已有对于研究量子伊辛模型[18]和XY型自旋链模型[19,20]的研究结果可知, 一旦功分布的特征函数的表达式已知, 不难证明著名的Jarazynski等式[4]以及Tasaki-Crooks关系[5,6]都是成立的.只是本文考虑的模型与他们研究的模型稍有不同,而实际的证明过程是相同的, 这里为了避免重复,证明过程在此省略.

进一步, 根据方程(4)中平均功及功涨落的定义, 本文考虑的模型中的平均功⟩和功涨落Σ2能被获得精确的表达式：

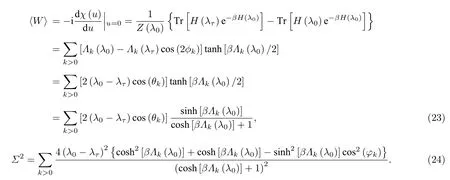
又根据著名的Jarazynski等式[4]

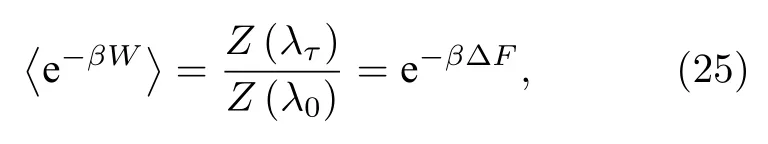
能获得

这样不可逆熵产生如方程(5)能退化成

4 分析与讨论

4.1 XZX+YZY三格点相互作用对平均功及功涨落Σ2的影响

相互作 用 强度 (α=0.0,0.2,0.6) , 平均功随初始外磁场强度λ0的改变呈现单调递减到一个共同的稳定值的变化关系, 如此类似的关系也存在于其他自旋链模型如带有DM相互作用XY自旋链中[21].2) 这里存在一个临界的初始外磁场强度λ0c, 当λ0＞λ0c时, XZX+YZY三格点相互作用对平均功的增加起着一个正面的作用, 即随着XZX+YZY三格点相互作用强度α的增加, 平均功也单调地增加; 而当λ0＜λ0c时, XZX+YZY三格点相互作用对平均功的增加起着一个负面的作用, 即随着三格点相互作用强度α的增加,平均功会单调地减少.为了更细致地阐明上述关系, 在图2(a)的内插图中分别给出了对于不同的λ0值(如λ0=0.5,1)平均功随三格点相互作用强度α的变化.明显地, 当选择λ0=0.5 时, 平均功随α的增加而单调地减少(见图2(a)内插图中的实线); 当选择λ0=1 时, 平均功⟩随α的增加而单调地增加(见图2(a)内插图中的虚线).总之, 图2(a)的内插图中曲线的变化趋势同前面所得到的结果是完全符合的.我们注意到, 这一结果不同于文献[21]研究的带有DM相互作用XY自旋链中DM相互作用对平均功的影响.在文献[21]中, Wang等发现：在初始外磁场强度λ0c所取范围内(同本文中所取范围是相同的), DM相互作用对平均功的增加总是起着一个正面的作用, 即在0≤λ0≤2范围内, 随着DM相互作用强度的增加,平均功也单调地增加.之所以本文考虑的XZX+YZY三格点相互作用同DM相互作用对相同 XY型自旋链模型中平均功的影响有区别是因为：DM相互作用产生的效果只体现在能谱中[21],而相应能量本征态与DM相互作用是无关的.而本文考虑的 XZX+YZY 三格点相互作用产生的效果不仅体现在如方程(13)的能谱中, 而且也体现在相应的能量本征态(14)中.另外, 图2(b)也显示了类似的变化规律.因此, 在本文考虑的模型中,XZX + YZY三格点相互作用对平均功是起正面作用还是负面作用, 与初始外磁场强度λ0的取值密切相关.3) 随着各向异性参数γ越大, 三格点相互作用强度α对平均功的影响就越小(比较图2(a)和图2(b)).

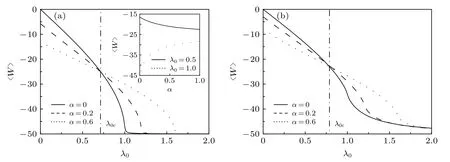
图2 平均功 在不同的三格点相互作用强度 α 和各向异性参数 γ 下随初始外磁场强度 λ0 的变化 (a) γ =0.1 ; (b) γ =0.8 ;其他的参数被设定为 β =100 , δ λ= λτ-λ0=0.01 ,N=5000Fig.2.Averaged work 〉 and work distribution fluctuation Σ 2 as a function of λ0 under various α for γ =0.1 (a) and γ=0.8(b).Other parameters are β =100 , δλ = λτ-λ0=0.01 and N =5000 .

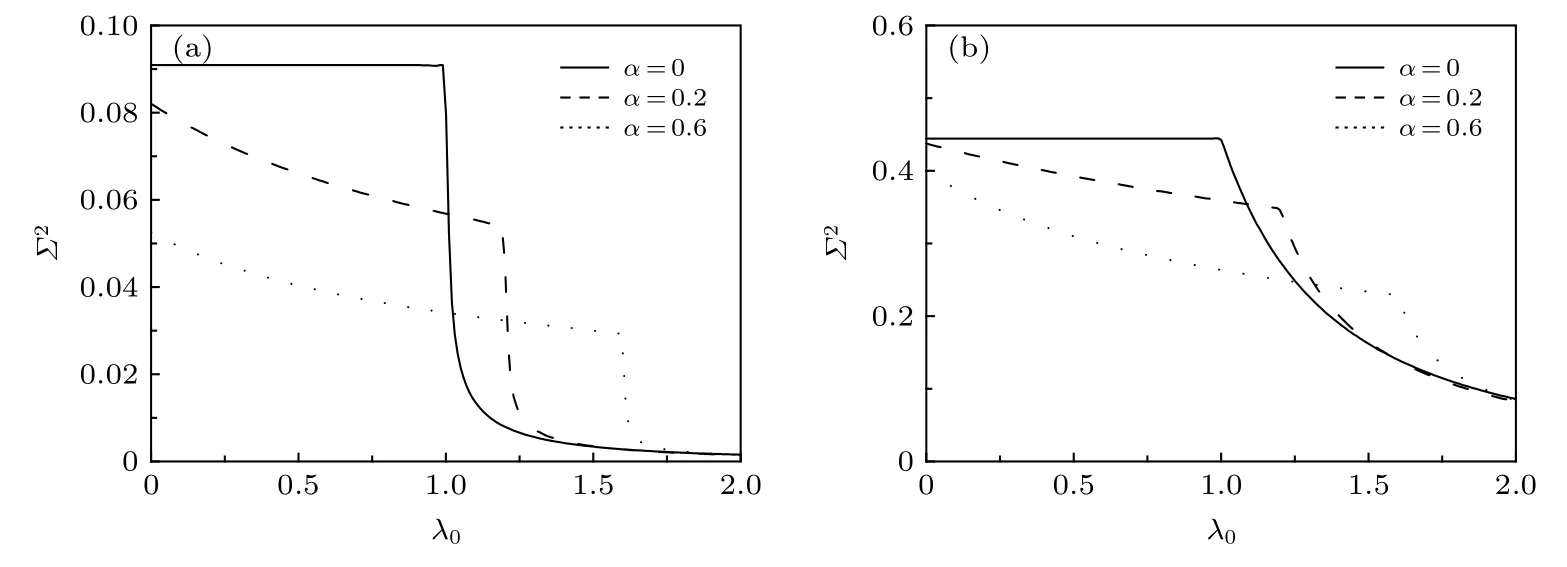
图3 功涨落 Σ 2 对于不同的三格点相互作用强度 α 和各向异性参数 γ 随初始外磁场强度 λ0 的变化 (a) γ =0.1 ; (b) γ =0.8 ;其他的参数被设定为 β =100 , δλ = λτ-λ0=0.01 ,N=5000Fig.3.Work fluctuation Σ 2 as a function of λ0 under various α for γ =0.1 (a) and γ =0.8 (b).Other parameters are β=100,δλ= λτ-λ0=0.01and N =5000 .

接下来, 进一步研究 XZX+YZY三格点相互作用强度α和各向异性参数γ对功涨落Σ2的影响.具体给出了功涨落Σ2对于不同的XZX+YZY三格点相互作用强度α和各向异性参数γ随初始外磁场强度λ0的变化, 如图3所示.通过观察图3(a)和图3(b), 可以发现一些有兴趣的结果：1)明显地, 通过调节三格点相互作用强度α可以很有效地抑制功涨落Σ2(如短划线与点线).2)当没有考虑XZX+YZY三格点相互作用如α=0 (如实线所示)时, 功涨落Σ2从开始经过一段平缓区域后突然单调衰减.这表示功涨落Σ2对较小的初始外磁场强度λ0是不敏感的, 而对较大的初始外磁场强度λ0比较敏感.而当考虑了三格点相互作用如α=0.2,0.6(如短划线和点线所示)时, 功涨落Σ2从一开始呈现下降到突然单调衰减.这说明XZX +YZY三格点相互作用可以提高功涨落Σ2对初始外磁场强度的敏感度, 从而达到抑制功涨落的目的.3) 有没有考虑XZX+YZY 三格点相互作用其功涨落Σ2出现明显衰减的临界磁场位置是不同的,如没有考虑XZX+YZY三格点相互作用α=0 ,临界磁场强度在λ=λc=1 (如实线所示); 而当考虑 XZX+YZY 三格点相互作用时功分布涨落Σ2的临界磁场强度是λ=λc=1+α(如短划线和点线所示).我们注意到, 这些临界磁场强度是同用著名 Loschmidt echo (LE)的动力学敏感性来判定伊辛自旋链模[35]、标准的各向 XY 自旋链模型[36]、含有 XZX+YZY三格点相互作用的 XY自旋链模型[24,27]中量子相变发生的临界磁场位置是相同的,其原因是文中方程(3)所示的特征函数同LE有类似的形式[37].其实, 在图2即平均功随初始外磁场强度λ0c变化曲线中也有相同临界磁场位置,只是没有这么明显.4) 随着各向异性参数γ的增加, 功涨落Σ2随初始外磁场强度λ0变化的趋势都将变得更为平缓.

4.2 XZX+YZY三格点相互作用对不可逆熵产生 ∆Sirr的影响

最后来研究XZX+YZY三格点相互作用对量子热力学中一个很重要的物理量即不可逆熵产生∆Sirr的影响.根据方程(27), 给出了不可逆熵产生∆Sirr对于不同的 XZX+YZY 三格点相互作用强度α随初始外磁场强度λ0的变化, 结果如图4所示.其中图4(a)对应较小的各向异性参数γ=0.1的情况; 而图4(b)对应较大的各向异性参数γ=0.8 的情况.从图4(a)和图4(b)可以看到, 在低温下 (β=100) , 对于 各种三格点相互 作用强度(α=0→0.2→0.6), 不可逆熵产生 ∆Sirr在临界磁场强度附近都存在一个尖峰现象, 这个尖峰的出现能够利用一个给定时刻的密度算符与一个假设的吉布斯热平衡态之间的量子相对熵来解释.从方程(6)可知, 不可逆熵产生 ∆Sirr等价于一个给定时刻的密度算符与一个假设的吉布斯热平衡态之间的量子相对熵.特别地, 对于系统的哈密顿量经过一个淬火过程使得哈密顿量中的参数发生一个突变时, 不可逆熵产生 ∆Sirr进一步简化成淬火之前和淬火之后对应的吉布斯热平衡态之间的距离,如 方 程 (7), 即 ∆Sirr=S[ρG(λ0)||ρG(λτ)] .那 么 ,当外界横向磁场强度在其临界磁场强度附近发生一个很小的改变时, 相应的热平衡态之间将会发生一个显著的改变, 这样导致不可逆熵产生 ∆Sirr在外界磁场强度接近临界磁场强度时表现为急剧增加或减少而形成尖峰特征.进一步还发现, 随着XZX+YZY三格点相互作用α的增加(如图4中的实线 → 短划线 → 点线), 不可逆熵产生 ∆Sirr出现尖峰位置不断地降低.这个结果能被解释如下：没有XZX+YZY 三格点相互作用时的临界磁场强度是在λ=λc=1 , 而有 XZX+YZY 三格点相互作用时临界磁场强度是在λ=λc=1+α.假设外磁场强度偏离临界磁场强度一个小量ε, 那么, 没有XZX+YZY 三格点相互作用时其淬火前的外磁场强 度 为λ0=1-ε, 淬火后的外磁场强度为λτ=0.01+λ0=0.01+1-ε; 而有 XZX+YZY 三格点相互作用时其淬火前的外磁场强度为λ0=α+1-ε, 淬火后的外界磁场强度为λτ=α+0.01+1-ε.通过简单的数值计算发现,不可逆熵产生 ∆Sirr如方 程 (27)随着 XZX +YZY三格点相互作用强度α的增加而不断地减少.这样导致了不可逆熵产生 ∆Sirr的尖峰位置随三格点相互作用α的增加不断地降低的特征.最后, 比较图4(a)和图4(b), 明显可看出, 随着各向异性参数γ的增加, 不可逆熵产生 ∆Sirr随初始外磁场强度λ0呈现更平缓的变化趋势.

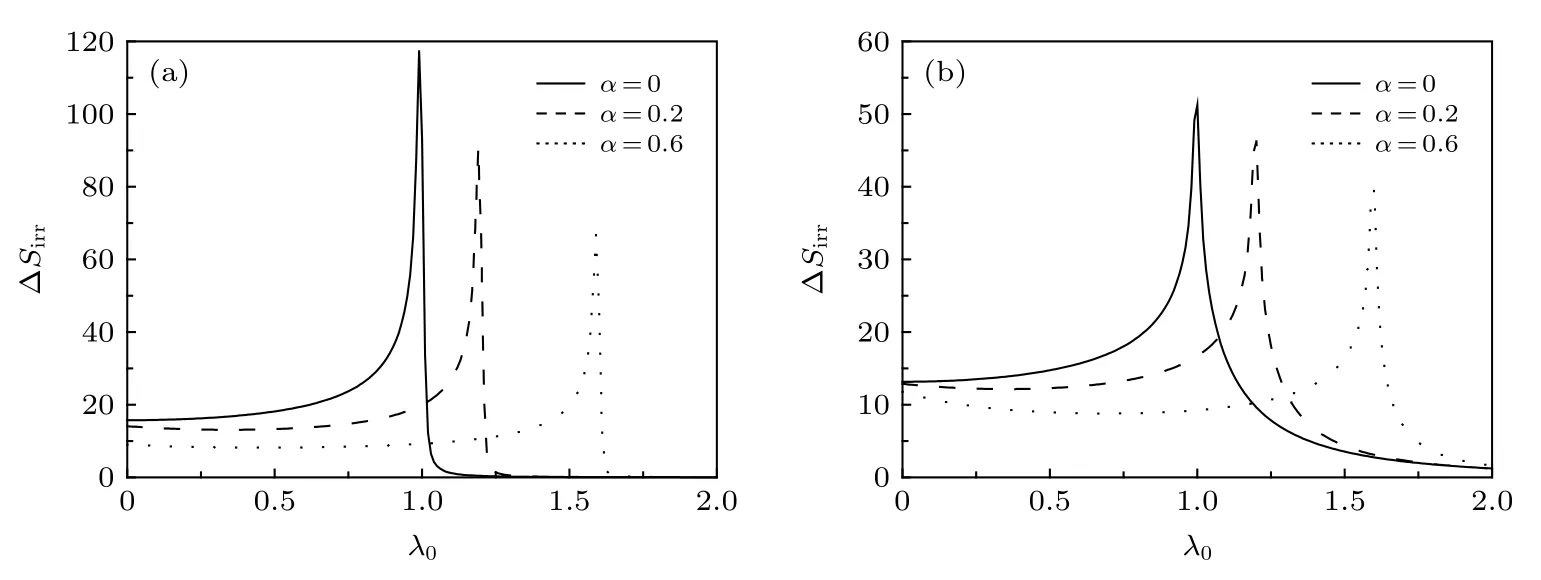
图4 不可逆熵产生 Δ Sirr 对于不同的三格点相互作用强度 α 和各向异性参数 γ 随初始外磁场强度 λ0 的变化 (a) γ =0.1 ;(b) γ =0.8 ; 其他的参数被设定为 β =100 , δλ =λτ-λ0=0.01 ,N=5000Fig.4.Irreversible entropy production Δ Sirr as a function of λ0 under various α for γ =0.1 (a) and γ =0.8 (b).Other parameters are β =100 , δλ = λτ-λ0=0.01 and N =5000 .

5 结 论

考虑了XZX+YZY三格点相互作用对XY自旋链中当横向磁场发生一个突然改变时的平均功、功涨落、不可逆熵产生等量子热力学量的影响.通过解析求解和数值模拟, 发现了一些很有兴趣的结果.1) XZX+YZY三格点相互作用可能对平均功的增加起正面作用和负面作用, 与初始外磁场强度λ0的取值密切相关.2) 通过调节 XZX+YZY 三格点相互作用强度可以很有效地抑制功涨落.这一结论同文献[21]对于DM相互作用对XY型自旋链模型中功分布的影响是相同的, 即通过调节DM相互作用强度可以很有效地抑制功涨落.3) 不可逆熵产生在临界磁场附近会出现特殊的尖峰特征,并且尖峰值随XZX+YZY三格点相互作用的增加有不断减少的趋势.进一步, 利用对于一个突然淬火的物理过程, 不可逆熵产生 ∆Sirr能表示成淬火之前和淬火之后对应的吉布斯态之间的距离(方程(7)), 且对不可逆熵产生在临界磁场附近会出现尖峰特征可以进行合理的物理解释.这里需要指出的是, 文中获得的相关结果是在低温条件即β=100的条件下获得的.至于在高温条件, 即β较小下XZX+YZY三格点相互作用对平均功、功涨落以及不可逆熵产生的影响与文中在低温条件给出的结果是否有很大的差别, 这值得今后进一步研究.总之, 本文获得的结果, 将在淬火非平衡量子热力学领域的相关研究中有一定的理论指导意义.